功放预失真中自适应算法研究

韩 冰，晋东立

（北京跟踪与通信技术研究所，北京 100094）

功放预失真中自适应算法研究

韩 冰，晋东立

（北京跟踪与通信技术研究所，北京 100094）

数字基带预失真技术是补偿功放非线性的最有效方法之一，而自适应算法的选择很大程度上影响着系统的预失真性能。其中，最小均方误差（LMS）算法和递归最小二乘法（RLS）是最常用的自适应收敛算法，LMS算法计算复杂度较低，但LMS算法收敛速度慢，易陷入局部最优且精度不高，RLS收敛性能较好，但计算复杂度高。在综合分析2种算法优缺点的基础上，提出了一种LMS和RLS算法的组合算法，仿真结果表明，组合算法的预失真性能很好，而且算法复杂度较低。

功率放大器；数字预失真；LMS；RLS变步长

0 引言

功率放大器是通信系统的重要组成部分，其作用是将射频信号的功率进行放大，以此来满足发射机对发射功率的要求，信号经过功放将会失真，而功放的2个性能指标：要求非线性失真小与功率效率尽可能高，是一对矛盾关系。早期，采用功率回退法以减小非线性失真，但导致了功放效率低。为提高功放的效率，一般使功放工作在非线性区，带来的影响是带内误码率升高以及带外频谱扩展。目前，数字预失真是补偿功放非线性最有效的方法之一，其原理是在功放前加一个与功放特性互逆的预失真器，优点是硬件实现简单、适应性强以及效率高。而且数字信号处理（DSP）技术的发展将会带动数字预失真技术更广泛的应用。

目前，查表法和多项式法是数字预失真常用的2种技术手段［1］。查表法的精度与存储表项的大小直接相关，表项越多，预失真精度越高，但所需的存储空间也越大；多项式预失真自适应能力好，可采用高阶多项式来实现较高的预失真性能。预失真模型建立以后，可以采用直接学习结构和间接学习结构对系统进行辨识，其中采用间接学习结构可以省略对功放参数的辨识，复杂度较低［2，3］。

1 预失真的自适应收敛算法

通信预失真系统如图1所示，模型建立和模型辨识是预失真系统的2个重要组成部分。本文选择Saleh模型［4］作为功放模型，以多项式模型为预失真器模型，其中，Saleh功放模型的输出信号幅度与输入信号幅度之间的关系为：

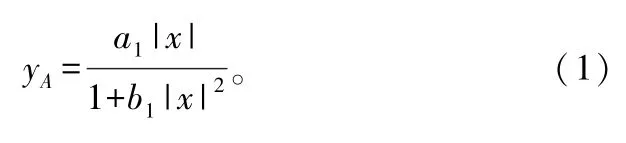
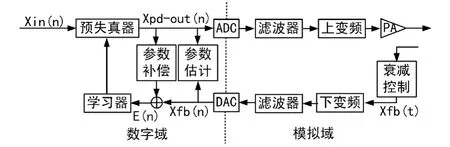
图1 预失真系统结构图

输出信号相位较输入信号相位增加为：

对于无记忆功放模型而言，基于多项式的预失真器模型的数学表达式为［4］：

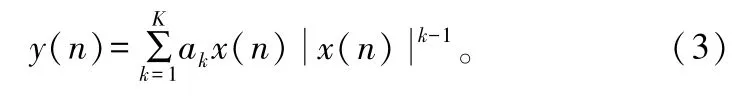
采用间接学习结构对预失真器参数进行辨识，间接学习结构框图如图2所示。

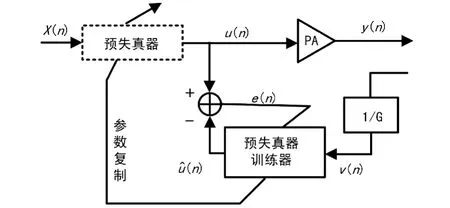
图2 间接学习结构框图

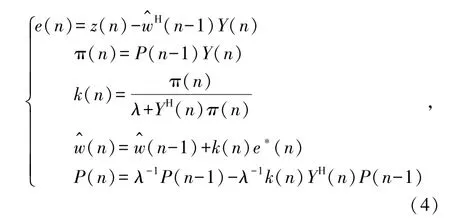
式中，λ为遗忘因子，一般取0＜λ＜1。RLS收敛速度快，收敛性能好，但是计算量大，实现较为复杂。

传统的固定步长的LMS算法的迭代过程为：

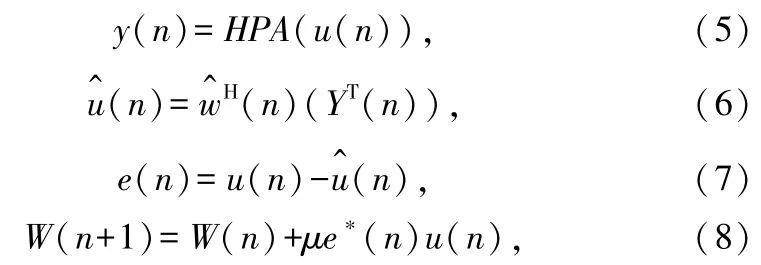
式中，μ是自适应算法中的迭代步长，（·）H表示复共轭转置，（·）∗表示复共轭，W（n）＝［w0（n），w1（n），w2（n），…，wL－1（n）］为n时刻多项式系数的更新权值，μ决定算法的收敛速度和稳定性，μ须满足0＜μ＜1／λmax，λmax＝mnax （E（XT（n）X（n）］）。当步长μ固定时，收敛速度、稳态性能以及跟踪性能不能同时得到满足。而且当步长固定时，易陷入局部最优［8］，因此，目前对LMS算法的研究主要集中在变步长上。

针对LMS算法的研究几种在变步长LMS算法上，变步长算法遵循的一般原则为，当初始阶段误差较大时，步长因子应较大，以加速收敛，当误差较小时，选择较小的补偿因子，保证收敛的稳态。能同时获得较小的稳态误差和较快的收敛速度，基于Sigmiod函数的变步长LMS算法（SVSLMS）的步长因子为：

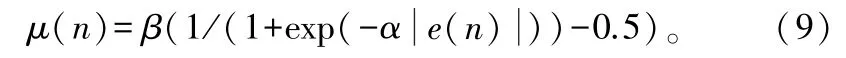
不过此算法在误差e（n）接近0时变化较大，使得SVSLMS算法在自适应稳态阶段仍有较大的步长变化。为解决这个问题，文献［5］在SVSLMS算法的基础上提出的变步长算法（G-SVSLMS）为：

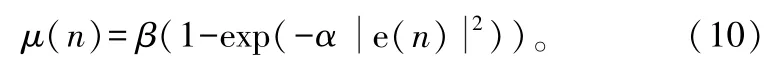
此时，μ（n）在e（n）接近0时，变化缓慢，收敛速度较快，但是此算法仅与当前时刻的误码有关，抗噪能力较差，当信噪比较低时，算法精度容易受到影响。

由于噪声的存在，G-SVSLMS算法不能较好反映自适应状态的迭代过程，于是文献［6］提出如式（11）的改进算法：

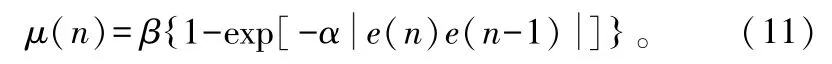
上述LMS类算法的步长因子均与反馈误差有关，还有一类与输入信号有关的变步长LMS算法，归一化LMS（NLMS）算法［7］就属于这类变步长算法，其步长因子表达式为：

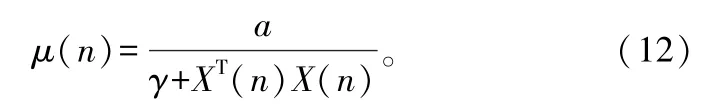
本文采用的变步长LMS算法为：

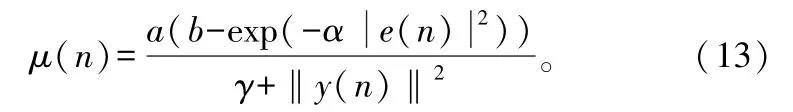
综合考虑上述自适应算法的特点以及本文所选择的功放模型和预失真器模型，提出一种新的自适应算法，即RLS算法和基于Sigmiod函数的NLMS算法的结合应用，初始阶段，选择收敛速度较快的RLS算法，当收敛趋于稳定后，改用NMLS算法，算法原理图如图3所示，当迭代次数n＜N1时，选用RLS算法，当迭代次数n＞＝N1时，选用NMLS算法。

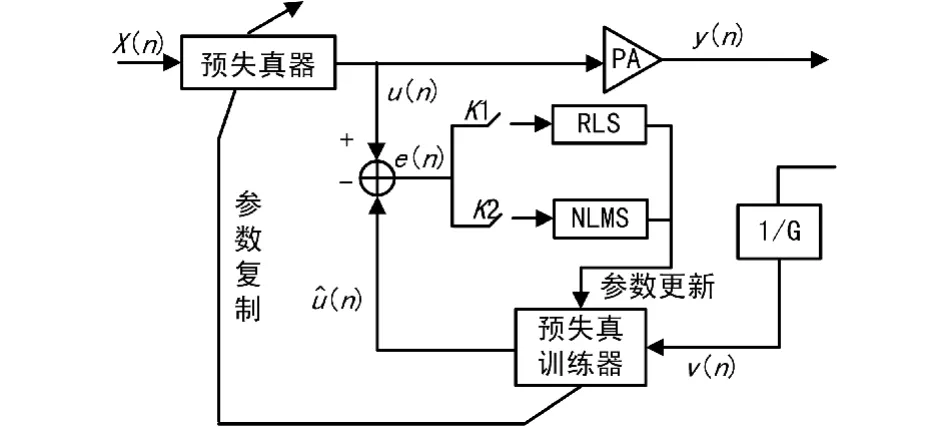
图3 新算法原理图

2 算法仿真及分析

以16QAM信号为实验仿真信号，平方根升余弦脉冲滤波器（主要作用是内插成形）的滚降因子为0.5，上采样为4。功放模型采用Saleh模型，多项式模型（预失真器模型）采用的数学模型如下：

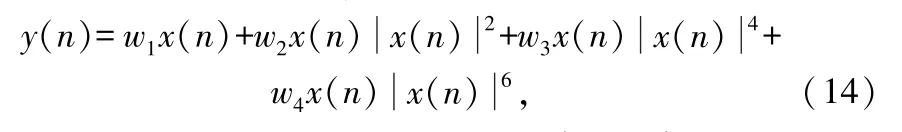
式中，w1、w2、w3和w4为预失真器待更新的权系数。

预失真器的性能由归一化均方误差（NMSE）、输出信号功率谱特征（带内失真和带外抑制2个方面）、误差矢量幅度（EVM）和计算复杂度来衡量。其中EVM是全面衡量通信系统性能的一个重要指标。NMSE的表达式为：

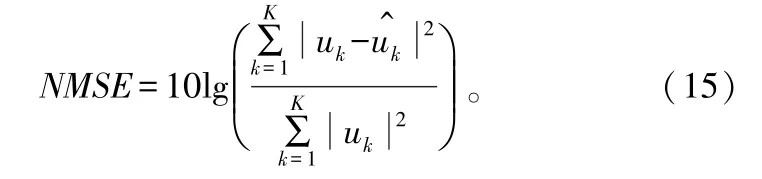
EVM的表达式为：

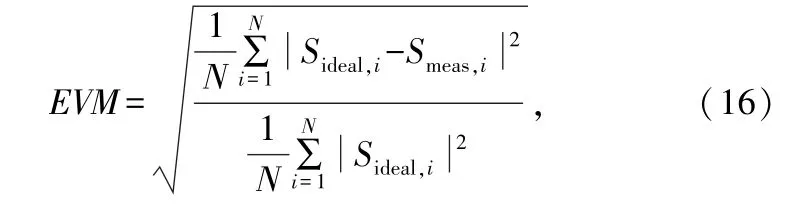
式中，Sideal为参考信号，Smeas为实际测量信号。

当迭代次数小于200时，采用RLS算法，当迭代次数大于200时，采用基于Sigmiod函数的NLMS算法，得到的仿真结果如图4所示，不同信号的EVM值如表1所示。

表1 不同自适应收敛算法所得信号的EVM值

从仿真结果可以看出，NLMS和LMS算法预失真性能较差，RLS和新的组合算法的预失真性能基本一样，但是组合算法的复杂度却大大低于RLS算法。

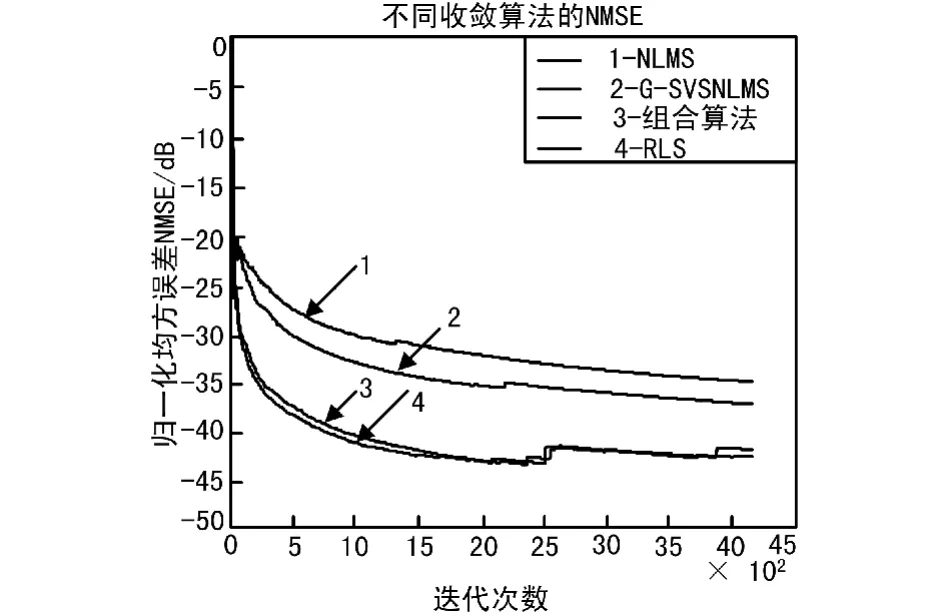
图4 不同自适应算法的预失真性能对比

3 结束语

传统的经典的自适应算法是LMS算法和RLS算法。RLS算法收敛性较好，但复杂度较高；传统的固定步长的LMS算法收敛速度慢，易陷入局部最优且精度不高。本文选择记忆多项式作为预失真器的数学模型，采用RLS和变步长LMS算法相结合的自适应算法的间接学习结构对预失真系统的参数进行辨识，收敛速度得到提升，带内失真得到改善，带外频谱扩展得到了有效抑制。

［1］陈 斌，任国春，龚玉萍.基于多项式与查找表的预失真技术研究［J］.信息安全与通信保密，2011（3）：44－46.

［2］Haykin S.Adaptive Filter Theory［M］.USA：Prentice-Hall，2002.

［3］万 亮，赵庆敏.数字预失真短波功率放大器线性化研究［D］.江西：南昌大学，2010：20－25.

［4］Saleh A.Frequency-independent and Frequency-dependent Nonlinear Models of TWT Amplifiers［J］.IEEE Trans. Commun，1981（29）：1715－1722.

［5］李晓艳，聂明新，余文芳.一种变步长LMS自适应算法噪声抵消算法研究［J］.武汉理工大学学报，20102，3（4）：547－549.

［6］沈大伟，贺 思.一种改进的变步长变更速率LMS自适应滤波算法及仿真［J］.测试测量技术，2010，12：11－15.

［7］张银行，杨辉媛，宋志国.基于归一化LMS算法的自适应滤波器设计［J］.吉首大学学报，2012，33（2）：80－83.

［8］胡春娇，杨 顺.基于箕舌线变步长LMS算法的分析与改进［J］.计算机仿真，2010，27（11）：359－362.

Study of Different Modulation Methods on Digital Pre-distortion in Satellite Communication Systems

HAN Bing，JIN Dong-li
（Beijing Institute of Tracking and Telecommunications Technology，Beijing 100094，China）

Digital pre-distortion is one of the most efficient ways to compensate power amplifier’s nonlinearity.And the choice of adaptive algorithm influences the system pre-distortion performance to some extent.LMS and RLS are frequently-used adaptive conver-gence algorithms.On the base of analyzing the advantage and disadvantage of the two methods，this paper presents a new algorithm，which combines LMS and RLS.Simulation results demonstrate that the new algorithm promotes system pre-distortion performance and lowers the system computational complexity.

Power Amplifier；Digital Pre-distortion；LMS；RLS；Variable Step

TN722

A

1003－3114（2015）06－76－3

10.3969／j.issn.1003－3114.2015.06.20

韩 冰，晋东立.功放预失真中自适应算法研究［J］.无线电通信技术，2015，41（6）：76－78

2015－06－18

韩 冰（1990—），女，硕士研究生，主要研究方向：功放线性化。晋东立（1963—），男，研究员，主要研究方向：航天通信。