噪声环境下Nakagami-m参数估计方法研究

许峻峰，刘志荣

（中国电子进出口总公司，北京 100036）

噪声环境下Nakagami-m参数估计方法研究

许峻峰，刘志荣

（中国电子进出口总公司，北京 100036）

多径衰落信道估计是移动通信系统在实际环境中为了提高接收机性能而迫切需要解决的问题。Nakagami-m参数估计方法主要有盲估计和基于导频信号的信道参数估计方法，重点研究了基于最大似然的Nakagami-m参数盲估计方法，该方法充分利用了最大似然估计是一种最优选择原理，当其概率密度函数取最大值时，可以把m的期望值作为其参数估计值，由此无需导频信号而直接估计出系统的信道系数。理论分析和仿真试验均证明了该方法在噪声环境下的可行性和适用性。

衰落信道；Nakagami-m参数；基于导频信号的信道参数估计；最大似然估计

0 引言

现代无线移动通信系统中为了实现对信号的正确接收，系统往往需要对信道质量进行估计。无线传输系统中的信道估计往往是借助于发送数据中已知的辅助数据来进行的。在接收端，通过将接收到的辅助数据与已知理想数据相比，即可估计相应的信道频响。而在非协作侦察接收系统的设计中由于无法预先知道发送的辅助数据，所以只能采用盲估计算法实现信道参数估计。由此可知，对于Nakagami信道系数分为两大类估计器，即采用导频信号与不采用导频信号的估计方法。显然，盲信道估计算法相比基于导频信号的缺点是算法较复杂，收敛速度比较慢，同时受信道环境、信噪比以及多普勒频率等其他因素的影响较大。

因此，本文首先分析并估计多径衰落信道的基本特征，重点研究噪声环境下Nakagami-m参数的估计方法，研究分析噪声或信道衰落程度对估计方法性能的影响效果，其研究成果将有助于在无线移动通信接收系统中提出克服衰落的有效方法，提高信号正确检测估计和接收的性能。

1 Nakagami衰落信道的数学模型

无线衰落信道的冲激响应可表示为［1］：

式中，L是路径数目，αi是第i条路径上接收信号的复数衰减因子（也称为增益），τi是第i条路径上的传播时延。

设发送信号为：

则接收到的信号为：

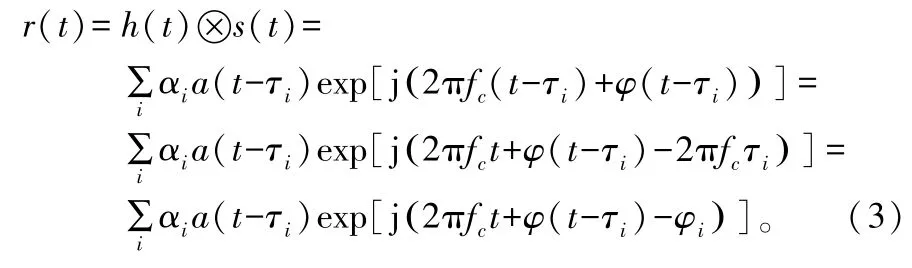
若发射信号为未调制载波传输时，即a（t）＝1，则式（3）中的接收信号为：

其中，

式中，θi（t）为合成信号相位，是均匀分布于［0，2π）的独立同分布随机变量。

当多径传输中有一条起主导作用的较强的传播路径，则路径传输增益是均值为非零常数的高斯随机变量，接收信号的幅度服从莱斯（Rice）分布［2］。

若多径信道中没有起主导作用的路径，此时路径的增益可以近似为零均值高斯随机变量，接收信号的包络服从瑞利（Rayleigh）分布。

大量的分析和实测证明Nakagami分布能够比较接近实际信道的统计特性［3］，更能够比较充分地描述了多径的衰落程度。则第l条路径的传输损耗αl的概率密度函数为：

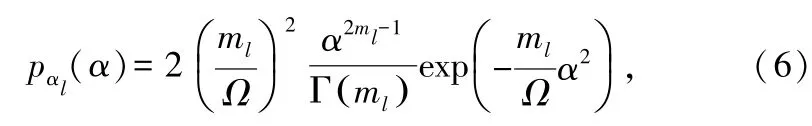
其中，

参数m称为衰落指数，表示为：

在式（6）中，ml参数反映了路径传输衰落的速度和幅度。显然，参数m为1时，为瑞利分布；m＝∞时对应无衰落的情况；当m＝0．5时，为单边高斯分布。莱斯分布和对数正态分布也可以用m＞1的Nakagami分布来近似表示［4］。不同m值时的Nak-agami概率密度函数示例如图1所示［5］。目前，Na-kagami-m参数盲估计方法主要有2类，矩函数估计法［6－8］和极大似然估计法［9］。文献［10］中已经详细论述了基于高阶矩的Nakagami-m参数盲估计方法，所以本文将重点研究基于最大似然估计的Nakagami m参数估计方法。

图1 不同m值时的Nakagami概率密度函数

2 基于最大似然估计的Nakagami m参数估计方法

依照式（6），假设R1，R2，…，RN，为式（6）中的独立同分布随机变量（RV）。所要做的就是根据这些随机变量去评估有效的m参数。基于的R1，R2…RN的独立多元Nakagami分布对数似然方程（LLF）［11］由下式给出：

在这里｛r1，i＝1，…，N｝是｛Ri，i＝1，…，N｝的采样样本。求对数似然方程（LLF）关于m求导，并且设其m＝0。因为是一次求导，这个零值对应于对数似然方程（LLF）的最大值。得到：

式中，ψ（·）是psi函数，也叫digamma函数，定义为ψ（m）＝Γ′／Γ（m）。在式（11）中对m的统计需要求未知的变量Ω。当N趋向于无穷大时，设Ω等于将式（12）代入式（11），产生式（13）。

式（13）左边仅由观测样本决定而且独立于m值［12］。

m参数的最大似然估计需要解非线性方程（13），并不会导出估计表达式的闭和式。ψ（z）的一个渐进展开式如式（12）所给出：

在式（13）中用第1位近似值ψ（z）≈lnz－（1／2z）得到：

用式（13）中第1位近似值ψ（z）＝lnz－（1／2z）－（1／12z2）解m的二次方程12Δm2－6m－1＝0，得到表达式：

去验证Δ＝0的合理性，重写Δ的表达式如下：

当m趋向于无穷大时，Nakagami-m概率密度函数变成落在的冲击函数。相反，当Δ＝0，相反方程（15）和（16）要求m趋向无穷大，这无疑是正确的。

用m的低阶近似值会产生更大的近似值误差。Greenwood和Durand提出他们的按照近似于式（13）的最大似然估计算法式（19）：

不像格林武德的算法适应广泛，在1988年，Bowman［8］提出了一种用式（16）的初始值的备选递归方式如下：

3 性能分析

3.1 试验及数值计算结果

试验一：研究本文的算法与已有的信道盲估计方法的性能比较，即仅仅进行不需要导频信号的盲估计方法性能比较：本文的最大似然算法和基于高阶统计量的谱估计方法。

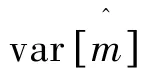
图2为N＝100时的仿真结果。

图2 最大似然估计和矩估计性能比较结果（N＝1 00）

图3为N＝1 000时的仿真结果。由此可见，最大似然法在N＝100时更有效，但是当N增大时会引起更大的偏差，特别是当m值很小时。同时，当N＝1 000时更接近CRLB，而且当N值较小时其性能也不差。图2和图3证明，最大似然法的估计的仿真性能要比基于矩函数的估计方法效果要好。

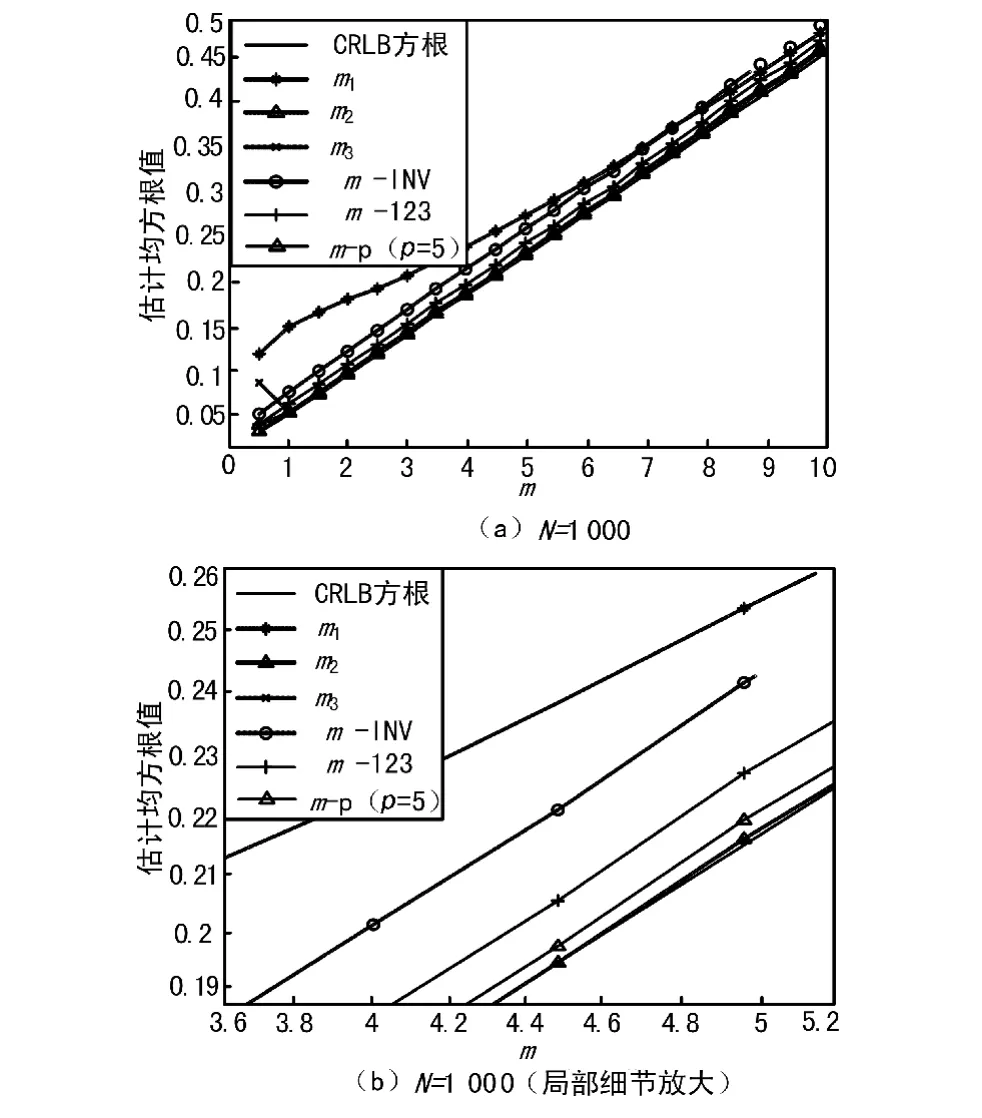
图3 最大似然估计和矩估计性能比较结果

3.2 算法复杂度评估分析

试验二：由于本文重点研究的是无线衰落信道参数的盲估计方法，这类盲估计方法普遍存在运算复杂的问题。文献［10］是基于高阶矩的Nakagami-m参数估计方法，所以为了更客观地评估本文算法的性能，本文依照文献［10］的计算过程操作步骤分解的方法，评估了基于最大似然估计方法的计算复杂度，其结果如表1所示。

表1 噪声环境下的计算量表

乘除法的复杂度显然是高于加减法，所以基于最大似然估计法相比于矩函数方法，复杂度要高一些的。

4 结束语

在非协作通信中，多径衰落信道参数估计方法不仅仅是无导频信号辅助的盲估计，更要普遍适合于噪声环境。盲信道估计算法其共同缺点是算法较复杂，收敛速度比较慢，同时受信道环境、调制方式、信噪比以及多普勒频率的影响较大。在时变信道条件下，即使是慢变信道，这些方法都会出现噪声门限效应。因此，对于非协作通信的侦察接收系统，信道盲估计方法下一步要考虑利用阵列天线和空域滤波处理的方法，利用不同天线阵子接收信号之间的相关性，从时域、频域或空域等不同的角度，进一步提高信道特性的估计准确度。

［1］Proakis J G.Digital Communications［M］.USA：McGraw Hill，2000.

［2］Suzuki H.A Statistical Model for Urban Multi-Path［J］. IEEE Trans Commun，1977，25（7）：673－680.

［3］Ko Y，Alouini M S.Estimation of Nakagami Fading Chan-nel Parameters with Application to Optimized Transmitter Diversity Systems［C］∥Proc.ICC，2001（6）：1690－1695.

［4］Tepedelenlioglu C，Gao P.Estimators of the Nakagami-m Parameter and Performance Analysis［J］.IEEE Trans. Commun.，2005，4（2）：519－527.

［5］Abdi A，Kaveh M.Performance Comparison of Three Dif-ferent Estimators for the Nakagami-M Parameter Using Monte Carlo Simulation［J］.IEEE Commun.Lett，2000，4（4）：119－121.

［6］Cheng J，Beaulieu N.Moment-based Estimation of the Na-kagami-M Fading Parameter［C］∥IEEE PACRIM Conf. Commun Comput.Signal Process，2001，8（2）：361－364.

［7］Gaeddert J，Annamalai A.Further results on Nakagami-m parameter estimation［J］.IEEE Commun Lett，2005，1（9）：22－24.

［8］Gaeddert J，Annamalai A.Some Remarks on Nakagami-m Parameter Estimation using Method of Moments［J］.IEEE Commun Lett，2005，4（9）：313－315.

［9］张 程.基于高阶矩的Nakagami-m参数估计方法［J］.无线电通信技术，2012（2）：13－16.

［10］ChengJ，BeaulieuN.Maximum-likelihoodBased Estimation of The Nakagami-M Parameter［J］.IEEE Com-mun.Lett，2001，5（3）：101－103.

［11］Zhang Q T.A Note on The Estimation of Nakagami-M Fa-ding Parameter［J］.IEEE Commun Lett，2002：6（6）：237－238.

［12］Cheng J，Beaulieu N，Generalized Moment Estimators for the Nakagami Fading Parameters［J］.IEEE Comm Lett，2002，4（6）：144－146.

Nakagami-m Parameter Estimation in Noisy Environment

XU Jun-feng，LIU Zhi-rong
（China National Electronics Import＆Export Corporation，Beijing 050081，China）

Multipath fading channel estimate is a problem，which needs to be solved as soon as possible，for the mobile communica-tion system for the sake of enhancing receiver performance in practical environment.Nakagami-m parameter estimate methods mainly comprise blind estimate and channel parameter estimate based on pilots.This thesis focuses on the research of Nakagami-m parameter blind estimate method on the basis of maximum likelihood.This method takes full advantage of the maximum likelihood estimation as an optimal choice principle.When probability density function takes the maximum value，the expected value of m can be used as its param-eter estimated value.Therefore the channel parameter of the system can be directly estimated without pilot signal.The feasibility and applicability of this method in noise circumstances have been proved by both theoretical analysis and simulation test.

fading channel，Nakagami-m parameter，maximum likelihood estimate

TN911

A

1003－3114（2015）06－37－4

10.3969／j.issn.1003－3114.2015.06.10

许峻峰，刘志荣.噪声环境下Nakagami-m参数估计方法研究［J］.无线电通信技术，2015，41（6）：37－40

2015－03－11

许峻峰（1975—），工程师，主要研究方向：无线电通信与干扰技术。刘志荣（1981—），工程师，主要研究方向：无线电通信与干扰技术。