OFDM-PNC中继系统的信道估计算法研究

赵东来，王 钢，刘春刚，郑黎明，闫泽涛

（1.哈尔滨工业大学 通信技术研究所，黑龙江 哈尔滨 150001；2.深圳航天科技创新研究院，深圳 518000）

OFDM-PNC中继系统的信道估计算法研究

赵东来1，王 钢1，刘春刚1，郑黎明1，闫泽涛2

（1.哈尔滨工业大学 通信技术研究所，黑龙江 哈尔滨 150001；2.深圳航天科技创新研究院，深圳 518000）

物理层网络编码（PNC）因其在提高网络吞吐量、减少传输时延等方面的优越性，已成为近年的研究热点。为了弥补PNC在频率选择性衰落信道中的性能损失，将OFDM调制技术应用到物理层网络编码中，构成了OFDM-PNC系统。重点研究了OFDM-PNC中继系统的信道估计技术，使用Matlab对最小平方（LS）、最小均方误差（MMSE）及基于奇异值分解（SVD）信道估计算法的性能进行仿真，仿真结果验证了理论分析。

物理层网络编码；OFDM；信道估计；LS算法

0 引言

近年，双向中继技术已经成为无线通信的研究重点，2006年，张胜利教授在文献［1］中首次提出了物理层网络编码（Physical-layer Network Coding，PNC），该编码方式在物理层对信号进行处理，有效解决了电磁波干扰的问题，既减少了传输时隙，又提高了网络吞吐量及信道容量。PNC已成为近年研究的热点。PNC与调制技术相结合，可进一步提高信道容量［2］，PNC与信道编码结合不仅能改进系统的可靠性，并且有效降低了中继节点解调和译码的复杂度［3－5］。

在很多研究工作中都假设传输信道为AWGN信道，这显然不符合实际情况，衰落信道的多径时延与频选特性损害了PNC的性能。正交频分复用（OFDM）是一种多载波调制技术，具有抗多径时延及频率选择性和传输速率高等优点，在通信各领域得到了广泛应用［6－8］，将PNC与OFDM技术相结合，恰好可以弥补PNC的不足［9，10］，但国内外在此方面的研究还很少。文献［11］提出了一种最佳功率分配方案，使OFDM-PNC系统信道容量最大化。文献［12］研究了基于物理层网络编码的OFDM-CPM信号在频选衰落信道中的抗干扰性能。

信道估计作为OFDM-PNC系统中关键技术之一，是进行信号检测、均衡的基础［13］，中继节点为了能够有效解调并进行PNC映射必须能够估计信道的相关参数，其估计的准确性直接影响整个系统的性能。本文将研究OFDM-PNC中继系统的信道估计技术。

1 物理层网络编码原理

在三节点无线网络中，A节点和B节点作为信源节点要完成信息交换，但是在实际的通信中，受到很多条件制约，如传输范围限制等，2个节点之间不能直接建立连接，于是在节点A、B之间接入一个中继节点R，A和B通过中继节点作为信息中转点来完成信息交换。相邻节点以帧的形式来发送信息，规定相邻节点完成一帧传输所需时间为一个时隙，这里一帧大小固定。根据网络节点之间信号传输模式的不同分为3种：传统传输模式、网络编码（NC）模式和物理层网络编码模式，如图1所示。在传统网络中，为了尽可能避免噪声干扰，在任何时间，只有一个节点接收或传输信号。完成帧信号Sa，Sb的信息交换共需4个时隙，这种通过时隙低效率的分配来避免数据干扰的方式无疑浪费系统资源，极大地牺牲了系统的吞吐量，而且在多节点网络中显得更加不适用。

图1 3种传输模式

相较于传统通信，NC模式利用了中继节点的信息处理能力来减少传输所需时隙。在时隙1和时隙2，信源节点A和B分别将数据传送给中继节点R，然后在R处异或编码，得到：

在时隙3，R将信号Sr广播发送给A和B，接收端根据本地信息对Sr进行解码，以A为例得到：

同理，B也可以通过相同解码方式得到Sb，相比传统传输机制，网络编码需要3个时隙，系统吞吐量提高了33%。

在PNC传输方式中，中继节点同时接收相邻两个节点的信号，并将接收的电磁波信号叠加。在下一个时隙将处理后的和信号广播给A和B。这样A和B完成信息交换只需2个时隙，相较于传统传输模式和NC传输模式，系统增益提高了100%和50%。

2 系统模型

三节点网络的双向中继OFDM-PNC系统模型如图2所示，信号的传输过程分为2个阶段：多址接入阶段和广播阶段。在多址接入阶段，中继节点同时接收2个信源节点到达的OFDM信号，中继节点根据接收的和信号中的导频信息进行信道估计，然后对和信号进行均衡、检测，映射及OFDM调制，在广播阶段将处理后的和信号同时发给2个信源节点。由以上传播过程可知，中继节点处对上行链路的信道估计将直接影响整个系统的性能，如果估计存在较大误差不但会影响对和信号的处理过程，还会影响下行链路的信道估计和信号检测，使得误差累积，系统的性能受到很大程度的损失。本文将重点研究上行链路的信道估计，并对估计算法的性能进行仿真分析。

图2 OFDM-PNC中继系统模型

下面将用具体的数学表达式对信号传输过程中各个阶段的变化情况进行推导。

2.1 上行链路信号传输过程

信源节点发送一帧数据中包含若干个OFDM符号，每一个OFDM符号由N位信息码元和循环前缀（Cyclic Prefix，CP）组成，为了减少符号间干扰，CP的长度Lcp应大于最大信道时延。用N维矢量分别表示从信源节点A、B发送的第k个 OFDM符号的频域向量，将进行IFFT运算就得到了OFDM符号的时域形式添加CP后就得到了待发射的时域信号

信道模型为多径衰落信道，设节点A到R的信道冲激响应为h1＝［h1（0），h1（1），…，h1（L1－1）］，节点B到R的信道冲击响应h2＝［h2（0），h2（1），…，h2（L2－1）］。信号由A、B同时发送到R，R处接收的和信号为：

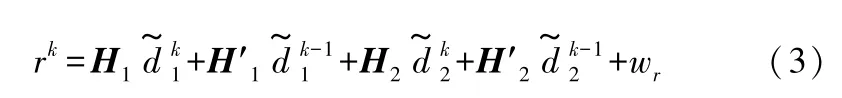
其中，H1、H2、H′1、H′2都是（N＋Lcp）×（N＋Lcp）阶的矩阵，wr为高斯白噪声。

H1、H2表示多径信道对信号的影响，由式（3）可知，时域信号经过信道后相当于信号与信道的冲激响应相卷积。由于各路径的时延不同，各路径信号到达接收端的时间不同，这会使接收的信号产生码间串扰，H′1和H′2即表示上一个OFDM符号对当前符号的影响。

2.2 中继节点对信号的处理

在中继节点进行信道估计之前，要对接收到的和信号去CP及FFT运算。去CP后可得到：

经过推导，得到：

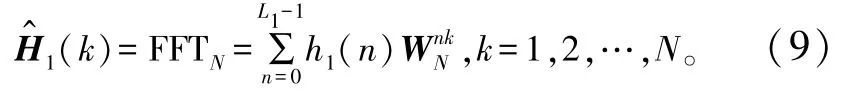
根据发送端的导频信息SP，采用信道估计算法即可估计出信道的频域响应。本文研究了LS算法，MMSE算法在OFDM-PNC系统中的估计性能，下文对两者进行了理论分析和仿真验证。

3 信道估计算法

信道估计算法的2个主要衡量指标是算法的估计性能和复杂度，为了满足实际系统的需求并降低工程上实现的复杂度，选择信道估计准则时通常要在2个指标间折衷，本节将介绍并分析LS、MMSE及SVD算法的性能与复杂度。

可见LS信道估计器结构简单，只需在各载波上做一次除法运算，计算量小。但LS算法没有考虑噪声的影响，所以信道估计的性能会受到噪声和ICI的影响。在信道噪声较大不可忽略时，LS算法的估计性能便大大降低。

基于最小均方误差的信道估计算法充分考虑了信道的统计特性与相关性，采用MSE估计准则，若噪声与信号不相关，则估计值表示为：

式中，Rhh表示导频位置信道冲激响应的自相关矩阵，σn2表示高斯白噪声方差。Rhh＝E（HpHpH）与信道模型有关，在本文所采用的信道模型中，信道各径在CP长度Lcp内均匀分布，功率延时谱按指数衰减。用r（m，n）表示矩阵Rhh第m行第n列的元素。

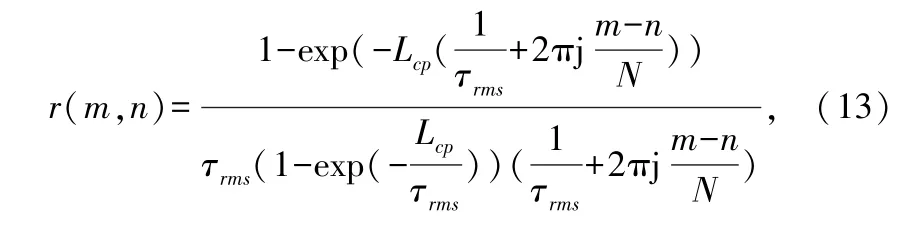
式中，τrms为信道均方时延扩展。

由式（20）可以看出，使用MMSE算法需要进行矩阵的求逆运算，当信道的子载波数增大时，计算量会变得更大，这对硬件的要求很高，从而限制了它的应用。

SVD算法对MMSE算法降阶处理以减少计算量，信道冲激响应的自相关矩阵可进行特征值分解：

式中，U是酉矩阵，Λ＝diag（λ0，λ1，…λN－1），对角线元素是Rhh的N个从大到小排列的特征值。由于信道频率响应的能量主要集中在低频部分，设主要集中在前m阶，在实际系统中Rhh的特征值在m＋1个点后下降得很快，可忽略不计。m的取值要综合考虑估计算法复杂度与估计的准确性，OFDM系统中一般取为CP的长度。将Rhh降秩后代入式（20）可得：

4 仿真分析

用Matlab搭建系统仿真平台，基于三节点PNC传输模型，对中继节点误码率性能进行仿真。系统仿真参数如表1所示。

表1 仿真参数

仿真结果如图3所示。

图3 算法估计性能仿真

由仿真结果可见，LS算法虽然计算比较简单，但是估计的准确性较差，这是因为LS算法没有考虑噪声的影响。MMSE信道估计算法利用信道的统计信息，对信道噪声有很好的抑制作用，与LS算法相比性能提升了5 dB左右，与理想信道估计的性能仅差1 dB，但是算法复杂度较高。在低信噪比环境下，SVD算法不但具有良好的估计性能，而且相对于MMSE算法降低了复杂度。SVD算法是对MMSE算法的降阶简化，只保留了信道能量大的点，滤除了较多的信道信息。因此，随着信噪比的增加，SVD的固有误差将成为制约其性能的主要因素，SVD算法会最先出现平底效应，仿真结果也验证了这一点。

5 结束语

物理层网络编码代表了一种协同通信的理念，其与其他技术相结合还可以从多个方面对网络性能进行优化，PNC与多载波、多信道技术的结合将是下一步的研究重点。将OFDM调制技术应用到物理层网络编码中，OFDM的抗多径时延特性提高了系统的抗干扰的能力，在中继节点处采用经典算法进行信道估计，并结合仿真结果作对比分析。鉴于国内外对OFDM-PNC中继系统的研究还不多，本文为此系统中改进型信道估计算法的提出提供了研究基础。

［1］ZHANG S，LIEW S C，LU L.Physical-Layer Network Cod-ing［C］∥The Annual International Conference on Mobile Computing and Network，2006：358－365.

［2］王静，刘向阳，王新梅.无线网络中基于MPSK的物理层网络编码［J］.高技术通讯，2009，19（2）：147－150.

［3］陈志成，郑宝玉，吉晓东.一种信道编码与物理层网络编码的联合设计［J］.信号处理，2011，27（5）：658－663.

［4］Li J，Chen W，Lin Z，et al.Design ofPhysical Layer NetworkCodedLDPCCodeforAMultiple-Access Relaying System［J］.Communications Letters，IEEE，2013，17（4）：749－752.

［5］Castro M C，Uchôa-Filho B F，Vinhoza T T V，et al.Im-provedJoint Turbo Decoding and Physical-Layer Network Coding［C］∥Information Theory Workshop（ITW），IEEE，2012：532－536.

［6］Zhang Y.Analysis and Simulation of a Low-Voltage Power line Channel Using Orthogonal Frequency Division Multi-plexing［J］.IU-Journal of Electrical＆Electronics Engi-neering，2012，3（1）：89－94.

［7］Danneberg M，Datta R，Festag A，et al.Experimental Tested for 5G Cognitive Radio Access in 4G LTE Cellular Systems［C］∥Sensor Array and Multichannel Signal Pro-cessing Workshop（SAM），2014 IEEE 8th.IEEE，2014：321－324.

［8］Thompson E A，McIntosh C，Isaacs J，et al.RobotCommunica-tion Link using 802.11 n or 900MHz OFDM［J］.Journal of Network and Computer Applications，2015，52：37－51.

［9］Lu L，Wang T，Liew S C，et al.Implementation of Physical Layer Network Coding［J］.Physical Communication，2013（6）：74－87.

［10］Yan H，Nguyen H H.AdaptivePhysical-Layer Network Coding in Two-Way Relaying with OFDM［C］∥Global Communications Conference（GLOBECOM），2013 IEEE. IEEE，2013：4244－4249.

［11］Luo D，Yu Q，Meng W.OptimumPower Allocation for OFDM Iin Physical-Layer Network Coding over a Flat Frequency-Selective Fading Channel［C］∥Information，Communications and Signal Processing（ICICS）2013 9th International Conference on IEEE，2013：1－5.

［12］Sha N，Gao Y，Chen L，et al.OFDM-CPMSignals in Two-Way Relay Channels with Physical-Layer Network Coding［C］∥Information Science and Technology（ICIST），2014 4th IEEE International Conference on.IEEE，2014：747－750.

［13］江淑芬.OFDM系统中基于导频的信道估计的研究［D］.天津：天津大学，2009：22－29.

Research on Channel Estimation Algorithm in OFDM-PNC Relay System

ZHAO Dong-lai1，WANG Gang1，LIU Chun-gang1，ZHENG Li-ming1，YAN Ze-tao2
（1.Harbin Institute of Technology，Communication Research Center，Harbin Heilongjiang 150001，China；2.Shenzhen Institute of Aerospace Science and Technology Innovation，Shenzhen 518000，China）

Physical layer network coding（PNC）has became an important research topic due to its ability to improve the network throughput and reduce transmission delay.In order to make up for the performance loss of PNC in frequency selective fading channel，OFDM modulation technique is applied to the physical layer network coding，constitutes the OFDM-PNC system.This paper mainly studies the channel estimation technology of OFDM-PNC relay system，using Matlab to simulate the estimation performance of least square（LS），minimum mean square error（MMSE）and singular value decomposition（SVD）channel estimation algorithm.The simulation results verify the theoretical analysis.

physical layer network coding；OFDM；channel estimation；LS algorithm

TN919.23

A

1003－3114（2015）06－19－4

10.3969／j.issn.1003－3114.2015.06.05

赵东来，王 钢，刘春刚，等.OFDM-PNC中继系统的信道估计算法研究［J］.无线电通信技术，2015，41（6）：19－22，45.

2015－06－13

国家自然科学基金项目（61401120）

赵东来（1991―），男，硕士研究生，主要研究方向：信道编码、物理层网络编码。王 钢（1962―），男，教授，博士生导师，主要研究方向：信源信道编码、物理层网络编码。