基于有限元理论具有自主清洁功能家用空调的模态分析

2015-06-23高旭峰张启炯吴美霞郑华生

湖北科技学院学报 2015年5期

关键词：家用空调过滤网滤网

高旭峰,张启炯,吴美霞,郑华生,任辉

(武汉科技大学机械自动化学院，湖北武汉 430081)

基于有限元理论具有自主清洁功能家用空调的模态分析

高旭峰,张启炯,吴美霞,郑华生,任辉

(武汉科技大学机械自动化学院，湖北武汉 430081)

根据所设计的具有自清洁功能等的家用空调，分析其模态，确定所设计结构的可靠性，本文以PROE建模，并结合有限元软件对所设计的空调自清洁机构的滤网刷的前5阶模态振型进行分析，分析后结果显示1阶振型为滤网刷在水平面内围绕轴线扭转振动，频率为0.55834Hz；2阶、3阶、4阶、5阶的振型与第1阶类似，且频率分别为1.109 5Hz，1.110 7Hz，2.251 9Hz,2.254 4Hz,滤网刷的旋转频率设定为0.5Hz,其第1阶固有频率为0.558 34Hz，这就加大了滤网刷的振幅，在滤网刷工作时是利用偏心轮对滤网刷的偏心作用清洁空调滤网上的灰尘，当达到共振振幅最大时，清理效果最好。为自清洁空调的设计研发提供理论支持。

有限元；模态分析；可靠性；空调自清洁；振动

家用空调在日常使用过程中无法避免的会在空调内部过滤网积累大量灰尘,当过滤网、蒸发器和送风系统上积聚大量灰尘、污垢时，产生大量的细菌、病毒。这些有害物质随着空气在室内循环，污染空气，传播疾病，严重危害人体健康。本文根据所设计的具有自清洁功能等的家用空调，分析其模态，已确定所设计结构的可靠性，在各种机械结构设计中，由于设计初试的不准确不合适，从而导致机构在运行过程中自身振动过大造成的结构失效已经成为影响产品可靠性的重要原因。因此，在产品设计阶段，依据工程力学理论，借助大型商业化有限元分析软件对产品进行动力学响应分析，可以及时发现结构中存在的问题，在产品试制之前进行有效的整改，可以大大加快新产品研发周期，保证产品的工作可靠性[1]。

一、自清洁空调滤网刷的有限元模型建立

空调自清洁机构的核心部分是内部带有偏心轮的滤网除尘刷，且在该滤网刷内部自带电机，并伴随自身的偏心转动，以达到良好的清除灰尘的目的，在竖直方向上采用丝杆螺母副进行传动，丝杠由另一电机驱动，运行规律是滤网刷自身进行偏心旋转运动，将这一水平位置空调过滤网上的灰尘清理以后停止运行，再由丝杆电机驱动滤网部件在竖直方向移动到另一块空调过滤网的位置，在重复之前的滤网横向运动，如此反复便将空调过滤网上的灰尘清理干净在建立有限元模型时[2]。本文采用PROE先建立空调自清洁机构的三维模型，该机构主要包括丝杆螺母副一对，滤网刷一个，滤网刷驱动电机2个和丝杆螺母驱动电机2个，将整个结构的各部件模型建立好，并将其装配，其机构示意图如图1所示，装配后的三维模型如图2所示[3]。

在进行模态分析时本文主要对滤网刷进行前5阶模态分析，滤网刷的材料为Q235钢，则定义模型的参数为：密度ρ =7.8×103kg/m3，弹性模量E=2.01×1011Pa，泊松比μ= 0.3。所以从Pro/E导入的实体模型类型为体，并在ANSYS中也将单元类型定义为模态分析单元SOLID92 ，设定单元网格尺寸为2，因为滤网刷模型结构简单不复杂，所以划分网格方式为自由划分，最终所得有限元模型单元数为189749，节点数为264560，网格质量较好[4，5]。滤网刷网格模型如图3所示。

图2 空调自清洁机构装配示意图

图3 滤网刷网格模型

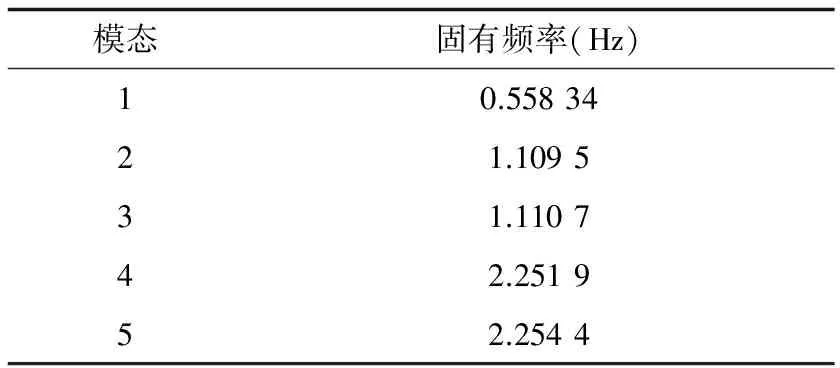
表1 滤网刷模态分析计算结果

图4 滤网刷1阶振型

图5 滤网刷2阶振型

图6 滤网刷3阶振型

图7 滤网刷4阶振型

图8 滤网刷5阶振型

二、模态分析

在进行滤网刷的模态分析时，本文主要采用分块兰索斯(Block Lanczos)法，并设定提取滤网刷有限元模型的前5阶非刚体模态，分析时所定义的边界条件为在11号和20号面添加X,Y,Z方向的位移全约束，并对这两个面加载Y，Z方向的转动全约束，即滤网刷两轴只能在X方向做转动，这样设置满足实际运行条件，其目的在于保证所提取模态信息的准确性[6]。边界条件设定完成，即可进行求解，求解结果如图4-图8，分别为滤网刷1阶振型、2阶振型、3阶振型、4阶振型、5阶振型图。

通过图4-图8可观察到滤网刷的前5阶模态振型特征：1阶振型为滤网刷在水平面内围绕轴线扭转振动，频率为0.558 34Hz；2阶、3阶、4阶、5

阶的振型与第1阶类似，且频率分别为1.109 5Hz，1.110 7Hz，2.251 9Hz,2.254 4Hz,滤网刷的旋转频率设定为0.5Hz,其第1阶固有频率为0.558 34Hz，这就加大了滤网刷的振幅，在滤网刷工作时是利用偏心轮的对滤网刷的偏心作用清洁空调滤网上的灰尘，当达到共振振幅最大时，清理效果最好[7]。