三角形的光栅化与反走样算法

杜慧敏， 郝 哲， 王鹏超， 曹广界， 杜琴琴， 丁家隆

(1.西安邮电大学 电子工程学院， 陕西 西安 710121； 2.西安邮电大学 计算机学院， 陕西 西安 710121)

三角形的光栅化与反走样算法

杜慧敏1， 郝 哲2， 王鹏超1， 曹广界1， 杜琴琴2， 丁家隆1

(1.西安邮电大学 电子工程学院， 陕西 西安 710121； 2.西安邮电大学 计算机学院， 陕西 西安 710121)

针对三角形的光栅化技术，提出一种基于边函数的三角形超采样反走样算法。根据三维平面方程的思想，推导出基于二维平面的属性平面方程的属性插值算法，结合基于Bresenham边步进三角形光栅化算法，对起始基点和反走样点的属性做了修正。实验结果表明，该算法最大工作频率可达到230.631MHz，提高了光栅化的速度。

三角形；光栅化；反走样；属性平面方程

图形处理器[1](Graphics Processing Unit，GPU)的硬件架构经过了五代发展变革，图元光栅化始终是图形处理过程中最重要的处理单元，直接决定着图形的绘制效果和渲染质量。光栅化是由顶点的几何数据和像素数据定义成的基本图元转化成与像素点对应的片元。三角形是图元光栅化中最基本的图元，其光栅化过程包含三角形的参数建立、属性平面方程的建立、边方程的建立和光栅化控制，整个过程包含了大量的算数运算和复杂的状态控制，这已经成为GPU性能的瓶颈。

随着图形渲染模型中每个片元属性值的不断增多，要提高图片显示质量，就需要在光栅化过程中对非毗邻边进行反走样，以此处理更多的运算单元和更大的存储开销。对于采用电池供电的高端移动通讯设备，低功耗、高性能的三角形光栅化反走样算法就需要研究[2-3]。

三角形光栅化现有的方法[4-5],仍然需要处理大量的像素点,同时也需要大量的计算。如果使用软件来处理三角形光栅化,会造成CPU的大量开销和资源利用率的降低。

本文拟在三角形构成的图形中，通过分析基于边函数的三角形光栅化算法，提出一种基于边函数的三角形超采样反走样算法。通过推导基于二维平面的属性平面方程的属性插值算法，结合基于Bresenham边步进三角形光栅化算法[6]，对起始基点和反走样点的属性做了修正。并通过硬件来验证此算法的可行性。

1 三角形光栅化与反走样算法

将三角形的三个顶点按照y坐标值的大小，由小到大分别记作A,B,C，当有一条边水平时(两个点的y坐标相等)，水平边上两个点的顺序任意，如图 1 所示。定义AC边为引导边，AB边为第一跟随边，BC为第二跟随边。 位于引导边与跟随边之间的水平线定义为跨度[7]。

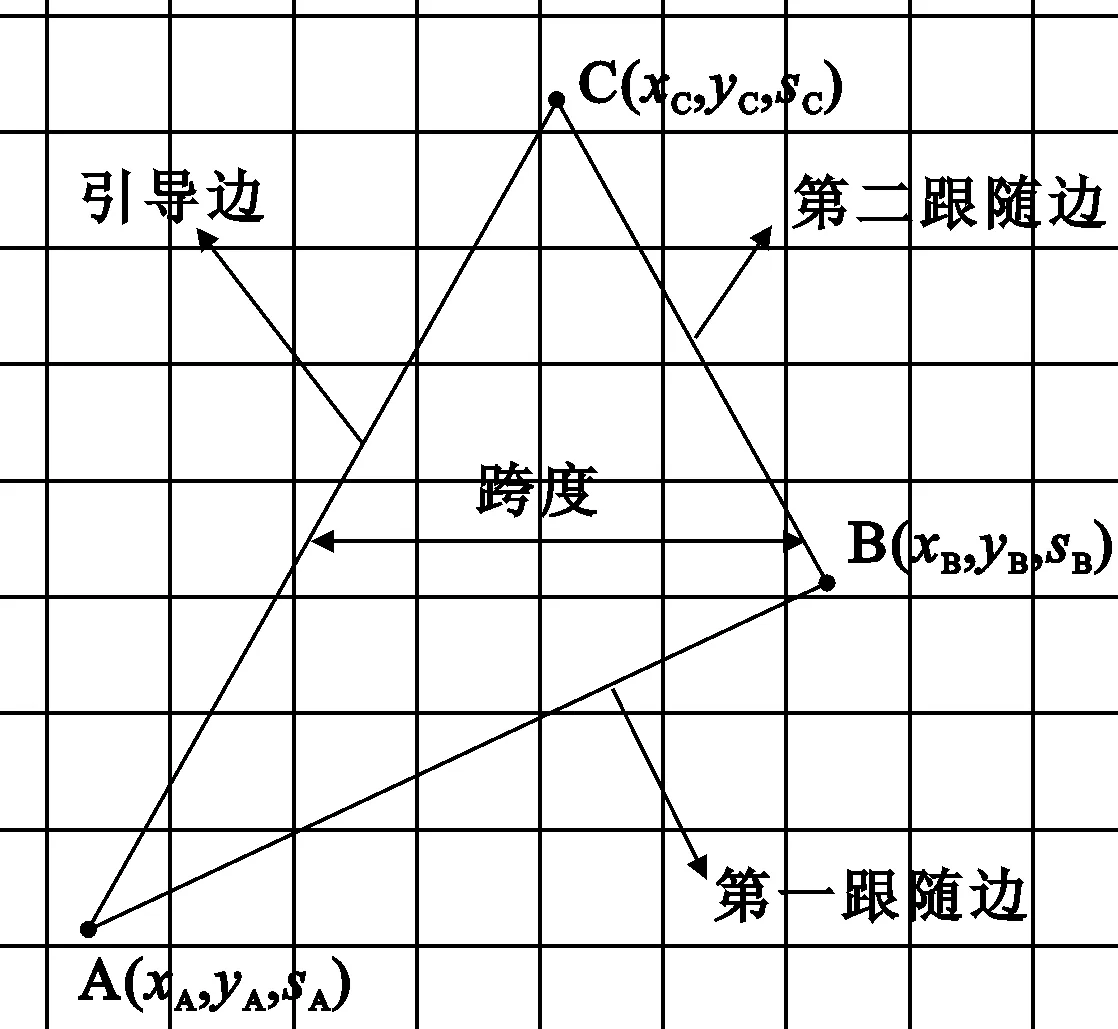
图1 三角形的边的定义说明

1.1 属性平面方程

现代的图形渲染模型中，每个片元附有更多的属性，比如光照的各种颜色、纹理坐标、权重、法向量等。每个片元的各个属性值根据三角形各顶点的属性值进行插值计算。其根据平面方程来推导出属性插值的一般算法。

在三角形的一般方程[8]

ax+by+cz+d=0

(1)

中得知方程系数的值，便可求出这个平面内任一点(x，y)的z值。可以将顶点的各个标量属性参数(包括颜色，纹理坐标，法向量等)统一设为字母s，和式(1)中的z类似，同样可以得到属性平面方程[9]

ax+by+cs+d=0。

(2)

1.1.1 属性平面方程的求解

由式(2)可以推出属性s的函数表达式

s(x,y)=Ax+By+C。

(3)

根据图1中三个点的信息A(xA,yA,sA),B(xB,yB,sB)和C(xC,yC,sC)可以求出系数

a=(yB-yC)(sA-sC)-(yA-yC)(sB-sC),

(4)

b=(xA-xC)(sB-sC)-(xB-xC)(sA-sC),

(5)

-c=area=(yB-yC)(xA-xC)-(xB-xC)(yA-yC),

(6)

其中系数area就是三角形的有向面积[10]，如图2所示。当area>0时，引导边位于左侧，B点位于右侧，三角形ABC是逆时针方向(ccw)；当area<0时，引导边位于左侧，B点位于右侧，三角形ABC是顺时针方向(ckw);当area=0时，三角形ABC的面积为零，三角形退化为一条直线或一个点，此时三角形不需要光栅化。

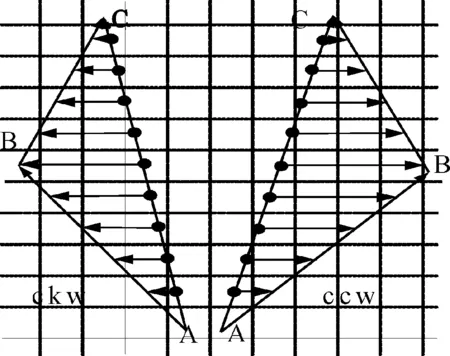
图2 三角形的有向面积

由式(4)(5)(6)可得出A和B的表达式

A=T1(sA-sC)-T2(sB-sC),B=T3(sB-sC)-T4(sA-sC),

其中T1，T2，T3，T4是只与点的坐标有关的参数

对同一三角形的属性s，计算属性平面方程系数时Ti(i=1,2,3,4)值相同，因此只需计算(sB-sC)和(sA-sC)，从而在硬件电路中减小功耗。

1.1.2 属性函数的应用

由式(3)可知，在图3中三角形ABC中，基点O(xO,yO,sO)有

sO=s(xO,yO)=AxO+ByO+C,

(7)

那么对于三角形所在平面内的任意一点P(xP,yP,sP)有

sP=s(xP,yP)=Axp+Byp+C。

(8)

解式(7)和式(8)可得

sP=s(xP,yP)=s(xO,yO)+A(xP-xO)+B(yP-yO)=sO+AΔxOP+BΔyOP,

(9)

即在已知三角形所在平面内的任一基点的属性值和该属性的属性平面方程，就可以求出该平面内所有点的该属性值。

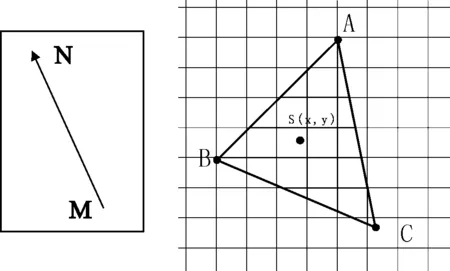
图3 点与三角形矢量边的位置关系

采取自底向顶，子引导边向跟随边的扫描顺序进行扫描，一般选取A为基点。因此其他各点的属性s为

s=sA+AΔx+BΔy。

(10)

1.2 基于边方程的多采样反走样算法

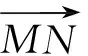
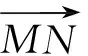
边函数可以计算出像素相对于边的位置，对于一个逆时针排列的三角面来说，判断一个点是否在三角面以内，可以计算出该点对三条边的边界函数

lAB=(x-xA)(yB-yA)-(y-yA)(xB-xA)=a0x+b0y+c0,lBC=(x-xB)(yC-yB)-(y-yB)(xC-xB)=a1x+b1y+c1,lCA=(x-xC)(yA-yC)-(y-yC)(xA-xC)=a2x+b2y+c2。

(11)

若式(11)的计算结果均为正，则点S在三角形内部，否则点S在三角形外部。

一个三角形，若能清楚地判断任意点相对于每一条边的位置，就能够判断出该点的位置。同时使用边函数就意味着从一个像素点被扫描到，到判断出它的位置的时间是固定的。这有利于扫描像素点以流水或并行的方式进行处理。

由上述可知，将一个像素划分成多个亚像素，通过依次判断落在三角形内部的亚像素个数来决定该像素点的覆盖率和渲染强度。如图4所示，将一个像素分为16个亚像素，并根据上述算法描绘出该算法下反走样三角形。

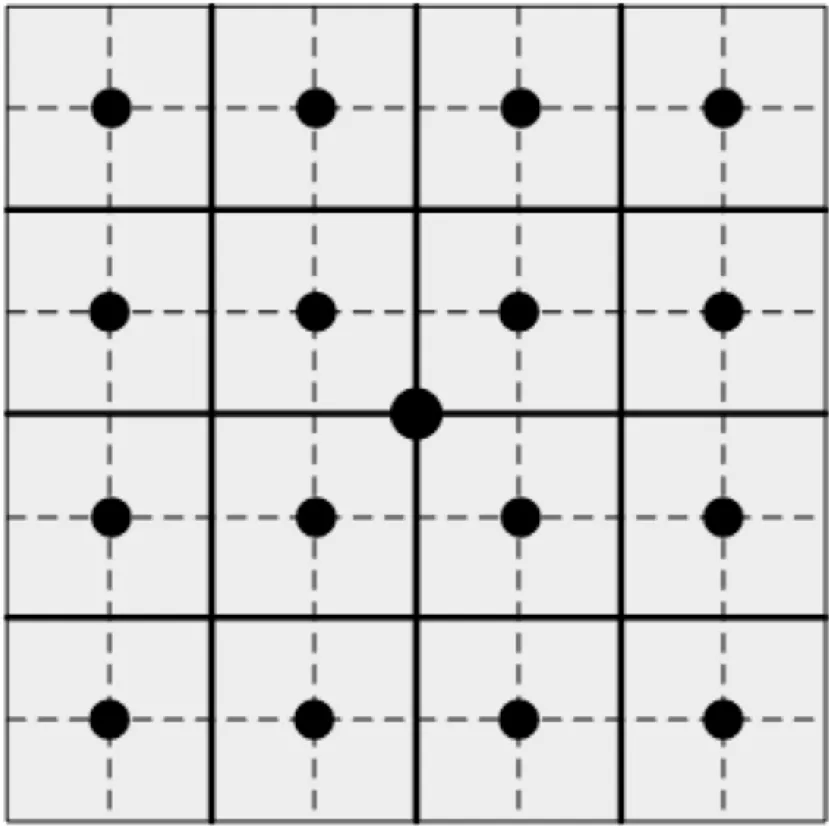
(a) 像素划分

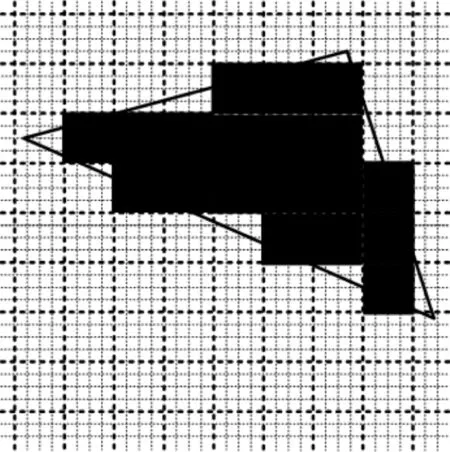
(b) 未启用反走样

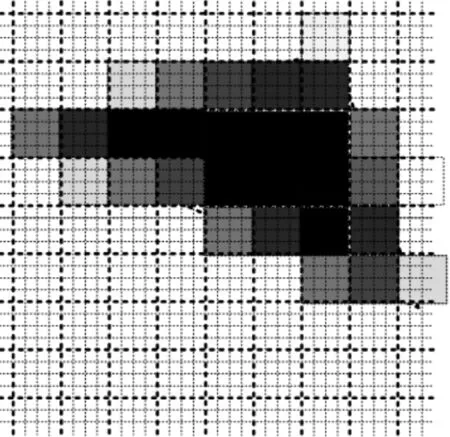
(c) 启用反走样

2 光栅化的参数属性初始化与修正

实际的光栅显示系统中，像素是由具有一定物理大小的方块组成，每个像素对应一个整数坐标。而在光栅化过程中使用的窗口坐标是一个定点小数。因此，应该以像素中心点所对应的属性值作为这个像素点的属性。

2.1 起始迭代参数修正

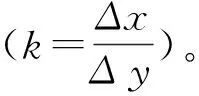
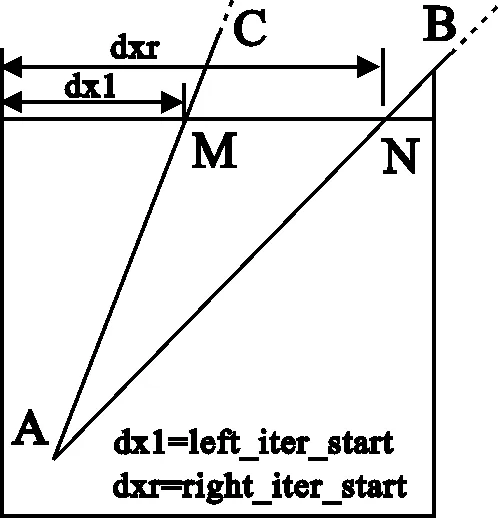
在三角形扫描时，需要引导边和跟随边一起步进，且两条边的决策参数iter_frac的初始值应该修正为图5(a)中的dxr和dxl。

2.2 起始基点的修正

由于整个扫描过程都是整数迭代进行的，式(10)中的Δx和Δy都是整数，因此只需要保证sA是A点所在像素的中心位置的属性值，那么迭代过程中所有像素点的属性值都是该像素中心点的属性值。如图5(a)所示，根据式(10)对A点进行属性修正后得到图5(b)，则

sO=sA+Adx+Bdy。

(a) 扫描的参数属性初始化

(b) 扫描的参数属性修正

图5

2.3 反走样点的属性修正

反走样像素点只有部分位于三角形内部，该像素点属性值不应该再像完整像素那样以像素中心点P的属性值作为该像素点的属性值。根据像素被覆盖的区域，确定出该像素区域被覆盖区的几何中心点的属性值作为该点的属性值。如图6所示，被覆盖区域的几何中心应该为O点，因此通过式(10)对该像素点的属性进行修正，以O点的属性值作为该像素点的属性值。

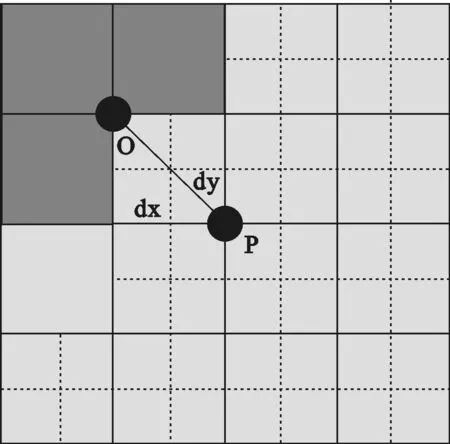
图6 三角形光栅化与反走样整体结构

3 硬件电路设计

三角形图元光栅化与反走样硬件设计结构如图7所示，在三角形扫描转换整体结构中，按照流水线计算顺序可以分为3部分，包括三角形参数建立、属性参数初始化和扫描插值模块。

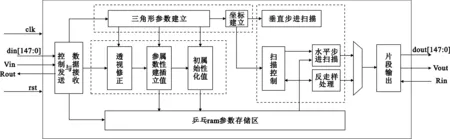
图7 三角形光栅化与反走样总体结构

在图 7 中三角形参数建立单元采用固定功能实现方式。每18个周期可以完成一个三角形光栅化过程所需参数的计算，该模块包含算法中公共部分的计算。属性参数的初始化部分包括透视修正、属性差值参数的建立和属性值初始化3个小单元，此处是一个6级的流水线，负责对所有的片断属性值进行初始化和修正计算。扫描插值模块包括扫描控制、垂直步进扫描、水平步进扫描和反走样处理几个单元。如图8所示，是实现光栅化与反走样过程的控制电路结构。其通过双轨握手协议控制垂直步进模块、反走样模块与水平跨度模块之间的工作。

根据三角形面积的大小扫描时间不定，可以在这些单元的处理过程中都采用流水线的设计方式。扫描峰值时像素生成速率可以达到1个周期出一个像素。

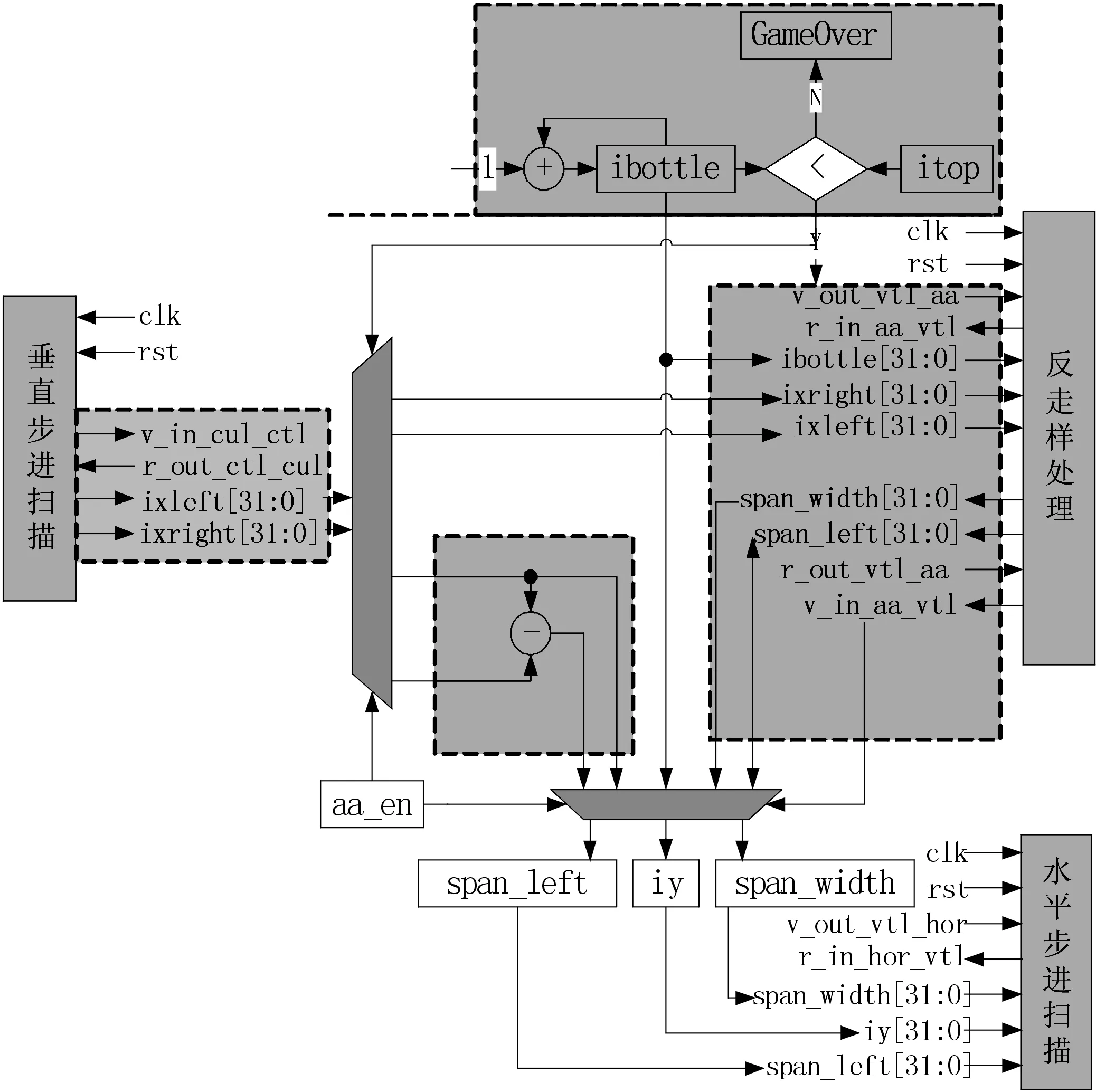
图8 扫描转换的控制电路结构

4 结果验证

为了验证算法的正确性，采用Verilog_HDL完成RTL级的电路设计，使用Xilinx(Virtex6-760)开发系统，对所设计的三角形光栅化硬件电路进行了FPGA验证。结果表明，该算法设计占用了FPGA芯片Virtex6-760：1.79%的资源，最大工作频率为230.631MHz，像素填充速率峰值可达一个像素每时钟周期。

如图9所示是一个兔子，一个没有对基点和反走样点进行属性修正的绘制结果，可以看出在耳朵和曲率比较大的部分有明显的锯齿，并且整个兔子看起来不平滑。

图9 没有经过修正的兔子

图10是经过对基点和反走样点进行属性修正的绘制结果，可以看出这个兔子比没有经过修正的兔子绘制效果更好。对比可见，属性修正是很有必要的，对于提高图形渲染质量也有很大提高。

图10 经过修正的兔子

图11是绘制的不启用反走样和启用反走样情况下星状图。其中左图没有反走样处理，右图经过反走样处理。从图中可以看出，没用反走样处理的测试结果在边界的地方有明显的锯齿走样，而经过反走样处理的测试经过则比较平滑，看起来更加舒服。

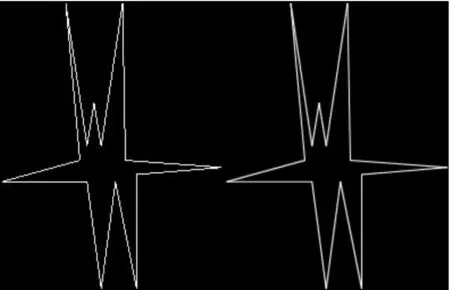
图11 非反走样和反走样的星状

5 结束语

通过分析基于边函数的三角形光栅化算法，提出基于边函数的三角形超采样反走样算法。根据三维平面方程的思想，推导了基于二维平面的属性平面方程的属性插值算法。结合基于Bresenham边步进三角形光栅化算法，对起始基点和反走样点的属性做了修正。总结了整个光栅化过程中公共参数的计算部分，设计出基于硬件资源最大共享化思想和流水线的设计结构。FPGA验证结果表明，该算法能够准确地完成三角形的光栅化。该算法的电路设计很适合集成到移动设备的GPU系统中。

[1] 韩俊刚,刘有耀,张晓.图形处理器的历史现状和发展趋势[J].西安邮电学院学报,2011,16(3):61-64.

[2] 杨国东.嵌入式图像处理器的研究与实现[D].济南：山东大学,2010：8-66.

[3] 田译,张骏,许宏杰,等.图形处理器低功耗设计技术研究[J].计算机科学,2013,40(6A):10-216.

[4] Garachorloo N.Gupta S,Sproull R F,et al.A Characterization of ten Rasterization Techniques[C]//Proc.of the 16th Annual Conference on Computer Graphics and Interactive Techniques .New York ,USA:ACM Press，1989:355-368.

[5] Kaufman A. Rendering, Visualization.Rasterization Hardware[M],NewYork,USA:Springer-Verlag,1993,(6):16-18.

[6] Gaol,Ford.Lumban.Bresenham algorithm implementation and analysis in raster shape[J].IEEE Journal of Computers (Finland) ,2013(1):69-78.

[7] 张鹏,王良.嵌入式图像系统的改进Bresenham反走样算法的应用[J]. 电子设计工程, 2011(4):117-119.

[8] 黄瑞.实时嵌入式图形系统中的三角形光栅化研究与设计[D].上海：上海交通大学,2008：7-12.

[9] 李玉云.面向移动设备的光栅化处理器的研究与设计[D].合肥：中国科学技术大学,2010：8-10.

[10] 吴跃生,李咏秋.关于逆顺三角形有向面积的一个定理及其推论[J].赣南师范学院学报,2010,6(3):31-34.

[11] Chih-Hao Sun,You-Ming Tsao,Ka-Hang Lok et..al.Universal rasterizer with edge equation and tile-scal triangletraversal algorithm for graphics processing unis[J].ICME,2009(6):1358-1361.

[责任编辑:祝剑]

Triangle rasterization and anti-aliasing algorithms

DU Huimin1, HAO Zhe2, WANG Pengchao1,CAO Guangjie1, DU Qinqin2, DING Jialong1

(1. School of Electronic Engineering ,Xi’an University of Posts and Telecommunications,Xi’an 710121,China；2. School of Computer Science, Xi’an University of Posts and Telecommunications,Xi’an 710121,China)

In order to solve the existing problems of the traditional triangular rasterizer technology in a graphics processing unit (GPU), a triangle super sampling aliasing algorithm based on boundary function is proposed. Based on the three-dimensional plane equation, the attribute interpolation algorithm based on the two-dimensional planar plane equation is deduced. By combining stepping triangle rasterization algorithms based on Bresenham edge, some corrections are made in the starting point and anti-aliasing some properties. Experiment results show that the speed of the rasterizer can be improved and the algorithm can achieve maximum working frequency of 230.631 MHz by using the FPGA chip Virtex6-760 authentication.

triangle, rasterization, anti-aliasing, attribute plane equation

2015-01-20

国家自然科学基金资助项目(90607008，60976020)；陕西省政府基金资助项目(2011k06-47)；西安市科技发展计划资助项目(CXY1440(10))

杜慧敏(1966-)，女，博士，教授，从事集成电路设计、计算机体系结构研究。E-mail:228660529@qq.com 郝哲(1987-)，女，硕士，研究方向为计算机体系结构与VLSI。E-mail:648325913@qq.com

10.13682/j.issn.2095-6533.2015.03.005

TP399

A

2095-6533(2015)03-0033-06