基于MATLAB GUI弹簧振子仿真模拟
2015-06-23成海英
成海英, 张 亚
(1.上海电子信息职业技术学院,上海 201411; 2.北京机电研究所,北京 100086)
基于MATLAB GUI弹簧振子仿真模拟
成海英1, 张 亚2
(1.上海电子信息职业技术学院,上海 201411; 2.北京机电研究所,北京 100086)
典型理论模型虚拟实验制作以及虚拟实验室构建已经成为多媒体教学的重要发展趋势之一。利用MATLAB软件GUI功能,对弹簧振子基本模型在模型展示、概念说明、仿真动画、模型规律绘制等进行虚拟实验制作。结果表明:仿真结果规律正确,仿真生动形象。虚拟实验的制作过程对物理学、力学等其它理论模型的仿真具有重要的参考意义。
三维弹簧振子;仿真实验;MATLAB GUI
基本理论问题的仿真作为多媒体教学的重要支撑,具有生动形象、方便快捷、易于操作,不受场地限制等优势,广泛地应用于物理、数学、力学等教学实践中[1-4]。在多媒体仿真动画制作中常用网页设计软件制作动画(如Flash)和计算机语言编程软件(如MATLAB语言、Fortran、VB、C语言等)制作仿真动画两种方式,后者不仅可以真实地仿真物理过程还可以构建虚拟实验,对物理规律揭示更加透彻,已经逐渐成为教学和科学研究的重要工具。此外,计算机语言仿真已成为科学问题研究中除实验研究理论分析外的有力手段[5,6]。MATLAB将矩阵运算、数值分析、图形处理和编程技术结合,其指令代码与数学、工程中常用的形式十分相似,函数库以及工具箱极为丰富,进行仿真实验制作较C、FORTRAN等语言更加简洁方便。MATLAB软件中图形用户界面(GUI模块)不仅形象生动、互动友善、操控灵活,而且为人们提供了定性和定量的结合、局域和全域的结合、时域和频域的结合、模拟和数字结合的数据探索和科学分析的仿真平台。该功能和科学研究、多媒体教学、虚拟实验室构建等方向高度一致,已在科学研究领域影响着研究方式的深刻变化[7]。
现有对弹簧振子模型的研究主要集中在以数值研究的角度对多弹簧振子耦合、非线性弹簧振子、弹簧振子-单摆等耦合系统的研究[8-13],而对于物理实验角度研究鲜为报道。本文以弹簧振子为基本模型,从数值仿真与多媒体教学的角度,利用MATLAB中GUI模块,深入阐述GUI制作中界面设计、动画编程控件编辑等基本问题。
1 弹簧振子理论模型与基本仿真问题实现
1.1 理论模型
如图1所示为弹簧振子基本模型,质量为m的小球在x方向做简谐振动。其中O点位置为平衡位置,A、B两点分别为弹簧振子两个极限位置,初始状态为小球在右极限位置。整个系统的拉格朗日方程为:
(1)
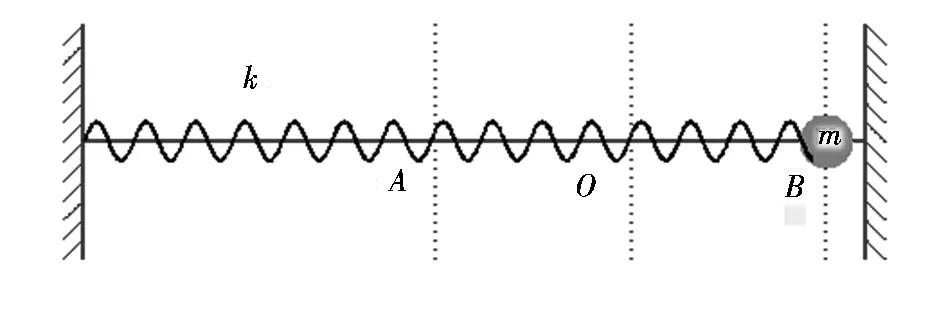
图1 弹簧振子基本模型Fig.1 Basic model of spring oscillator
由拉格朗日方程求出系统的运动微分方程为:
(2)

(3)
(4)
1.2 微分方程求解实现
MATLAB中ode45为解非刚性微分方程命令,中等精度,使用Runge-Kutta的四、五阶算法。其格式如下:
[T,Y]=solver(odefun,tspan,y0,options,p1,p2…)
其中,odefun为求解的常微分方程文件名,方程形式为y′=odefun(t,y);tspan为单调递增(递减)区间[t0tfinal]或[t0,t1…tfinal]; y0为初始条件矢量;options为用ode命令建立的优化选项; p1,p2…为主程序传递给oedfun函数的参数。
本文采用ode45命令求解上述微分方程,根据式(3)、式(4)以及odefun函数编写形式,odefun函数程序如下,并保存为fangz1.m函数文件。
functionydot=fangz1(t,y,flag,k,m)
ydot=[y(2);
-k/m*y(1)];
主程序中设定初始条件为t=0时,y1=0.4,y2=0,即小球在右极限位置,求解语句为:
[t,y]=ode45(′fangz1′,0:0.05:100*pi*sqrt(m/k),[0.4,0],[],k,m);
1.3 动画程序编写与实现
MATLAB主要有彗星轨迹图动画、影片动画和实时动画3种形式[4],其中实时动画对没有改变的背景图案不作更新,只更新运动部分的图案,因此加快了每幅画面的生成速度。MATLAB利用图形对象的 “Erasemode”属性实现在保持背景不变的条件下擦除旧对象,显示新对象,“Erasemode”属性有如下4种,其默认方式为“normal”,本文采用默认方式。
normal 重绘整个显示区,该方式显示图形准确、速度慢。
none 不做任何擦除,在原图像上直接绘图。
xor 擦除旧对象的点,显示新对象的点。
background 把旧对象的颜色变为背景色。
当新对象的属性修改后,应用命令drawnow刷新屏幕,使新对象显示出来。命令drawnow使Matlab暂停当前任务去刷新屏幕,这样在循环下即可实现动画效果。
对于本文研究模型,动画部分对象为弹簧振子小球和弹簧,参考程序如下。其中,对弹簧的处理采用螺旋线形式,采用参数方程画20个导程下的螺旋线,采用plot3命令绘制;小球采用sphere命令绘制。另外,需要注意的是,小球的位置以及弹簧端点位置随着索引变量i值的改变而改变,以此实现多个周期的仿真。
qiu=mesh(0.08*XX+x(1),0.08*YY,0.08*ZZ);
spring=plot3(xx,yy,zz,′color′,[28/255 150/255 48/255],′linewidth′,1.5);…
for i=1:length(x)
tt=0:0.01:40*pi;
yy=r.*cos(tt);
zz=r.*sin(tt);
xx=x(i)./20./2./pi*t;
[XX,YY,ZZ]=sphere(50);
set(qiu,′XData′,0.08*XX+x(i),′YData′,0.08*YY,′ZData′,0.08*ZZ);
set(spring,′XData′,xx,′YData′,yy,′ZData′,zz);
drawnow
2 MATLAB GUI设计
2.1 界面设计与控件属性设置
GUI设计主要分为4个板块,① 弹簧振子模型图展示与受力分析;② 基本概念展示;③ 仿真动画;④弹簧振子能量图绘制。其中小球质量和弹簧劲度系数作为模型初值可调,并设定所需的控制按钮:暂停、继续、退出等。主要控件属性以及各控件主要功能如表1所示。
2.2 各控件回调函数程序与说明
(1)初值界面绘制
在function JIANXIEZD_GN_OpeningFcn(hObject, eventdata, handles, varargin)函数程序中绘制程序的初始界面,其语句同“开始”按钮回调函数按钮相似。

表1 主要控件属性
(2)“受力分析”按钮回调函数
function pushbutton1_Callback(hObject, eventdata, handles) global x %定义全局变量x
axes(handles.axes1) %将axes1设置为当前
plot([x(1)+0.5 x(1)+0.1],[0 0],′r′,′linewidth′,3); %绘制受力示意图直线
fill([x(1)+0.1 x(1)+0.1 x(1)-0.1 x(1)+0.1],[0.025 -0.03 0 0.025],′r′); %填充受力示意图箭头
(3)“能量画图”按钮回调函数
function pushbutton2_Callback(hObject, eventdata, handles)
axes(handles.axes3); %将坐标轴3设为当前
k=str2double(get(handles.edit1,′string′)); %从文本框中获得k值
m=str2double(get(handles.edit2,′string′)); %从文本框中获得m值
[t,y]=ode45(′fangz1′,0:0.05:100*pi*sqrt(m/k),[0.4,0],[],k,m); %求解微分方程
EK=1/2*m*(y(:,2)).^2; EP=1/2*k*(y(:,1)).^2; %计算动能、势能
E=EP+EK; %计算机械能
plot(t,EK,t,EP,t,E,′linewidth′,2); %绘制能量曲线
legend(′动能-时间′,′势能-时间′,′机械能-时间′) %设置图例
xlabel(′时间t/(s)′) ylabel(′E(J)′) %设置x,y标签
axis([0 6 0 1]) %设置坐标轴显示范围
(4)“开始”按钮回调函数
function pushbutton3_Callback(hObject, eventdata, handles)
delete(allchild(handles.axes2));%删除axes2中由JIANXIEZD_GN_OpeningFcn下绘制所有对象。
axes(handles.axes2) %选定axes2为当前坐标轴
L0=1;g=9.8;r=0.07 %设定初值
k=str2double(get(handles.edit3,′string′)); %从文本框中获得k值
m=str2double(get(handles.edit4,′string′)); %从文本框中获得m值
[t,y]=ode45(′fangz1′,0:0.05:100*pi*sqrt(m/k),[0.4,0],[],k,m,g); %求解微分方程xmax=max(abs(y(:,1)+L0)); % 计算坐标系范围x轴最大值
axis([0 1.2*(xmax) -1 1,-1 1]); %设置坐标系显示范围
set(gca,′Xtick′,0:0.1:2,′Xticklabel′,{′-1′,″,″,″,′-0.5′,″,″,″,″,′0′,″,″,″,″,′0.5′,″,″,″,″,′1′}) %自定义x轴坐标刻度
t=0:0.01:40*pi; %选定运行时间为40π s。
view(20,20) %设定视角
line([0 1.8],[0 0],[0 0],′color′,[23/255 58/255 103/255],′linewidth′,2); %画中心线
X=[0 0 0 0 0];Y=[0.5 0.5 -0.5 -0.5 0.5];Z=[0.5 -0.5 -0.5 0.5 0.5]; %设置左侧平面边框坐标
C=[0 0 0 0 0]; %填充颜色向量
fill3(X,Y,Z,C,′EdgeColor′,′blue′); %绘制左侧平面
yy=r.*cos(t);zz=r.*sin(t);x=L0+y(:,1); xx=x(1)./20./2./pi*t;%计算弹簧数据
text(x(1),0,-0.15,′B′,′fontsize′,12) %标记右极限位置
text(L0,0,-0.15,′O′,′fontsize′,12) %标记平衡位置
text(L0-(x(1)-L0),0,-0.15,′A′,′fontsize′,12) %标记左极限位置
spring=plot3(xx,yy,zz,′color′,[28/255 150/255 48/255],′linewidth′,1.5); %绘制弹簧
[XX,YY,ZZ]=sphere(50); hold on %绘制小球数据及打开叠加绘图
lighting phong %设置光照属性
qiu=mesh(0.08*XX+x(1),0.08*YY,0.08*ZZ); %绘制小球
axis equal %设定纵、横坐标轴等长刻度
light(′Position′,[x(1)-0.3 -0.6 1],′Style′,′local′) %设置光源位置
material shiny %设置小球材质属性
colormap (gray) %设置颜色条属性
set(qiu,′FaceLighting′,′phong′,′FaceColor′,′interp′,′AmbientStrength′,0.3);%设置小球自身属性
for i=1:length(x) %仿真循环开始
tt=0:0.01:40*pi; yy=r.*cos(tt);zz=r.*sin(tt);xx=x(i)./20./2./pi*t; %计算弹簧数据
[XX,YY,ZZ]=sphere(50); %计算小球数据
set(qiu,'′XData′,0.08*XX+x(i),′YData′,0.08*YY,′ZData′,0.08*ZZ); %设置小球句柄坐标值
set(spring,′XData′,xx,′YData′,yy,′ZData′,zz);%设置弹簧句柄坐标值
drawnow %刷新屏幕
(5)“暂停”按钮回调函数
function pushbutton4_Callback(hObject, eventdata, handles)
uiwait(gcf) %图形界面暂停
(6)“继续”按钮回调函数
function pushbutton5_Callback(hObject, eventdata, handles)
uiresume(gcf) %图形界面继续
(7)“退出”按钮回调函数
function pushbutton6_Callback(hObject, eventdata, handles)
close %关闭图形界面
3 实验结果与讨论
图2所示为程序运行结果,由运行结果可知,仿真动画连续生动,三维效果逼真,达到了预期效果,通过教学实践,在课堂上取得较好的效果。同时,本文所提出的仿真实验也可作为虚拟实验使用,通过测量不同k和m值可以得到弹簧振子周期与k值成正比与m成反比的结论。另外,该运行程序可以通过mcc命令编译生成可执行文件,方便在常用电脑上运行。

图2 弹簧振子实验仿真界面Fig.2 Simulation interface of spring oscillator test
4 结 论
本文主要以弹簧振子为基本模型,设计了MATLAB GUI仿真实验,该虚拟实验将抽象复杂的概念用生动仿真表现出来,并可作为虚拟实验使用。本文提出基本物理模型的GUI虚拟实验设计方法,可以使通过虚拟实验对物理概念、物理规律以及能量转化理解更深入。虚拟实验制作以及虚拟实验室平台构建将是多媒体教学的一个重要发展方向,具有广阔的应用前景。
[1] 蒙成举,苏安.Matlab辅助磁场描绘实验教学研究[J].河池学院学报,2010(S1):108-111.
[2] 朱卫娟,孔祥鲲.磁感应强度仿真实验——MATLAB在物理教学中的应用[J].电脑知识与技术(学术交流),2007(16):1 119-1 120.
[3] 陈胤,刘加海.基于Matlab的数值模拟和动画仿真在多媒体教学中的应用[J].计算机时代,2006(8): 60-61.
[4] 彭芳麟.理论力学计算机模拟[M].北京: 清华大学出版社, 2001.
[5] 成海英,陈冬冬,张亚.基于MATLAB的圆孔衍射实验模拟[J].盐城工学院学报:自然科学版,2011(2):11-13.
[6] 成海英,张亚,陈冬冬.基于弹簧耦合的椭圆摆的仿真研究[J].淮海工学院学报:自然科学版,2011(2):23-27.
[7] 张志涌.精通MATLAB R2011a[M].北京:北京航空航天大学出版社,2011.
[8] 何松林,黄焱,戴祖诚.对称双弹簧振子横向振动的复杂性研究[J].昆明学院学报,2010(3):86-88.
[9] 杨正波,夏清华,刘思平.多弹簧振子耦合系统运动研究[J].大学物理,2010(4):29-32.
[10] 杨正波,夏清华.耦合弹簧振子系统的研究[J].高等函授学报:自然科学版,2008(1):15-17.
[11] 钱忠华,周莉英,董慎行.一类非线性弹簧振子的周期性振动[J].物理与工程,2003(4):13-15.
[12] 陈清梅,颜素荣,安红.一种新的“弹簧振子-单摆”耦合摆研究[J].力学与实践,2008(6):93-95.
[13] 谢善娟.用MATLAB分析非线性弹簧振子的振动[J].赤峰学院学报:自然科学版,2009(4): 7-8.
(责任编辑:张英健)
Simulation of Spring Oscillator Based on MATLAB GUI
CHENG Haiying1, ZHANG Ya2
(1.Shanghai Technical Institute of Electronics & Information, Shanghai 201411, China;2.Beijing Rerearch Institute of Mechnical and Electrial Technology, Beijing 100086, China)
The making of virtual test with typical theory model and the establishment of virtual laboratory have become one of the important trends of multimedia teaching. The virtual experiment of spring oscillator, which contains several aspects, such as model display, concept explanation, simulation animation and model’s rule drawing, was made by using the GUI function of MATLAB software in this paper. The results show that the simulation results law are correct and vivid, The production process of virtual experiment in this paper, has the important reference significance on other theory model test simulation in physics and mechanics.
3D spring oscillator; simulation experiment; MATLAB GUI
10.16018/j.cnki.cn32-1650/n.201504005
2015-07-12
上海市教育委员会2013年度教育信息技术应用研究项目
成海英(1977-),女,江苏盐城人,高级讲师,硕士生,主要研究方向为物理问题数值模拟。
O32
A
1671-5322(2015)04-0017-05
