一种变步长自适应算法在GPS空时抗干扰中的应用*
2015-06-23董李梅
董李梅
(成都天奥信息科技有限公司,四川 成都 610041)
一种变步长自适应算法在GPS空时抗干扰中的应用*
董李梅
(成都天奥信息科技有限公司,四川 成都 610041)
GPS空时二维联合抗干扰处理算法能将强干扰以及多径干扰的强度抑制到接近噪底,并且不会对原信号产生严重的损失或者扭曲。研究发现它的干扰抑制性能优于纯空域滤波。但是此算法比纯空域算法的复杂度高,因为需要处理的采样数据协方差矩阵的维数很大,很难做到实时处理。为了解决这一问题,目前工程中普遍采用的是最小均方误差算法(LMS)。通过分析功率倒置(PI)算法,给出了一种变步长的最小均方误差算法(NLMS)。此算法的干扰抑制性能优于最小均方误差算法,能达到多级维纳滤波算法(MSWF)的抑制效果,满足工程需要,并且运算量低,运算时间短,具有更好的可行性和实用性。并将此算法与LMS和MSWF算法进行了仿真对比,验证了其有效性。
空域滤波 抗干扰 最小均方误差算法 多级降秩维纳滤波
0 引 言
全球定位系统(GPS)为人们提供一个精确的3_D位置,并且通过追踪连续谱信号的到达时间还能提供一个精确的速度。人们希望当出现强干扰和多径干扰时,GPS接收机都还能正常工作。对于窄带干扰,有空域滤波,频域滤波,变换域抑制[1]等算法,这些算法都能有效地抑制干扰,但是当出现宽带干扰,尤其时多径干扰时,以上算法就不能适应。为了解决这个问题,自适应阵列天线就应运而生。自适应阵列技术是利用空间自由度在干扰方向形成零陷。
空时联合干扰抑制技术[2],提高了在频域上对干扰的分辨能力,随着时间延迟线长度的增加,时域滤波的描述更准确,频域分辨更精细,在抑制干扰的同时使有用信号损失减小。该技术克服了空域滤波的不足,在不增加阵元的前提下,大大增加了阵的自由度,从而增加了可以处理的干扰数目。该技术的应用使信号处理从联合空时二维域整体考虑,自适应算法设计更加灵活、有效,较一般抗干扰处理抗干扰能力明显加强,适合应用在GPS接收机上。对于空时处理算法最大的问题就是采样数据协方差矩阵维数大,直接进行矩阵求逆的话在现有硬件条件下很难实现。后来提出了多级维纳滤波和LMS等算法来逼近矩阵求逆的解,但是多级维纳滤波算法的运算量大,很难做到实时处理,虽然LMS算法计算量小,权值更新快,但是它的干扰抑制性能差。本文在分析了GPS空时自适应抗干扰基本原理[3]和功率倒置算法[4]的基础上,提出了一种变步长的自适应LMS算法,此方法具有收敛性能好、收敛速度快、自适应权矢量的更新速度快、计算量低,易于工程实现等优点并且干扰抑制性能能达到实际使用的要求。
1 空时联合抗干扰(STAP)基本原理
空时阵列处理器结构见图1。图1中的每个抽头的时间延迟为T,并且要求T<1/B,B是信号带宽。自适应FIR滤波器能对宽带干扰形成干扰零陷。每个自适应FIR滤波器的长度(P-1)T要足够长才能均衡不同的多径延迟。空时阵列处理算法就是选择自适应权值wmp保留GPS有用信号的同时抑制干扰。
当选择的权值wmp如图1所示接收每颗GPS卫星信号和干扰信号。信号和干扰信号产生的向量vm(t)入射到阵元m上时,这个信号被接收并下变频产生向量xm(t)输入到FIR滤波器。假设第m个阵元的第p个抽头接收到的信号为
xm(n-(p-1)T)(m=1,2,…,M;p=1,2,…,P)
(1)
式中,M阵元数,P为每个天线的抽头数。设第m个阵元的第P个抽头的权值为wmp,则每个FIR滤波器的输出为
(2)
若写成矩阵形式为
y=wHx
(3)
式中
w=[w11,…,w1P,…,wM1,…,wMP]T
(4)
x=[x1(n),…,x1(n-(P-1)T),…,xM(n),…,xM(n-(P-1)T)]T
(5)
图1中,共有M个天线,将每个天线接收到的数据延迟P次,P次延迟形成了一个时域FIR滤波器;并且相同时刻的延迟数据有M个天线接收,因此每次处理不仅有空域数据还有时域数据。对于每个阵元通道,抽头延时构成了FIR滤波,使得它可以在时域上抑制干扰;对于相同时刻的延迟节点,各个阵元构成了空域的自适应滤波,使得它可以在空间上分辨干扰源,形成空域零陷抑制空域干扰。从上可以知道空时阵列处理是空域天线阵列在时域上的扩展,这相当于在不增加天线数的前提下增加了滤波器的自由度,比单纯的空域滤波能滤除更多的干扰,并且能更有效的抑制宽带干扰。
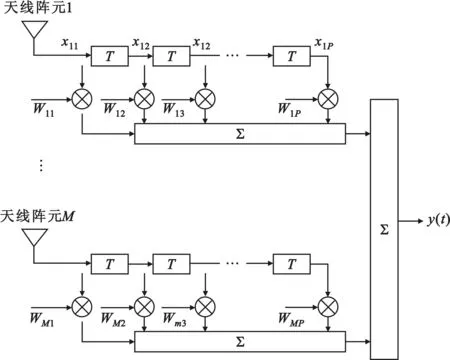
图1 空时联合阵列处理结构
2 自适应滤波的最优化准则
线性约束最小方差(LCMV,Linearly Constrained Millimulil Variance)、最大信干噪比(Maximum Signal to Interference and Noise Ratio)和最小均方误差(MMSE,Minimum Mean-square Error)等准则是GPS接收机抗干扰算法中常用的自适应准则。目前工程上常用的自适应准则是LCMV。
2.1 线性约束最小方差(LCMV)准则
线性约束最小方差准则是满足一定的线性约束条件(通常使用如式(6)所示的约束条件)下使信号功率最小。当式(6)中的常数c=1时此算法也称为功率倒置算法(PI)。
minwHRwsubject towHS(θ,φ)=c
(6)
S为导向矢量,θ为方位角,φ为俯仰角,R=E{x(n)x(n)H})为阵列接收信号(有用信号、干扰信号和噪声的叠加)的采样数据协方差矩阵。LCMV算法最优权值向量为
(7)
为了便于工程实现通常选择功率倒置算法。
2.2 功率倒置算法权向量的求解
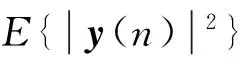
(8)
其中
Rxx=E{x(n)(x(n))H}
(9)
为输入采样数据协方差矩阵。
构建拉格朗日代价函数:
L(w)=wHRxxw+λ(wHS-1)
(10)
其中,λ为拉格朗日乘数。
(11)
2.3 自适应变步长最小均方误差(NLMS)算法
式(11)涉及到矩阵求逆,由于采样数据的协方差矩阵很大,从而使得在硬件上实现大型矩阵的矩阵求逆变得很复杂,且实时性差,很难满足工程需要。通常工程上为了避免矩阵求逆,采用最陡下降法得到最优权向量w的递归表达式,推导如下:
先设置一个w的初始值w(0)=[1,0,0,…,0]H,再让w沿着Pout减小最快的方向即负梯度方向变化。因此得到
w(n+1)=w(n)-μwPout+aS
(12)
式(12)中,μ为可调的步长因子,wPout对w的梯度,a的作用是使wHS=1始终成立。
已知
[w(n+1)]HS=1
(13)
因此
[w(n)-μwPout+aS]HS=1
(14)
从而求得
a=1-[w(n)-μwPout]HS/SHS
(15)
将a的值带入式(12)可以求得权向量的递推公式:
w(n+1)=w(n)-μwPout+μSSH/SHSwPout
(16)
工程上通常采用固定步长的μ来进行权值更新,称为LMS算法。当干扰信号的功率强弱变化时,LMS算法的收敛速度会变慢,干扰抑制性能下降,有时甚至导致算法无法收敛,丧失干扰抑制的功能。因此,步长μ的自适应调节将变得至关重要。故NLMS算法的性能将会优于LMS算法,并且通过仿真发现它能达到多级维纳滤波[3]算法的干扰抑制性能。
2.4 自适应变步长调节算法
自适应步长的调节算法推导:
设置一个功率值P,单位为能量,首先在无干扰信号的情况下将输入信号的进行固定时间的信号功率积分,积分值为power_value,因此得到
gain=P/power_value
(17)
式(17)中的gain称为增益因子。
其次在一个已知干扰功率为p_antj,单位为dbw的情况下,根据式(17)得到
c=(gain^2)*10^(p_antj/10)
(18)
式(18)中的c称为常量因子。
然后由常量因子c得到
step=10*log10(c/gain^2)
(19)
最后根据式(19)得到一个相对应的步长因子μ。
3 算法仿真与分析
3.1 仿真条件
中心频率f0=1 575.42 MHz;带宽B=2 MHz;阵元形式:均匀园阵;阵列形式:4元阵,阵元间距d:中心频率半波长;图2所示,设干扰信号J(t)以(θ,φ)角度入射,θ为方位角,φ为俯仰角;有用信号参数:功率设置为-130 dbmW,信噪比-20 dB,为经C/A码调制后的扩频信号,入射角度为(60°,70°);由于仿真采用的是4元阵,所以最多只有三个宽带干扰。三个宽带干扰信号参数:带宽分别为2 MHz、1.4 MHz和0.8 MHz,干噪比为40 dB,入射角度分别为(20°,30°)、(180°,50°)和( 240°,60°)。
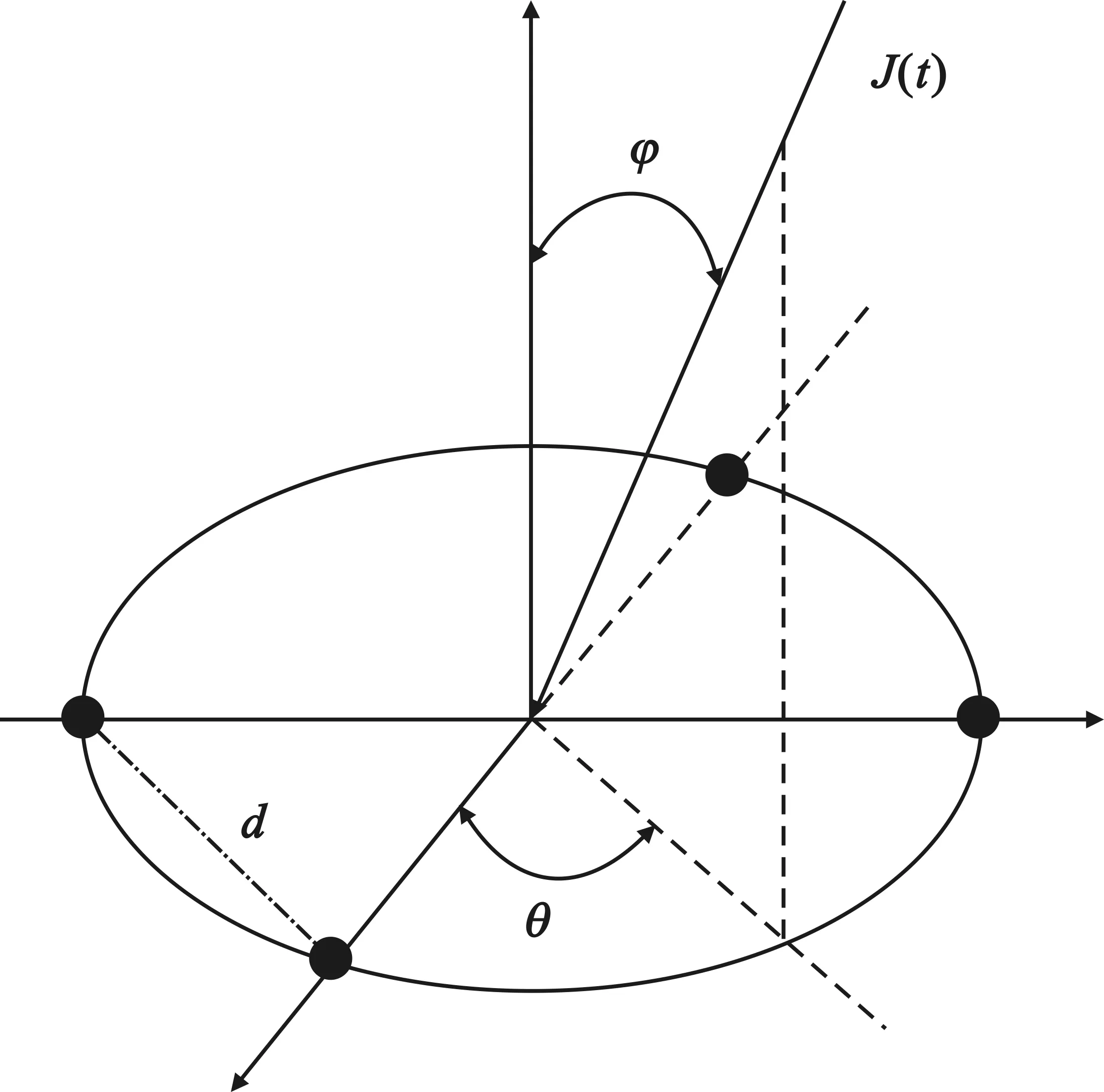
图2 阵列分布
3.2 算法收敛性和干扰抑制性能分析
(1) 假设时延抽头数为3,空时联合处理分别采用LMS,NLMS和多级维纳滤波算法。仿真中只有一个宽带干扰信号,入射角度分别为(20°,30°),带宽为2 MHz,干噪比为30 dB。前两个算法收敛情况见图3和图4,三个算法各自的自适应调零天线的方向如图5,图6和图7所示。
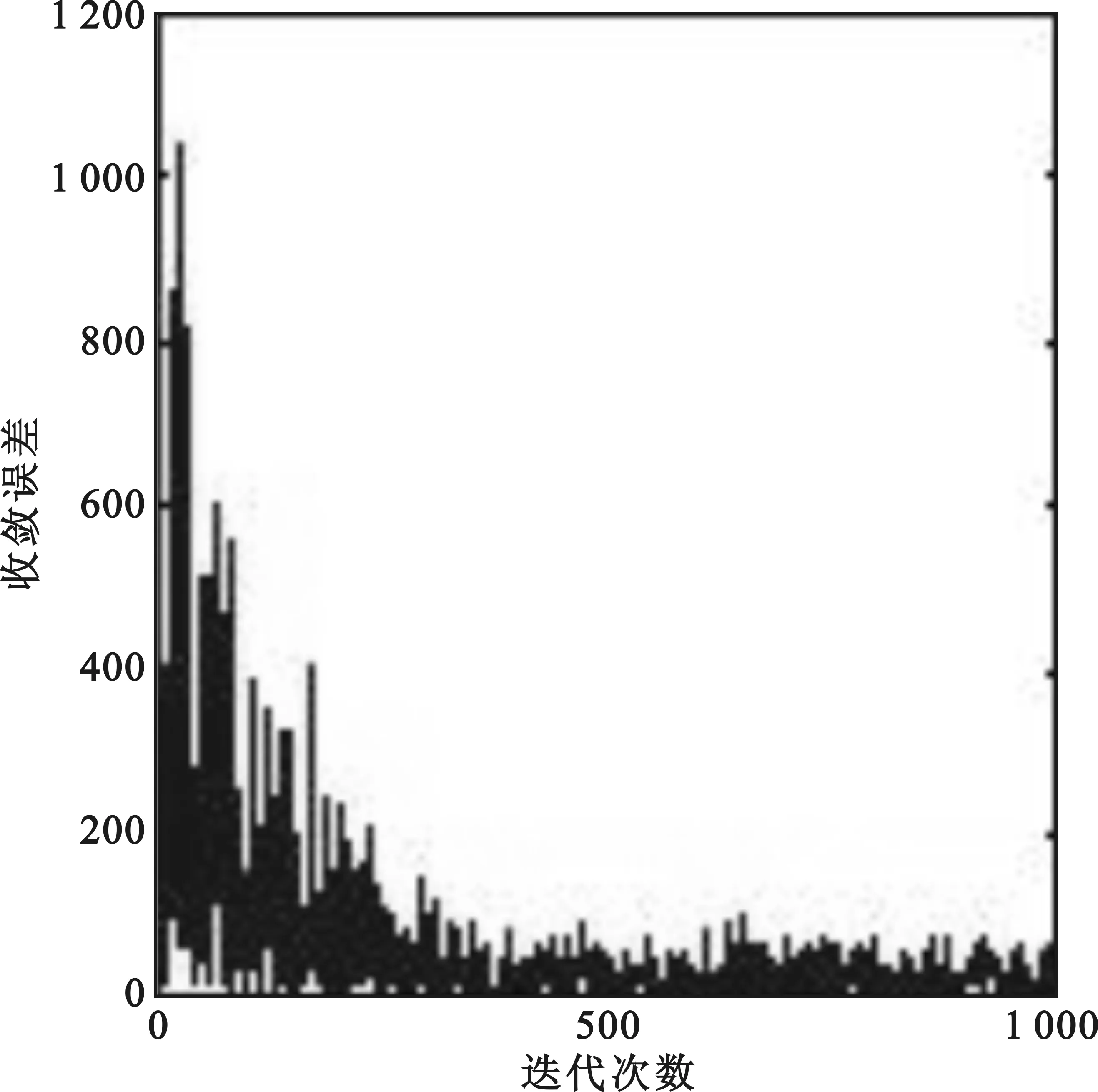
图3 信号输出误差
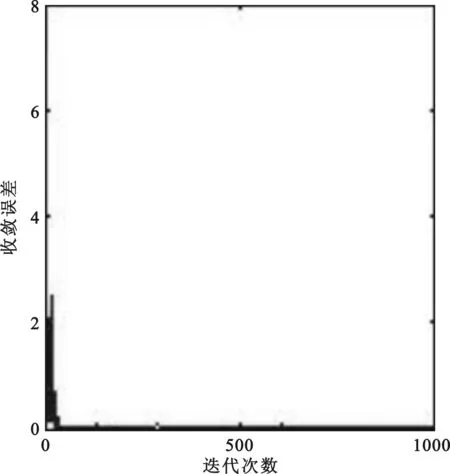
图4 信号输出误差
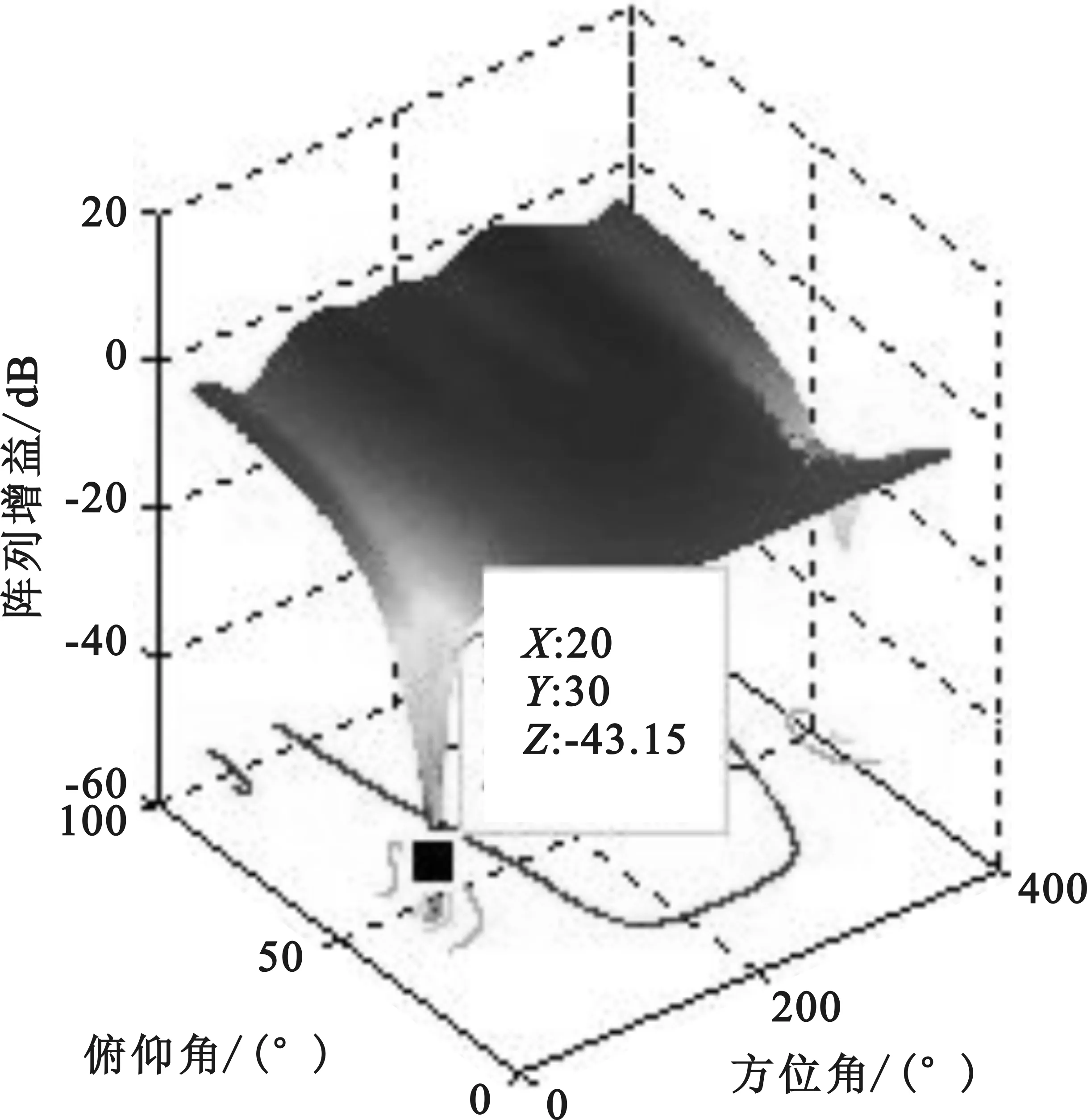
图5 阵列天线方向
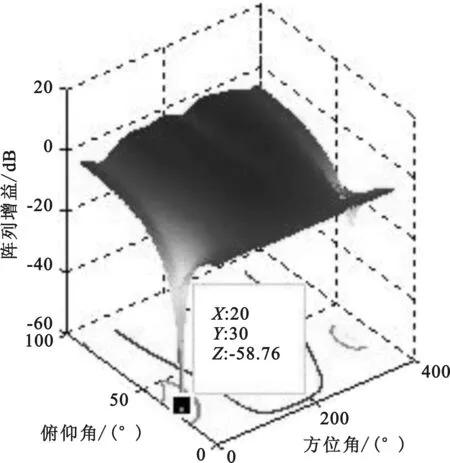
图6 阵列天线方向
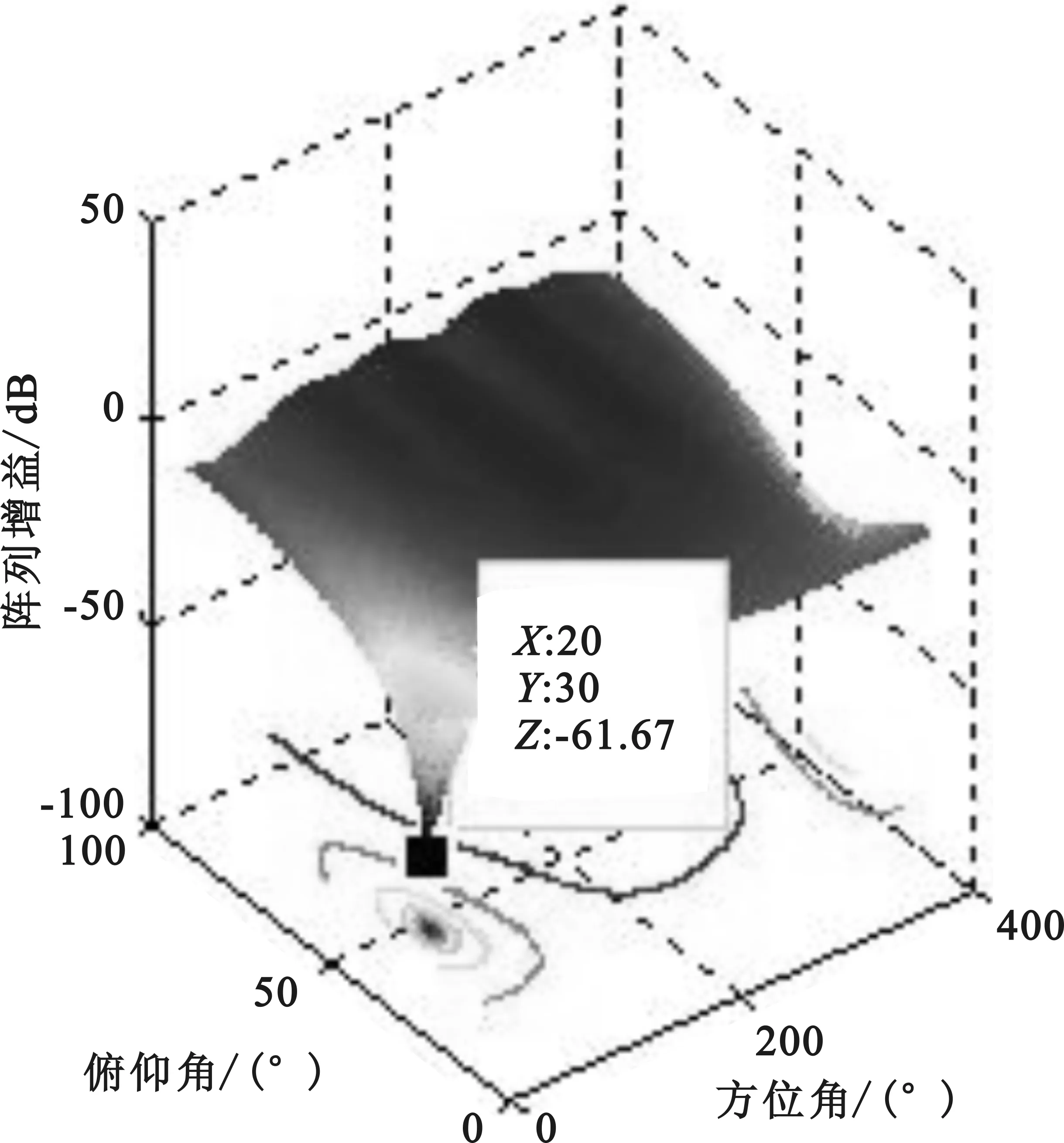
图7 阵列天线方向
从图3和图4可看出NLMS的收敛速度比LMS的快,并且从图5,图6和图7还可看出,NLMS的零深比LMS的零深深,干扰抑制性能好,并且NLMS的零深和多级维纳滤波算法的零深基本一致,因此采用NLMS算法的干扰抑制性能能达到多级维纳滤波算法的性能。
(2)仿真中有两个宽带干扰信号,入射角度分别为(20°,30°),(180°,50°),带宽为2 MHz,1.4 MHz,干噪比为30 dB。前两个算法收敛情况见图8和图9,三个算法的自适应调零天线的方向图如图10,图11和图12所示。

图8 信号输出误差曲线
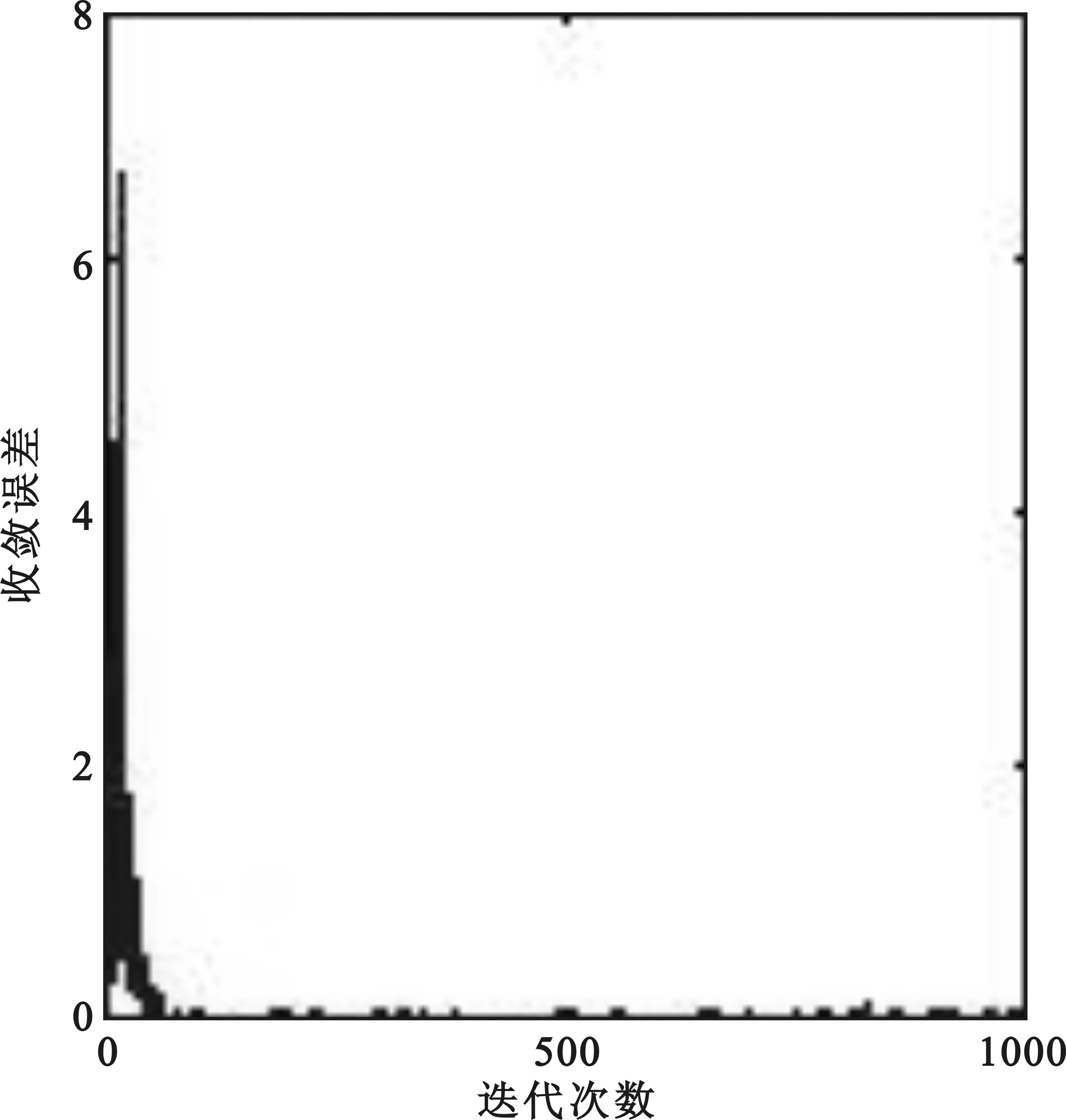
图9 信号输出误差曲线
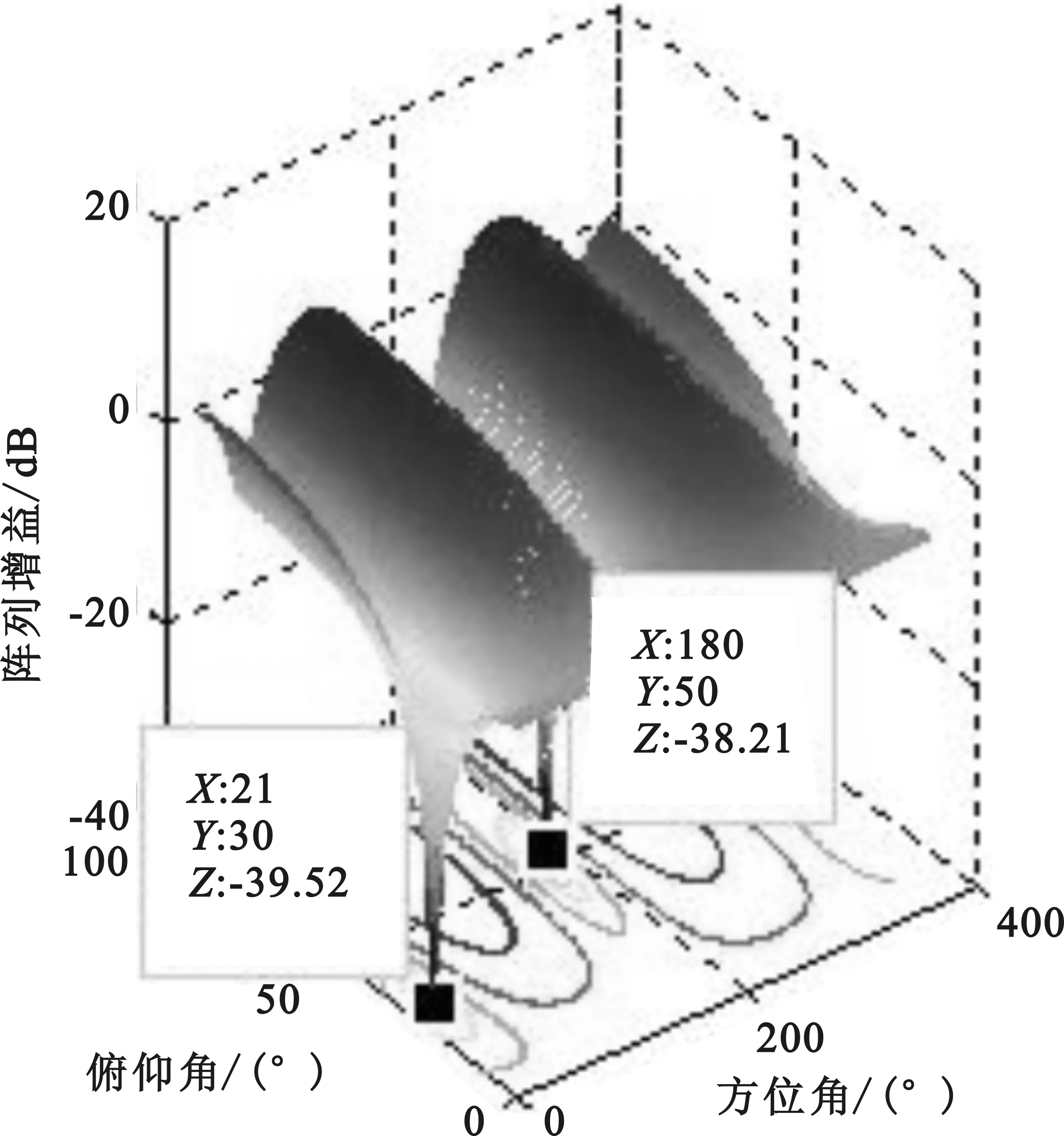
图10 阵列天线方向
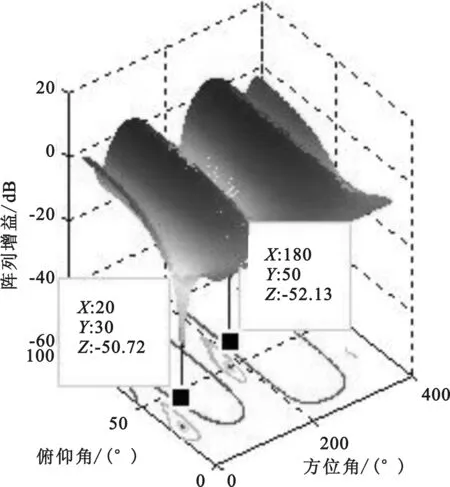
图11 阵列天线方向
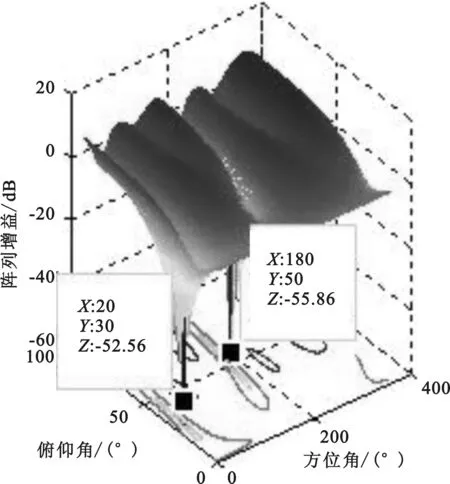
图12 阵列天线方向
从图8、图9中给出的两种算法的收敛曲线可以看出NLMS算法的收敛曲线明显快于LMS算法。
从图10,图11和图12可以看出当增加一个干扰时LMS算法的零陷深度明显变浅,干扰抑制性能下降,但是NLMS算法的零陷深度和多级维纳滤波算法基本抑制,干扰抑制性能基本没有受到影响。
(3)仿真中有三个宽带干扰信号,入射角度分别为(20°,30°),(180°,50°),( 240°,60°),带宽为2 MHz,1.4 MHz和0.8 MHz,干噪比为30 dB。前两个算法收敛情况如图13和图14,三个算法各自的自适应调零天线的方向图如图15,图16和图17所示。

图13 信号输出误差曲线
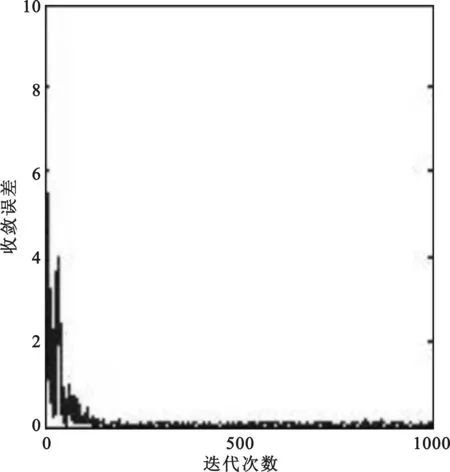
图14 信号输出误差曲线
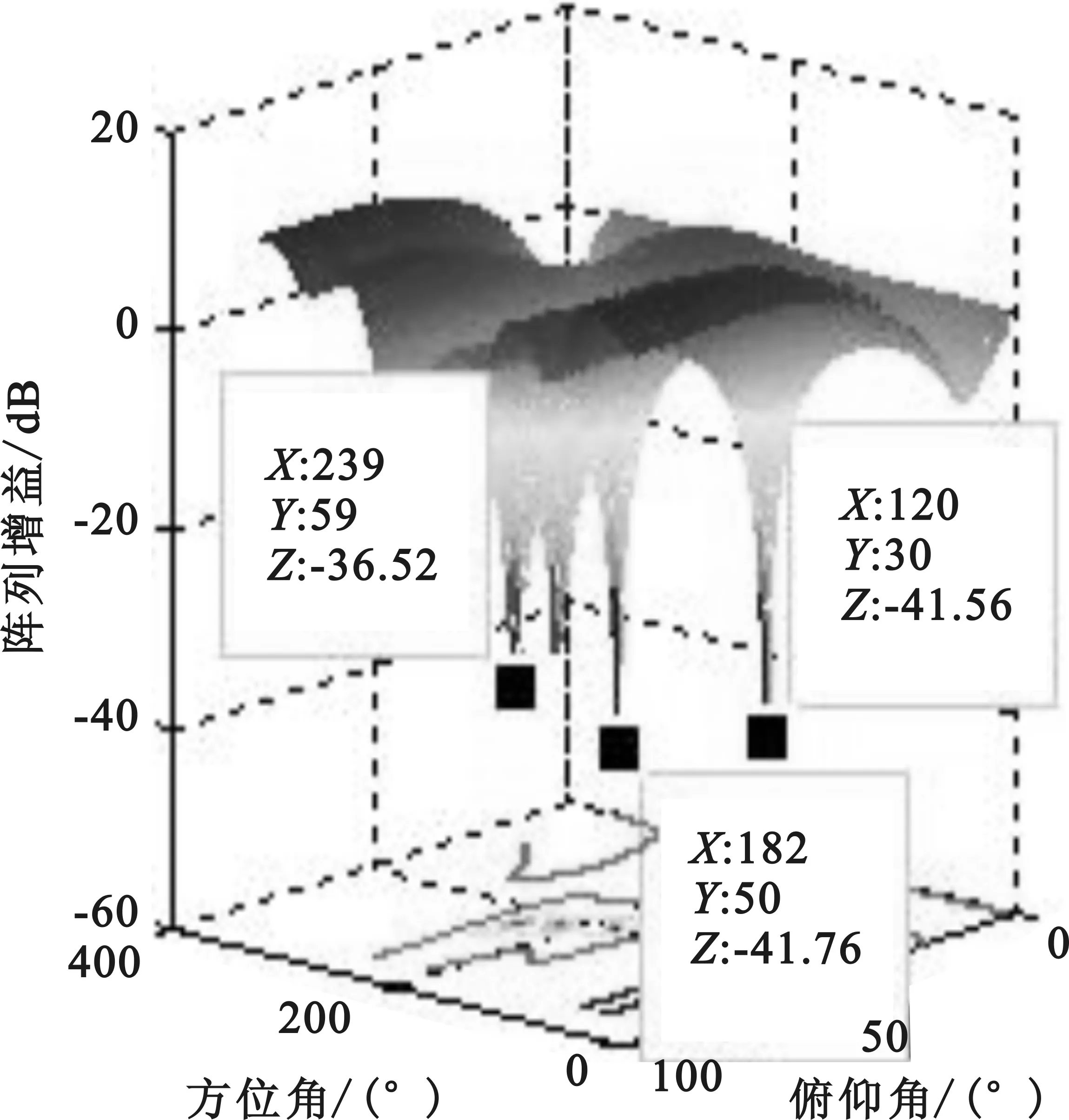
图15 阵列天线方向
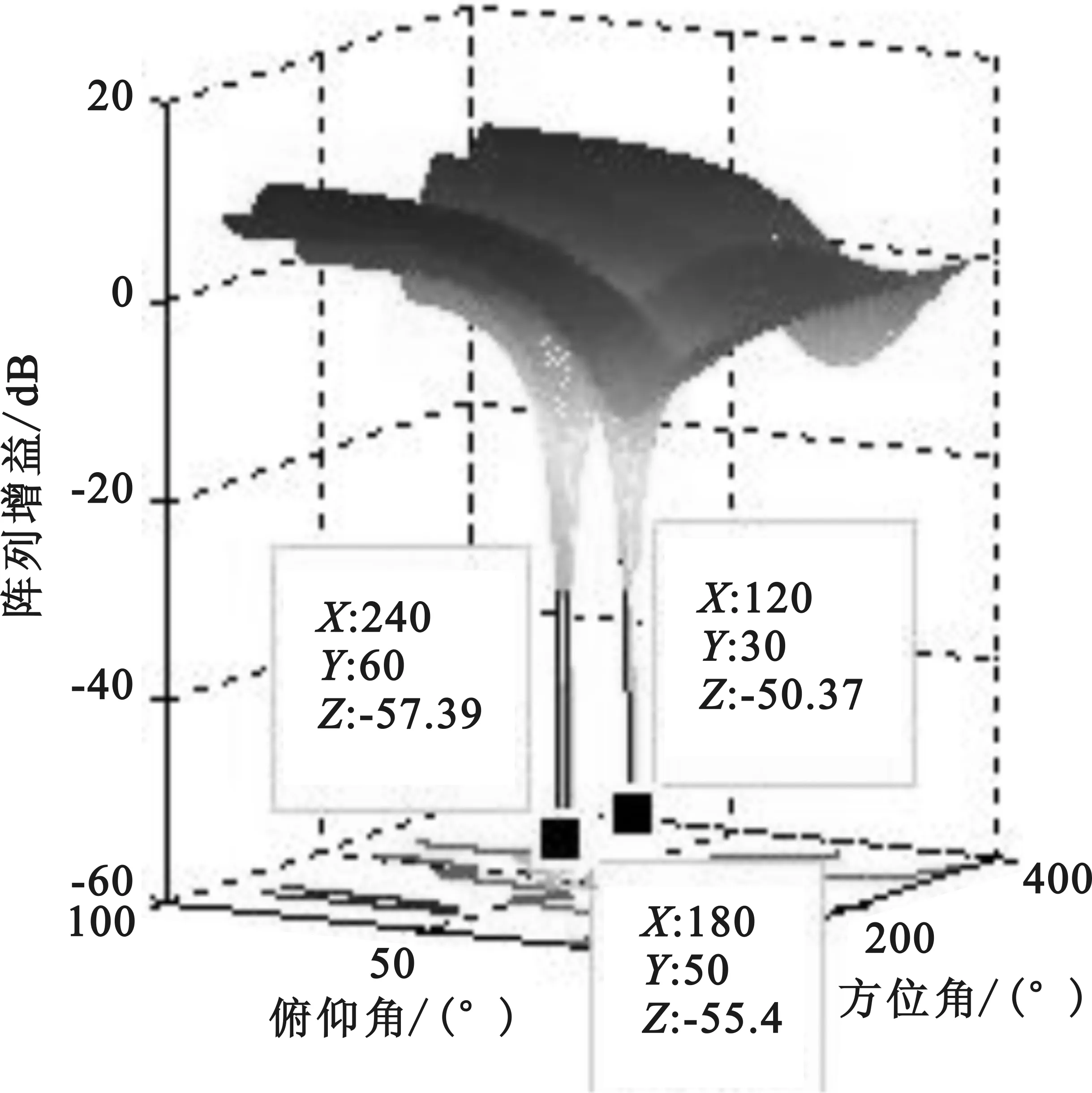
图16 阵列天线方向
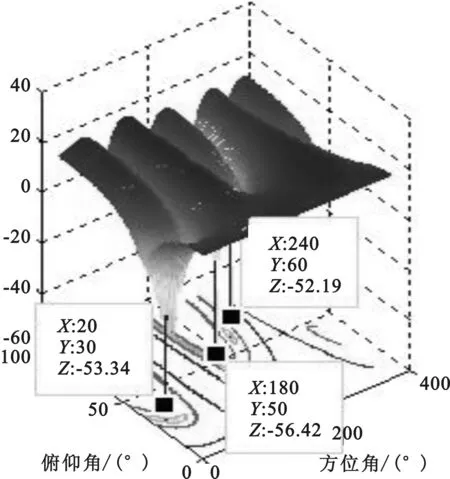
图17 阵列天线方向
从图13和图14可以看出当又增加一个干扰时LMS算法的收敛速度明显变慢,而NLMS算法的收敛速度没有受到影响。此外从方向图上还可以看出NLMS干扰抑制性能没有随着干扰个数的增加而受到影响,从零陷深度来看,NLMS抗干扰算法与多级维纳滤波算法性能相当。
4 结 语
由于空时抗干扰算法中采样数据协方差矩阵维数大,对其求逆很难在工程上实现。目前采用多级维纳滤,LMS等算法来逼近矩阵求逆的结果,但是这两个算法都有其缺点。多级维纳滤波算法计算量大,实时性差,从而影响了其实用性。虽然LMS算法计算量小,权值更新快,但是它的干扰抑制性能差。针对以上情况,本文提出一种变步长的自适应处理算法,此算法是基于功率倒置算法原理的基础上得到的。仿真结果验证了该算法具有收敛性能好、收敛速度快、自适应权矢量的更新速度快、计算量低等优点,并且当干扰个数增加时此算法的性能并没有下降,同样可达到与多级维纳滤波[5]算法相同的性能,但是却避免了多级维纳滤波算法复杂的运算和实时性差的问题。
[1] 向敏,胡飞,周军. 基于变换域选择的干扰抑制技术[J]. 通信技术, 2014, 47(04):377-381. XIANG Min,HU Fei,ZHOU Jun.Interference Suppression Technique based on Transform Domain Selection[J].Communications Technology,2014,47(04):377-381.
[2] 张波,毛良明. 组合扩频信号设计及抗干扰处理方法[J].通信技术, 2012, 45(02):59-64. ZHANG Bo, MAO Liang-ming.Hybird DS/FH TT&C Signal Design and Anti-jimming Technology.Communications Technology,2012,45(02):59-64.
[3] 廖群,郑建生,黄超. GPS自适应抗干扰算法及其FPGA实现[J]. 现代雷达, 2006, 28(04):79-81. LIAO Qun, ZHENG Jian-sheng, HUANG Chao.Realization of GPS Adaptive Anti-jamming Algorithm on FPGA[J]. Modern Radar,2006,28(04):79-81.
[4] ComptonRT. The Power-inversion Adaptive Array: Concept and Performance[J]. IEEE Trans. on AES, 1979, 15(06): 803-814.
[5] J.Scott Goldstein, Irving S.Reed, Louis L.Scharf. A Multistage Representation of the Wiener Filter based on Orthogonal Projection[J]. IEEE Trans. on Information theory, 1998, 44(07): 2943-2959.
DONG Li-mei(1982-), female, M.Sci., engineer,mainly engaged in satellite navigation receiver anti-jamming process.
Application of NLMS Algorithm in GPS Space-Time Adaptive Processing
DONG Li-mei
(Chengdu Spaceon Technology Company , Chengdu Sichuan 610041, China)
By using GPS two-dimention STAP (Space-Time Adaptive Processing) algorithm, the intensity of strong interference and multipath interference can be restrained down close to the noise floor without producing serious loss or distortion of GPS signals. Experiment shows that it enjoys a better anti-jamming capability than space filtering algorithm. However STAP algorithm due to the large dimension of a sample data covariance matrix, thus is much higher than pure space filtering algorithm in computing amplexity,thus is difficult to achieve real-time processing. In light of this, LMS (Least Mean Square) algorithm is commonly used in current projects. Through the analysis of PI (power inversion) algorithm, a variable step-size NLMS( Normalnized Least Mean Square) algorithm is proposed. Inteference supression performance of this algorithm is better than that of LMS, and near to the result of MSWF (Multistage Winer Filter), thus it fairly satisfy the needs of projects for its lower computing complexity, shorter operation time, better feasibility and pracaticability. Simulation comparison of NLMS, LMS and MSWF algorithms indicates that NLMS algorithm is feasible.
space filtering; anti-interference; LMS; MSWF
date:2014-10-08;Revised date:2015-01-20
TN91
A
1002-0802(2015)03-0295-07

董李梅(1982—),女,硕士,工程师,主要研究方向为卫星导航接收机抗干扰处理。
10.3969/j.issn.1002-0802.2015.03.010
2014-10-08;
2015-01-20
