多径衰落信道下的OFDM时频联合同步算法*

2015-06-23熊春林魏急波

通信技术 2015年4期

关键词：度量载波信道

刘晶，熊春林，魏急波

(国防科学技术大学电子科学与工程学院通信工程系，湖南，长沙 410073)

多径衰落信道下的OFDM时频联合同步算法*

刘晶，熊春林，魏急波

(国防科学技术大学电子科学与工程学院通信工程系，湖南，长沙 410073)

符号定时和载波频率偏差将严重影响OFDM系统的性能。基于具有重复结构的CAZAC序列，提出了一种仅利用一个CAZAC符号实现符号定时、整数倍频偏与小数倍频偏估计的同步算法。这种算法在完成粗定时同步的同时得到整数倍频偏估计，然后根据整数倍频偏估计值对定时估计进行修正，最后完成小数倍频偏估计。分析与仿真结果表明，该算法相对经典算法，不但提高了传输效率，还显著改善了OFDM系统的定时与频偏估计性能，相比CAZAC序列算法，提升了多径信道下的同步性能。

正交频分复用；符号定时偏差；载波频率偏差；多径衰落信道

0 引言

正交频分复用技术(Orthogonal Frequency Division Multiplexing，OFDM)是WLAN、4G-LTE[1]等宽带无线通信系统的物理层核心技术之一。OFDM技术具有抗频率选择性衰落、频谱利用率高和抗窄带干扰的优点，但是对符号定时和载波频率偏差比较敏感。在宽带无线通信系统中，符号定时和载波频率偏差将引入符号间干扰(Inter Symbol Interference，ISI)和子载波间干扰(Inter Carrier Interference，ICI)，导致系统性能急剧下降。因此，进行精确的时偏和频偏估计与补偿显得尤为重要。

针对OFDM时偏和频偏估计问题，近年来进行了广泛深入地研究，提出了多种估计算法[2-8]。文献[2]提出利用两个相同训练序列估计频偏的频域同步算法，频偏估计精度高，但估计范围不大于0.5个子载波间隔。文献[3]研究了基于PN序列的时频同步算法，该算法能较精确地估计出小数倍和整数倍频偏，但是由于度量函数存在“峰值平台”，其定时同步的性能较差。在文献[3]的基础上，文献[4]通过对循环前缀内的定时度量取算数平均来完成定时同步，一定程度上改善了定时估计性能。文献[5]则通过构造具有对称结构的训练序列，使得定时度量函数变得尖锐，有效提升了定时估计性能，但是该算法无法估计频偏。文献[6]利用两个OFDM符号长度的训练序列进行同步，获得了较好的性能，但是增加了系统开销。文献[7]利用循环前缀完成同步，但估计精度不高。文献[8]整数倍频偏估计在频域完成，但是定时同步与小数倍频偏需要通过其它算法获取。由上可知，已有算法难以兼顾符号定时、小数频偏与整数频偏三者的估计性能。

针对上述问题，本文提出仅利用一个CAZAC(Constant Amplitude Zero Auto-Correlation，CAZAC)符号实现符号定时、整数倍频偏与小数倍频偏联合估计的OFDM同步算法。该算法充分利用CAZAC序列良好的互相关和自相关特性，从尖锐的度量函数中得到精确的定时估计。然后利用时域CAZAC序列在整数倍频偏下的移位特性估计出整数倍频偏，并进一步修正定时估计结果。最后，完成小数倍频偏估计。所提算法既降低了系统的开销，同时还兼顾了时偏和频偏估计性能。

1 系统模型

OFDM系统模型如图1所示，发送数据经过信道编码，QAM映射，IFFT和加CP等处理后得到OFDM信号，再经过无线信道传输。在接收端，先对接收信号进行同步处理，估计并补偿符号定时和载波频率偏差，才能保证后续QAM解映射和信道解码等处理的正确进行。

假设N为OFDM的IFFT(FFT)点数，Nu为非虚子载波个数(Nu≤N)。在每个OFDM符号前加入长度为NG的循环前缀。X(k)表示调制在第k个子载波上的频域符号。那么，发送端基带OFDM时域采样信号x(n)可以表示为：

(1)

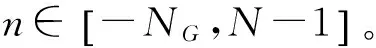
(2)

其中，L为路径数，h1为第l条路径对应的复增益，τl为第l跳路径对应的时延。

发射信号经过多径衰落信道后，接收端得到的时域采样信号r(n)为：

(3)

图1 OFDM系统收发端模型

研究表明，在宽带无线通信系统中，定时和频率偏差会引起ISI和ICI，严重影响系统性能。文献[2][10]研究指出，为了保证OFDM系统性能，在AWGN信道中，残余频偏应小于子载波间隔的4%；而在多径衰落信道中，则应小于子载波间隔的2%。在实际系统中，频偏通常可以达到数倍子载波间隔以上，时偏也会超过系统的可容忍范围。因此，OFDM接收机需要完成较精确的定时与频率估计。下面分别对所提OFDM同步算法的各个组成部分进行详细描述。

2 OFDM定时与频偏估计算法

基于数据辅助类同步算法思想，本文从CAZAC序列出发，提出了一种新的OFDM时偏和频偏估计算法。

2.1 训练序列结构

(4)

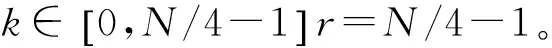
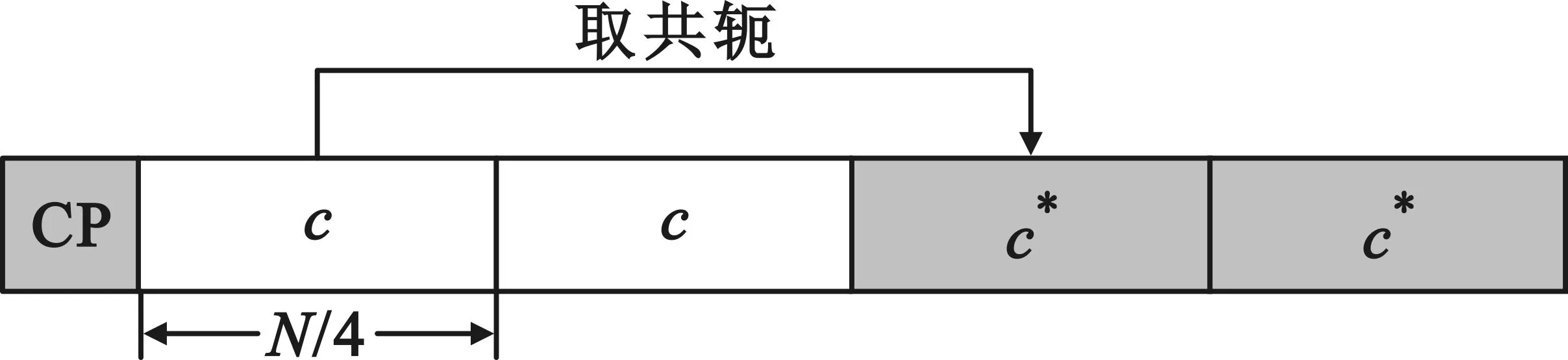
图2 训练序列结果示意

2.2 定时同步

定时同步的性能与定时度量函数密切相关。文献[9]指出，定时度量函数越尖锐，越有助于提升定时同步性能。针对图2中的训练序列，利用本地序列c与接收信号r进行互相关作为定时度量函数。那么，度量函数Λ(d)为：

(5)

由式(5)得到的定时估计为：

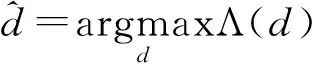
(6)

2.3 整数倍频偏估计

针对图2所示的训练序列，下面分析整数倍频偏εi对序列c的影响。假设不考虑多径信道和噪声的影响，部分训练序列c仅受到整数倍频偏εi影响得到序列c′，则c′的第k个元素c′(k)为：

(7)

由上述证明可得，在整数倍频偏εi的影响下，长度N/4的序列c和c*分别向左右方向各循环移动εi/4位。整数倍频偏估计正是利用此性质完成的。

图3 整数倍频偏估计示意图

利用本地序列c和c*与接收信号r进行互相关，得到定时度量函数分别为：

(8)

(9)

(10)

(11)

利用式(11)的整数倍频偏估计值修正式(6)的定时估计为:

(12)

2.4 小数倍频偏估计

由式(12)得到修正的定时估计值后，利用训练序列的重复特性完成小数倍频偏估计。小数倍频偏估计值为:

(13)

综上所述，本文所提算法根据图2所示的训练序列结构，设计基于互相关的度量函数，分别得到定时估计、整数倍频偏和小数倍频偏估计。

3 仿真结果与分析

本节分别在高斯信道和多径衰落信道(ITU-VA，ITU-PB)[13]下验证所提同步算法性能，并与经典的时频同步算法[3]、文献[6]和[8]中的算法进行比较。主要仿真参数如表1所示。

表1 仿真参数设置

在发送信号前加入固定长度的噪声信号来模拟接收端未知定时位置。设置频偏为ε=100.25，整数倍频偏为εi=100，小数倍频偏为εf=0.25。

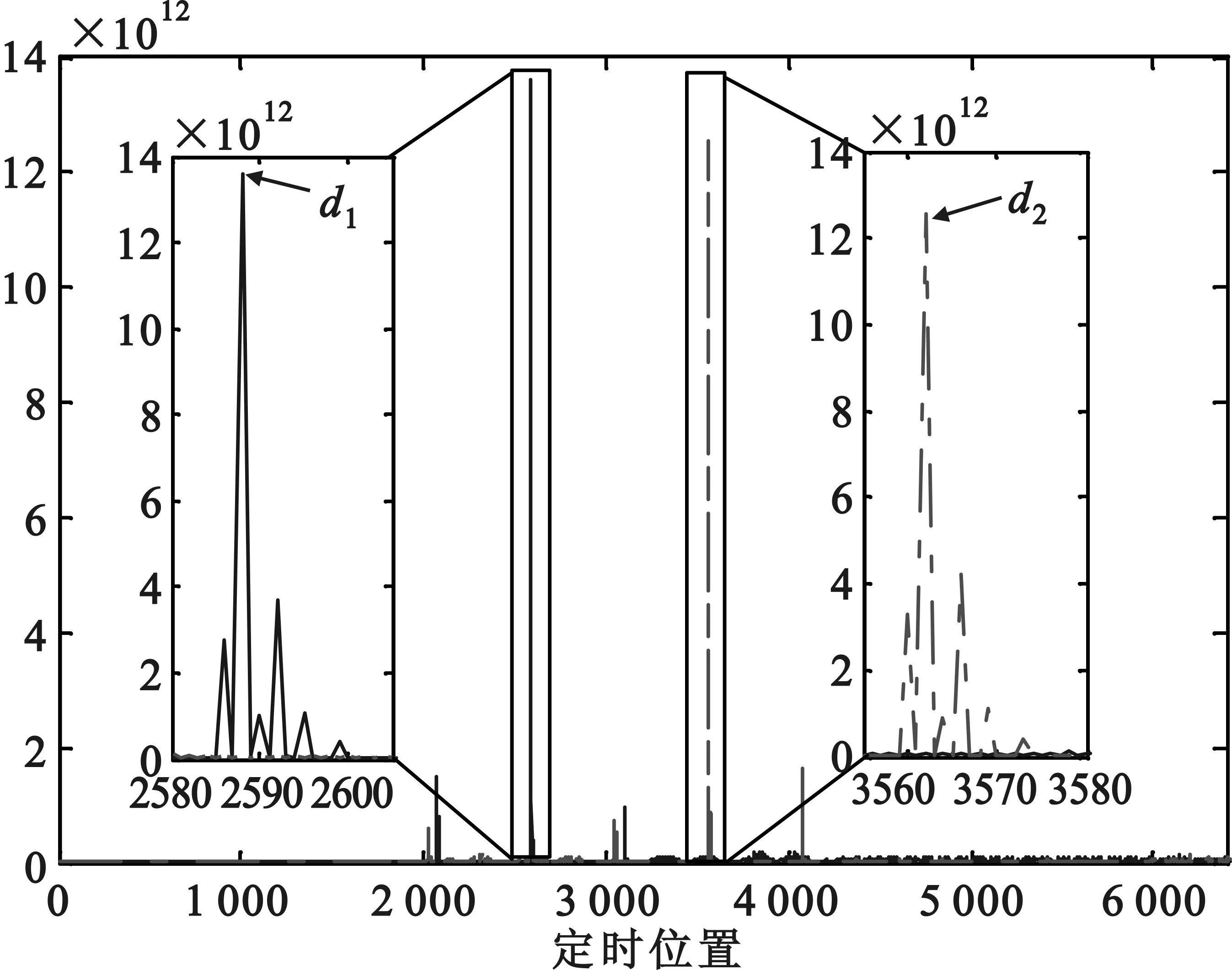
图4 VA信道下定时度量函数曲线

图5 整数倍频偏估计性能曲线

图4为多径信道(ITU-VA)下的度量函数曲线。传统SC算法度量函数存在“峰值平台”[3]，而图4中的度量函数比较尖锐，有助于提高定时估计性能。由于多径衰落信道的影响，使得定时度量函数存在多个峰值，但主径(能量最大的路径)上的相关峰值远大于其他径，大大降低了误定时同步的发生。图5为整数倍频偏捕获性能曲线。由图5可得，在高信噪比时，本文算法与SC算法、文献[8]算法捕获概率均趋近于1。而在低信噪比时，所提算法捕获概率远高于SC算法。此外，所提算法仅利用图2所示的一个训练符号完成整数倍频偏估计，相比于传统SC算法需要两个符号的训练序列，本文算法提高了系统传输效率。文献[8]算法的估计性能略高于所提算法，但文献[8]算法是在假设理想时间同步条件下，估计整数倍频偏。OFDM同步的研究是不能离开定时同步进行的，定时同步要先于频偏估计完成的，若定时都不能获得，往往也不能获得整数倍频偏估计。而且，文献[8]算法是在频域完成估计，频域算法需要进行FFT运算，需要延迟比较大。

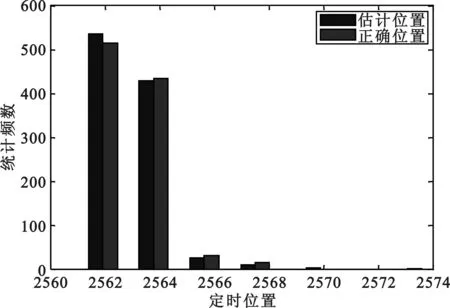
图6 VA信道下定时位置分布图

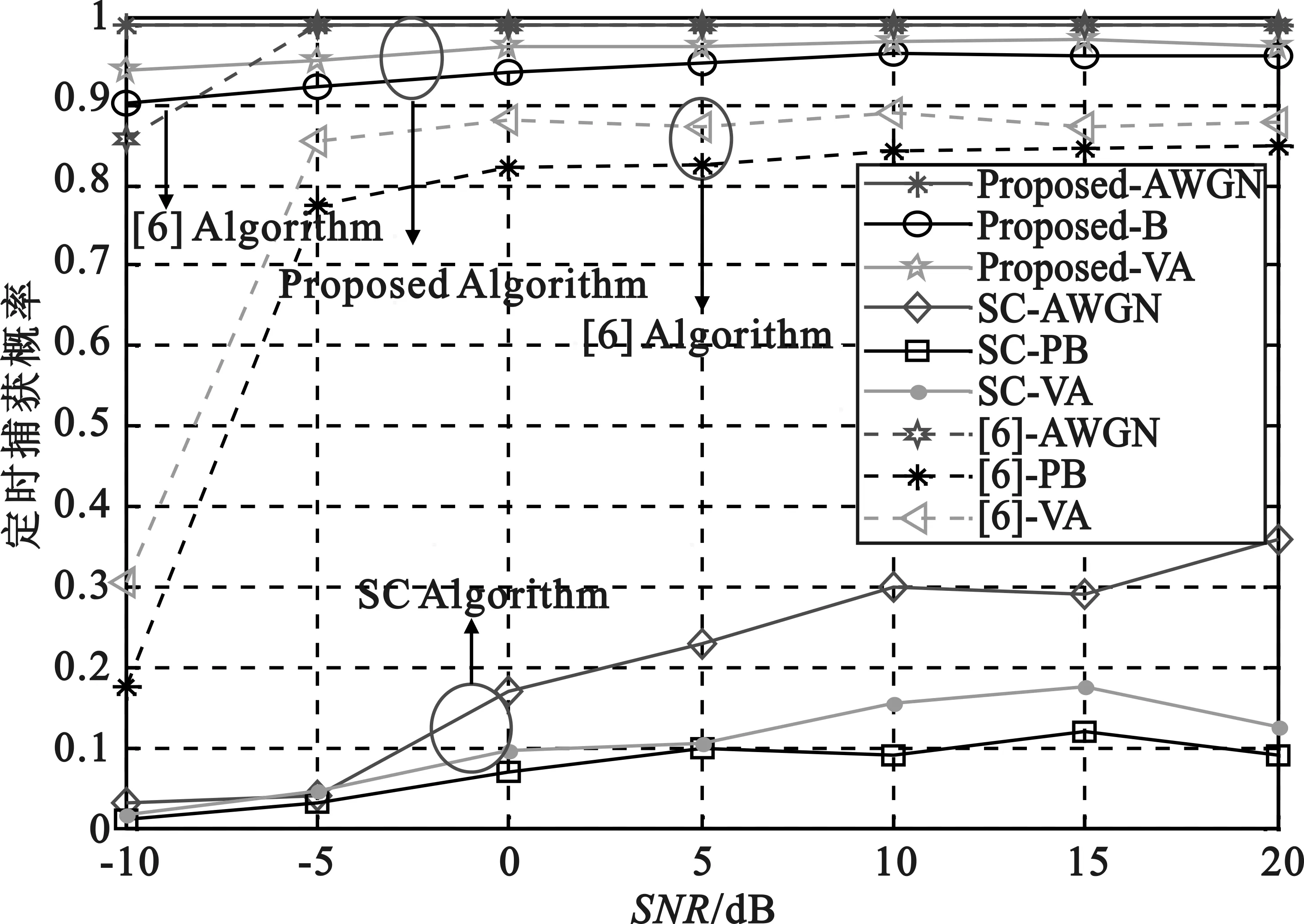
图7 定时捕获概率性能曲线

图6为ITU-VA信道下的1 000次仿真中，正确定时位置与所提算法估计的定时位置统计对比图，其正确定时位置对应当前多径信道下的主径。从图6可以看出，在多径信道下，所提算法的定时同步性能较高。图7为算法在三种信道下的定时捕获性能曲线。从图7可以看出，所提算法定时捕获概率高于传统SC算法和文献[6]算法。此外，在多径衰落信道下，本文算法定时捕获概率仍大于90%，且高于SC算法和文献[6]算法。因此，所提算法更适用于多径衰落信道。

图8和图9分别给出了算法的小数倍频偏估计均值和方差随SNR变化的性能曲线。从图8可以看出，在三种信道环境下，所提算法小数倍频偏估计均值非常接近真实值，且在低信噪比时估计性能显著优于传统SC算法和文献[6]算法。从图9可以看出，在SNR大于5dB时，该算法频偏估计方差达到10-4数量级，满足OFDM系统对残余频偏不大于子载波间隔的2%的要求[9]，并且性能优于传统SC算法。在AWGN信道下，[6]算法的估计方差小于所提算法，但在多径信道下，[6]算法的估计方差远远大于所提算法，进一步说明了所提同步算法对多径信道的良好适应性。

4 结语

在OFDM系统中，符号定时和载波频率偏差将严重影响系统性能。本文基于CAZAC序列，提出了一种新的OFDM定时与频偏同步算法。不同于文献[8]算法在频域进行估计，这种算法的定时估计、小数倍频偏和整数倍频偏估计均在时域完成。这种算法仅利用一个符号长度的CAZAC序列完成同步，相比于经典同步算法[3]，提高了系统传输效率，有利于实际应用。分析和仿真结果表明，在多径信道下，所提同步算法相对于经典SC同步算法和现有利用CAZAC序列的同步算法[6][8]，显著提升了估计性能，更适用于实际环境。后续可结合频偏补偿进行进一步研究。

[1] 3GPP TS 36.211 v12.3.0, 3rd Generation Partnership Project; Technical Specification Group Radio Access Network; Evolved Universal Terrestrial Radio Access (E-UTRA); Physical Channels and Modulation (Release 12), 2014.

[2] Moose P H. A Technique for Orthogonal Frequency Division Multiplexing Frequency Offset Correction [J]. IEEE Transactions on Communications,1994,42(10):2908-2914.

[3] Schmidl T M, Cox D C. Robust Frequency and Timing Synchronization for OFDM [J]. IEEE Transactions on Communications, 1997, 45(7): 1800-1805.

[4] Minn H, Zeng M, Bhargava V K. On Timing Offset Estimation for OFDM Systems [J]. IEEE Communications Letters, 2000, 4(7)：242-244.

[5] Park B, Cheon H, Kang C, et al.A Novel Timing Estimation Method for OFDM Systems [J].IEEE Communications Letters, 2003, 7(5): 239-241.

[6] 朱彦，张会生，骆艳卜. 基于CAZAC序列的OFDM时频同步算法 [J]. 计算机仿真. 2009, 26(11): 130-133. ZHU Yan, ZHANG Hui-sheng, LUO Yan-bo. An OFDM Timing and Frequency Synchronization Algorithm Based on CAZAC Sequence [J]. Computer Simulation, 2009, 26(11): 130-133.

[7] 张子文.基于最大似然算法的OFDM同步技术研究 [J]. 通信技术. 2010, 43(5): 16-18. ZHANG Zi-wen. OFDM Synchronization Technologies based on Maximum Likelihood Estimation Algorithm [J]. Communication Technology. 2010, 43(5): 16-18.

[8] 严春林，李少谦，唐友喜等. 利用CAZAC序列的OFDM频率同步方法 [J]. 电子与信息学报. 2006, 28(1): 139-142. YAN Chun-lin, LI Shao-qian, TANG You-xi, et al. New Frequency Offset Estimation Methods for OFDM Systems by Using CAZAC Sequence [J]. Journal of Electronics & Information Technology. 2006, 28(1): 139-142.

[9] YANG F, ZHANG X. Sharpening Timing-Metrics for Auto-Correlation Based Coarse Symbol Synchronization in OFDM Systems [C] // Communications (ICC), 2014 IEEE International Conference on. IEEE, 2014: 2227-2232.

[10] Van de Beek J J, Sandell M, Brjesson P O. ML Estimation of Timing and Frequency Offset in OFDM Systems [J]. IEEE Transactions on Signal Processing, 1997, 45(7): 1800-1805.

[11] Bomer L, Antweiler M. Perfect N-phase Sequences and Arrays [J]. IEEE Journal on Selected Areas Communications, 1992, 10(4): 782-789.

[12] David C Chu.Ployphase Codes with Good Periodic Correlation Properities [J].IEEE Transactions on Information Theory, 1972,18(4): 531-532.

[13] Recommendation ITU-R M.1225, Guidelines for Evaluation of Radio Transmission Technologies for IMT-2000, 1997.

Timing-and-Frequency Synchronization Algorithm for OFDM Systems in Multipath Fading Channels

LIU Jing, XIONG Chun-lin, WEI Ji-bo

(Department of Communication Engineering, College of Electronic Science and Engineering, NUDT, Changsha Hunan 410073, China)

Symbol timing offset and carrier frequency offset would seriously deteriorate the performance of OFDM system. Based on the CAZAC sequences with repetitive structure, a novel synchronization algorithm is proposed,which uses merely one CAZAC symbol to realize the synchronization of symbol timing offset, integer frequency offset and fractional frequency offset. Firstly, the proposed algorithm completes the coarse timing synchronization while obtaining integer frequency offset estimation. Then, the timing offset estimation is correted in accordance with the integer frequency offset estimation. Finally the estimation of fractional frequency offset is done in the final process. Analysis and simulation results indicate that compared with classical synchronization algorithm, the proposed algorithm could increase the transmission efficiency and significantly improve the estimation performance of timing offset and frequency offset for OFDM system. Meanwhile, the synchronization performance in multipath channels is enhanced as compared with CAZAC sequence algorithm.

OFDM; symbol timing offset; carrier frequency offset; multipath fading channels

date:2015-01-06；Revised date：2015-03-19

TN92

1002-0802(2015)04-0386-06