我国房地产指数收益率的波动性研究

大量的实证研究表明，由于存在许多不可知因素的影响，时间序列数据的随机波动性是不可预测的。但又由于这类数据的异方差特性，可以利用时间序列处理技术对其较为准确的预测，使得对时间序列数据的随机波动性得到控制。1982年恩格尔提出的ARCH模型并由伯勒斯莱文发展为GARCH模型就是一个重要的时间序列处理技术。之后又有一些学者将这类模型进行了拓展与应用，使其成为分析金融时序数据的波动性与收益性的重要工具之一。

ARCH类模型在金融时序数据的波动性中具有很好的效果。赵士玲、张能福（2011）曾用ARCH类模型对我国的上证指数进行实证研究，秦晓宇（2012）也曾用GARCH模型对深证成指的收益率进行了波动性研究。他们利用ARCH类模型都准确地描述了我国股市上的各指数收益率的波动特征，但是对于研究房地产指数收益率的波动性研究的文章却少之又少。因此笔者在本文利用三种ARCH类模型对我国房地产指数的收益率进行波动性研究，找出能最好拟合我国房地产指数收益率波动性特征的模型，并且得出相应的结论。

一、ARCH类模型简介

（一）ARCH模型

自回归条件异方差（ARCH）模型是最简单的条件异方差模型，该模型假定了随机误差项的条件方差与其误差项滞后的平方有关。由两个方程组成：方程（1）为均值方程，其中是被解释变量，是

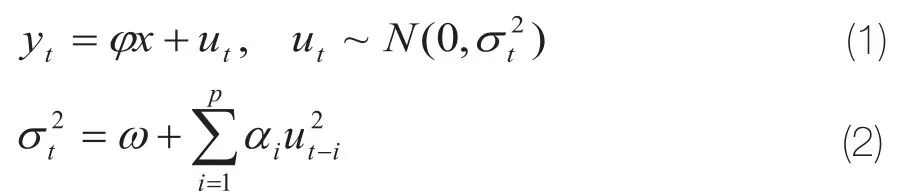
解释变量。方程（2）成为方差方程，其中是的条件方差。

（二）GARCH模型

当发现金融时序数据存在ARCH效应后，相对应建立的ARCH(p)模型在回归估计中，往往需要很多的滞后期数才能得到较好的拟合效果，因此在使用此模型时，就不可避免地需要估计更多的参数。于是伯勒斯莱文于1986年在ARCH(p)模型的方差方程中增加了q个自回归项，建立了GARCH模型，对应的方差方程如下：

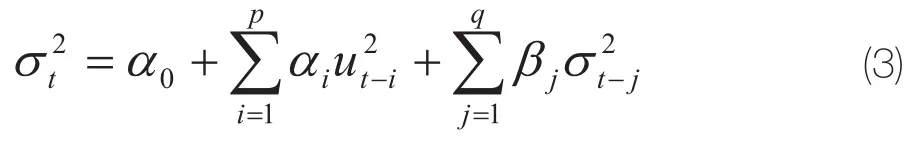
其中p是ARCH项的阶数，q是GARCH项的阶数。

GARCH模型将被解释变量的波动分解了自身过去的冲击和外生变量的冲击，其中参数分别代表这两部分冲击作用的强度。GARCH模型除了对误差的条件异方差问题处理更加合理外，还对被解释变量的方差进行更加有力的描述或预测，使其成为投资者衡量所持有资产的风险和期权定价的有力工具。

（三）TGARCH模型

在金融市场上，金融资产收益率的条件异方差经常会表现出对正负的未预期到收益的反应并不相同的情况。由于这种条件异方差的不对称性，需要引入非对称性的GARCH模型来处理这类问题，TGARCH模型就是其中的一种。它引入虚拟变量来设定一个门限，用来区分正和负的冲击对条件异方差的影响，其对应的方差等式为：

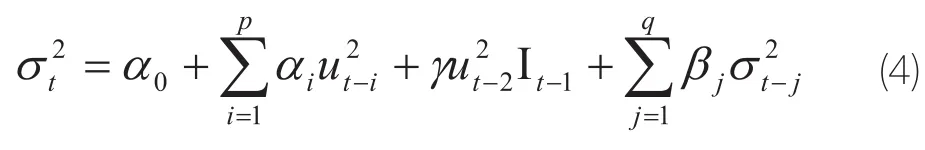
（四）EGARCH模型

EGARCH模型又称指数GARCH模型，是由纳尔什提出，也是一种反应条件异方差不对称性的模型，其条件方差以对数的形式表示：

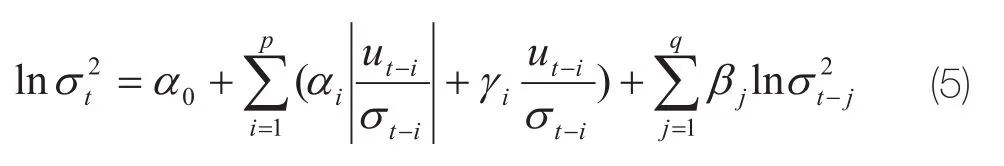
其方差等式分析的是分别使用均值等式的扰动项和扰动项的绝对值与扰动项的标准差之比来捕捉正负冲击对波动性的影响。

二、实证分析

本文以房地产指数的收益率率作为分析对象，样本选取范围为1996年12月26日到2014年9月30日的房地产指数的收盘价指数，共6488个样本数据，数据来源于大智慧软件。其中笔者设为第t日的房地产指数的收盘价。

（一）基本统计分析

根据房地产指数的收盘价数据，对收益率序列进行描述性统计分析，其结果如表1所示。

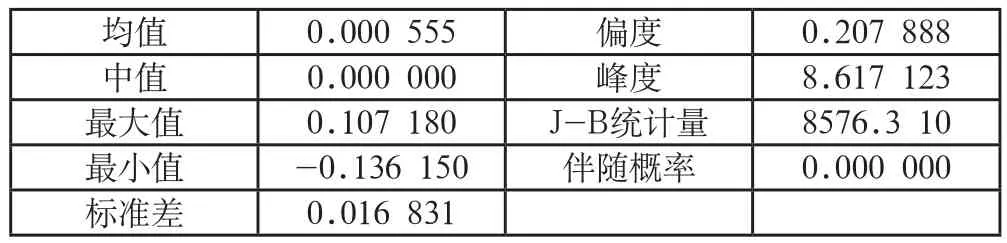
表1 地产指数收益率统计

从表1可以得知，收益率序列rt的偏度系数为0.208，有一定的右偏现象，而峰度系数为8.617，显著大于正态分布的分度系数3，说明序列rt存在明显的尖峰厚尾的特征；J-B统计量与伴随概率的值也充分说明了序列rt拒绝正态分布的假设。

为了避免下文分析过程中出现的伪回归，将收益率序列rt进行ADF单位根检验，检验结果如表2所示。

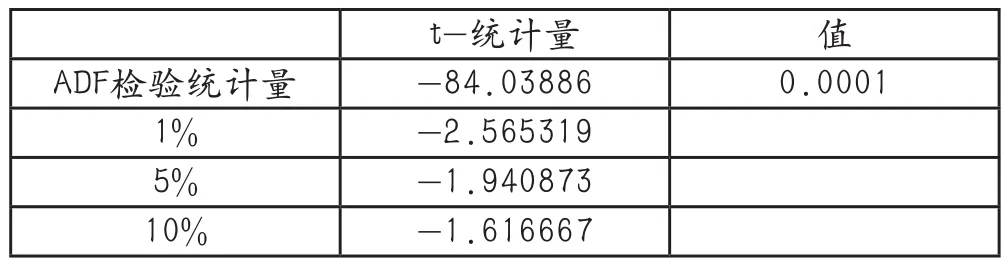
表2 单位根检验结果

从表2数据中可知，ADF检验统计值都小于在1%、5%、10%显著水平下的临界值，因此拒绝原假设，说明收益率序列不存在单位根，是平稳序列，可以直接建模分析。

（二）模型建立

根据房地产指数的收盘价数据，可以作出收益率序列rt的时序图，如图1所示。

从图1中可知，收益率序列表现为一个较大幅度的波动后紧随着另一个大幅度的波动，一个较小幅度的波动后紧随着另一个较小幅度的波动，即波动的集群现象。于是考虑收益率序列是否存在条件异方差，进而使用ARCH类模型对其波动性研究。

通过对收益率序列的自相关图与偏相关图进行相关性分析，可以确定rt序列是一个可以建立AR(3)的自回归模型。通过Eviews7.0软件对上述的数据进行参数估计可以得出表达式为：

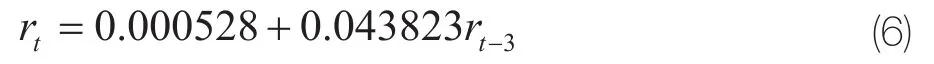
表达式中的模型各参数的统计检验均在5%显著水平下通过。为了验证收益率序列rt是否具有ARCH效应，对此均值方程中的残差序列进行ARCH—LM检验，检验结果如表3。

表3 ARCH-LM检验结果表

表3数据说明模型存在着条件异方差，需要在AR(3)均值方差的基础上建立ARCH类模型来分析收益率的波动性。

（三）模型估计与结果分析

对收益率序列建模rt，基础均值方程为AR(3)模型，在正态分布下，经过对ARCH类模型来描述序列的异方差性，比较分析结果如表4、表5、表6。

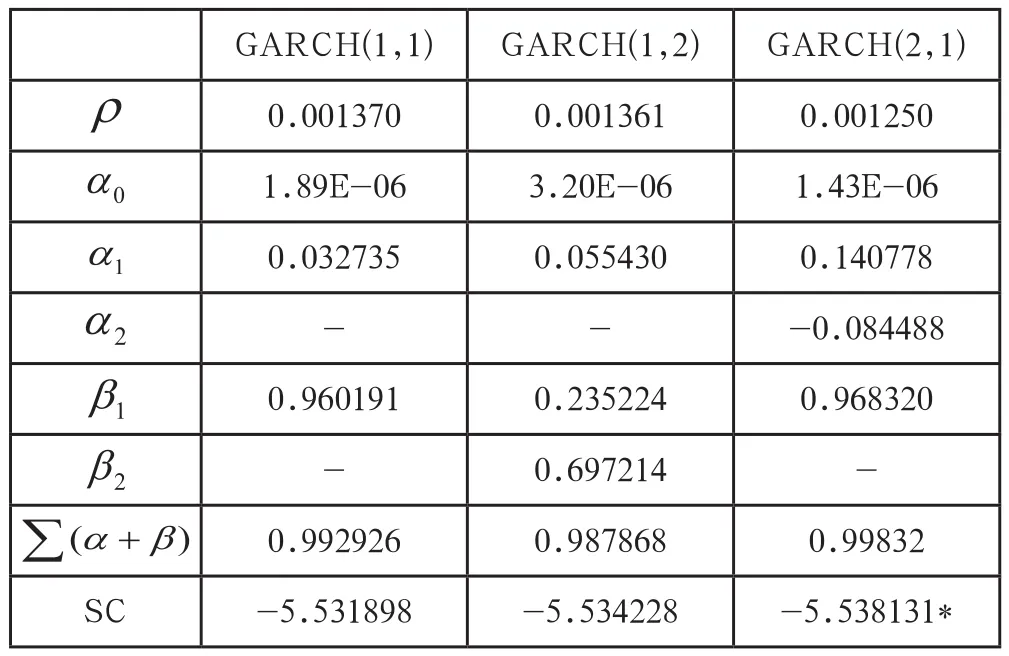
表4 收益率AR(3)-GARCH(p,q)模型方差方程实证结果

表4给出几种拟合收益率波动的GARCH模型的结果。从中由AIC与SC准则可知，GARCH(2,1)模型提供了最佳的拟合，并且该模型的ARCH项和GARCH项的系数，显著差异于零，这表明条件异方差性很强。

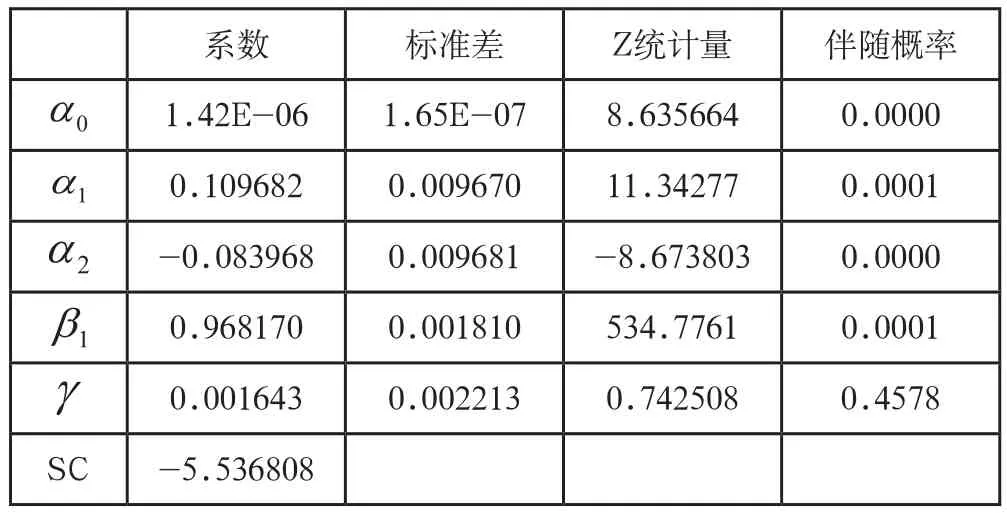
表5 收益率AR(3)-TARCH(2,1)模型方差方程实证结果

由表5中得知，系数不显著，这表明房地产指数的增长率不存在明显的杠杆效应，此时房地产指数受到外部的正负冲击时，对其增长率的波动没有显著的差别。

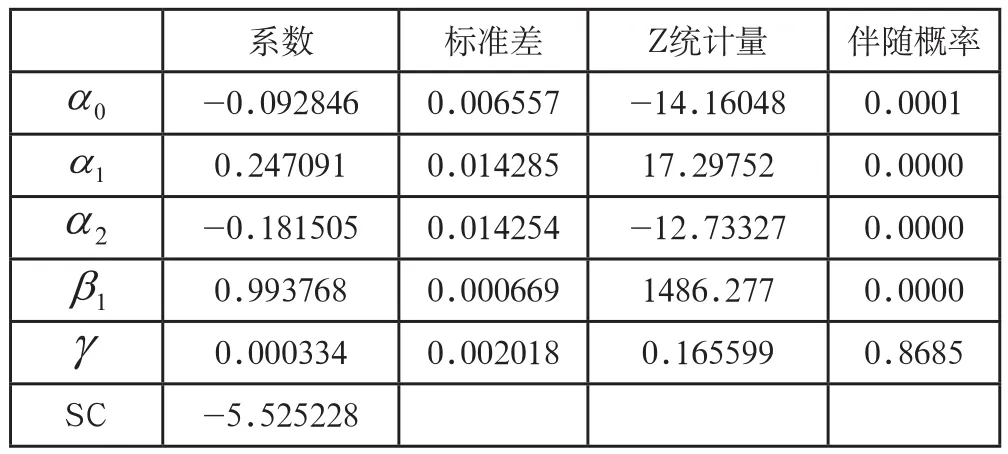
表6 收益率AR(3)-EARCH(2,1)模型方差方程实证结果

由表6中同样得知，系数不显著，这表明房地产指数的增长率不存在明显的杠杆效应，此时房地产指数受到外部的正负冲击时，对其增长率的波动没有显著的差别。

三、结论

笔者通过应用ARCH类模型对我国自涨跌停板以来的房地产指数的收益率进行了波动性研究，结果表明：（1）房地产指数收益率序列存在着显著的异方差性，地产指数价格变动存在明显的“尖峰厚尾”现象；（2）通过对比各类GARCH模型，得出GARCH模型比较显著，而TGARCH和EGARCH模型不显著，即房地产指数的增长率不存在明显的杠杆效应；（3）在GARCH模型中，各ARCH系数与GARCH系数之和非常接近1，这表明地产指数收益率波动存在较强的持续性效果。

[1]李嫣怡,刘荣.Eviews统计分析与应用(修订版)[M].北京:电子工业出版社,2013.

[2]赵士玲,张能福.我国上证指数ARCH效应的实证研究[J].科技创业月刊,2011(7).37-38.

[3]秦晓宇,王悠萍.基于GARCH模型的深证成指收益率波动性研究[J].现代物业,2012(3).70-73.

[4]斯托克.计量经济学(第二版)[M].上海:格致出版社.2009.

[5]季美峰,王军.深市沪市地产股指数收益率波动性的统计研究[J].统计研究,2007(8).57-59.

[6]陆红.基于VaR-GARCH族模型的我国商业银行汇率风险度量研究[D].沈阳:东北大学,2010.