自适应堆栈滤波在极化SAR图像分类预处理中的应用

白 桦,冯恩信

(1.西安交通大学 电子信息与信息工程学院,陕西西安 710049；2.63898部队,河南济源 454001)

工程与应用

自适应堆栈滤波在极化SAR图像分类预处理中的应用

白 桦1,2,冯恩信1

(1.西安交通大学 电子信息与信息工程学院,陕西西安 710049；2.63898部队,河南济源 454001)

堆栈滤波器属于非线性滤波器的一种,它在滤波后图像的边缘和细节保持方面有很好的效果。研究将自适应堆栈滤波器引入到对极化合成孔径雷达(pol-SAR)图像分类的预处理,即滤除极化SAR图像相干斑噪声。而递归过程在平均绝对误差(MAE)准则下对堆栈滤波器的优化也在缩短滤波程序执行时间和强化输出图像质量方面都有不错的效果。滤波后的图像将会首先进行相干数据分解(H/A/α分解),基于分解后的数据使用H-α/Wishart分类方法来进行极化SAR图像分类,分类效果将会与基于其他滤波预处理后的分类图像进行比较并得出最后结论。

堆栈滤波；图像分类；pol-SAR；H-α/Wishart分类

0 引 言

近年来，随着极化合成孔径雷达（polarmetric Synthetic Aperture Radar，极化SAR）成像技术的发展与广泛应用，如何在极化SAR图像分类的预处理中滤除其本身固有的相干斑噪声成为了极化SAR图像处理的重要课题。堆栈滤波器是一种非线性滤波器，对于处理相干斑这种乘性噪声有其先天的优势。由于其具有的并行结构，主要的滤波工作在二进制域进行，实现简单，从而更加方便集成应用。而从实现域角度来看，堆栈滤波器在保存图像纹理和细节方面都有很好的效果[1]。AKOPIAN[1]对堆栈滤波处理过程有着较为全面的论述，LIN Yin[2]等又在此基础上提出了堆栈滤波的自适应方法来进行图像处理，María Elena Buemi[3]等又将自适应堆栈滤波方法引入到SAR图像处理上。研究将自适应堆栈方法进行改进后应用在极化SAR相干斑滤波中，并将处理后的数据进行图像极化分解并进行无监督分类，并与其它的图像滤波方法和其对应的无监督分类方法进行对照和比较。

1 适应堆栈滤波器的算法与实现

1.1 堆栈滤波器设计思路

研究选取的Pol-SAR图像数据为四极化Stockes矩阵数据格式，必须将其转化为极化协方差矩阵以后才能转化为图像并进行预处理。然后根据Lee等关于极化SAR相干斑滤波需遵循的准则[4]，为了保持散射特征、边缘清晰度和单一散射目标特征，滤波器应能自适应地选取或加权邻近的像素。在此基础上为了保持极化数据的可靠性，设计滤波器的思路应注意以下几点:1、对协方差矩阵的合理估计；2、代入模型区域的合理分布；3、最优解和滤波窗口的选定。研究采取的相干斑噪声模型为乘积模型，由于同极化和交叉极化去相关的假设，协方差矩阵可以简化[3-4]；在模型区域处理中，我们预假设窗口区域为均匀，在其中心窗中取均值作为先验均值，经过平均绝对误差（MAE）准则[5-6]判定，满足阈值条件后进行滤波；而堆栈滤波器又由正布尔函数定义，因此研究堆栈滤波器的最优解和窗口的问题都要首先确定其正布尔函数及其表达式。

1.2 LMA算法

设堆栈滤波器的输入值为M的非负信号矢量X，X=[X1，X2，…Xn]，Xi∈（0，1，…M-1）。X能够分解成M-1个二进制矢量xm，其中m=0，1，…M -1，为分解维数。可以应用阈值分解函数Tm，可以将Xi分解为

且有

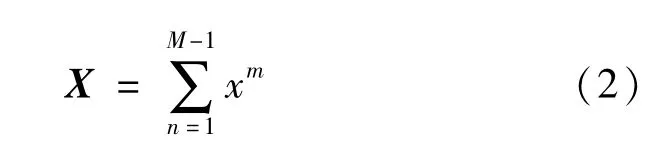
当函数f（·）是具有堆栈性质的正布尔函数时，有

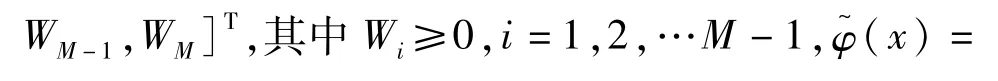
由以上性质可以定义由正布尔函数f（·）定义的堆栈滤波器Sf[5，7]，即:

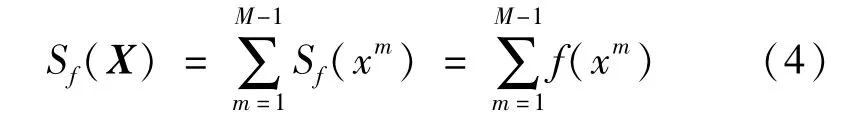
LMA算法的目的就是从所有宽度为N的堆栈滤波器中，挑选一个能够使滤波器输出与理想信号之间平均绝对误差最小的滤波器[8，9]。假设理想信号为S（j），堆栈滤波器的输入为R（j），j表示时域的某一时刻或空域的某一位置，滤波器输出则是对S（j）的估计，用S∧（j）表示，即:

其中，R（n）=[r（n-N1），…，r（n），…，r（n+ N2）]T，N1+N2+1=N，N和N1，N2是整数，则平均绝对误差（MAE）表述为:

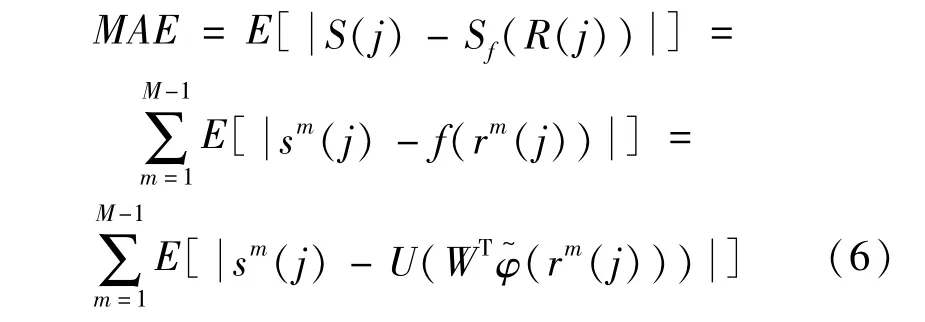
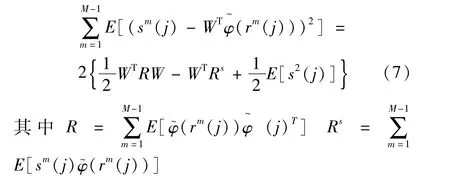
由LMA算法得到的滤波器必须服从堆栈约束，即必须保证滤波器系数Wi≥0，i=1，…，K，K+1。

求最优解W′值的流程应分以下3步:

（1）设置初值将W（0）中所有权值设为正有理数，并为迭代公差Tt赋一个较小的正值。

（2）迭代过程

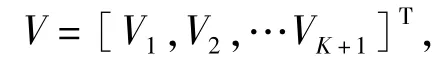
（3）收敛条件 如果

则W（k+1）即为解；否则转向步骤（2），当k→∞时，W（k+1）将收敛于最优解W′。

1.3 递归方案

以上讨论的都是在理想信号S（j）存在的情况下的推导，在实际情况中，由于先验知识的缺失，理想图像通常很难得到。由此，我们将自适应的思想引入到堆栈滤波器中，先将输入信号通过参数可调数字滤波器后产生输出信号，将其与参考信号进行比较，形成误差信号。误差信号通过某种自适应算法对滤波器参数进行调整，最终使误差信号的均方值最小。对于二维图像滤波而言，其中心位置为Yi，j，在噪声图象中选取的相应输入过程R（j）确定后（一般训练样本从整个图像中抽取），我们用直接堆栈滤波合成的图像作为原始期望过程S（j）。由此得到Rs和R后，再利用LMA递推算法得到滤波器的系数W′。用推导出的滤波器对噪声图象进行滤波时，其输出值直接反馈到滤波器的输入端 ，取代所对应的噪声图象信号，并作为滤波器输入信号的一部分。对应着原图像中心位置处Xi，j输出，窗宽度为N×N的滤波窗口[Mi，j]的每个组成单元Yi，j由其对应输出Xi，j之前的输出和其之后的输入决定，由于这些输出值比观测值Xi-N1，…，Xi-1更接近于期望值，因而对于Yi的获得更有帮助。实际过程中，原输出到达Yi，j时，二维窗口开始向右移动一列，按照此向下进行，可得到直接递归得到的图像。由以上过程可知直接递归滤波器模型，如图1所示。

直接递归方案存在的问题是当输入信号中噪声概率较高时，滤波器与输入信号的匹配较差，因此需要进一步优化。从递归的角度讲，由于滤波器的输入已经改变为满足（6）式所表示的形式，推导滤波器的算法采用LMA算法，但对应R和Rs矩阵的估计则采用改变的输入条件，由于滤波后的估计值未知，因此估计R和Rs矩阵时，此时N×N滤波窗口我们称为[M′ij]

图1 直接递归LMA堆栈滤波器模型

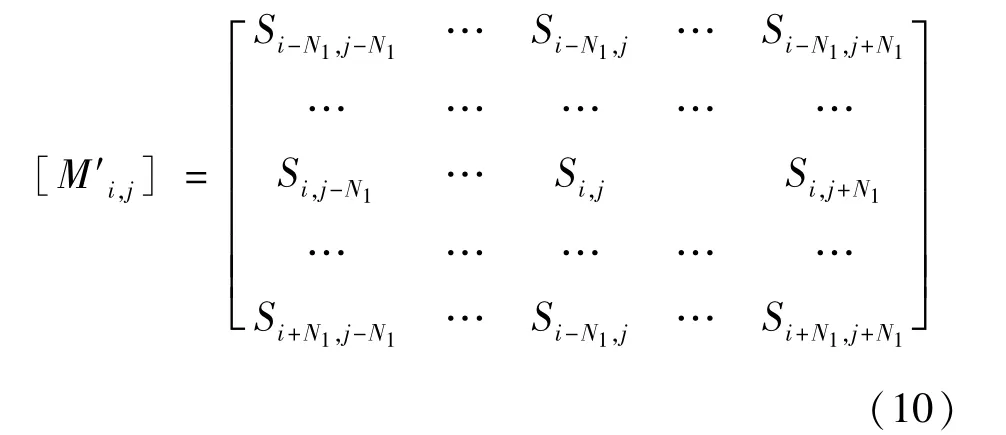
相应滤波器的输出用Si.j替代，更加与滤波器的输入相匹配。因此用所示窗口选取训练样本，来估计R和Rs矩阵，将其代入递推算法后得到的滤波器是与输入样本最佳匹配的滤波器，而且该滤波器的输入窗口仍为原输入窗口，其中通过Hasse图确定堆栈滤波器的正布尔函数[10]，流程图如图2所示。最后的自适应堆栈滤波器流程图如图3所示。

图2 LMA推导下的正布尔函数算法流程

2 基于特征分解的无监督分类方法

地物分类是极化SAR的主要应用之一，分为有监督分类和无监督分类。无监督分类基于特定准则寻找聚类，实现图像分类的自动化处理。现在主流的无监督分类方法主要为基于物理散射特征分类和结合统计特征和物理散射的特征分类。研究采用的是S.R.Cloude和E.pottier提出的H-α/Wishart分类方法[12]。

图3 自适应堆栈滤波器流程图

H-α/Wishart分类方法主要基于相干矩阵（T3）特征值分析的目标极化分散理论。首先用Pauli基矩阵分解可以将后向散射矩阵[S]分解为四个散射机制的相干和，如式（11）所示:

对于定标的后向散射数据，即SHV=SVH，散射机制最一般的表达式可以写成一个复矢量

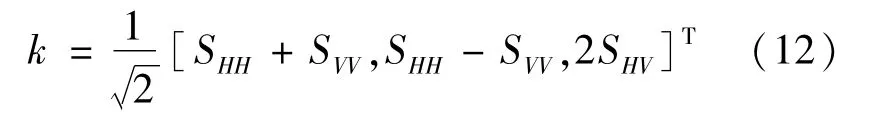
其中，复矢量的第一项的物理意义为单次散射或奇次散射，第二项表示与雷达—目标之间视线成0°的二面角散射，第三项与多次散射有关。

而由于本文的原始数据为斯托克斯矩阵，需要用软件将其转化为相干矩阵后再进行分类操作。而根据相干矩阵特征分解理论，多视处理（n视）的相干矩阵可以写为

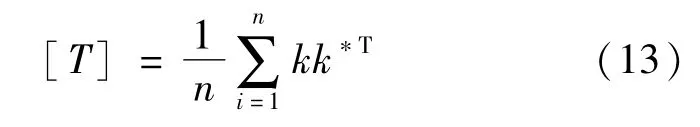
[T]为3×3的半正定Hermitian矩阵。根据特征分解理论，[T]矩阵可以分解为:

λi和ei分别为相对应的特征值和特征向量，且λ1≥λ2≥λ3≥0。特征向量可以写成:

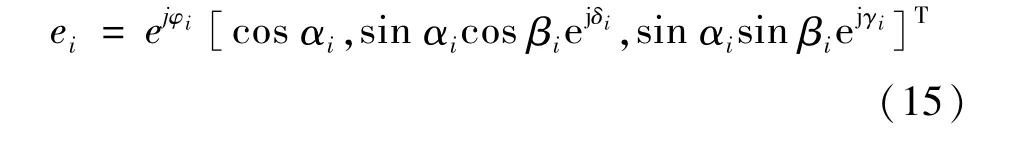
其中，α角对应着从面散射（α=0◦）到偶极子散射（α=45◦）再到导电界面的二次散射（α=90◦）；β角两倍于极化方位角；δ角是SHH+SVV项与SHH-SVV项间的相位差，γ角是SHH+SVV项与SHV项间的相位差；φ角是SHH+SVV项的相位。

Cloude定义了散射熵H（entropy）[8]来表示媒质散射的随机性

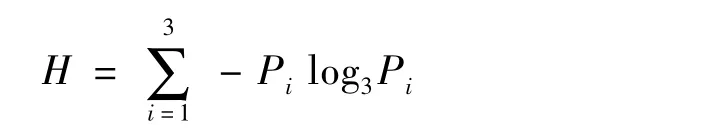
其中

定义了散射角α:

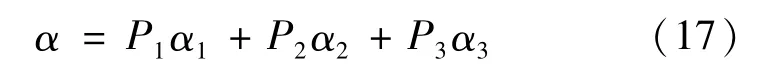
定义了反熵（各向异性）A为

以上定义的三项都属于介质的散射机制，可以用来进行极化数据分类。散射熵H（0≤H≤1）表示散射媒质从各向同性散射（H=0）到完全随机散射（H=1）的随机性，H→0表示各向同性的散射过程，H→1表示完全随机的散射过程。α值与地物散射过程的物理机制相互联系，α→0对应单次散射；α→π/4对应体散射；α→π/2对应二面角散射。反熵A的大小反映了特征分解中第二和第三特征值大小的关系。在实际应用中，只有当H＞0.7时，反熵才作为进一步识别的来源。H和α刻画了介质的散射特征。由H和α组成的特征空间可以划分为八个有效区域，如图4所示。

图4 H-α平面

图4中阴影部分为实际不存在区域，α坐标由下到上分为表面散射（SR），体散射（VD）和二次散射（DR）三部分；H坐标中，（0-0.5）为准确定性区，（0.5-0.9）为中度随机区，（0.9-1）为高度随机区。各个区域代表不同散射特征的物体特征，从而可以作为分类的依据。

在H-α特征参数提出之后，Lee等应用相干矩阵T3或协方差矩阵C服从复Wishart统计分布特征，在H-α分类的基础上利用Wishart分布最大似然分离器改进了上述分类，在8个类别中利用Wishart分布最大似然判定各类间的边界，由于该距离考虑到是整个T矩阵信息，所以其结果具有更好的可靠性[13-15]。

3 实验结果及分析

为了验证研究相干斑滤波和图像分类方法的有效性，选取了NASA JPL AIRSAR荷兰Flevoland地区的P波段极化SAR数据进行实验。像素间距为10 m，数据格式为4视压缩斯托克斯矩阵，场景（750× 1024像素），这里着重考察HH极化数据。

Flevoland地区的极化SAR图像数据的相干斑去噪结果，可知堆栈滤波在去除极化SAR相干斑噪声方面有着明显的效果。如图5所示，由图5的（b）和（d）可知随着递归和自适应方法的引进，自适应堆栈滤波无论是在去噪效果还是保持图像边缘和细节方面相对于直接堆栈滤波都有明显提升。而在与Lee滤波图像的对比中，自适应堆栈滤波在图像边缘保护这一方面有所提升，但是在不同区域边缘周围都有些许的亮噪点，这是由于在跨区域时堆栈滤波造成的。

图5 图像相干斑去噪结果

相干斑滤波后的图像分类效果如图6所示。同相干斑滤波效果很类似的是，通过图（b）和图（d）的比较，可以看出自适应堆栈滤波后对图像分类起到的提升效果。在图像分类效果上，相对于Lee滤波，观察分类后的蓝色低熵区域，整体效果大体一致，反而是Lee滤波的边缘划分更为齐整。由于我们采取的滤窗均匀区域假设，在高随机环境下使得分类仍然可以进行，所以在高熵环境下的二次及多次散射的分类，观察（c）与（d）之间的绿色区域的差异可以看到，图像下方狭窄的绿色区域为连接状态，显然更加符合现实效果。在总体分类效果上，研究也要优于Lee效果。但考虑到Lee方法只需在图像数据处理时即可进行，而研究在实际执行的难易度上还有待改进。

图6 相干斑滤波后H/A/α分类效果

4 结 语

研究将自适应堆栈滤波方法进行改进后应用于极化SAR图像处理，通过LMA算法和递归方案的引进，从降斑噪效果图对比中我们可以得知，递归方法的引进使得图像细节、边缘和对比度上都有了很明显的提升，而从后期的极化SAR图像分类中高熵环境下的局部分类效果对比上也证明了这种方法的有效性。相对于目前主流的滤波手段，自适应堆栈滤波方法有其自身的特点，当然，它在非均匀区域极化信息保持和方法执行难易度上还有待提升。

[1]AKOPIAN D，VAINIO O，AGAIANS，et al.Processors for Generalized Stack Filters[J].IEEE Trans.Signal Processing.1995，SP-43（6）:1541-1546.

[2]LIN YIN，JAAKKO T A.Adaptive Stack Filtering with Application to Image Processing[J].IEEE Trans.Signal Processing，1993，41（1）:162-185.

[3]MARíA ELENA BUEMIetal.Improvement in SAR Image Classification using Adaptive Stack Filters.Brazilian Symposium on Computer Graphics and Image Processing[J]，2007 IEEEDOI10.1109/SIBGRAPI.2007，40:263-270.

[4]JONG-SEN LEE，ERIC POTTIER.极化雷达成像基础与应用[M].北京:电子工业出版社，2013.

[5]J.ASTOLA and P.KUOSMANEN.Fundamentals of Nonlinear Digital Filtering[M].CRC Press，Boca Raton，1997.

[6]J.COYLE AND J.-H.LIN.Stack filters and themean absolute error criterion[J].IEEE Trans.Acoust.，Speech，Signal Processing，1988，36:1244-1254.

[7]CHENK.Bit-serial Realizations of a Class of Nonlinear Filters Based on Positive Boolean Functions[J].IEEE Trans.Circuits And Systems，1989，36（6）:785-794.

[8]张薇，沈永春，张曙.堆栈滤波的递归实现[J].中国图象图形学报，2000，10（5）:851-856

[9]陈贺新.非线性滤波器与数字图象处理[M].北京:国防工业出版社，1997.

[10]王伟，孙圣和，赵春晖.基于Hasse图的层叠滤波器正布尔函数生成算法[J].哈尔滨工业大学学报，2000，1（32）:34-36.

[11]PETER D W et al.Stack Filters.IEEE Transactions On Acoustics，Speech And Signal Processing[J].1986:3-6.

[12]CLOUDE SR，POTTIER E.A Review of Target Decomposition Theorems in Radar Polarimetry[J].IEEE Transaction on Geoscience and Remote Sensing，1996，34（2）: 498-518.

[13]LEE J S，GRUNES M R，KWOK R.Classification of Multi-look Polarimetric SAR Imagery Based on Complex Wishart Distribution[J].International Journal of Remote Sensing，1994，15（11）:2299-2311.

[14]HenriMaître.孙洪译.合成孔径雷达图像处理[M].北京:电子工业出版社，2013.7.

[15]JOHN A.RICHARDS，XIUPING JIA.遥感数字图像分析[M]北京:电子工业出版社，2009.

[16]WIENER N.Nonlinear Problems in Random Theory[M]. New York:The Technology Press，MIT and John Wiley and Sons，Inc.1958

[17]A.LOPES，E.NEZRY，R.TOUZI，AND H.LAUR.Structure Detection and Statistical Adaptive Speckle Filtering in SAR images[J].International Journal of Remote Sensing，1993，14（9）:1735-1758，

[18]D.SMITH.Speckle Reduction and Segmentation of SAR Images[J].International Journal of Remote Sensing，17（11）:2043-205，199.

[19]V.KRISHNAN，Nonlinear Filtering and Smoothing:An Introduction to Martingales[C].Stochastic Integrals and Estimation，New York:Wiley，1984.

白 桦(1981—),男,内蒙古根河市人,硕士,工程师,主要研究方向为雷达工程、微波图像处理；

E-mail：58509350@qq.com

冯恩信(1955—),男,教授,主要研究方向为微波与卫星通信、光纤通信。

Application of Adaptive Stack Filter in Preprocessing of Polarization SAR Image Classification

BAIHua1，2，FENG En-xin1
（1.Xi'an Jiaotong University，School of Electonics and Information Engineering，Xi'an，Shan Xi710049，China；2.PLA 63898 troops，Ji Yuan，He Nan 454001，China）

As a special case of non-linear filters，stack filters have a good performance for filtering imageswith different types of noisewhile preserving edges and details.In this paper，a adaptive stack filter is designed for the preprocessing of classification of polarimetric Synthetic Aperture Radar（pol-SAR）images，which are affected by speckle noise.The recursive implementation approach of optimal stack filters under MAE criterion is advanced in shorting the running time of the filtering procedure and improve the quality of the output.The results from the output of stack filter are extracted into polarized characteristics firstly by using the H/A/αdecomposition method.And based on these characteristics，applying H-α/ Wishart methodswill help us to classify the information in the SAR image.The effects of classification are evaluated and then are compared with the results of classifying the imageswith othermethods of filtering.

Stack filter；Image Classification；pol-SAR；H-α/Wishart classify

TN957.52

A

1673-5692（2015）02-213-06

10.3969/j.issn.1673-5692.2015.02.019

2015-03-09

2015-04-03