基于相参雷达信号自相关函数的分选方法

韩 俊,何明浩,郭利荣,魏晴昀

(空军预警学院,湖北武汉 430019)

工程与应用

基于相参雷达信号自相关函数的分选方法

韩 俊,何明浩,郭利荣,魏晴昀

(空军预警学院,湖北武汉 430019)

为解决信号分选中的“漏批”问题,提出了一种基于相参雷达信号自相关函数的分选新方法。该方法利用相参信号的瞬时自相关函数,建立了峰值比判决模型,并对该模型进行分选仿真应用。仿真结果表明,在信噪比高于5 dB时,方法能够解决单频、线性调频、非线性调频脉冲串信号一次分选过程中的“漏批”问题,验证了所提出方法的有效性。

相参；自相关函数；峰值比；信号分选

0 引 言

雷达辐射源信号分选，特别是复杂电磁环境下未知参数的雷达辐射源信号分选是电子情报侦察系统（ELINT）和电子支援系统（ESM）中的重要组成部分，只有在分选的基础上，才能对雷达辐射源信号的参数进行分析和提取，对雷达类型和威胁性质进行识别。

传统的辐射源信号分选识别方法主要基于五维参数，其中，PRI分选是应用较为普遍的一种分选方式[1-3]。随着电子技术的发展，雷达的工作体制越来越复杂，在信号分选过程中，经过一次信号分选后，各个辐射源脉冲信号的许多参数仍然表现出多极化，这主要信号没有被分选彻底的原因。特别是不同辐射源发出的同频信号，经常由于缺乏有效的特征判定参数，而被误判为同一辐射源信号，造成“漏批”问题。近年来，针对雷达辐射源信号新特征参数的提取，许多学者又提出模糊函数[4]、原子分解[5]、经验模态分解[6]、相位差分[7]等多种方法，甚至有增加分选特征参数的方法[8]。利用这些方法在一定程度上可以提高信号分选的准确率，但是，基于现有分选参数的分选方法都无法有效解决“漏批”问题。

研究基于相参雷达信号自相关函数，提出了一种新的信号分选方法。利用瞬时自相关算法，对一次信号分选的结果进行二次分选。通过判断自相关函数的差异，判定一次分选后的各个辐射源脉冲串是相参信号还是非相参信号，进而可以确定在一次分选中是否存在“漏批”问题，对一次信号分选提供补充。

1 瞬时自相关函数定义

相关函数是描述随机样本函数在不同时刻瞬时值之间的关联程度，可以简单描述为振动波形随时间坐标移动时与别的波形的相似程度[9]。信号的瞬时自相关函数，是指当前信号与经过一定时延信号之间的相关函数，它反映了前后信号之间的相关程度。相参性作为脉冲信号的一种脉间信息，表示的是前后脉冲之间相位信息的相关性与连续性。因此，可以利用瞬时自相关函数判别前后脉冲之间的相参特性。

设侦察接收信号形式为s（t），则自相关函数定义为[10]

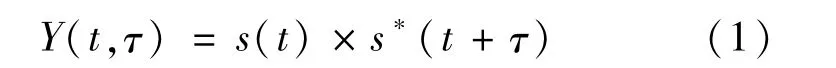
Y（t，τ）与一般自相关函数的最大区别就是它没有时间积分，所以保留了相关处理的瞬时信息，对应的数字表示是Y（n，m）

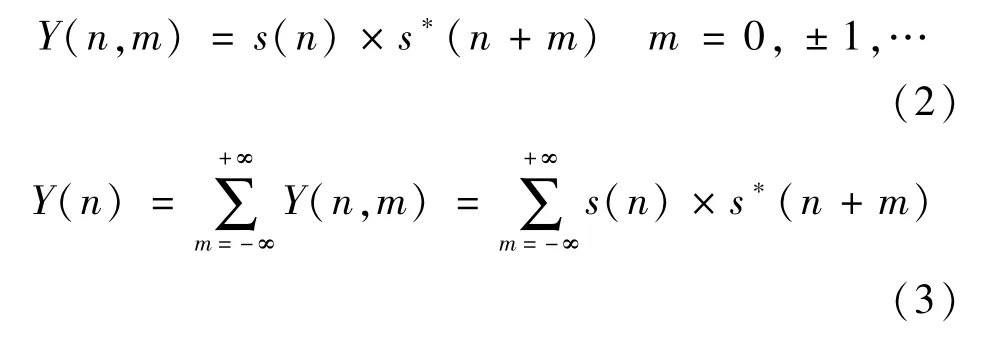
2 信号瞬时自相关函数仿真

根据侦察接收得到的结果以及一次分选的数据，如载频、脉冲重复间隔、脉宽等，对一次分选后的信号进行自相关函数运算。

取两组脉冲串信号，其中一组为相参脉冲串信号，另一组为非相参脉冲串信号，信号的中频都为30 MHz，脉冲重复周期PRI=30μs，脉宽τ=10μs，发射相参脉冲串的雷达辐射源信号初始相位相同，发射非相参脉冲串的雷达辐射源初始相位不同。每串脉冲的个数为10，采样频率100 MHz，分别对两组信号按照公式（3）作自相关运算，仿真结果如图1、图2所示。

从图1和图2中可知，在零点附近，相参脉冲串信号与非相参脉冲串信号的相关性大致相同，在零点以外，相参信号的相关性比非相参信号的相参性好得多。相参脉冲串信号的相关性随着延迟时间的增大呈现稳步的周期性下降趋势，而非相参脉冲串信号的相关性从零点到下一个峰值点差距明显。表明:与相参脉冲串信号相比，非相参脉冲串信号相关性较差。在多次实验中，相参脉冲串信号的自相关函数，不管运算多少次，其结果都是完全一致的；非相参脉冲串信号的自相关函数运算结果有明显的随机波动性。

图1 相参脉冲串信号自相关函数

图2 非相参脉冲串信号自相关函数

为研究脉内调制信号的相关性，分别取两组线性调频脉冲串信号，其中一组为相参信号，另一组为非相参信号。信号中频都为30 MHz，带宽10 MHz，采样频率100 MHz，脉冲重复周期PRI=30μs，脉宽τ=8μs，发射相参脉冲串的雷达辐射源信号初始相位相同，发射非相参脉冲串的雷达辐射源初始相位不同。将两组脉冲串信号分别作相关函数运算，仿真结果如图3、图4所示。

从图3和图4中可知，线性调频脉冲串信号的相关性与单频点脉冲信号的相关性具有类似性；相参线性调频信号较非相参线性调频信号具有更好的相关特性。

图3 相参线性调频脉冲串自相关函数

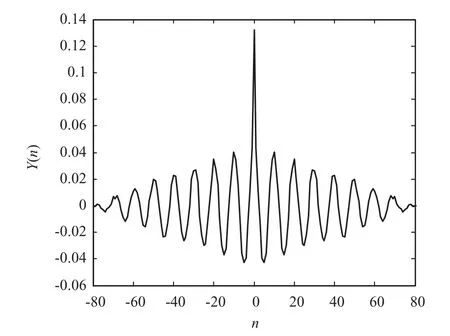
图4 非相参线性调频脉冲串自相关函数

图5 相参非线性调频脉冲串自相关函数

图6 非相参非线性调频脉冲串自相关函数

同理，取两组非线性调频信号，一组为相参脉冲串，另一组为非相参脉冲串信号。信号中频为200 MHz，带宽10 MHz，脉冲重复周期PRI=30μs，脉宽τ=15μs，发射相参脉冲串的雷达辐射源信号初始相位相同，发射非相参脉冲串的雷达辐射源初始相位不同。将两组脉冲串信号分别作相关运算，仿真结果如图5、图6所示。

从图5和图6中可知，非线性调频信号的自相关函数在变化规律上与单频、线性调频等样式的信号相似。

综合以上的仿真分析，相参信号的自相关性要好于非相参脉冲信号的自相关性，提取这一特性可以作为信号的相参特征参数，并将其应用于雷达信号分选中。

3 峰值比判决模型分析与仿真

由第2节分析可以得出，相参脉冲串信号与非相参脉冲串信号自相关函数最大的区别就是相关函数峰值点的变化规律不同。设原点为第一峰值点，紧靠原点右侧的峰值点为第二峰值点，依此类推。那么，对于相同调制样式的信号，相参脉冲串第二峰值点的值比非相参脉冲串第二峰值点的值要高出两倍左右。利用这一特征提出了峰值比判决模型。

3.1 峰值比判决模型

除第一峰值点外最大的峰值点与第一峰值点的比值定义为峰值比L

其中，R（1）为原点处对应的相关函数第一峰值点。

利用峰值比模型进行运算，按照第2节中仿真条件，得到各种类型相参与非相参脉冲串信号的峰值比结果如表1所示。

表1 相参与非相参脉冲串信号峰值比结果

由计算结果得到，相参脉冲串信号的峰值比接近1；非相参脉冲串信号的峰值比较小。利用这一参数的差异，可以将相参脉冲串信号与非相参脉冲串信号进行区分。

做100次蒙特卡罗实验，运算中随机选取单载频、线性调频、非线性调频等样式的信号，脉冲信号占空比为0.05~0.4，信噪比为（5~15）dB之间的整数值，各次运算的峰值比结果如图7所示，其中虚线部分为非相参脉冲串信号的峰值比仿真结果。由仿真结果得到:相参脉冲串信号的峰值比基本都大于0.5，而非相参脉冲串信号的峰值比都小于0.5，因此，可以定义0.5为判决门限，当峰值比大于0.5时，判定为相参信号；当峰值比小于0.5时，判定为非相参信号。

图7 100次运算得到的峰值比结果分布曲线

3.2 信噪比误差

为验证判决门限的准确性和适用范围，现考虑噪声因素的影响。选择中频为30 MHz，采样率100 MHz，脉宽10μs，脉冲重复间隔50μs，取10个脉冲，分别计算信噪比在5 dB、10 dB和15 dB的情况下，相参与非相参脉冲串信号峰值比结果如表2所示。

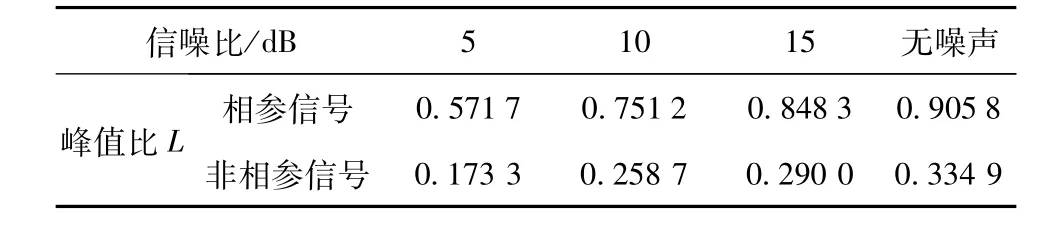
表2 不同信噪比下峰值比仿真结果

由仿真结果得到，当有噪声存在时，峰值比结果会受到影响，但是，在信噪比大于5 dB时，相参脉冲串峰值比总是大于0.5，非相参脉冲串信号峰值比总是小于0.5。也就是说，噪声虽然对瞬时相关结果有影响，但是并不影响以0.5为门限的判决结果。峰值比判决方法能够适用于信噪比高于5 dB的情况，这在真实信号环境中是能够满足的。

4 分选判决模型应用

分别取10组脉冲串信号，信噪比取10 dB，其中，前5组信号为相参脉冲串信号，信号中频30 MHz，脉冲重复间隔50μs，占空比分别为1/3、1/4、1/5、1/8、1/10，调制样式分别为:固定频率、线性调频（带宽10 MHz）、非线性调频（带宽10 MHz）、线性调频（带宽 15 MHz）、非线性调频（带宽15 MHz）；后5组信号为非相参脉冲串信号，仿真条件与前面5组信号相同。利用基于自相关函数的峰值比判决模型进行分选，结果如表3所示。

表3 相参与非相参信号相关运算后各个峰值点数值

由分选结果可看出，脉冲串1、2、3、4、5峰值比大于0.5，根据判决准则，判定为相参信号；脉冲串6、7、8、9、10峰值比小于0.5，判定为非相参信号，与实验假设相符，验证了分选判决模型的有效性。

进行100组上述实验，在不同信噪比条件下可得到信号分选“漏批”概率与信噪比的关系如图8所示。

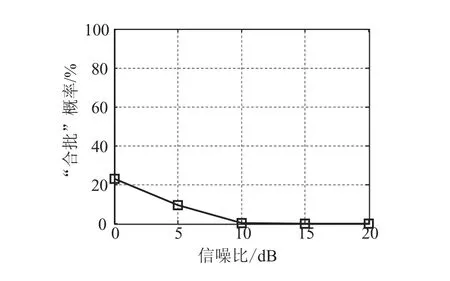
图8 不同信噪比下信号分选的“漏批”概率

从图8中可得出，利用基于峰值比的分选方法对脉冲信号进行分选后，分选的“漏批”现象得到很大程度的改善，当信噪比为5dB时，分选的“漏批”概率下降为10%，当信噪比为8dB时，分选的“漏批”概率仅为5%，当信噪比大于等于10dB时，分选的“漏批”概率趋于0。可见，基于峰值比的分选方法，可以有效降低信号分选的“漏批”概率。

在实际信号分选中，调制频率相同的信号在脉冲重复间隔等调制参数差距不明显的情况下，经常会被误判为同一辐射源发出的信号，出现“漏批”问题，影响到信号后期的识别与判型等。利用自相关函数的峰值比判别方法，就是对传统信号分选结果进行二次分选验证，可以减少“漏批”问题，提高分选方法的分选准确率。基于自相关函数的改进信号分选流程图，如图9所示，其中虚线框中部分为提出的“漏批”分选方法。

图9 基于自相关性的改进信号分选流程图

5 结 语

研究基于相参信号的自相关性，提出了一种新的信号分选方法。首先介绍了自相关函数的定义，并对相参与非相参信号的自相关函数进行仿真分析，在这基础上提出了峰值比判决模型，并对该模型进行分选仿真应用，用于信号二次分选，最后设计了基于自相关性的信号分选方法。仿真结果表明，所提出的方法能够解决单频、线性调频、非线性调频脉冲串信号一次分选过程中的“漏批”问题。

[1]张什永，胡泽宾，王俊文.基于变换谱相干积累的片段信号PRI检测[J].雷达科学与技术，2012，10（3）:286-289.

[2]王海滨，马琦.一种基于PRI变换的雷达信号分选方法[J].现代电子技术，2013，36（1）:28-31.

[3]NISHGUCHI K.，KOBAYASHIM.Improved Algorithm for Estimating Pulse Repetition Intervals[J].IEEE Trans on AES，2000，36（2）:407-421.

[4]普运伟，金炜东，朱明等.雷达辐射源信号模糊函数主脊切面特征提取方法[J].红外与毫米波学报，2008，27（2）:133-137.

[5]朱明，金炜东，胡来招等.基于原子分解的雷达辐射源信号二次特征提取[J].西南交通大学学报，2007，42（6）:659-664.

[6]HU HONG-YING，KANG JING，GUAN LI-NA.Instantaneous Frequency Estimation Based on Empirical Mode Decomposition[C].Proceedings of the 7th Wor1d Congress on Intelligent Control and Automation，Chongqing，China，June 25-27，2008.

[7]韩俊，何明浩，朱元清，等.基于多参数的雷达辐射源分选新方法[J].数据采集与处理，2009，24（1）: 91-94.

[8]孟祥豪，罗景青.基于合成特征参数和脉冲样本图的雷达信号分选[J].火力与指挥控制，2012，37（9）: 50-54.

[9]李要军，李萍，褚福磊.基于相关函数的多振动信号数据融合方法[J].震动、测试与诊断，2009，29（2）: 179-183.

[10]赵国庆.雷达对抗原理[M].西安:西安电子科技大学出版社，1999.

Sorting M ethod Based on Coherent Radar Signal Auto-correlation Function

HAN Jun，HE Ming-hao，GUO Li-rong，WEIQing-yun
（Air Force Early Warning Academy，Wuhan 430019）

To solve the Increasing-batch problem in signal sorting，a new sorting method based on autocorrelation function of coherent radar signal is proposed in this paper.By using the instantaneous autocorrelation function of coherent signal，the discrimination model of ratio of peak valueswas built and applied in sorting simulation.Simulation results show that the proposed approach can solve the Increasingbatch problem for CW、LFM、NLFM one sorting when the signal-to-noise rate（SNR）above 5dB.The validity of the approach is demonstrated by experimental results.

Coherency；auto-correlation function；ratio of peak values；signal sorting

TN971

A

1673-5692（2015）02-204-05

韩 俊(1983—),男,安徽合肥人,博士,工程师,主要研究方向为雷达信号处理、电子对抗信息处理等；

E-mail：duj81@163.com

何明浩(1963—),男,江苏江阴人,博士,教授,博士生导师,主要研究方向为雷达系统,雷达与对抗等；

郭利荣(1988—),男,福建建瓯人,硕士研究生,主要研究方向为电子对抗信息处理；

魏晴昀(1974—),女,湖北武汉人,硕士,副教授,主要研究方向为电子对抗技术。

10.3969/j.issn.1673-5692.2015.02.017

2014-12-03

2014-12-29