频率调制信号调制方式识别方法

武者东,侯国涛,孙中森,柳 颖

(中国电波传播研究所,山东青岛 266107)

工程与应用

频率调制信号调制方式识别方法

武者东,侯国涛,孙中森,柳 颖

(中国电波传播研究所,山东青岛 266107)

为完成对FM,2FSK,4FSK,8FSK,MSK等频率调制信号的识别,在瞬时频率直方图统计图、信号功率谱、信号平方谱等提取特征,这些特征提取简单,计算量小.给出了频率调制信号识别算法,并利用实测数据验证算法的性能及算法对脉冲成形滤波器形状,频偏等因素的鲁棒性。

频率调制信号,调制方式识别,瞬时频率直方图,谱特征

0 引 言

通信信号的调制方式自动识别是盲信号接收和解调的关键环节，对信号自适应接收和智能通信等具有重要意义，可以应用在电子对抗、频谱监测、干扰识别、认知无线电等多种军用和民用场合。

目前的调制识别算法可以分为判决理论识别方法和统计模式识别方法。由于需要一些先验知识，使得判决论方法应用受到很大限制。统计模式识别方法不需要接收信号的先验知识，从而受到广泛关注和应用。

统计模式识别方法主要工作为分类特征提取和分类器的设计，其中分类特征是区别统计模式识别方法的主要因素。由于频率调制信号具有技术成熟、成本低廉等优点，不论在军用、民用领域占有重要的地位，所以对频率调制类信号调制方式识别的研究有着重要的意义。研究主要分析了频率调制信号的调制方式识别方法。以往的研究有的采用瞬时特征参数统计方法[1-2]，有的采用高阶统计量方法[3-4]，有的采用功率谱特征方法[5]，和其他方法[6-7]。这些方法要么没有考虑脉冲成型滤波器影响，要么对频偏比较敏感，要么计算量大不适合实时处理。研究在总结以往经验的基础上，在瞬时频率直方图统计图、功率谱及平均谱等特征上归纳总结，提出了健壮的频率调制识别方法。

1 信号模型及特征分析

1.1 信号模型

研究选取FM，2FSK，4FSK，8FSK，MSK等5种信号作为研究对象。

信号经过模拟接收机下变频为固定中频，然后利用带通采样定理经数字信号采集板对其采集，接收的信号建模如下。

FM信号:

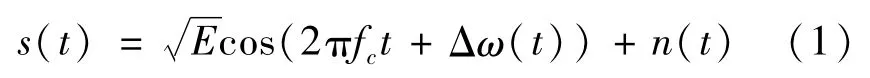
MFSK信号:

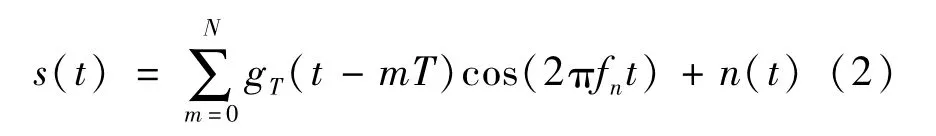
式中，N为观测码元数目，T为码元宽度；gT（t）为脉冲成形滤波器，fn∈{f1，f1，…，fM}，一般情况下，Δf=f2-f1=…fM-fM-1，Δf称为频率间隔。MSK为2FSK的一种特例，其调制指数h=0.5。

1.2 特征分析

文献[2]中提出利用零中心归一化瞬时频率的紧致性（四阶矩）来区分FM和MFSK。此参数不能将FM与MSK分开，且在低信噪比时区分FM与MFSK能力有所下降，故此参数不具备健壮性。

FM与MFSK本质区别为FM的瞬时频率是以一个载频为中心频率随调制信号连续变化的，而MFSK有2个以上的载频。通过瞬时频率直方图统计信息对FM与MFSK进行分类。

1.2.1 瞬时频率直方图平坦度

文献[5]中区分FM与MFSK类信号用到信号功率谱的平坦度指数，由于平坦度指数计算首先需要估计信号带宽等参数从而降低了该参数的应用范围。研究将分析采用瞬时频率直方图统计中的平坦度，并利用其对MFSK与FM进行分类。

设被评估曲线长度为N，评估窗口宽度为M，平坦度指数描述曲线的起伏状态，定义为:

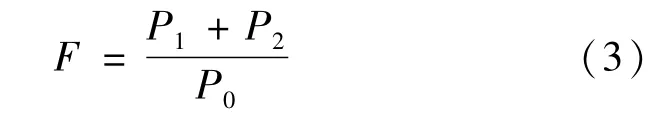
P0为曲线中心评估窗口内最大值，即:

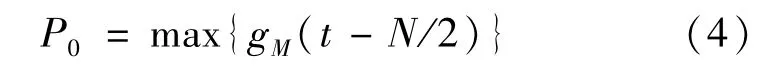
式中gM（·）为宽度为M的窗函数。

P1，P2为距离曲线中心δN点（δ为小于1的数，具体数值根据曲线形状确定）评估窗口内最大值，即:

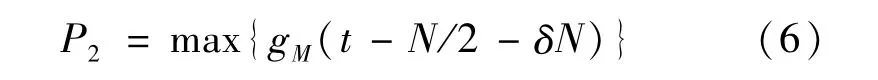
如果曲线平坦，F≈2；如果曲线是单峰形状，F＜2；如果曲线是多峰形状，F＞2。因而该参数可以把单峰曲线与多峰曲线区分开，符合FM与MFSK本质区别特征。

设信号采样速率为fs，码元速率为Rb，则每个码元采样点数为R=fs/Rb，则观察码元数目N内共有采样点数N×R。瞬时频率直方图提取流程如下:

（1）以M点为帧长度，将总采样点数N×R分为N×R/M帧；

（2）每帧内计算截获信号的瞬时频率，瞬时频率的计算参考文献[1][8]等；

（3）对瞬时频率去直流分量，校正频偏的影响，并对fs/2进行归一化；

（4）对每帧的瞬时频率进行直方图统计；

（5）重复（2）~（4）计算所有帧的瞬时频率直方图统计信息；

（5）对所有帧的瞬时频率直方图取均值。瞬时频率直方图提取流程如图1所示。

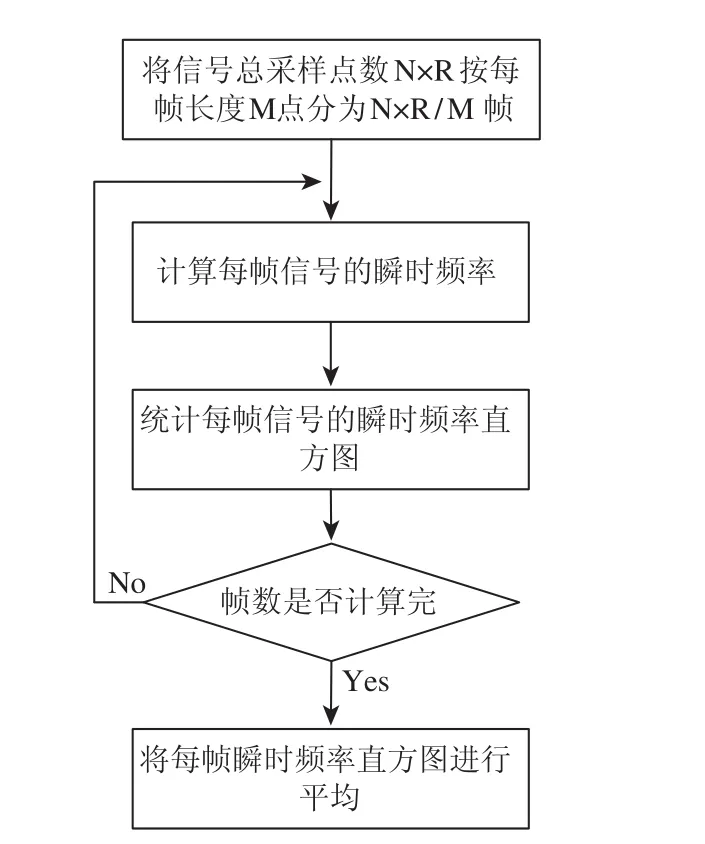
图1 信号瞬时频率直方图提取流程图

FM，MFSK，MSK等频率调制信号的瞬时频率直方图仿真图如图2~图7所示。

由图2可知，FM瞬时频率直方图统计图具有单峰波形特点。图中FM信号采用山东省青岛市城阳区人民广播电台，频率94MHz。

图3~图7中的信号是由安捷伦E4438C信号源产生，模拟接收机接收信号后下变频为固定中频，经采集设备采样后获得零中频数字IQ信号。由图3、图4可知，4FSK瞬时频率直方图统计图具有多峰波形特点，且对脉冲成形滤波器的滚降因子不敏感。图3、图4中脉冲成形滤波器类型采用Nyquist，滚降因子α取值为0.1、0.9。当4FSK信号脉冲成形滤波器类型采用RootNyquist时，滚降因子α取值从0.1~0.9，结果与Nyquist一致。2FSK的瞬时频率直方图统计图也为多峰，平坦度参数对脉冲成形滤波器及滚降系数不敏感。

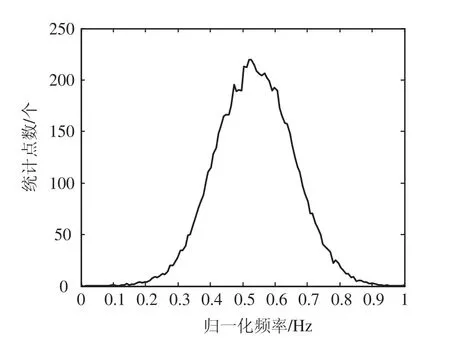
图2 FM瞬时频率直方图统计图

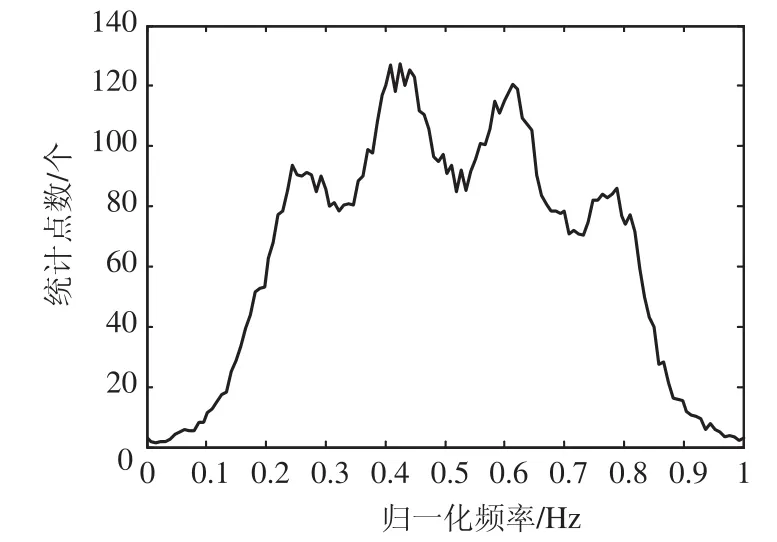
图3 4FSK瞬时频率直方图统计图

图4 4FSK瞬时频率直方图统计图

由图5可知，当调制信号为8FSK，即使调制指数较大为h=1.0时，其瞬时频率直方图统计图没有呈现多峰，主要由于脉冲成形滤波器引起。在加大码元数目情况下，瞬时频率直方图统计图仍没有出现明显的多峰。

由图6可知MSK信号瞬时频率直方图统计图同样呈现多峰，且不受脉冲成形滤波器和滚降因子影响。

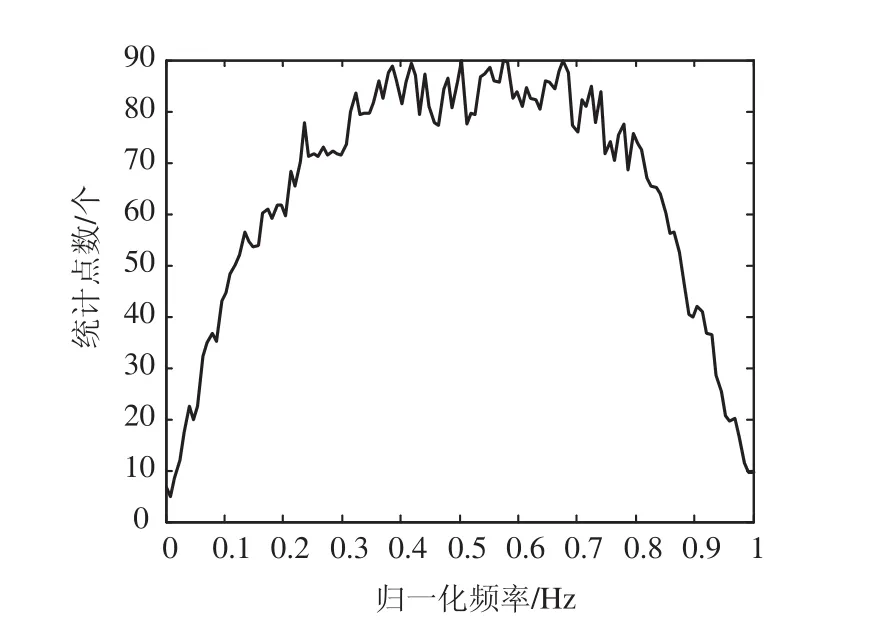
图5 8FSK瞬时频率直方图统计图

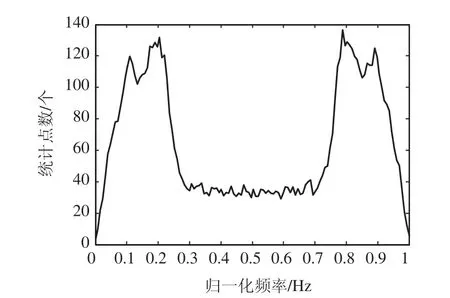
图6 MSK瞬时频率直方图统计图

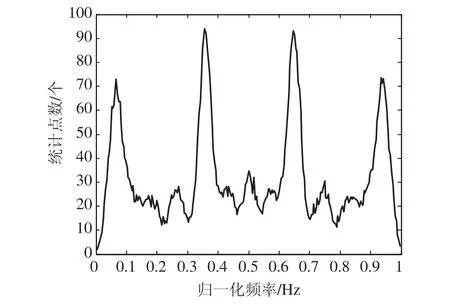
图7 频偏对4FSK瞬时频率直方图统计图影响图

由图7可知，FrequencyOffset=（0.5Rb）Hz时，由于瞬时频率计算采取了去直流措施，瞬时频率直方图统计图不受频偏影响。仿真表明FrequencyOffset=（0.1Rb）Hz~（0.5Rb）Hz步进为0.1Rb，瞬时频率直方图统计图均不受影响。

从仿真可知，通过瞬时频率直方图统计图的平坦度系数可以将{FM}与{MFSK，MSK}很好的区分。但8FSK脉冲成形滤波器类型采用Nyquist，RootNyquist时瞬时频率直方图统计图没有呈现多峰，因此研究只考虑矩形脉冲成形滤波器的8FSK信号。

1.2.2 瞬时频率直方图峰数

MFSK类信号用矩形脉冲成形滤波器时，瞬时频率直方图峰数可以很好的区分MFSK的调制阶数M。

8FSK信号采用矩形脉冲成形滤波器时，直方图仿真图如图8所示。低调制阶数矩形脉冲成形滤波器的MFSK瞬时频率直方图统计图均出现了与其阶数相匹配的峰数。

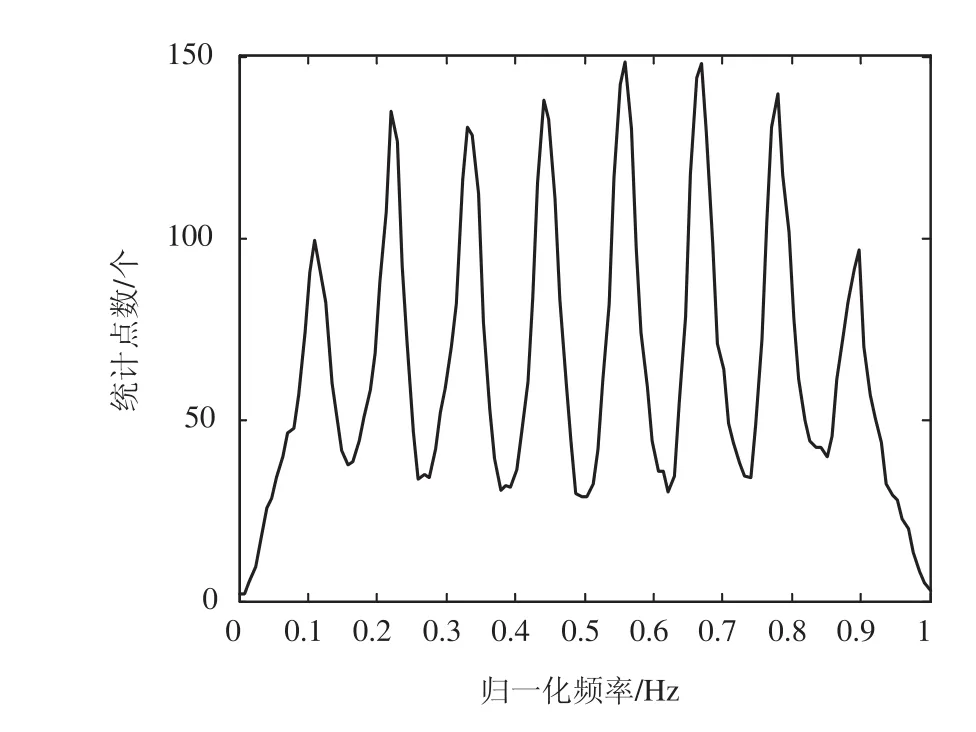
图8 8FSK瞬时频率直方图统计图

1.2.3 功率谱、平方谱特征

信号功率谱谱峰数N1，信号平方谱谱峰数N2定义见参考文献[5]。众所周之，MFSK信号在调制指数h=1.0，2.0时，功率谱出现与阶数相同的单频分量，MSK平方谱出现单频分量。

2 识别算法

识别算法流程为，首先计算待识别频率调制信号的各特征参数，然后将计算出的特征参数按照图9所示流程完成调制模式识别。

图9中各参数说明如下:

N1:信号功率谱谱峰数；N2:信号平方谱谱峰数；Ff:瞬时频率直方图平坦度指数；Nf:瞬时频率直方图峰数；Th1~Th8为识别支路对应的门限。

3 算法仿真与分析

对FM，2FSK，4FSK，8FSK，MSK等信号的调制识别算法性能在matlab平台上进行了仿真。FM信号来源为青岛市各广播电台信号，其余信号由安捷伦信号源E4438C产生。2FSK，4FSK信号调制指数从0。1到1，步进为0.1，调制指数1.1，1.4，1.5， 1.9，2；脉冲成形滤波器类型选择矩形，RootNyquist，Nyquist类型等，RootNyquist，Nyquist类型时滚降系数α从0.1到0.9，步进为0.1。8FSK调制指数从0.1到1，步进为0.1，1.5，1.6，1.9，2。MSK脉冲成形滤波器类型选择RootNyquist，Nyquist类型，滚降系数α从0.1到0.9，步进为0.1。在matlab平台下对采集的信号添加了噪声，噪声带宽为fs/2Hz。研究对调制识别算法进行了大量的仿真，当信噪比为0 dB时，仿真结果如表1所示。

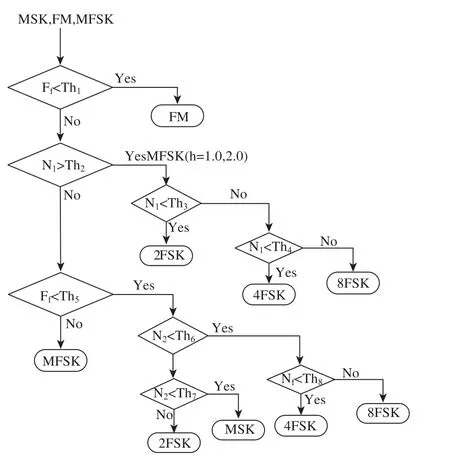
图9 频率调制类信号调制识别流程图

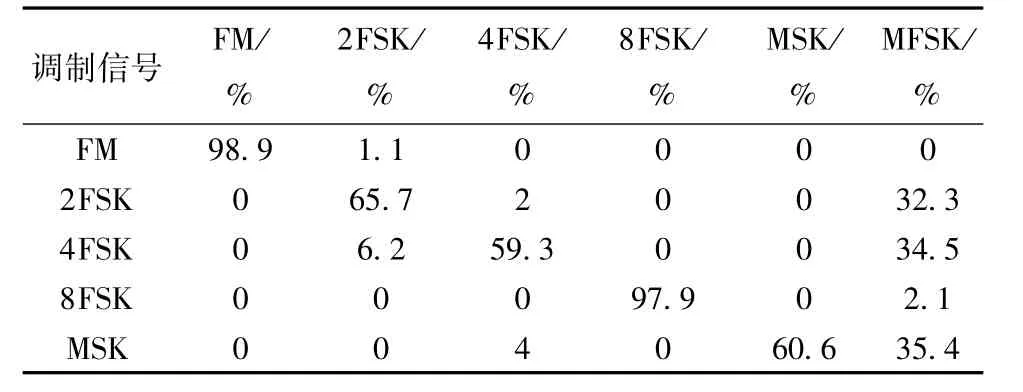
表1 SNR=0 dB时各信号调制识别率

由表1可知，2FSK，4FSK，MSK部分信号被识别为MFSK信号，由于2FSK、4FSK调制指数较小且采用RootNyquist、Nyquist类型脉冲成形滤波器的滚降系数较小时，瞬时频率直方图统计图虽然呈多峰形状，但给机器识别图中的峰数带来了很大困难，如图3、图6所示。这是识别低调制指数非矩形脉冲成形滤波器的MFSK阶数M下一步的工作。

4 结 语

研究分析了频率调制信号的瞬时频率直方图、功率谱、平方谱等特性，然后提出了分类特征参数，并设计了调制识别的流程。仿真表明，分类特征参数对脉冲成形滤波器类型，频偏等不敏感，调制识别算法在较低的信噪比下识别率很高。下一步将解决调制指数小且非矩形脉冲成形滤波器滚降系数小时调制阶数M的识别。研究提出的识别算法可以识别常用的频率调制信号，并且实现简单、识别性能好，具有很好的实用性。

[1]AZZOUS E.E.，NANDI A.K.Automatic Modulation Recognition of Communication Signals[M].Netherlands: Kluwer Academic Publishers，1996.

[2]付仕平，杨丽，邵伟.基于瞬时特征参数的数字信号调制识别算法[J].现代防御技术，2013，41（6）:71-75.

[3]周敏，冯全源.数字调制信号制式识别新方法[J].电讯技术，2012，52（4）:519-522.

[4]宋娇，葛临东.一种基于高阶累积量的FSK信号识别新方法[J].通信技术，2008，41（04）:4-6.

[5]范海波，杨志俊，曹志刚.卫星通信常用调制方式的自动识别[J].通信学报，2004，25（1）:140-149.

[6]王蒙，于宏毅，胡赟鹏，等.基于特征选择和支持向量机的数字调制识别方法[J].信息工程大学学报，2013，14（4）:410-414.

[7]姚亚峰，陈建文，黄载禄.频率调制信号的恒参滤波识别方法[J].华中科技大学学报（自然科学版），2004，32（7）:48-50.

[8]黄知涛，周一宇，姜文利.基于相对无模糊相位重构的自动脉内调制特性分析[J].通信学报，2003，24（4）: 153-160.

武者东 (1982—),男,山东人,工程师,主要研究方向为无线电监测,信号处理等；

E-mail：332595526@163.com

侯国涛(1982—),男,河北人,工程师,主要研究方向为无线电监测,通信信号盲处理,雷达对抗等；

孙中森(1980—),男,山东人,高级工程师,主要研究方向为无线电监测,信号处理等；

柳 颖(1981—),女,山东人,讲师,主要研究方向为信号与信息处理。

The Recognition M ethod of Frequency M odulated Signal

WU Zhe-dong，HOU Guo-tao，SUN Zhong-sen，LIU Ying
（China Research Institute of Radiowave Propagation，Shandong Qingdao 266107，China；）

To classify the type of signal such as FM，2FSK，4FSK，8FSK，and MSK，a novel recognition scheme based on the feature of instantaneous frequency histogram，signal power spectrum and the power spectrum of the second power of signal is proposed.These feature parameters have the characters of easy extraction and small amount of calculations.It is illustrated by the test results for the performance of the algorithm using the actual data.Simulation results show that the algorithm is not sensitive to the type of pulse shaping filter or frequency offset.

Frequency modulated signal；modulation recognition；instantaneous frequency histogram；spectrum feature

TN934

A

1673-5692（2015）02-199-05

10.3969/j.issn.1673-5692.2015.02.016

2015-01-30

2015-03-24