射表误差及对射击精度的影响分析

朱训慧，赵健康，闫 浩

（装甲兵学院，安徽 蚌埠 233050）

射表误差及对射击精度的影响分析

朱训慧，赵健康，闫 浩

（装甲兵学院，安徽 蚌埠 233050）

以车载武器为研究对象，明确了射表的作用和基本要求，分析了射表误差的组成因素和简要计算方法，在此基础上剖析了射表误差对射击精度的影响。提出了射表误差是目前条件下影响车载武器射击精度主要因素的观点，可对研究车载武器射击精度提供一定参考。

车载武器，射表误差，射击精度

0 引言

射表是记载某种武器射击时的弹道诸元、修正诸元、散布诸元和有关使用武器、弹药规定的文件（表册）。是正确使用武器，充分发挥武器性能，进行精确射击和研究射击理论的重要依据。比如，在武器制造方面，表尺分划的刻制、火控计算机解算程序的编制都离不开射表；在武器使用方面，非表定条件下射击诸元的确定、射击误差的修正，没有射表也无法进行；在理论研究方面，要评判射击效率，确定武器的有效射程、直射距离、命中界，分析武器的射击精度等，也都需要射表。

1 对射表的基本要求

要想使武器发射的弹丸准确地命中目标，其射表首先必须具有足够的精度。对射表精度要求的标准，不是一成不变的，而是随着武器射击条件的变化而变化的。武器射击准确度的好坏，是由射击准备误差决定的，这其中就包含了射表的误差。

假设：某种火炮的射击准备误差有两个方面组成，一方面是除射表误差以外的其他误差E1，另一方面是射表误差E2，则射击准备的综合中数误差Ez：

由于射表误差增大而使射击准备误差增加的情况，可用下列的比值Ez/E1的百分数来表示。

由表1可以看出，首先对射表精度的要求，随着武器射击准备误差的减小而提高。如果抛开武器射击准备的精度而片面追求射表精度的提高，不仅对射击准确度不会产生提高的效果，反而会造成编制射表方面对人力、物力时间的浪费。相反，如果抛开射表的精度，片面地追求减小射击准备的其他误差，在一定的条件下对射击准备精度的提高也是无济于事的。

其次，要求射表在内容上还须具有一定的完整性。也就是说射表必须具备保证武器准确射击的所有诸元。如弹道诸元、修正诸元、散布诸元以及为了修正和射击计算所必须的若干附表和说明等。但事物总是一分为二的，如果射表过于完整，势必篇幅过大，携带查用不方便。为此，一方面对完整射表所选距离间隔不宜过小（一般为100 m～200 m），这样既可使篇幅缩小，又能使在间隔内的距离可用简单的直线插值求得；另一方面，对于近距离射击的武器，可根据实战情况不同而编制简化程度不同的简要射表。

最后，射表还须具备在战斗条件下的耐用性和方便性。即需考虑其体积大小，便于袋装携带；字体大小，清晰易认；内容简明，查取迅速；坚韧耐磨，防潮抗污。至于简要射表要简单到什么程度，应根据武器可能使用的具体条件来确定。完整射表的过于完整或简要射表的过于简单，均非所宜。

2 射表误差简要分析

2.1 射表误差的来源

从射表的编拟过程，可以看出射表编拟的许多环节都存在误差。这些误差产生的原因和性质如下：

由于射表符合计算的依据是距离射的结果，因而距离射结果的可信程度直接影响射表的可信程度。影响弹道的因素很多，这些因素中很多都是随机的，因而射击结果本身也是一个随机量。即便在相同射击条件下射击，每发射弹的射程也都不相同，很难肯定该射击条件下的准确射程究竟是多少。在射击试验中通常是取该射击条件下所有各发弹射程的平均值作为射击结果，但这只是一种估值方法。结果的可信程度取决于射程散布的大小和射击发数的多少。散布越大，则该结果的误差越大；而射击发数越多，则结果误差越小。所以散布越大，所需射击的发数愈多。

设相同条件下射击n发弹，其散布（即射程的概率误差）为Bχ，则其平均值作为射程的估计误差为：

设不同条件下射击m组，每组n发，则射击总发数为m×n。若其平均散布为Ex，则m组总平均值的随机误差（由随机误差引起的射表误差）为：

除了射击结果的随机误差外，初始条件的测量误差也是随机的。例如初速测量的随机误差，使所测出的初速不能完全反映真实的初速，这也能影响符合计算的结果，因而影响表定初速下的射程。掷角测量的随机误差也有同样的作用。这些误差的大小都与射击发数的多少有关。

2.2 当日误差

试验条件的误差对当天的试验结果能产生系统误差。例如试验时气压测量偏高，也就是实际气压低于测量值，则实际射程将大于计算射程。如果将实测射程换算到标准条件下，将使射程产生一个正误差。因为这次试验气压测量的都偏高，所以这一误差是系统误差，不能靠增加射击发数来减小当日误差。但如果在不同日期反复试验，每次实验条件下的测试误差不可能是相同的，所以当日误差就成了随机性的。求出不同日期试验结果的总平均值作为试验结果，即可减小当日误差的影响。

设在不同日期共试验m组，每次的当日误差为εx，则由当日误差引起的射表误差为：

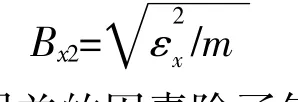
引起当日误差的因素除了气象条件的测试误差外，还包括跳角的误差等。跳角的大小与很多因素有关。由于每次试验时火炮的支撑情况不可能完全相同，因而跳角必然有误差。现在还无法在距离射的同时测跳角，只能用弹道射时的跳角来代替，因而将产生系统误差。如果在不同日期反复试验，即可减小跳角的系统误差。此外初速测量除了有随机误差外，也存在当日误差。

2.3 模型误差

数学模型的误差主要来自建立运动方程时所作的假设。这些假设程度不同地都将造成弹道计算误差。

如果距离射只在一个射角下进行，经过符合计算后在该试验射角下模型误差已不存在。但在利用符合计算结果计算其他射角时，模型误差就会出现。这时模型的优劣将起很大作用。

如果距离射在几个射角下进行，这时模型误差主要体现在c～θ0曲线的拟合误差上。模型误差越大，则c随θ0的变化越大，变化的规律性也越差，因而曲线拟合的误差也越大。经验表明，利用同样的符合计算结果作支撑点，用不同的拟合方法所得的c～θ0曲线计算出的射程是有明显差别的。这一误差应归属于模型误差。此误差的大小与射击的组数和发数都没有关系。

2.4 射表误差的综合计算

通过以上分析，可以对射表误差有一个初步的了解。实际上误差来源可能还不止于此。但概括起来射表的误差源不外以上3种类型。

第1种是与距离射总发数有关的误差，统称为随机误差，用Bx表示。

第2种是与射击组数有关的误差，统称为当日误差，用εx表示。

第3种是与距离射的射击组数和发数皆无关的误差，统称为模型误差，用ηx表示。例如运动方程中某些原始数据，有的来自理论计算，或者来自地面试验，都有误差。此误差与距离射的组数和发数皆无关系，也可列入模型误差的范围。

综上所述，可将射表总误差用下式表示：

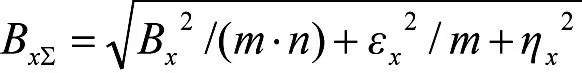
3 射表误差对射击精度的影响

对车载武器来说，使用原始火控系统条件下，当不使用激光测距仪时，目测判定距离误差是射击准备误差的主要根源，射表误差对射击准备误差的影响很小。当使用激光测距仪测距时，射击环境误差在射击准备误差中的地位显著提高，成为射击准备误差的主要根源，这时射表误差对射击准备误差的影响也不大；在使用现代火控系统条件下，随着射击环境误差的大幅减小，武器的射击准确度越来越高，武器校正和射表误差的地位越来越突出，成为影响射击准确度的主要误差根源，目前随着武器校正精度的不断提高，射击准备误差进一步减小，射表误差已成为影响射击精度的主要误差根源。因此，提高射表精度是目前条件下缩小射击误差，进一步提高射击准确度的重要途径。

参考资料：

［1］朱训慧.坦克射击学［M］.蚌埠：蚌埠坦克学院出版社，1995.

［2］宋丕极.枪炮与火箭外弹道学［M］.北京：兵器工业出版社, 1993.

［3］赵成吉.射击外弹道学［M］.沈阳：沈阳炮兵学院出版社，1987.

Influence Analysis of Firing Table Error and for Fire Accuracy

ZHU Xun-hui，ZHAO Jian-kang，YAN Hao
（Armored Force Academy，Bengbu 233050，China）

Taking the vehicle mounted weapon as research object，the function and basic requirement of the firing table is definitized，the compositive factor and brief calculating methods is analysed.Based on this，the influence that the firing table error and for fire accuracy is analysed. Meanwhile，the perspective that the firing table error is the mainly influencing factors to the fire accuracy of vehicle mounted weapon，and it provides statedly reference to the reaserch of the fire accuracy of vehicle mounted weapon.

vehicle mounted weapon，firing table error，fire accuracy

E920.2

A

1002-0640（2015）05-0128-03

2014-03-07

2014-04-24

朱训慧（1956- ），男，山东淄博人，教授，硕士生导师。研究方向：军事装备学，坦克射击。