任意分布随机数的FPGA实现

王 菊，王和明，徐海龙，丁 浩

（空军工程大学防空反导学院，西安 710051）

任意分布随机数的FPGA实现

王 菊，王和明，徐海龙，丁 浩

（空军工程大学防空反导学院，西安 710051）

为了满足数字电路板的随机测试需求，在Simulink/DSP Builder中建立了产生任意分布随机数的模型,并在FPGA上进行了半实物仿真和性能分析，结果表明该模型达到了设计要求，具有实用价值。

半实物仿真，任意分布随机数，Simulink/DSP Builder，FPGA

0 引言

数字电路板的测试矢量生成一直以来都是测试中的难点。为了对一个有n输入端的数字电路板进行完备测试，一般情况下需要施加2n组输入矢量，但当n较大时，这是不可实现的。针对目前的研究现状，一种比较快速的测试方法就是随机测试。

本文针对数字电路板的随机测试需求，在Simulink/DSP Builder中建立了任意分布随机数的模型，并利用Signal Complier模块转换为QuartusII的工程，在FPGA中得以实现。

1 随机数产生的原理

除了少数算法之外，大部分的算法都是通过函数映射或者转换来实现的，这些算法的实现前提是需要有一组满足质量要求的均匀随机数。因此，研究任意分布随机数的FPGA实现，首先要解决的问题是如何产生一组均匀分布的随机数。

1.1 均匀随机数产生原理

均匀随机数就是在某个区间内任何一点出现的概率是相等的，没有规律可循，无法根据前一个数据推算出下一个数据。产生均匀分布随机数的一般方法有迭代取中法、乘同余法和混合同余法。由于迭代取中法的一个显著不良特性就是比较容易退化成0，乘同余法产生的随机数不够均匀，因此，本文中采用统计特性较好，速度较快的混合同余法来产生均匀随机数。

混合同余法又称线性同余法，产生随机数的递推公式为：

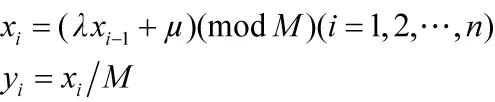
式中，λ（0＜λ＜M）、μ（0≤μ＜M）和M分别是乘数、增量和模，这3个参数的选取对均匀随机数的质量有较大的影响，一般M=2q，λ=2c+1（c≈q/2），/M，i=0时的x0称作种子。产生随机数xi的最大可能周期为M，对任一周期内的数据用M进行归一化即可以得到分布于（0，1）区间内的均匀随机数yi。

1.2 任意分布随机数产生的原理

在产生均匀随机数的基础上，通过变换和函数映射可得到任意概率分布的随机数，主要方法有反函数法、变换法和舍选法。反函数法是求任意概率分布的一种常用的方法，采用这种方法的一个明显局限就是分布函数F（x）必须是可逆的。变换法是通过一个变换将一种分布的随机数变换成不同分布的随机数，但是由于这种方法必须要找到一种分布和另一种分布之间的映射关系而不具有普遍适用性。舍选法适合用FPGA高速实现，因此，本文中主要利用这种方法实现任意概率分布的随机数。

舍选法是冯·诺曼为克服反函数法和变换法的困难最早提出来的。其基本思想是按照给定概率密度函数f（x），对均匀分布的随机数u进行舍选，舍选的原则是在f（x）大的地方，保留较多的随机数，反之保留较少的随机数，其示意图如图1所示。

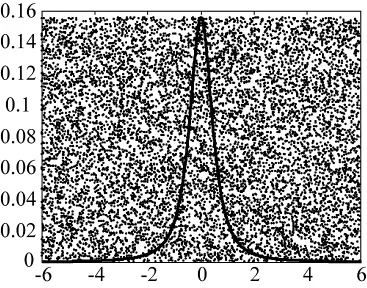
图1 舍选法示意图

该方法产生随机数的具体做法是在oxy平面上等概率的随机产生一个矩阵区域的随机点，只保留概率密度曲线下方的点，此时概率密度曲线下方的点的个数是服从给定概率分布的，需要产生的随机数就是这些点的横坐标。

2 随机数的FPGA实现

2.1 均匀随机数的FPGA实现

在Simulink/DSPBuilder中建立模型，如图2所示。

其中，a和b分别表示均匀随机数产生区间的下界和上界，核心模块是Embedded MATLAB Function，该模块的内部是用S函数编写的混合同余算法，由于该模块的输出是一个一维数组，无法直接用IO端口读出，因此，本文选择将数组导出存入到ROM中，随着地址依次增加将数据读出。添加必要的数据转换模块和输入输出模块，利用Signal Complier将Simulink/DSP Builder中的模型转换为QuartusII的工程文件，编译该工程，得到的仿真波形如图3所示。

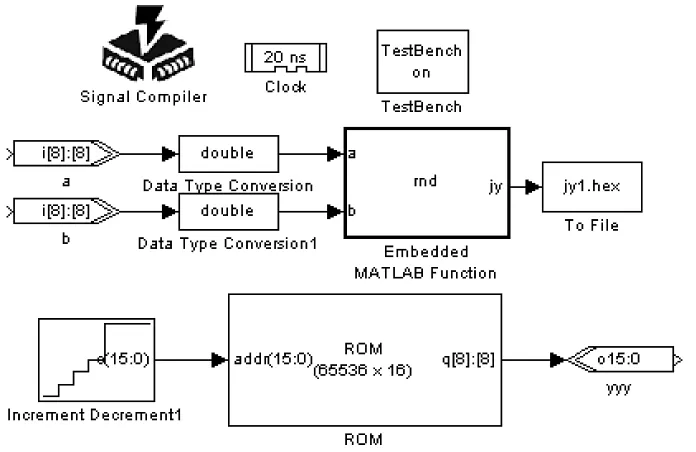
图2 均匀随机数产生模型

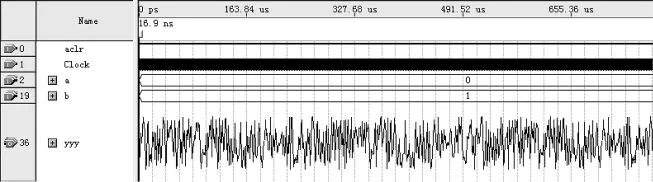
图3 QuartusII中均匀随机数的仿真波形

2.2 任意分布随机数的FPGA实现

在FPGA上实现舍选法时，具体的做法是首先产生［a1，b1］均匀随机数u1和［a2，b2］均匀随机数u2，若u2＜f（u1），则输出u1，否则u1被拒绝。在Simulink/DSP Builder中建立的舍选法模型如图4所示。

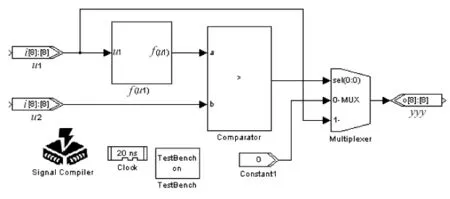
图4 舍选法模型

模块f（u1）是所要产生的概率密度函数，根据需要设置该模块中的函数，本文中以在［1，2］区间内产生概率密度函数为f（x）=2（1-1/x2）的随机数为例。从u1和u2端口输入的信号即是用第2节中的模块产生的在［a1，b1］和［a2，b2］区间内的均匀随机数，剔除不必要的零点，在QuartusII中任意随机数产生的整体模型如下页图5所示。

图中jy_exzample和sc_exzample分别是由均匀随机数产生模型和舍选法模型生成的在QuartusII中的子模块，编译后的仿真波形如图6所示。

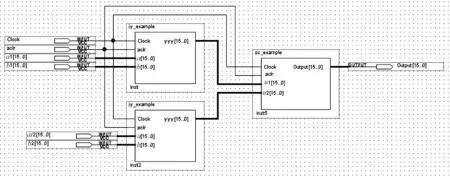
图5 QuartusII中任意分布随机数产生整体模型

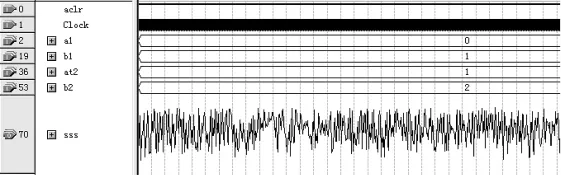
图6 QuartusII中f（x）=2（1-1/x2）的随机数仿真波形

3 性能分析

通过混合同余法和舍选法，用FPGA实现了任意分布的随机数，本文从半实物仿真结果和概率统计结果两个方面对生成的随机数性能进行分析。

3.1 半实物仿真分析

在QuartusII中尽管获得了全硬件的仿真结果，但是由于没有了MATLAB的强大仿真工具，一些特定功能的激励信号难以获得，很多希望的仿真结果比较难以实现。因此，理想的方法就是在Simulink平台上将设计模型下载进FPGA，利用Simulink提供的各类仿真工具进行仿真［3］。

通过DSP Builder提供的HIL（Hardware in the Loop）模块，利用DE2开发板，得到的半实物仿真波形如图7所示。

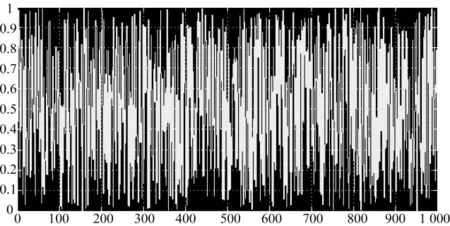
（a）均匀随机数半实物仿真波形

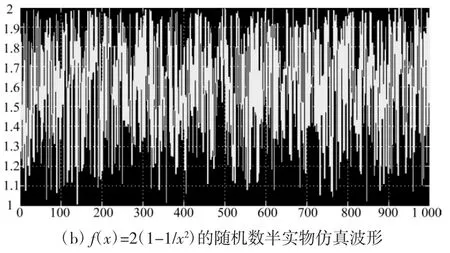
图7 生成随机数的半实物仿真结果

对图3、图6和图7进行比较可以得出：仿真结果和半实物仿真结果具有很高的一致性，达到了设计目的。

3.2 随机数分布统计分析

利用半实物仿真得到结果的是随机数和时间的变化关系，从波形中很难看出所得随机数的分布性能，因此，利用MATLAB中的概率统计函数，对所得均匀随机数的分布性能进行分析，得到随机数分布情况如图8所示。

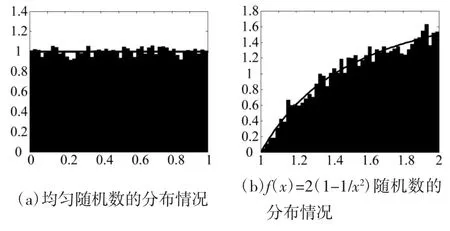
图8 生成随机数的分布情况

从图8中可以得出：虽然均匀随机数和概率密度函数为f（x）=2（1-1/x2）随机数分布的上边界不是十分平坦，但是已经基本吻合了其概率密度函数，达到了设计要求。

4 结论

本文首先利用混合同余法实现了均匀随机数，然后利用舍选法实现了概率密度函数为f（x）=2x的随机数。事实上，在Simulink/Dsp Builder中设置不同的概率密度函数，就可以产生相应分布的随机数，可以应用于数字电路板的随机测试，具有实用价值。

采用在Simulink/Dsp Builder中建立相应算法的模型，然后利用Signal Complier产生QuartusII中工程的这种方法，既具有了MATLAB的强大的计算功能，Simulink齐全的仿真工具，又能将其在硬件上实现，是一种简化硬件实现过程的有效方法。然而这种方法的一个不足就是会占用大量的芯片资源，在使用中应尽量简化模型，降低所占资源的数量。下一步将致力于如何简化模型，并建立任意波形产生的模型。

［1］宋克俭，杨军.基于FPGA的快速均匀分布随机数发生器［J］.云南大学学报（自然科学版），2007，29（S2）：279-282.

［2］朱晓玲，姜浩.任意概率分布的伪随机数研究和实现［J］.计算机技术与发展，2007，17（12）：116-118.

［3］潘松，黄继业.EDA技术与VHDL［M］.北京：清华大学出版社，2009.

［4］曾治丽，李亚安，金贝立.任意分布随机序列的产生方法［J］.声学技术，2010，29（6）：651-654.

［5］杜学峰，武杰.基于FPGA的任意分布高速伪随机数发生器［J］.中国科学技术大学学报，2006，36（9）：990-993.

［6］谷晓忱，张民选，一种基于FPGA的高斯随机数生成器的设计与实现［J］.计算机学报，2011，31（1）：165-172.

［7］祝爱民，石春和，董良东，汪君华.基于FPGA高斯白噪声发生器的设计与实现［J］.火力与指挥控制，2009，34（7）：119-121.

Realization of Arbitrary Distribution Random Number Based on FPGA

WANG Ju，WANG He-ming，XU Hai-long，DING Hao
（The Missile Institute，Air Force Engineering University，Xi'an 710051，China）

In order to meet the demand for random test of digital circuit board，this paper establishes the arbitrary distribution random number model in Simulink/DSP Builder，the semi physical simulation and the analysis of performance are tested on the FPGA，the results show that the model can meet the design requirements and has practical value.

semi physical simulation，arbitrary distribution random number，Simulink/DSP Builder，FPGA

TN911

A

1002-0640（2015）04-0173-03

2014-01-05

2014-03-07

王 菊（1991- ），女，陕西西安人，硕士研究生。研究方向：微电子技术应用。