基于移相器控制电压的“动中通”波束形成改进算法*

任肖丽，衷惟海，王 骥，万 群

（1.广东海洋大学信息学院，广东 湛江 524088；2.解放军92619部队，广东 深圳 518000；3.电子科技大学电子工程学院，成都 611731）

基于移相器控制电压的“动中通”波束形成改进算法*

任肖丽1，衷惟海2，王 骥1，万 群3

（1.广东海洋大学信息学院，广东 湛江 524088；2.解放军92619部队，广东 深圳 518000；3.电子科技大学电子工程学院，成都 611731）

在波束形成技术中，基于同时扰动随机梯度估计算法计算接收功率对移相器控制电压的梯度，研究了同时扰动随机梯度估计算法中扰动量和电压更新方程中步长的取值问题。仿真结果表明，随迭代次数变化的扰动量较固定扰动量能有效地提高算法的收敛性能，在同时扰动随机梯度估计算法中，将步长改为随阵元空间位置变化，能有效地提高电压更新方程的收敛速度。研究了与变扰动量有关的参数取值，指出了参数的选取准则。MATLAB仿真结果验证了所改进算法的正确性和有效性。

波束形成，“动中通”，同时扰动随机梯度估计算法，扰动量，步长

0 引言

卫星通信是一种重要的无线通信方式，卫星通信具有覆盖范围广、通信质量好、不受地理条件限制、信道稳定、适应性强等优点，具有广阔的应用前景［1-4］。但是传统的固定卫星通信系统要求载体只有在静止条件下才能与卫星进行通信，一般不具有无线通信系统可在运动中实现实时通信的能力。为了解决“运动中稳定卫星通信”这一问题，“动中通”技术由此产生。早在 1984年和 1988年，P.A. Matthews和David Shaw就提出了“动中通”系统的思想［5-6］。“动中通”卫星通信系统通常安装在汽车等移动载体上，通过自动调整自身姿态自动跟踪卫星进行实时通信。“动中通”主要思想是要构造一个稳定平台，使运动载体上的天线不受外界扰动影响，即使天线的空间指向相对于工作卫星其指向不变［7］。

目前，国内外有很多讨论“动中通”系统的文献，其中有介绍“动中通”产品的文献［8-10］，对于相控阵天线“动中通”系统波束形成技术，文献［11］采用双边扰动算法求解接收功率对控制电压的梯度，文献［12］对双边扰动梯度估计算法和同时扰动随机梯度估计算法进行了对比，前一种算法收敛需要较少的迭代次数，而后一种算法具有较短的收敛时间。本文研究“动中通”系统中的波束形成追踪问题，采用收敛较快的同时扰动随机梯度估计算法，改进该算法为变步长与变扰动量，并对改进后算法的收敛性能进行了仿真分析。

1 问题描述

Mohammad Fakharzadeh Jahromi［11，13］给出的问题描述为：

其中，P为天线的接收功率，w为天线的权矢量，R为接收数据的协方差矩阵，Rs为信号分量的协方差矩阵，ρ为接收信号的信噪比（SNR），σn2为噪声功率，vi为各天线阵元上的控制电压。

电压更新方程为：

2 同时扰动随机梯度估计算法

Spall［14-16］对同时扰动随机梯度估计算法进行了深入的研究，通过扰动测量值以获得梯度估计。

通过Monte-Carlo方法产生一个p维的随机扰动矢量△k。对于△k中的p个元素是采用概率为0.5的伯努利分布产生，使它的取值为+1或-1。通过下式完成对梯度的估计：

其中，k为迭代次数，△ki为△k的第i个元素，ck为扰动量。

由

完成对变量的更新，满足条件时，终止迭代［18］。

3 改进算法

对于一个移动平台，为了避免接收信号功率明显下降，对于N个阵元中的每个阵元都应满足，其中波数。则

其中，xi为第i（1≤i≤N）个阵元相对于参考阵元的位置。

由式（2）、式（5）知，移相器的控制电压与相位相对应，因此，将对电压的调整转化为对相位的直接调整，即

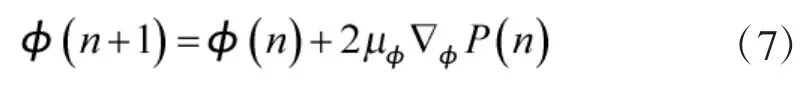
对于一个N元均匀线阵。接收信号功率为：

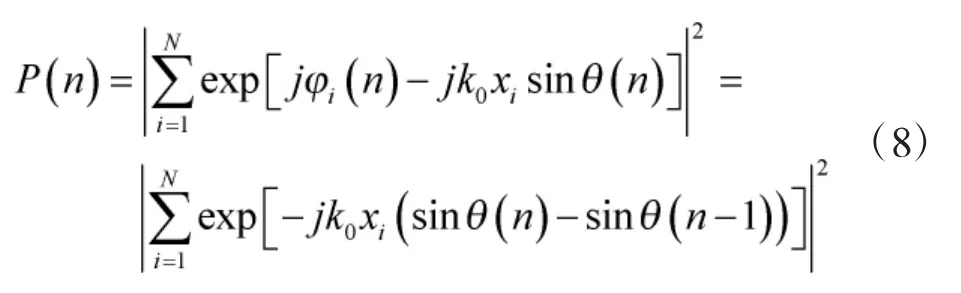
由于

其中，△i（n）表示△（n）的第i个元素。

于是

令

则

假设以最左边的阵元作为参考0阵元，则有

则

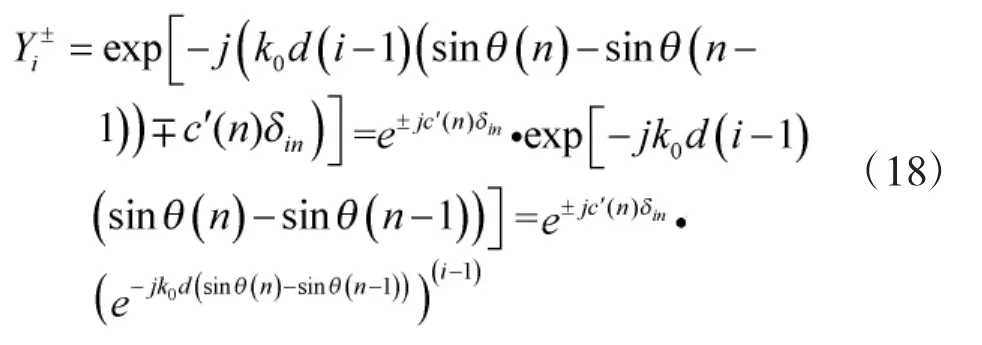
3.1 扰动量的选取

文献［14］给出的c（n）的表达式为：

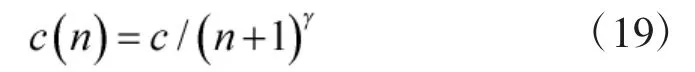
其中，c和γ为常数，n为迭代次数。对于参数c的选取，尽量选择c小于等于y（θ）中噪声的标准差，以使得中的p（p=N）个元素在幅度上不会太大。大量试验表明，低信噪比时所确定的较大c值也适用于高信噪比，且收敛性能也有所提高，在实际中，确定c值应考虑环境信噪比和梯度幅度大小。参数γ通常取为小于渐进最优值γ=1/6的正常数。

3.2 步长的选取

为了满足前面给出的线性阵列运动过程中的收敛条件，要求n+1时刻未知DOA的波束形成算法能够补偿n-1时刻与n时刻的接收功率的相位变化，即：

又由式（7），可得

因此，有

将式（17）代入上式，有

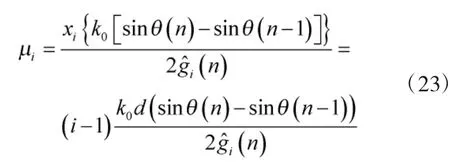
令

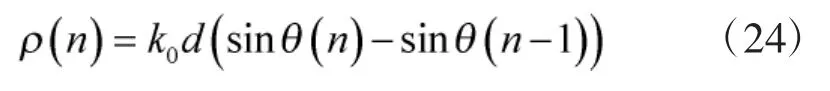
对于移动的波束形成而言，ρ（n）依赖于角速度和算法的执行时间△T，由于算法执行时间非常短，则有，再根据三角函数和差化积公式，经适当近似可得

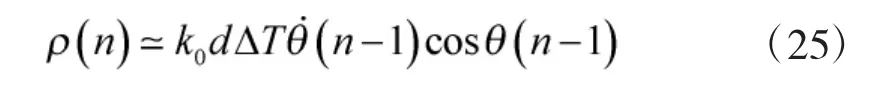
对于一个移动阵列，μi依赖于阵元的位置xi，随角速度的增加而增大；随波束形成速度的增加而减小。

4 仿真验证

文献［19］给出的悍马越野车最大角速度和最大角加速度数据表明，悍马车的最大角速度为84.6°/s，最大角加速度为729.2°/s2，且要求追踪精度≤0.5°［20］，由此假设电压更新时间间隔为△t=0.5/ 84.6s=5.9ms。在功率更新的过程中，假设在t=187.6ms的时候出现了最大角加速度（总仿真时间约为0.4s），则△v=729.2°/s2×0.005 9 s=4.302 3°/s，则加速后的角速度为v'=84.6+4.302 3=88.920 3°/s。由加速度公式 2as=v'2-v2，得在 △t=5.9 ms内改变的角度为0.514°。设初始电压为v=4 V（假设电压变化范围为0～8 V），初始来波方向为θ=0°。作下页图1仿真，其中c=0.1，μ=0.005，SNR=20 dB，噪声为均值为零的高斯白噪声。

由图1可知，天线不能追踪到运动车辆的信号方向改变，在△t=5.9 ms内，天线接收到的功率不能达到最大功率值，由于随着这种误差的积累，导致波束完全丢失目标。

图1 波束追踪能力仿真图

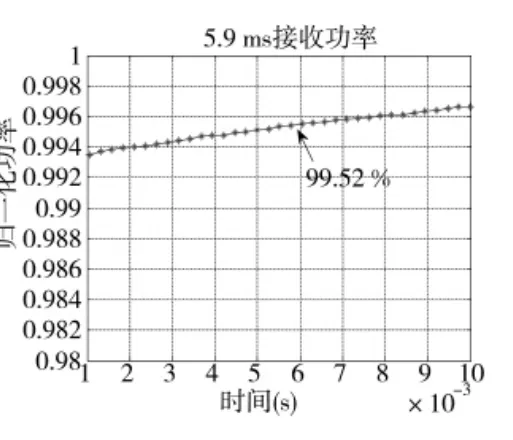
图2 内波束追踪功率变化仿真图

事实上，在△t=5.9 ms内，波束只能追踪到99.52%的最大接收功率，如图2示。由此可知，在△t=5.9 ms的迭代时间内，波束不能完全追踪到信号方向的变化，应该改进算法，使算法在短的时间得到收敛。否则，随着这种功率误差的累积，将导致目标丢失。

4.1 变扰动量

选取c=0.1，γ=0.01，SNR=20dB，仿真如图3所示。

图3 修正扰动量后5.9 ms内追踪功率变化仿真图

图4 扰动量与步长联合修正后5.9 ms内波束追踪功率变化仿真图

由图3可知，适当选择c和γ能够改变收敛性能。上文中已经阐明，如果采用固定扰动量c（n）=0.1，在5.9 ms内只能追踪到99.52%的最大功率，而修正扰动量后，则可以追踪到99.90%的最大功率。c和γ的最优值需要通过大量的实验验证才能得到。

4.2 变步长

从图4中可以看出，经过扰动量和步长调整（步长μi=0.005+（i-6）×0.000 6）之后，在5.9 ms之内，波束能够追踪到100%的最大接收功率，而采用随迭代次数变化的步长，则不能完全追踪到波束的变化，只能接收到99.82%的功率，而且功率变化曲线较平坦，即收敛较慢。仿真中，步长变化公式为μn=a/（A+n+1）a，其中a=0.08，A=100，α=0.602，n为迭代次数。

因此，可以得到信号方向变化时，阵列接收功率的仿真图，如图5所示。

从图5中可以看出，相同的c值适用于低信噪比和高信噪比的情况，相同信噪比时，c值较大时得到的曲线更平滑，这是因为此时算法能更快收敛到最大接收功率，能对接收到的功率进行多次平均。同样看到，噪声引起接收功率产生波动。

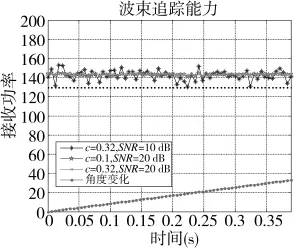
图5 修正扰动量和步长后的波束追踪能力仿真图

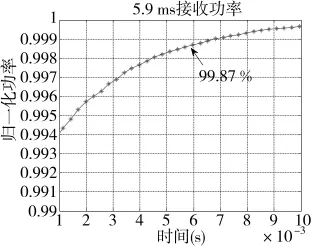
图6 角加速度时刻接收到功率的仿真图

对比图1与图6，可以得到，经过扰动量和步长的调整之后，本文提出的算法能够满足追踪精度的要求。即使在出现加速度的时刻，波束也能追踪到这一角度的变化。

事实上，对于加速度出现时刻的角度变化，5.9ms内已能追踪到99.87%的最大功率，如图6所示。

图7为本文算法与文献［11］中算法波束追踪能力的比较仿真图。其中双边序贯随机梯度估计中，扰动量δ=0.5，SNR=20 dB。

图7 与文献中方法的比较图

由图7可知，文献中的方法在△t=5.9 ms的时间里无法跟踪到角度的变化。由于文献中算法的收敛时间要比本文算法长，在△t=5.9 ms的时间里不能将移相器控制电压更新到追踪信号方向所需的电压值，随着误差的累积，导致目标完全丢失。即，文献所给出的算法，在实际使用中将不能达到本文提出算法的角速度追踪能力。文献给出的角速度为60°/s，低于本文设计的84.6°/s。

5 结论

移相器控制电压的模拟波束形成在单信号源时，波束完全对准信号源，通过直接调整移相器控制电压形成波束追踪信号来波方向。考虑到采用序贯双边梯度估计算法计算接收功率对电压梯度收敛时间较长，导致天线平台快速移动时容易丢失目标，本文采用同时扰动随机梯度估计算法计算梯度，针对该算法中扰动量中参数的选择问题，通过大量实验研究，得到了适合于“动中通”系统的参数选取准则，并改变同时扰动随机梯度估计算法原型中步长随迭代次数变化的模型，取步长随阵元空间位置变化，获得更好的收敛性能。通过仿真表明，本文算法比文献中采用的算法具有更好的收敛性能，能更好地追踪目标。

［1］郑林华，韩方景.卫星移动通信原理与应用［M］.北京:国防工业出版社，2000.

［2］王丽娜，王兵，周贤伟，等.卫星通信系统［M］.北京:国防工业出版社，2006.

［3］中国卫星通信广播电视用户通信协会.卫星通信广播导航遥感应用手册［M］.北京:中国宇航出版社，2006.

［4］吕海寰，蔡剑铭，甘仲民，等.卫星通信系统（修订本）［M］.北京:人民邮电出版社，1996.

［5］Matthews P A.Communications on the Move［J］.ELECTRONICS&POWER，1984:513-518.

［6］David S.Communications on the Move［J］.IEEE Rev.，February 1988，34（2）:83-85，18.

［7］朱军.基于GEO卫星的“动中通”系统设计与关键技术研究［D］.南京:南京理工大学，2008.

［8］Ryu M，Toyohisa T，Isamu C，et al.Beamforming Experiment with a DBF Multibeam antenna in a Mobile Satellite Environment［J］.IEEE Transactions on Antennas and Propagation，1997，45（4）:707-714.

［9］Seong H S，Ung H P，Soon I J.Mobile Antenna System for Ku-Band Satellite Internet Service［C］//The 61st IEEE Vehicular Technology Conference，30 May-1 June 2005：234-237.

［10］Mousavi P，Fakharzadeh M，Jamali S H，et al.A Low-Cost Low Profile Phased Array System for Mobile Satellite Reception Using Zero-Knowledge Beamforming Algorithm［J］. IEEE T Transactions on Antennas and Propagation，2008，56（12）:3667-3679.

［11］Mohammad F J.Optical and Microwave Beamforming for Phased Array Antennas［D］.Waterloo，Canada:University of Waterloo，2008.

［12］Fakharzadeh M，Jamali S H，Safavi-Naeini S.Fast Stochastic Beamforming for Mobile Phased Array Antennas［C］// Antennas and Propagation Society International Symposium，Honolulu，HI，2007：1945-1948.

［13］Fakharzadeh M，Mousavi P，Safavi-Naeini S，et al.The Effects of Imbalanced Phase Shifters Loss on Phased Array Gain［J］.IEEE Antennas and Wireless Propagation Letters，2008（7）:192-196.

［14］Spall J C.Implementation of the Simultaneous Perturbation Algorithm for Stochastic Optimization［J］.IEEE Trans. Aerosp.Electron.Syst.，1998，34（3）:817-823.

［15］Spall J C.A Stochastic Approximation Technique for Generating Maximum Likelihood Parameter Estimates［C］// Proceedings of the American Control Conference，1987.

［16］Spall J C.Multivariate Stochastic Approximation Using a Simultaneous Perturbation Gradient Approxi Mation［J］. IEEE Transactions on Automatic Control，1992（37）: 332-341.

［17］ Ruppert D.Kiefer-Wolfowitz Procedure，Kotz S，et al. Johnson（Eds.），Encyclopedia of Statistical Science［M］. New York:Wiley，1983（4）:379-381.

［18］Pflug G C.Optimization of Stochastic Models:The Interferece Between Simulation and Optimization［M］.Boston：Kluwer Academic，1996：297-300.

［19］Herald B，Lou C，Tat F.Army SATCOM On The Move Technology Initiatives［R］.MIT Lincoln Labs memorandum 63L-06-20，Response to Inquiry on Vehicle dynamics Measurement Campaign，2006.

［20］秦丽平，徐贵民，赵建勋，等.多板天线“动中通”跟踪测角算法研究［J］.电光与控制，2009，16（6）:86-88.

［21］Hao L Y，Yao M L.SPSA-based Step Tracking Algorithm for Mobile DBS Reception［J］.Simulation Modeling Practice and Theory，2011，19（2）:837-846.

［22］张峰干，贾维敏，金伟，等.基于同时扰动的单通道接收阵列天线跟踪方法［J］.系统工程与电子技术，2013，35（5）:1085-1090.

Research of Beamforming in“On-the-Move Communication”System Based on Control Voltage of Phase Shifters

REN Xiao-li1，ZHONG Wei-hai2，WANG Ji1，WAN Qun3
（1.School of Information，Guangdong Ocean University，Zhanjiang 524088，China；
2.Unit 92619 of PLA，Shenzhen 518000，China；
3.School of Electronic Engineering，University of Electronic Science and Technology of China，Chengdu 611731，China）

In the beamforming technology，the gradient of the

power to the control voltage of the phase shifter based on simultaneous perturbation stochastic algorithm（SPSA）is estimated.The values of disturbance in SPSA and step-size in voltage updated equation is mainly studied.Research found that when the disturbance changes with the iteration times can effectively improve the convergence performance of SPSA compare to when use a fix disturbance，and compare to changes with the iteration times，a variable step-size with the space of elements but with the iteration times which is proposed in the basic model is useful to improve the convergence performance of voltage updated equation.And the value of parameters related to the variable perturbation is also studied，and pointed out the parameter selection criteria.MATLAB simulation results demonstrate the validity of the theoretical analysis and the efficiency of the algorithm.

beamforming，on-the-move communication，Simultaneous Perturbation Stochastic Algorithm（SPSA），perturbation，step-size

TN911.7

A

1002-0640（2015）04-0018-05

2014-04-05

2014-04-19

国家自然科学基金（60772146）；国家“八六三”高技术研究发展计划（2008AA12Z306）；教育部科学技术研究重点项目（109139）；广东省自然科学项目（S2012010008261）；广东海洋大学创新强校工程科研基金资助项目（GDOU2013050232）

任肖丽（1982- ），女，辽宁朝阳人，硕士，实验师。研究方向：阵列信号处理等。