给水度与水位埋深的关系及其测定与应用

李 虹

（辽宁省沈阳水文局，沈阳110043）

技术论坛

给水度与水位埋深的关系及其测定与应用

李 虹

（辽宁省沈阳水文局，沈阳110043）

土层的给水度是平原潜水区的水资源计算的重要参数，从能量守恒定律的观点系统分析“水转化”的成因规律，进一步认识土层水运动形态，用实验的方法确定土层的给水度，这是撰此文追求的目的。为此，明确了随着水位埋置深度的变化，含水层的给水度变化的特点，并且运用土质水分运动模拟地下水动态，推求降雨入渗补给和水蒸、散发量的方法。

给水度；毛管强度；水位埋深；降雨入渗；水分运动

1 地下水埋深与给水度关系

给水度是指含水层的释水能力。它表示单位面积的含水层，当潜水面下降一个单位长度时在重力作用下所能释放出的水量。地下水埋深指地下水到地表的距离，地下水浅埋深的变化反映着地下水包气带中由于植物根系蒸发蒸腾、潜水面的蒸发，地表和地下径流引起的水分通量的变化。当水位降深小于毛细上升高度时，给水度较小，并随着水位降深的增加而增大。当水位埋深大于毛细上升高度时，给水度由毛细上升高度段及毛细上升高度以上段组成。毛细上升高度段，给水度随着水位降深的增加而增大，给水度较小。而毛细上升高度以上段，给水度较大，并随着水位降深的增加趋于定值［1］。

2 不同埋深时的给水度分析

对于均质的各个同性含水层，潜水位埋深埋大时，且变化稳定，即潜水位下降过程中假设没有作物蒸腾或土壤蒸发，同时又没有地表水的渗入影响。潜水面延至地面的单位水平面面积的土柱汇总水分布曲线是一条稳定的曲线，见图1。

图1 潜水位浅深埋时均质含水层给水度计算简图

图1中显示潜水位下降前，t时刻的潜水面以下的含水层共含水达到饱和（容积）湿度为（Cs），潜水面以上，在吸力的作用下，包气带水分分布曲线是a、b、c、d、g形状，b点含水量达田间（容积）持水量（C。）。若因开采或蒸发导致潜水位下降△H，经过一定时间后，那么，t时刻潜水面以上的包气带中所形成的稳定的水分分布曲线就是a、b、e、f、g形状，e点含水量达田间持水量C。潜水位下降△H深度时，潜水面延至地面的单位水平面积土柱中所排出的水体积，就为图中两条曲线所夹的阴影面积bcdgfe乘以单位水平长度（所构成的曲面柱体所排出的水体积）。由于均质各间同性含水层，bcd与efg两条稳定的水分分布曲线形状相同，仅是平行下移了△H，所以，图中bcdgfe阴影面积与图中长方形hdg之面积相等，则所排出的水体积△W又为：

则给水度μ；

即，一般表示为△W＝μ·△H

当潜水位埋深小时，情况就不同了，在地表或邻近表层处的土壤湿度往往大于野外容水度C。水分分布曲线如图2所示：

图2 潜水位浅深埋时均质含水层给水度计算简图

经过一段时间，潜水位自埋深H，下降了△H深度，潜水位延至地面的单位水平面积的土柱所排出的水体积△W，等于图上两条水分分布曲线所围的阴影面积adgfk乘以单位水平长度（所构成的曲面所排出的水体积）。由于曲线ad与kfg是在同一个均质含水层中的稳定的水分分布曲线，仅是潜水位的位置不同，所以都可用C（Z）来表示，则

3 土壤水分特征曲线计算模型

3.1 应用经验公式

采用的应用经验公式为C（Z）＝CS·E·P（K· Z），设F（Z）为被积函数C（Z）图2的原函数，即：

3.2 扩散系数和渗透系数

在潜水位以上的包气带中，非饱和流的达西定律为：

H＝-Φ＋Z（坐标原点设在潜水位上，纵横坐标Z朝上为正）

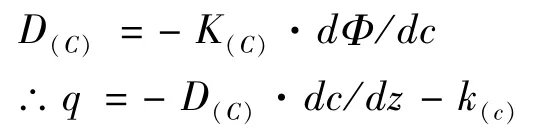
Z＝0处：C＝Cs，Z＝Z处：C＝Cz，当处在无蒸发、入渗的稳定状态下：

且D（c）＝Ds·（C／Cs）∧α

则Z＝Cs／（α-β＋1）·Ds／Ks｛1-（C／Cs∧（α -β＋1））

在自然状态下，邻近地下水位处存在着截留空气的残余饱和度；受渐变进气的影响，使C（z）曲线在接近饱和区段有一拐点（拐点为0），拐点以下曲线段为一抛物线型。

设Wぃ紺／Cs，W0、Q0为拐点处饱和度吸力，当W≤W0时，C（z）表达式采用上面的推导式。当R0≥W≥W0时，R0为地下水位处土壤水分饱和度：

那么，就可以利用数值积分计算潜水位于同埋深时，不同地下水位降幅的给水度值。

以上各式：

C（z）为距潜水位Zm处，在稳定状态时的容积；CS为均质含水层的饱和（容积）持水量；R为饱和（容积）持水量的修正系数，即CS·R表示潜水处的土壤持水量；R0为地下水位处土壤永分饱和度；H为初始潜水位埋深，m；△H为潜水位下降的变幅，m；K为土壤水分特征曲线经验的消退指数；Z为计算点距潜水位的距离；q为包气带中的土壤水通量；Φ为吸力，cm；m、n为经验参数；D（c）为非饱和土壤的扩散系数；Ds、α为经验系数和指数；K（c）为非饱和土壤的渗透系数经验式，Ks、β为经验式的系数和指数。

4 应用举例分析

4.1 应用经验公式计算

已知一种机械组成的均匀的壤土，容重1.336 g／cm3，在稳定状态时，距地下水位不同高度处的持水量计算见表1。

表1 距地下水位不同高度处的持水量计算表

该种土壤的土壤水分特征曲线经验式为：

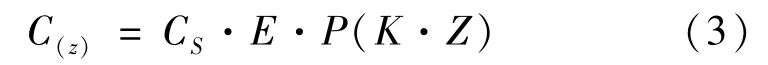
式中：CS＝0.334，占干土重百分比；K＝-2.12687E-0.1

化成线性回归时的相关系数为-0.97838，剩余标准差为0.04268。

利用上述数值可分别计算不同地下水位埋深、不同地下水位降幅的给水度。设该种土壤产生重力释水时临界土水势为0.1巴（即102cm2水柱），计算结果见表2。

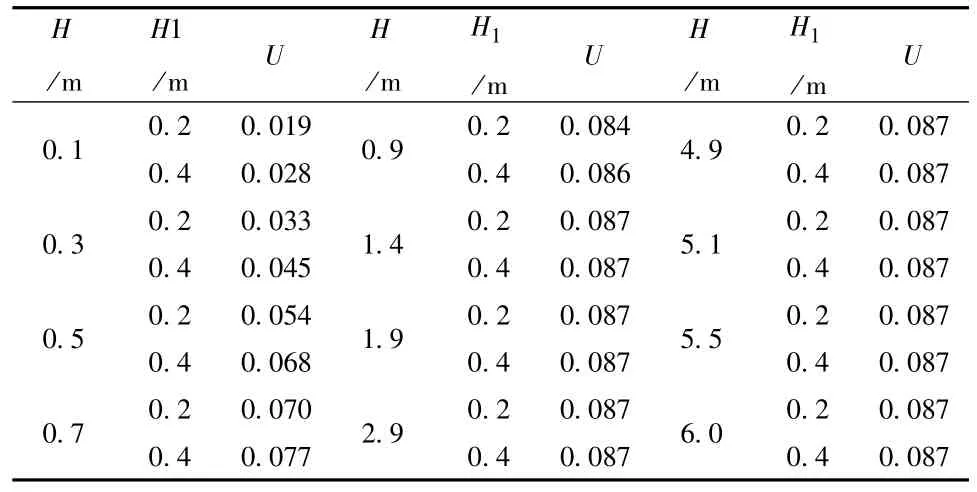
表2 不同地下水位埋深、不同地下水位降幅的给水度计算表

4.2 非饱和土壤扩散系数和渗透系数计算

某地的砂壤土，容重1.4，孔隙度0.48，以空隙度为完全饱和持水量时，土壤水分的特征曲线参数值为：

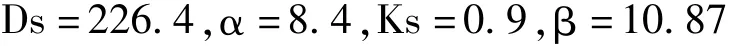
设地下水位处土壤持水量饱和度为0.83，进气点饱和度为0.83，进气点饱和度为0.8，在正常大气压下，释放重力水的临界面土水势接近0.06巴；即相当于田间持水量达0.329（容积比）推求地下水位埋深10㎝时，不同降深的平均给水度。详细数据见表3。

表3 地下水位埋深10cm时不同降深的平均给水度表

5 分析结论

通过对以上综合分析，可以得出给水度与水位埋深的关系如下：

1）当水位的埋置深度，大于该含水层的粒度所决定的毛管强度作用高度时，给水度随水位埋深的增加而很快趋于定值，即等于（经修正的）饱和（容积）持水量的田间（容积）持水量之差。

2）当水位的埋置深度，小于或等于该含水层的粒度所决定的毛管强烈作用高度时，给水度将随水位埋深的增加而增大，一般呈指数关系增大。

3）对于非均质层状含水层，利用上述原理和方法，同样可以计算不同水位埋深和不同降深的给水度。

4）运用土质水分运动模拟地下水动态，推求降雨入渗补给和水蒸散发量，其方法简便。

［1］梁宗仁.地下水浸没临界埋深问题探讨［J］.水利规划与设计，2006（05）：27-28＋60.

Relationship between Recharge Degree and Buried Depth of Water Level and Its Measurement and Application

LI Hong

（Shenyang Hydrological Bureau，Liaoning Province，Shenyang 110043，China）

The recharge degree of earth layer is an important parameter to calculate water resources of water-table aquifer in the plain，the formation of water transformation is analyzed in the paper based on the viewpoint of energy conservation law，recognizing in further the water movement state of earth layer，determining the recharge degree of earth layer through the method of experiment，it is the purpose for writing the paper.Therefore，the characteristics of recharge degree of moisture aquifer with the change of buried depth of water level are determined，and the moisture movement of earth quality is used to simulate the groundwater dynamic，so as to calculate the recharge of rainfall seepage，evaporation and thermal quantity.

recharge degree；capillary strength；buried depth of water level；rainfall seepage； moisture movement

P641.8

A

1007-7596（2015）07-0006-03

2015-06-28

李虹（1966-），女，辽宁沈阳人，工程师，主要从事水文水资源、人事管理工作。