球形容器无模爆炸成形研究

文／佟铮·内蒙古工业大学

球形容器无模爆炸成形研究

文／佟铮·内蒙古工业大学

佟铮，教授，主要从事工程爆破理论与技术的研究，中国工程爆破协会常务理事，中国爆破行业专家委员会委员，主持完成了国家自然基金、产学研重点项目、水利部项目等多项课题，曾获内蒙古科技进步二等奖、国家“八五”技术成果奖、中国爆破协会科技进步二等奖等奖项。

球形压力容器在石油、化工和造船等领域应用广泛，又称球罐。其工作压力一般均低于3MPa，在特殊情况下也可高达100MPa。它是贮存和运输各种气体、液体的一种有效、经济的压力容器。与圆筒形容器相比其主要优点是受力均匀，在同样壁厚条件下，球罐的承载能力最高。在相同内压条件下，球形容器所需要壁厚仅为同直径、同材料的圆筒形容器壁厚的1/2；在相同容积条件下，球形容器的表面积最小。由于壁厚薄、表面积小等原因，一般要比圆筒形容器节约30%～40%的钢材。在制造工艺方面，这类容器所需要的钢种大多为低合金钢，其焊接性一般较差，故须采取可靠的焊接工艺措施。球形压力容器由多块球瓣拼焊而成，须严格保证各球瓣尺寸精度，以防止在球壳局部产生过高的附加应力。很多球形压力容器因体积大，只能在现场拼装焊接，需要更为严格的现场施工质量管理。

爆炸成形是利用炸药爆炸所产生的爆炸冲击载荷和高压气体的膨胀作用，通过传压介质将能量传递到金属坯料上，使金属坯料产生塑性变形，并达到图纸要求的形状、尺寸、精度和表面光洁度，从而获得所要求的零部件。本文通过内蒙古工业大学为某啤酒厂无模爆炸成形球形容器为实例，着重介绍了球形容器的无模爆炸成形原理、参数设计以及有限元数值模拟。

球形容器无模爆炸成形原理

图1 四节锥台壳体结构示意图

球形容器无模成形原理是预先卷制两节以上球内接多节锥台壳体（图1为四节锥台壳体结构示意图），外接球直径为球体设计直径D，并与上下圆形极板组焊成球内接密闭壳体，其中极板直径d需与锥台母线长度a保持一致。为便于向壳体内注水以及放置炸药，须在上极板中心处开设中心孔。当起爆球形药包置于水中球心处时，水中产生的球面冲击波首先冲击锥台侧面及上下圆形极板距球心最近部分。由于球面冲击波的能量密度与传播距离大致按平方关系进行衰减，而且冲击波的峰值压力也随传播距离的增大而减小，因此造成壳体板料各质点的运动速度矢量差，使锥台壳体不断向外接球面靠扰。通过控制球心处球形炸药包能量的大小，可实现锥台壳体的变形恰好达到消除锥台直边及上下极板的直边，当壳体的直边部分完全与外接球面重合时，便完成了球壳无模成形的全过程。锥台壳体上各条环向焊缝均处在外接圆上，所以各条环向焊缝未发生变形。球形容器无模爆炸成形原理示意图，如图2所示。

图2 球形容器无模爆炸成形原理示意图

预制锥台壳体设计

多节圆锥台壳体是球壳无模成形前的最佳预制壳体结构。预制壳体设计必须遵循的两条基本原则是：⑴多节圆锥台壳体应为直径为D的球内接壳体；⑵每节锥台母线长度a应和上下圆形极板的直径d相等。各节锥台均由扇形板料卷制而成，当壳体总节数为奇数时，赤道带为一由矩形板料卷制的圆筒。表1为不同锥台节数N值对变形参数影响。

表1 不同锥台节数N值对变形参数的影响

锥台壳体变形能与药量关系

根据米塞斯（Von.Mises）屈服准则，在比例加载条件下，金属壳体总应变能包括各节锥台应变能及上下圆形板应变能。根据锥台壳体胀形为球壳所需要的塑性变形能，以及壳体内悬置中心药包传递给壳体的有效能量，球形容器无模爆炸成形的中心药包最小药量与材料、壳体结构、炸药比能以及介质传递能量效率有关，可通过理论公式得到。

无模爆炸成形应用实例

内蒙古工业大学为某啤酒厂制造的5台直径4800mm双层金属球形清酒罐。该罐原设计为14mm厚柱形不锈钢结构，投资额120万元，后改为外壳为6mm厚16MnR，内衬为1.5mm厚1Cr18Ni9Ti。根据板料宽度设计为7节球内接锥台结构，爆炸成形装药量为1340gTNT炸药，成形后非球面度误差小于0.3%，实际工程费用仅为62万，降低成本近50%。球体爆炸成形前、后照片如图3、4所示。

图3 爆炸成形前壳体照片

图4 爆炸成形后球体照片

无模爆炸成形过程的有限元模拟

无模爆炸成形过程的有限元模拟采用了ANSYS 中LS-DYNA模块的三维壳体单元Thin Shell 163。该单元是4节点显性薄结构壳体单元，兼具弯曲挠度和薄膜分析功能，既可以施加平面载荷，也可以施加法向载荷，在每个节点上都有12个自由度，分别为X、Y、Z方向的位移、速度、加速度和沿X、Y、Z轴旋转的转角。在本模拟中是十分合适的单元类型。材料模型选取的是Plastic Kinematic Hardening，用自由划分法与其他划分方法相结合的方式来划分网格。为了便于观察，将整个壳体结构都作为分析模型，但是没有考虑焊缝区域，单元数量为11700个。其有限元模型如图5所示，经过1254次迭代完成计算过程。

图5 多节锥台壳体结构的有限元模型

变形结束后壳体的等效应力分布云图，如图6所示。从图中可以清晰地看出，变形结束后壳体的等效应力分布仍然是以中心纬度圈为对称轴上下对称的，呈环带状规律分布。而壳体的每一组成块也有同样的规律，即每块板料的中心部位应力最大，其他部位以中心部位为对称依次减小。由于在每块板料的中心部位相对于其他部分来说变形量最大，因此必然产生比较大的应力集中，是整个变形过程中减薄量最大的区域，因此也就是变形过程中的危险截面。

图6 等效应力分布云图

变形结束后壳体的等效应变分布图，如图7所示。从图中可以看出壳体变形结束后的等效应变分布规律与等效应力基本相同，这样就再次印证了在变形结束后，组成壳体的各个部分中，每个部分的中心位置都是变形量最大的区域，这些区域的壳体减薄量相对于其他区域来说要大得多，如果发生断裂等现象就必然从这些区域首先发生，因此这些区域就是应力集中的区域，就是整个壳体中最为危险的部分。而壳体的其他部分的等效应变仍是以中心部分为对称向上下两侧逐渐减小，呈现环带状分布，每个部分之间相互连接的位置变形量最小，基本与原壳体尺寸相等。

多节锥台壳体在第一象限中的平面简化图，如图8所示，θ角代表的是壳体上子午线的位置，P1、P2、P3是三个关键点。

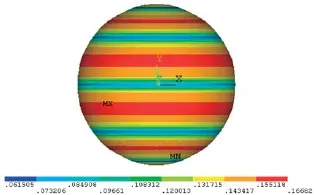
图7 等效应变分布图

图8 多节锥台壳体在第一象限中的平面简化图

为了准确表达球内接多节锥台壳体变形区域在爆炸冲击载荷下的成球精度，将成形球壳外表面距球心的距离减去多节锥台壳体外接球（成形目标球）半径的差值与多节锥台壳体外接球半径的比值定义为成球误差fr。

成形前后，成球误差fr沿子午线的分布规律，如图9所示。由图9我们可以很清楚的看出：变形以前，P1、P2、P3有相同的误差值-4.9%，但是随着变形的进行，整个壳体结构的成球误差都大大降低了。当变形过程结束以后，由数值模拟获得的球壳，在绝大部分的位置上的成球误差都小于±1%，但是上极板的中心位置的误差很大，大约为2.1%，这充分说明壳体平面部分的变形情况与壳体锥面部分的变形具有不同的特征，极板部位一维平面的变形抗力大大低于各锥台部位三维曲面的变形抗力，严重影响了薄壁多节锥台壳体爆炸胀球的精度，在工艺改进的时候要考虑增加上下极板变形抗力的方法，以提高球壳的成形精度。

通过球形容器无模爆炸成形过程的有限元分析，可以清楚的看到：球内接多节锥台壳体是球壳无模成形的理想壳体结构，它在高应变率下具有良好的趋球性能。ANSYS软件的LS-DYNA程序是一个高效的大变形分析程序，应用该程序来分析无模爆炸胀球过程，可对成形过程进行有效优化。

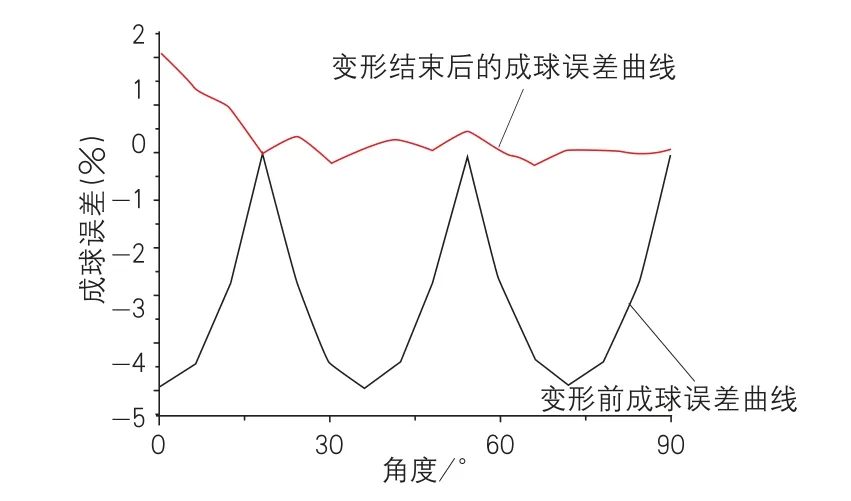
图9 成形结束后的成球误差分布

结束语

由于无模爆炸成形技术具有快捷、高效、低成本、不需要专用模具及成形设备、变更规格品种方便、封闭在壳体内炸药能量不会对环境产生污染等特点，已经广泛适用于各种尺寸的化工球形储罐的生产。无模爆炸成形技术已在工业球罐制造中取得重大成果，与此同时，也为常规方法难以加工的薄壁和超薄壁球壳的制造开创了一条新思路，所以该项技术具有一定的推广应用价值。