新型双转子发动机功率传输装置的运动学特性*

陈虎，徐海军，潘存云，邹腾安，江磊(.国防科技大学机电工程与自动化学院，湖南长沙40073；.中国北方车辆研究所，北京0007)

新型双转子发动机功率传输装置的运动学特性*

陈虎1，徐海军1，潘存云1，邹腾安1，江磊2
(1.国防科技大学机电工程与自动化学院，湖南长沙410073；2.中国北方车辆研究所，北京100072)

提出一种基于摆盘和凸轮组合机构的双转子发动机功率传输装置。其结构简单、布置方式完全对称，平衡性好，能够通过凸轮控制转子的运动规律。为分析和研究该机构的运行特性，通过欧拉法建立该机构的基本运动学模型，计算出其运行轨迹，凸轮轮廓线等。分析了主要结构参数，如滚子轴线夹角和摆盘倾角，对其容积变化规律的影响。主要结论如下:滚子轴线夹角越靠近90°，气缸容积变化幅值越大。摆盘倾角与容积变化规律是成正比的，对于四叶片活塞转子而言，摆盘倾角最大取值约为65°。在实际中，滚子轴线夹角最好取90°，摆盘倾角要在留出足够叶片活塞厚度的前提下尽量取较大的值。

双转子发动机；摆盘；凸轮；轨迹；滚子轴线夹角；摆盘倾角

时至今日，发动机已经过了一百多年的发展。在这期间，人们创造了各种形式的发动机，如往复活塞发动机、汪克尔三角转子发动机等，其中最成功也是应用最广的是传统往复式活塞发动机，虽然其技术成熟但也存在固有的缺点:功率密度低、配气机构复杂等［1］。汪克尔三角转子发动机虽然投入巨大但成效甚微，相比于往复式发动机，除了密封问题，还有由于狭小的容积腔导致燃烧不充分，复杂的加工和维修等问题有待解决［2-3］。然而随着能源危机，空气污染等问题的凸显，未来发动机要朝着轻型化、高功率密度和高效率的方向发展［4-5］。

基于上述原因，双转子发动机现已成为研究的热点，一系列新机型相继推出，如美国的MYT Engine［6］，俄罗斯的Yo-Mobile Engine等，大多数是基于行星齿轮机构。

本文研究的双转子活塞发动机功率传输装置在摆盘和凸轮组合机构［7］的驱动下，发动机在输出轴每转一周时，总共做功16次，因此可以在不显著改变发动机整体尺寸、重量以及制造成本的前提下，实现功率密度、升功率等大幅度的提升，这一特性有着广泛的应用前景。

本文主要对这种新型功率传输机构的运动特性进行分析，总结出一些重要参数对其性能的影响。

1 新型功率传输机构构成及工作原理

1.1 功率传输机构的构成

功率传输机构包括动力缸组件以及与动力缸组件相连的差速驱动组件，其中动力缸组件包括转子1、转子2及其上面固连的滑轨。如图1所示，转子1和2同轴且呈交错状安装于缸体内。如图2所示，差速驱动组件包括凸轮、动力轴、摆盘以及齿轮箱，它们组合形成自由度为1的驱动组件，凸轮为空心球壳，凸轮上开设有8字形外摆线槽，动力轴为中部一段为Z字斜轴。

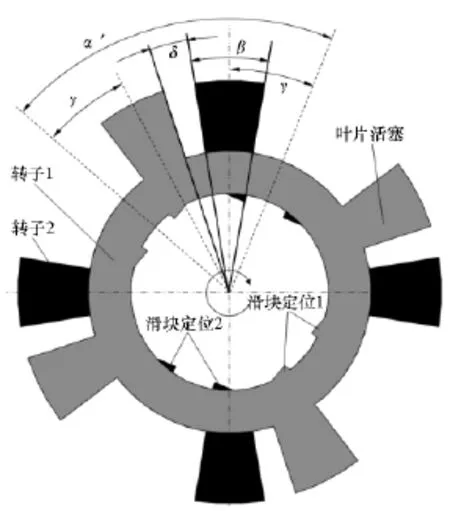
图1 动力缸组件示意图Fig.1 Diagram of power cylinder assembly

摆盘径向布有四个滚子，这些滚子分别与滑轨和凸轮配合运动，摆盘安设在Z字轴的斜轴段上并可绕其转动，摆盘径向相互垂直的四个方向向外伸出滚子轴，凸轮包裹在摆盘外并可绕动力轴旋转，凸轮上对称布置四个8字形外摆线槽，滚子轴上有两个滚子，靠近摆盘的滚子在8字形外摆线槽上沿凸轮面滚动，位于滚子轴末端的滚子在滑轨内沿直线滚动。驱动组件的输入端为摆盘上的滚子，输出端为Z字轴和凸轮轴。齿轮箱内装有等速反向器，即两个尺寸一致的大锥齿轮和两个尺寸一致的小锥齿轮。两个大的锥齿轮分别与Z字轴和凸轮轴固连。

1.2 工作原理

如图2所示，当发动机的输出轴(Z字轴3)匀速旋转一周时，Z字轴带动摆盘2绕轴心公转，齿轮箱驱动凸轮4与Z字轴做反向同步转动，凸轮通过其上面的凸轮槽内滚动的滚子轴5约束摆盘绕中心斜轴自转，方向与其公转方向相反。在摆盘旋转过程中，滚子轴5a和5b间的夹角在输出轴端面的投影呈周期性变化。在输出轴转过一周的过程中，摆盘相对于输出轴(Z字轴)的斜轴段反向自转两周，而滚子轴间夹角输出轴端面的投影周期变化四次，相当于滑轨1a和滑轨1b的夹角变化四次，也是两个转子间的夹角周期变化四次，每个转子上有四个叶片活塞，每两个活塞形成一个容积腔，共有八个这样的容积腔。输出轴转动一周，每个容积腔周期变化四次，所以一共变化32次，相当于做功16次，大大提高发动机功率密度。每一瞬间都同时有2工作腔处于做功冲程，理论上工作更为平稳，从而有效地降低各机械零件的磨损，并延长发动机的使用寿命。由于在齿轮箱的驱动下凸轮和Z字轴反向同步转动，所以也可以将凸轮作为另一个输出端进行对转输出，可应用于当下热门的对转浆飞机、舰船和便携式飞行器等。

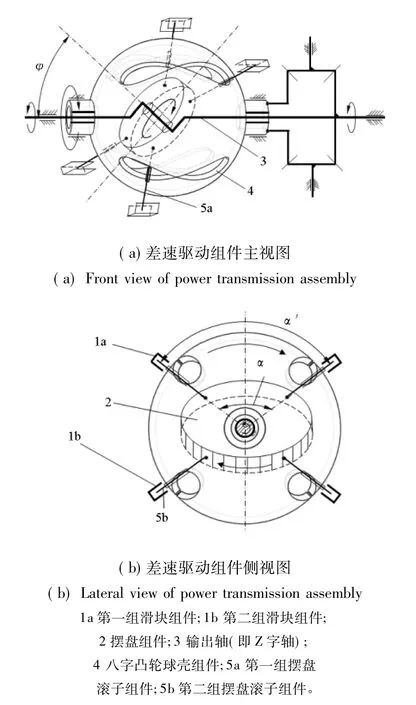
图2 差速驱动组件结构示意图Fig.2 Structure diagram of differential driving assembly

2 关键部件运动学建模与分析

2.1 坐标系及相关符号定义

为了描述和确定各构件的位置和姿态，设两转子顺时针旋转，建立坐标系。

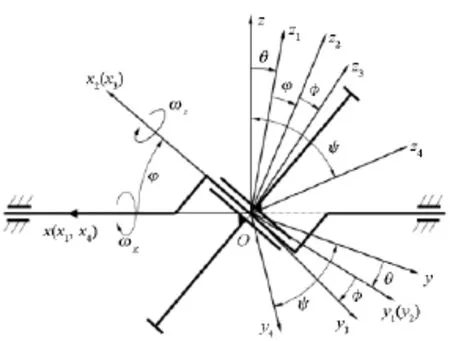
图3 坐标变换及参数示意图Fig.3 Coordinate transformation and parameters

定义相关参数如下:

①转子部件主要结构参数:两转子上相邻叶片活塞的夹角用δ表示；压缩比(即δmax/δmin)用ε表示；转子上叶片活塞的宽度角用β表示；转子1和转子2上叶片活塞中心线与相邻最近的滑块定位中心线夹角分别用γ表示(或90°-γ)；两转子上相邻滑块定位中心线的夹角用α'表示。

②功率传输机构主要结构参数:摆盘倾角(即Z字轴倾斜角)用φ表示；输出轴的转动角位移用θ表示；摆盘绕其中心的自转角位移用φ表示；两组摆盘滚子组件中心线在摆盘转动平面的夹角用α表示；8字凸轮球壳组件的转动角位移用ψ表示。

③主要坐标参数:设摆盘中心线与输出轴中心线相交于点O，如图3所示以点O为坐标原点，过原点以输出轴旋转负方向(在图3中设输出轴顺时针旋转为正方向)为x轴正方向，在过原点且垂直于x轴的平面上以原点为起点做两条互相垂直的射线，分别为y轴和z轴，坐标系xyz为固定坐标系。将坐标系xyz过原点绕x轴顺时针旋转角度θ，得到坐标系x1y1z1，其x1轴与x轴重合，y1轴与y轴、z1轴与z轴的夹角均为θ，坐标系x1y1z1为输出轴本体坐标系，也为摆盘公转坐标系。同样地，将坐标系x1y1z1过原点绕y1轴顺时针旋转角度φ，得到坐标系x2y2z2，其y2轴与y1轴重合，x2轴与x1轴、z2轴与z1轴的夹角均为φ，坐标系x2y2z2为摆盘转动平面坐标系。最后，将坐标系x2y2z2过原点绕x2轴顺时针旋转角度φ，得到坐标系x3y3z3，其x3轴与x2轴重合，y3轴与y2轴、z3轴与z2轴的夹角均为φ，坐标系x3y3z3为摆盘本体坐标系。为了描述凸轮球壳的运动及凸轮型线也需要建立一个坐标系。将坐标系xyz过原点绕x轴顺时针旋转角度ψ，得到坐标系x4y4z4，其x4轴与x轴重合，y4轴与y轴、z4轴与z轴的夹角均为ψ，坐标系x4y4z4即为凸轮球壳本体坐标系。

2.2 运动学模型建立

要建立机构的运动学模型首先要知道各部件的运动关系，2.1节已经建立了各部件的坐标系，现在需要建立各个坐标系之间的联系，即求出惯性坐标系与本体坐标系之间的变换矩阵。

从一个坐标系到另一个坐标系的变换可以用如下形式的矩阵表示［8］

其中，x为惯性坐标系中的矢量，x'为本体坐标系中的矢量。A为旋转矩阵，也为变换矩阵，其完全描述了这两个坐标系的变换关系，它包含三个独立参数。

如图3所示，想要知道摆盘上的点在固定坐标系xyz上的坐标轨迹需要做三次坐标变换，首先，已知摆盘上的点在摆盘本体坐标系x3y3z3中的位置坐标，将其转换到摆盘转动平面坐标系x2y2z2中，相对而言，摆盘转动平面坐标系x2y2z2为惯性坐标系，而摆盘本体坐标系x3y3z3为本体坐标系。这两个坐标系之间的关系是坐标系x2y2z2过原点绕x2轴顺时针旋转角度φ得到坐标系x3y3z3，即摆盘本体坐标系x3y3z3绕x3轴逆时针旋转角度φ得到坐标系x2y2z2。此次转动发生在y3z3平面，故得到其变换矩阵为

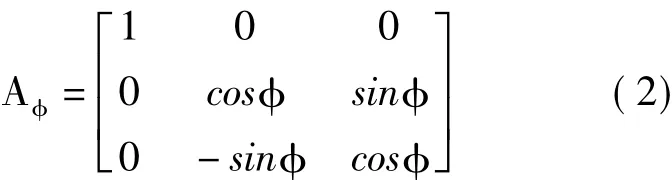
同理可得，将摆盘上的点在摆盘转动平面坐标系x2y2z2中的位置坐标转换到输出轴本体坐标系x1y1z1的变换矩阵为

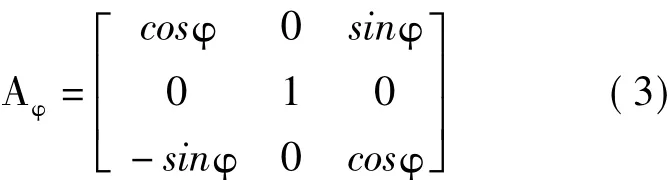
将摆盘上的点在输出轴本体坐标系x1y1z1中的位置坐标转换到固定坐标系xyz的变换矩阵为

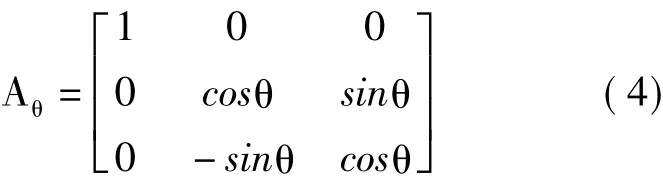
于是从摆盘本体坐标系x3y3z3到固定坐标系xyz的总变换矩阵为

由式(1)可得出其逆变换，即由惯性坐标系向本体坐标系的转换，可表示为

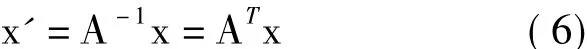
变换矩阵为正交矩阵［8］，其逆矩阵等于其转置矩阵。

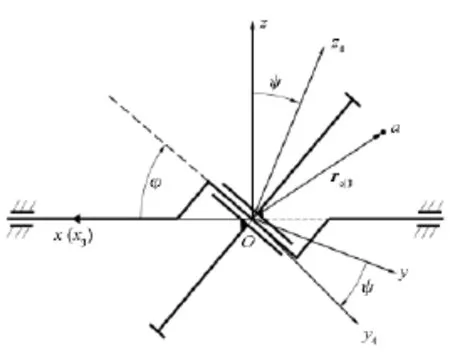
图4 八字摆线轨迹向量图Fig.4 8 shape cycloid vector

2.2.1 运动轨迹计算

基于上述坐标变换，现在可以计算摆盘上点的轨迹。如图4所示，设在摆盘上有一个点a，其在坐标系x3y3z3上的方向向量可表示为ra3，其在坐标系xyz上的方向向量可表示为ra0，则根据式(5)，摆盘上的点的轨迹可用式(7)表示

为了让方程更加简化，可以在摆盘本体坐标系上取点a的方向向量ra3=［0 0 r］T，由于摆盘上各点的轨迹形状一致只是相位不同，所以一个向量可以展现出其轨迹的性质，故将ra3代入式(7)可以得出轨迹矩阵为

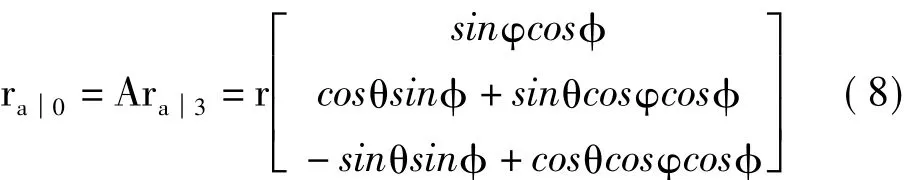
根据上述坐标变换过程，凸轮球壳本体坐标系x4y4z4为本体坐标系，固定坐标系xyz为惯性坐标系，这两个坐标系之间的关系是将坐标系xyz过原点绕x轴顺时针旋转角度ψ得到坐标系x4y4z4。即凸轮球壳本体坐标系x4y4z4绕x4轴逆时针旋转角度ψ得到坐标系xyz。此次转动发生在y4z4平面，故得到其变换矩阵为

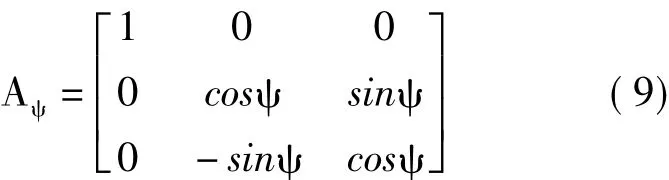
要将摆盘上的点在固定坐标系xyz中的位置坐标转换到凸轮球壳本体坐标系x4y4z4中，根据变换矩阵的性质得到其变换矩阵=。

根据式(7)和式(9)将摆盘上点a的轨迹转换到凸轮球壳坐标系上，即可求出凸轮球壳上8字外摆线的方程，则

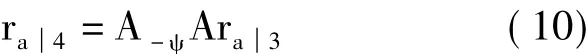
该轨迹即为与摆盘等速旋转时的8字外摆线中心轮廓型线方程。同理，为了让方程更加简化也可以取方向向量ra3=［0 0 r］T，则根据式(8)可得

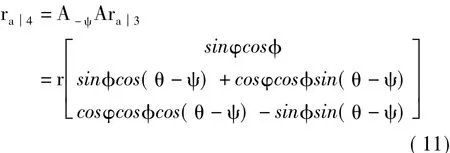
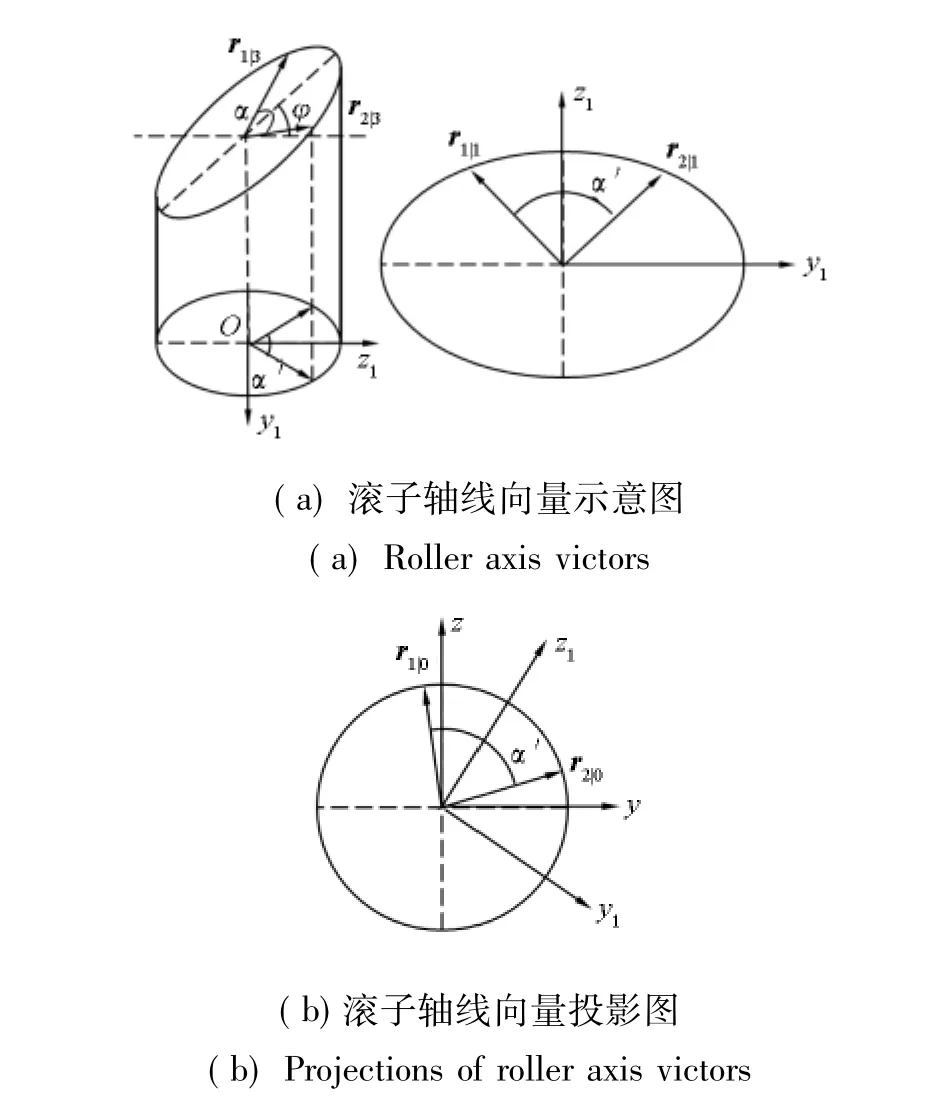
图5 滚子轴线夹角投影示意图Fig.5 Projection of roller axis angle

2.2.2 夹角关系计算

对于发动机而言，气缸的容积变化规律是极其重要的参数，能够体现各个冲程的交替规律、活塞运动和热力循环等。对于本方案发动机，转子上叶片活塞间的夹角变化规律就能够决定容积变化。如图5所示，根据所设计的链接关系，转子组件上的滑块定位槽1和滑块定位槽2分别与功率传输机构的第一组滑块组件和第二组滑块组件配合相连，使它们在周向同步转动，所以两个滑块组件在转子周向的夹角变化就决定了两转子上叶片活塞之间的夹角关系，而根据第二节的运动设计，两个滑块组件的夹角是由摆盘上成一定角度的两个滚轴在转子转动平面的投影形成的。故摆盘上两个滚轴的夹角和摆盘与输出轴所成的角度是决定转子夹角变化，即气缸容积变化规律的关键。

如图5所示，摆盘上滚子组件端点在摆盘转动平面坐标系x2y2z2上的运动轨迹是一个在y2z2平面上以摆盘自转中心，即原点为圆心，滚轴端点到中心距离为半径的圆。由于存在摆盘倾角φ，这个圆形轨迹投影到固定坐标系x1y1z1上为一个在y1z1平面椭圆轨迹，如果想要得到其跟滑块组件的夹角运动关系还要将其投影到固定坐标系上。由于此计算与长度无关，只涉及角度，为减少不必要的参数不妨设摆盘上相邻的两个滚轴在摆盘本坐标系x3y3z3上向量的单位向量分别为r13=和=并且对称于z3轴两侧，其转换到摆盘转动平面坐标系x1y1z1上的向量为r11=ΑφΑφr13和r21= ΑφΑφr23，转换到固定坐标系xyz上的向量为r10=Αr13和r20=Αr23。如图5(a)所示，r13与r23之间的夹角为α，而其又为单位向量，则相应地，这两个向量可以表示为

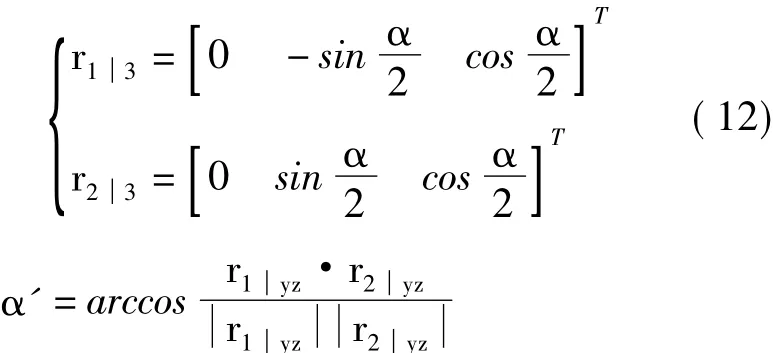
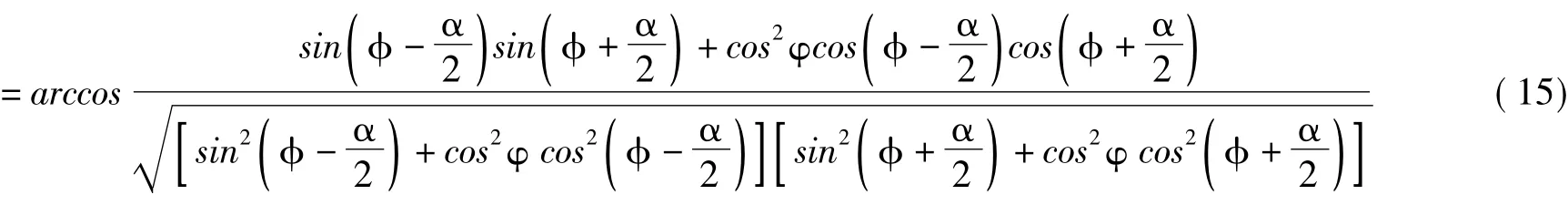
根据转换关系，则向量r13与r23投影到坐标系xyz上的向量为

如图5(b)所示，滑块组件绕x轴转动，即相邻两组滑块组件的夹角在yz平面内变化，r11与r21之间的夹角和r10与r20之间的夹角在平面yz上的投影即为相邻滑块组件夹角，用α'表示。因此在二维平面yz上产生了两个平面向量r1yz与r2yz，分别为第一组滑块组件和第二组滑块组件的方向向量。根据上述分析，这两个向量可表示为

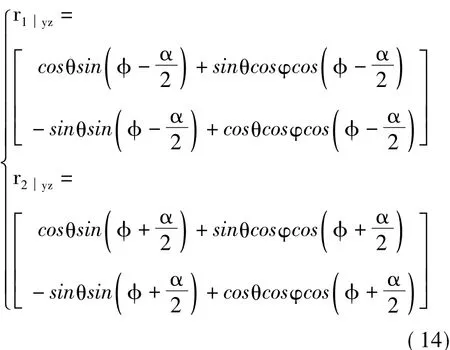
所以，第一组和第二组滑块组件的夹角可以表示为［9］

如图6所示，在圆上r13和r23之间的夹角α不变，所以r13和r23在圆上所围成的扇形面积S不变，又因为r13和r23所在坐标平面y3z3与y1z1或yz的夹角始终为φ，由面积射影定理可知，r11与r21之间的夹角(即r10与r20之间的夹角)在平面yz上的投影面积S'也始终不变［9］，且其值恒为S·cosφ。因此在二维平面yz上产生了两个平面向量r1yz和r2yz与椭圆围成的扇形面积在φ变化过程中始终等于S·cosφ。所以问题转换为在椭圆中过中心的一个角，其角平分线由短轴向长轴转动且保持其与椭圆所围成的扇形面积不变的情况下，其大小的变化情况。

如图6所示，对于椭圆中一个值固定的角，当其对角线由l顺时针转动一个微小的角度Δφ至l'时，设其与椭圆所围面积的面积增量为ΔS，其值等于ΔS1-ΔS2，其中ΔS1为向量r11一边减小的面积增量，ΔS2为向量r21一边增加的面积增量。

当Δφ非常小时，ΔS1和ΔS2近似为扇形，所以由扇形面积公式可得

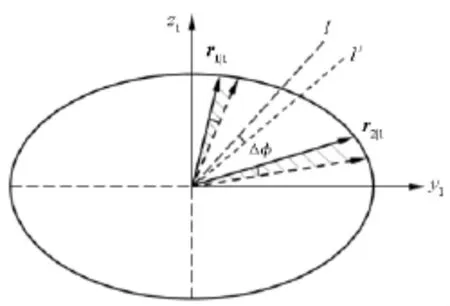
图6 滚子中心线夹角投影面积增量示意图Fig.6 Incremental area of projection of roller axis angle

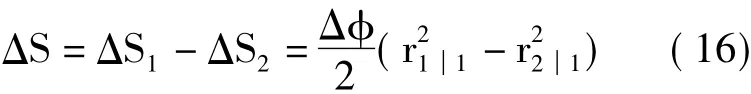
所以，要使角与椭圆所围面积恒定不变，则必须使中心角减小。

故滑块夹角的最大值和最小值分别为

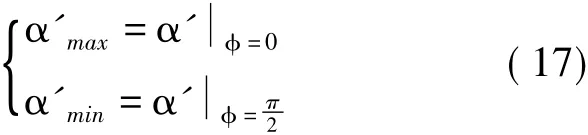
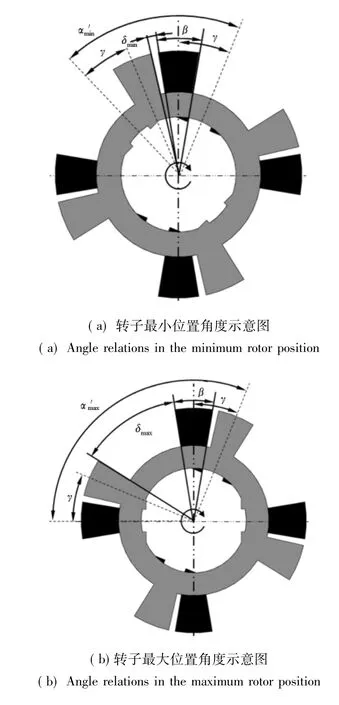
图7 转子角度参数关系示意图Fig.7 Relationship of angle parameters in rotor

如图7所示，根据几何关系，由于本文讨论的是每个转子上有两个滑轨和四个叶片活塞的情况，所以可以得出，当其中两个滑轨之间夹角为时，相邻两滑轨之间的夹角就是对应的= 90°-，同理，两个叶片活塞之间的夹角(δ1和δ2)和叶片活塞厚度的关系，则

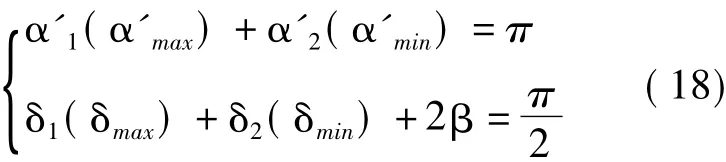
根据角度之间的关系可以得出

4 仿真计算与分析

根据上述对转子运动部件的建模，在MATLAB［10］中进行编程，得出各参数的特性曲线并分析相关的量对曲线的影响。

4.1 初始参数

计算用主要参数如表1所示。

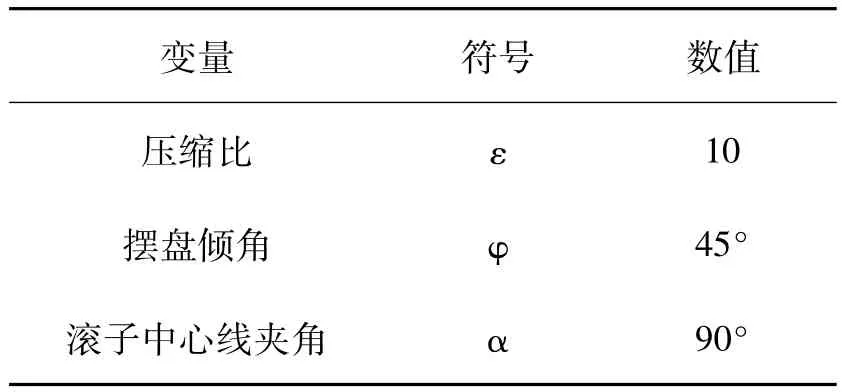
表1 仿真的初始参数Tab.1 Simulation initial parameters

4.2 模拟结果

4.2.1 摆盘上点的位移轨迹

如图8所示，摆盘上的点(即为滚子运动轨迹)为一种平滑对称的空间曲线。图(a)为曲线的空间三维图，其他三幅图分别是该曲线在xy，xz和yz平面的投影视图。从曲线中可以看出，滚子在摆盘公转和自转的过程中一周达到四次极限位置，这也与滑块间夹角在主轴每转一周过程中的变化周期一致。

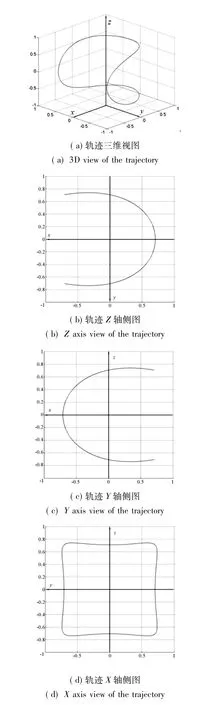
图8 滚子运动轨迹示意图Fig.8 Roller trajectory

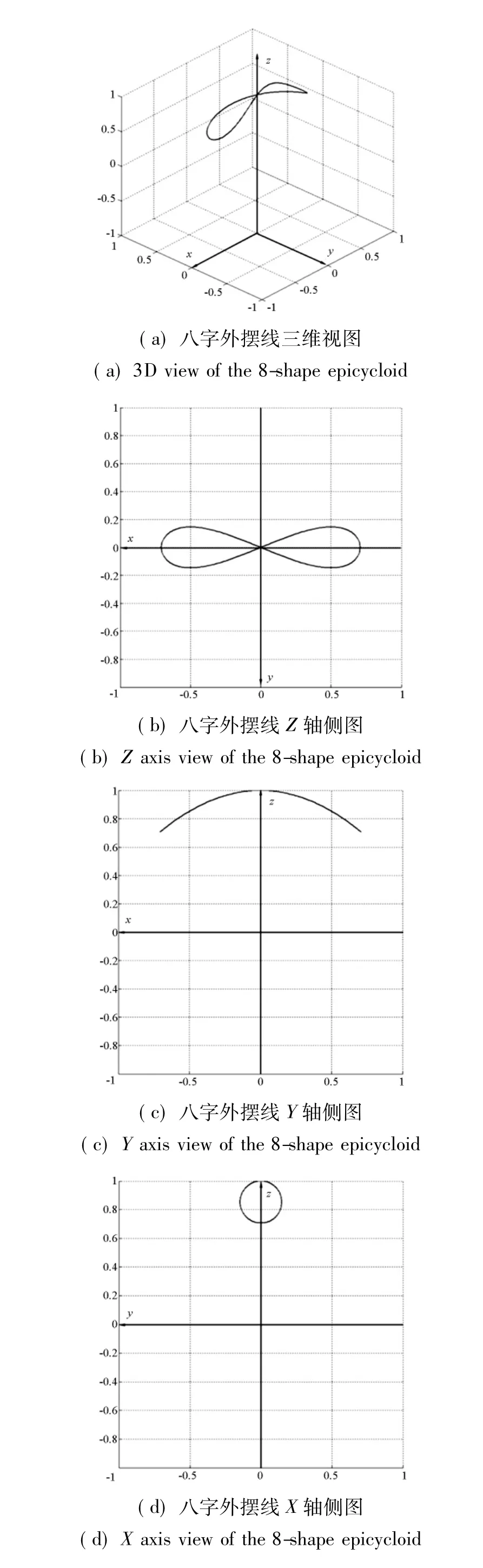
图9 八字摆线轮廓线示意图Fig.9 8 shape cycloid profile

4.2.2 八字外摆线凸轮中心线轨迹

凸轮球壳上8字凸轮轨迹中心线如图9所示。图9(a)为曲线的空间三维图，其他三幅图分别是该曲线在xy，xz和yz平面的投影视图。滚子不仅受到摆盘的约束，同时也受到凸轮的限制，这两个约束使得滚子能够实现图8所示的运动。凸轮球壳的等速对转也限制了摆盘自转的自由度，使得本来有两个自由度的摆盘机构以唯一的轨迹运动。通过跟图8的对比可以看出，滚子在主轴旋转一周过程中达到四次极限位置，而凸轮只有两个极限位置，这就说明滚子每转一周要在凸轮上运动两个来回。

4.2.3 相邻叶片活塞夹角变化曲线

相邻两个叶片活塞分别属于不同的转子，它们之间的变化就是气缸容积变化。如图10所示，在主轴旋转一周过程中，容积变化四次(往复式活塞是0.5次［11］)，与滚子周期一致，大大提高了单缸频率，这对提高功率密度是非常有利的。其变化曲线比较平滑，与往复式活塞发动机类似都是类正弦曲线，在给定的结构条件下，其变化幅值能够达到39°。

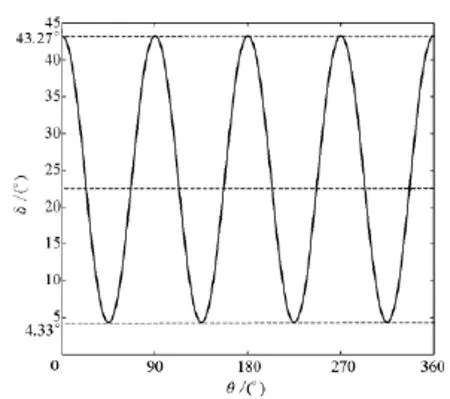
图10 相邻叶片活塞夹角变化规律示意图Fig.10 Angle variation diagram of adjacent blade piston

4.2.4 关键结构参数的影响

图11所示为在不同值的滚子轴线夹角α下气缸容积变化(即相邻叶片活塞夹角变化)曲线。如图11所示，在摆盘倾角φ不变时，随着夹角α的增大，容积变化幅值先增大再减小，在α=π/2达到最大值。

虽然α从0到π/2过程中对应的曲线组(组A)与α从π/2到π过程中对应的曲线(组B)幅值、周期和变化趋势均一致，但是它们除了极值点外，并没有重合。其实它们是一一对应的，因为摆盘是一个整圆，四个转子两两成一条直线，两两滚子中心线夹角互为补角，所以除了α=π/2外，其他值所对应的曲线会导致相邻两次容积变化规律不同，而且越偏离α=π/2越明显，所以α最好取π/2。

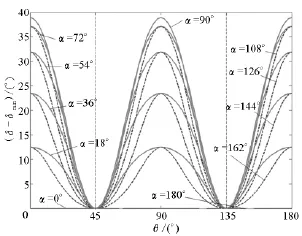
图11 滚子轴线夹角对容积变化的影响示意图Fig.11 Effect of roller axisangle to volume variation

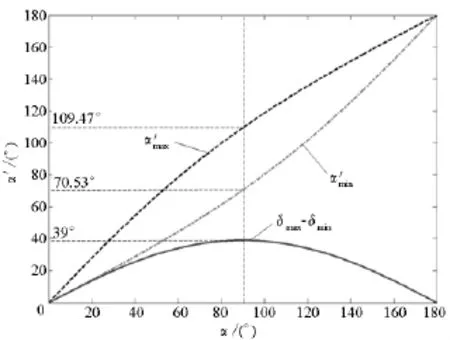
图12 α'max和α'min与α的关系曲线Fig.12 Relationship amongα'max，α'minandα

图12 所示为滑块组件定位中心线夹角最值α'max和α'min与滚子轴线夹角α的关系曲线。α'max和α'min均与α成正比关系。此曲线也同时证明了图11所得出的结论。

图13所示为摆盘倾角φ与容积变化规律的关系。随着摆盘倾角φ的增大，α'max逐渐增大，而α'min逐渐减小，而且这个趋势是越来越快的。当然，它们的差值(即容积变化规律)也是增大的。由于本文所研究的是四叶片转子，所以根据式(20)，α'max≤135°，α'min≥45°，所对应的摆盘倾角φ约为65°。所以在选择φ时不能超过65°，才能保证叶片不受干涉，并且为保证叶片活塞有一定厚度(强度)，摆盘倾角φ要远离65°。因此，在实际中既要尽量取较大的摆盘倾角来增大容积变化幅值，提高燃烧效率［11］，又要留出叶片活塞的足够厚度来保证其强度。

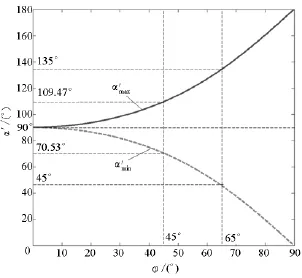
图13 φ与容积变化规律的关系示意图Fig.13 Relationship betweenφand volume variation

5 结论

1)本文提出了一种基于摆盘和凸轮组合机构的双转子发动机功率传输装置。其结构简单、平衡性好；凸轮曲线变化多样，可以适应不同的转子运动规律。

2)在该机构的驱动下，转子容积变化规律为主轴每转一周容积变化四次，在理论上大幅提高了功率密度。

3)滑块组件定位中心线夹角最值α'max和α'min均与α成正比关系。滚子轴线夹角α越靠近π/2，气缸容积变化幅值越大。在除了α=π/2外的其他取值会造成相邻两次容积变化规律不同，而且越偏离α=π/2越明显，所以α最好取π/2。

4)摆盘倾角φ与容积变化规律是成正比的。对于四叶片活塞转子而言，摆盘倾角φ最大取值约为65°。在实际中选取摆盘倾角φ既要尽量取较大的值来增大容积变化幅值，提高燃烧效率，又要留出叶片活塞的足够厚度来保证其强度。

References)

［1］Yamamoto K.Rotory engine［M］.Japan:Sankaido Co.，Ltd:1981.

［2］练永庆，王树宗，马世杰.斜盘式气动发动机动力学仿真［J］.机械工程学报，2008，44(1):243-246.LIAN Yongqing，WANG Shuzong，MA Shijie.Dynamics simulation of swash-plate pneumatic engine［J］Mechanical Engineering，2008，44(1):243-246.(in Chinese)

［3］Heywood JB.Internal combustion engine fundamentals［M］.Singapore:McGraw-Hill，1988.

［4］Chen H，Pan C Y，Xu H J，et al.Analysis on structural characteristics of rotors in a twin-rotor cylinder-embedded piston engine［J］.Journal of Central South University，2014，21(6):2240-2252.

［5］Morgado R G.Internal combustion engine and method.US［P］.20070199537A1，2007-08-30.

［6］Yarovit Yo-Mobile［EB/OL］.［2012-10-12］.https://en.wikipedia.org/wiki/Yo-Mobile.

［7］陈虎，潘存云，徐小军，等.一种摆线凸轮与摆盘机构组合的功率传输装置.中国专利［P］.201410496050.3，2014-09-25.CHEN Hu，PAN Cunyun，XU Xiaojun.An power transmission apparatus combined by cycloid-cam and swing plate.China［P］.201410496050.3，2014-09-25.(in Chinese)

［8］叶其孝，沈永欢.实用数学手册［M］.2版.北京:科学出版社，2006.YEQixiao，SHEN Yonghuan.Practicalmathematics handbook［M］.2nd ed.Beijing:Science Press，2006.(in Chinese)

［9］秦敢，向守平.力学与理论力学(下册)［M］.北京:科学出版社，2014.QIN Gan，XIANG Shouping.Mechanics and theoretical mechanics(lower volume)［M］.Beijing:Science Press，2014.(in Chinese)

［10］王正林，刘明，陈连贵.精通MATLAB 7［M］.北京:电子工业出版社，2006.WANG Zhenglin，LIU Ming，CHEN Liangui.Master MATLAB 7［M］.Beijing:Publishing House of Electronics Industry，2006.(in Chinese)

［11］周龙保.内燃机学［M］.2版.北京:机械工业出版社，2009.ZHOU Longbao.Internal combustion engine［M］.2nd ed.Beijing:Mechanical Industry Press，2009.(in Chinese)

Kinematic performance of new-type power transm ission mechanism in tw in-rotor piston engine

CHEN Hu1，XU Haijun1，PAN Cunyun1，ZOU tengan1，JIANG Lei2
(1.College of Mechatronics Engineering and Automation，National University of Defense Technology，Changsha 410073，China；2.China North Vehicle Research Institute，Beijing 100072，China)

A power transmission mechanism of twin-rotor engine based on wobble plate and cam was proposed.The advantages of the power transmissionmechanism of twin-rotor engine based on wobble plate and cam are simple structure，completely symmetrical arranged，good balance，and themovement is controllable.For analyzing its operating characteristics，the basic kinematicmodelwas established by Euler-equation，and its trajectory and cam contour lines were obtained.Effects on volume variation of themain structural parameters，such as plate inclination angle and roller axis angle were analyzed.Main results are as follows:the closer to 90°roller axis angle is，the larger volume variation is.Plate inclination angle is proportional to volume variation.For 4-blade pistons rotor，themaximum plate inclination angle is approximately 65°.In practice，the best roller axis angle is 90°，plate inclination angle should be large enough after taking the thickness of blade piston into account.

twin-rotor engine；wobble plate；cam；trajectory；plate inclination angle；roller axis angle

TK401

A

1001-2486(2015)05-075-09

10.11887/j.cn.201505012

http://journal.nudt.edu.cn

2015-03-25

国家自然科学基金资助项目(51475464)

陈虎(1986—)，男，辽宁阜新人，博士研究生，E-mail:chenhu19861124@163.com；徐海军(通信作者)，男，讲师，博士，E-mail:xuhaijun_1999@163.com