基于RVM算法的蓄电池SOC预测

侯江娜，孙玉坤，王鹏飞

(江苏大学电气信息工程学院，江苏镇江212013)

基于RVM算法的蓄电池SOC预测

侯江娜，孙玉坤，王鹏飞

(江苏大学电气信息工程学院，江苏镇江212013)

由于蓄电池真实的荷电状态与多种因素如电池温度、充放电电压、充放电电流和电池老化等成高度非线性，使得蓄电池荷电状态预测模型建立困难，且预测精度差。针对以上问题，用基于相关向量机的预测方法，以电池充电端电压和充电电流为输入量、电池的荷电状态为输出量建立预测模型，分析该模型性能与高斯核函数带宽之间的关系。通过分析得出，高斯核函数带宽取值为0.9时，相关向量机方法具有较为理想的预测效果。与支持向量机模型相比较，该模型稀疏性强、复杂度低、预测时间短，并提高了对新测试样本点的预测精度，泛化能力强。

电池荷电状态；相关向量机；高斯核函数；稀疏性；泛化能力

蓄电池储能具有容量大、寿命长、污染小及低维护等优点，广泛用于电动汽车、航空航天及通信电源等领域。蓄电池的荷电状态(State of Charge，SOC)表征了蓄电池的运行状态，准确的SOC检测可以为蓄电池的及时充电和维护提供信息，是蓄电池能量管理系统的重要组成部分。蓄电池SOC值无法直接测量，一般通过检测蓄电池的外部特性——蓄电池充放电电压、充放电电流、充放电温度和电池老化程度等参数，运用数学运算推断得到。蓄电池的充放电过程是一个复杂的化学反应过程，这些参数的内部关系会随着蓄电池运行状态的改变而改变，给蓄电池SOC建模增加了困难，使得蓄电池SOC建模成为该储能领域的热点和难点之一。

目前估算蓄电池SOC的建模方法主要有以经典数学模型为基础的传统方法、神经网络法和支持向量机法。传统数学模型方法需要大量的经验参数和假设条件，相应的模型复杂，难以求解，预测精度低，泛化能力差。神经网络方法训练时间长、收敛速度慢，且容易陷入局部最优的误区。支持向量机方法有效克服了神经网络的缺点，但支持向量的个数会着随着训练样本的增大成线性增长，稀疏性差，使得预测模型相对复杂，不适合大样本训练，且只能给出输出值，无法给出预测值的统计信息。

Tipping于2001年在贝叶斯框架基础上提出了一种数据分类与回归新方法——相关向量机(Relevance Vector Machine, RVM)法，它与SVM具有类似的函数形式，均是基于核函数映射将低维空间非线性问题转化为高维空间的线性问题，但是，RVM的训练以贝叶斯框架为基础，在先验参数结构下基于主动相关决策理论移除不相关点而建立稀疏化模型[1]，在样本数据迭代训练过程中，大部分后验分布权值趋于零，而非零权值所对应的学习样本，即相关向量，体现了数据样本的最核心特征。

文献[2]运用相关向量机方法对蓄电池荷电状态进行预测，但没有给出模型性能与核函数宽度之间的关系，无法准确得出最优RVM预测模型。本文以电池充电端电压和充电电流为输入量，以电池的荷电状态为输出量，运用RVM方法建立蓄电池荷电状态预测模型[3]，同时分析了模型性能与核函数宽度之间的关系，确定了最优预测模型。与传统数学模型方法、ANN方法、SVM方法相比，该方法无需大量的经验参数和假设条件，其模型输出为概率输出，具有很好的统计特性。该方法与文献[2]方法相比，可以寻优得到最佳核函数宽度，预测效果更好。数据仿真表明，该方法所建立的SOC模型预测精度高、泛化能力强，同时模型的稀疏性更好，预测时间更短。

1 相关向量机建模

1.1 模型描述

RVM模型是一种非线性概率模型，其预测模型为：

式中：为观测向量；(,)为核函数；棕=(棕0,棕1,…,棕)为权重。

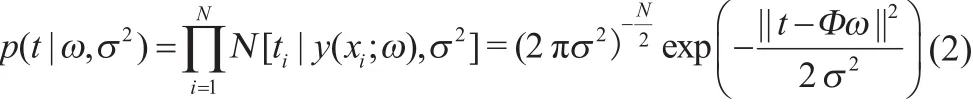
定义预测模型后，如果直接使用最大化似然函数(Maximum Likelihood)的方法求解和，结果通常是因使用过多的支持向量而导致过拟合。为此可以在贝叶斯框架下用最大似然估计来训练模型权值，为了控制预测模型的复杂性和避免过拟合，贝叶斯方法为每个权值定义了均值为0，方差为的高斯先验条件概率分布：

1.2 模型参数推断

t的概率分布式(2)和权值的先验条件概率分布式(3)都是高斯函数的乘积，可以对它们进行定积分运算，因此根据公式(2)和公式(3)，由贝叶斯定理推导得出权值w的后验概率分布为：

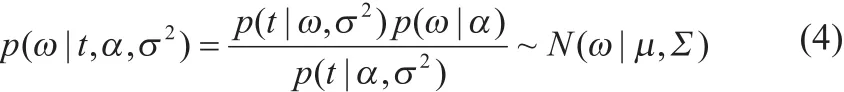
其中后协方差和均值分别为：

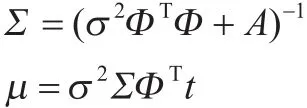
为了估计模型权值，首先要估计超参数的最佳取值。通过对权值变量进行积分并对其实现边缘化，RVM模型中的参数关系如图1所示，从而求得超参数的边缘似然分布为：

图1 RVM模型中的参数关系

RVM模型权值的估计值由后验分布的均值给出，它也是权值的最大后验分布，权值的最大后验估计取决于超参数和。假定最大似然参数估计值为和，超参数和方差可由公式(5)取最大值得到，将公式(5)对和偏微分后等于零得到：

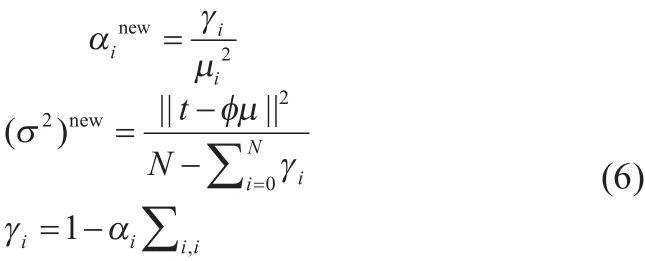
1.3 回归预测

式中：

2 蓄电池荷电状态预测模型

2.1 实验方法

蓄电池的荷电状态受电池充放电电压、充放电电流、温度及电池老化程度等因素的影响而发生变化。本实验以循环寿命为89.7%、10的钛酸锂电池为例，在(25±2)℃恒温情况下对蓄电池进行循环恒流充电、恒压充电、搁置、恒流放电、搁置、恒流充电。

在温度和老化程度一定的情况下，选择电池恒流充电过程中的端电压U(mV)、电流I(mA)为输入量，即=X(U,I)，电池的SOC为输出量，建立RVM模型。本实验在经过多次恒流充电、恒压充电、搁置、恒流放电、搁置后对恒流充电过程中的数据进行采集。其中一部分数据作为训练集进行模型训练，根据拟合精度和所需支持向量数分别分析模型的拟合能力和稀疏性；另一部分数据作为模型测试集，根据其预测精度分析模型的主要功能即泛化能力。蓄电池循环充放电的一个完整过程中，电池电压随着充放电时间变化而变化的过程如图2所示，其中恒流充电阶段分为2个部分：第一部分为平台电压部分，占恒流充电过程的80%～90%，且基本成线性；第二部分呈电压急剧上升趋势，处于恒流充电过程的最后阶段。

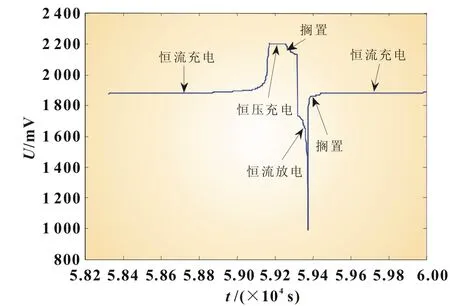
图2 蓄电池充放电特性曲线

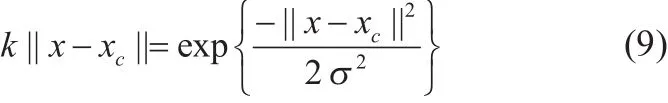
2.2 数据预处理

由于输入变量的范围差别较大，为了便于数据的处理，加快算法的收敛速度，首先对数据集进行归一化处理。本文将原始数据映射到[－1,1]内，其归一化函数式为：

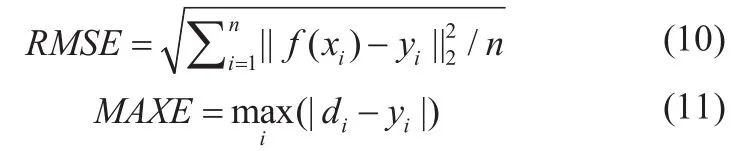
2.3 核函数及相关参数优化

首先RVM要选择适当的核函数，将特征向量映射到高维空间。常用的核函数有线性核函数、多项式核函数、径向基核函数、Sigmoid核函数和复合核函数等。其中径向基核函数中的高斯核函数具有较强非线性、可分性和局部性的优点，本文选择高斯核函数作为核函数：

式中：为核函数中心；σ为核函数的带宽，控制函数的径向作用范围。

选择高斯核函数最重要的是核函数带宽参数σ的选择，带宽过小会导致过学习，带宽过大则导致过平滑，都会引起回归能力的下降，它与RVM模型性能(稀疏性、拟合能力、泛化能力)存在复杂的关系，很难用数学运算推理。粗略取带宽参数σ的可行区间为[0,1]，在0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9共9个点上研究RVM模型性能与带宽之间的关系。本文采用均方根误差(RMSE)和最大误差(MAXE)定量评估RVM模型的拟合能力和泛化能力。均方根误差和最大误差的函数为：

表1反映了核函数宽度选择与RVM模型性能之间的关系。可以看出σ较小时，模型稀疏性差，使得模型相对复杂，过强的学习能力导致泛化能力下降，说明了带宽选择过小会导致过学习现象。σ取0.5、0.6、0.7、0.8、0.9时，模型的拟合能力和泛化能力逐渐增强，由于本文主要利用RVM模型完成对蓄电池SOC值的预测功能，因此分析可得：核函数宽度σ=0.9时效果最佳，模型相对简单，使得预测时间短且泛化能力强。

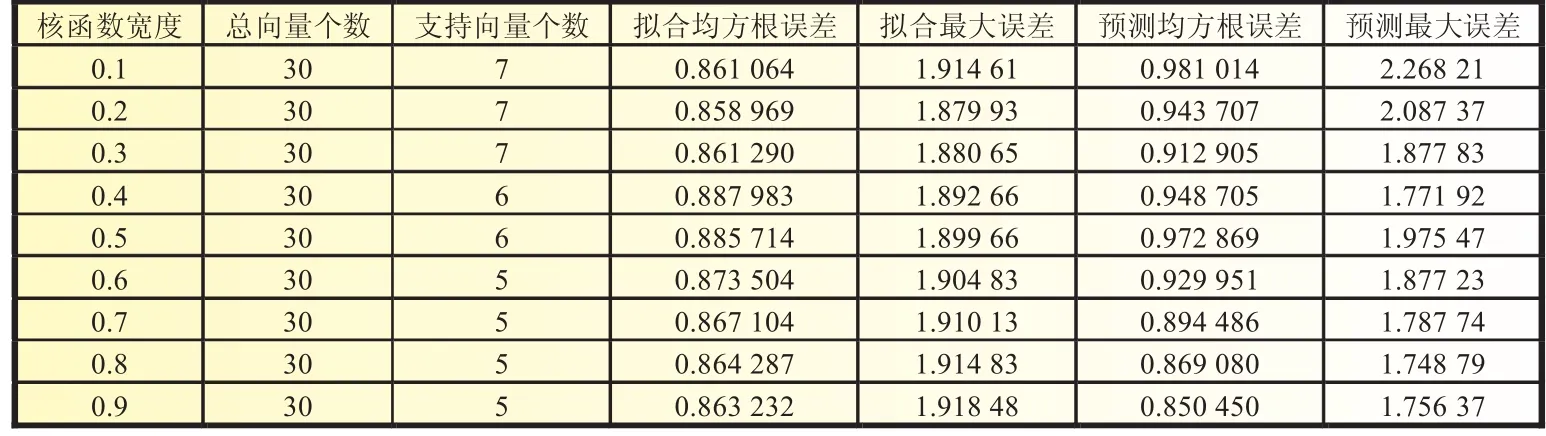
表1 核函数宽度与模型性能的关系

2.4 建模和预测

RVM模型的建立和新样本推测过程如图3所示。

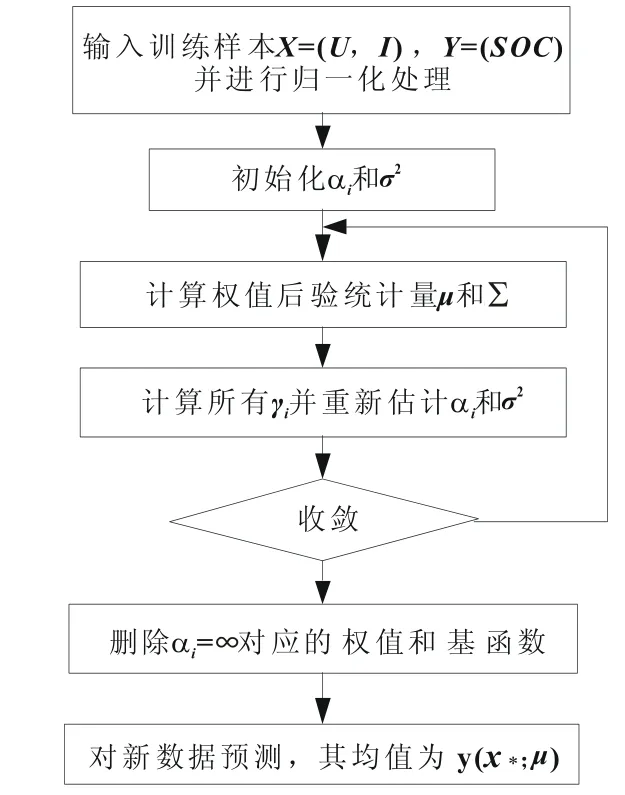
图3 RVM模型预测推理流程

(1)由公式(8)完成对输入样本的归一化处理；

(2)对α和σ2进行初始化处理；

(3)通过公式(4)计算后协方差和均值μ；

(4)利用公式(6)对初始化后的α和σ2不断进行迭代更新直至找到最优参数αMP和σ2MP，本文RVM模型对初始化后的α和σ2经过18次迭代后得出的模型最佳决策值gamma的取值如图4所示；

(5)判断迭代过程是否收敛或达到最大迭代次数500，若不收敛则返回第(3)步，若收敛或达到最大迭代次数则转向第(6)步；

(6)收敛最终结果权重的大小及分布如图5所示，其中的五个非零权重所对应的样本向量即是RVM模型训练所需的支持向量，删除α=肄也即图5中权值棕=0所对应的基函数；

(7)利用公式(7)对训练样本和新样本进行测试，分别根据模型的拟合精度和预测精度分析其拟合能力和泛化能力，并由训练模型所需要的相关向量数来分析其稀疏性。

图4 最佳决策值(gamma)的取值

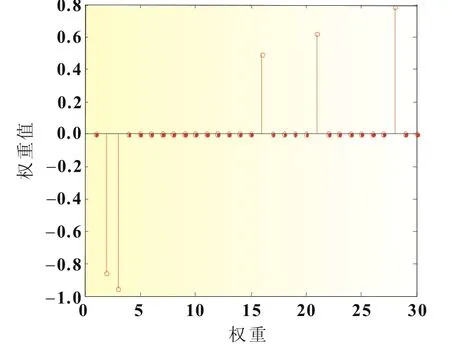
图5 权重的大小及分布

同时建立目前回归预测性能比较好的SVM模型作对比分析。SVM模型的核函数选择径向基核函数，SVM方法的实验结果对正规化参数γ和核函数参数σ2反应敏感。本实验利用交叉验证法寻优正规化参数和核函数参数得到最佳值为：γ=6.729 8，σ2=1.023 6。

3 结果分析

本文以稀疏性、拟合能力和泛化能力为标准来评定SVM模型和RVM模型性能的优劣。稀疏性好坏由支持向量个数决定，拟合能力、泛化能力则采用均方根误差和最大误差来评估。

SVM模型和RVM模型对训练样本和测试样本的拟合预测的结果如图6、图7和表2所示。由图6可知RVM模型的拟合、预测值比SVM模型更逼近真实值。为了更清楚地分析两者的拟合预测效果，图7给出了两种模型的拟合、预测相对误差曲线，由曲线可知RVM模型的预测误差小于1%，拟合误差在2%之内，拟合精度和预测精度均优于SVM模型。又结合表2中的数据可以得出如下结论：

(1)就模型的稀疏性而言，RVM模型所需支持向量个数远小于SVM模型所需支持向量个数，稀疏性良好，使得模型相对简单，从而减少了对目标值SOC的预测时间，能够为电池管理系统及时提供SOC信息。

(2)就模型的拟合能力而言，RVM模型的拟合均方根误差和拟合最大误差均小于SVM模型，说明使用贝叶斯方法的RVM模型拟合能力优于SVM模型，学习能力强。

(3)就模型的泛化能力而言，RVM模型的预测均方根误差和预测最大误差均小于SVM模型，说明RVM模型的泛化能力优于SVM模型，预测精度高，能够为电池管理系统提供更加准确的SOC信息，更适合用作蓄电池SOC预测模型。

图6 SVM和RVM拟合预测结果

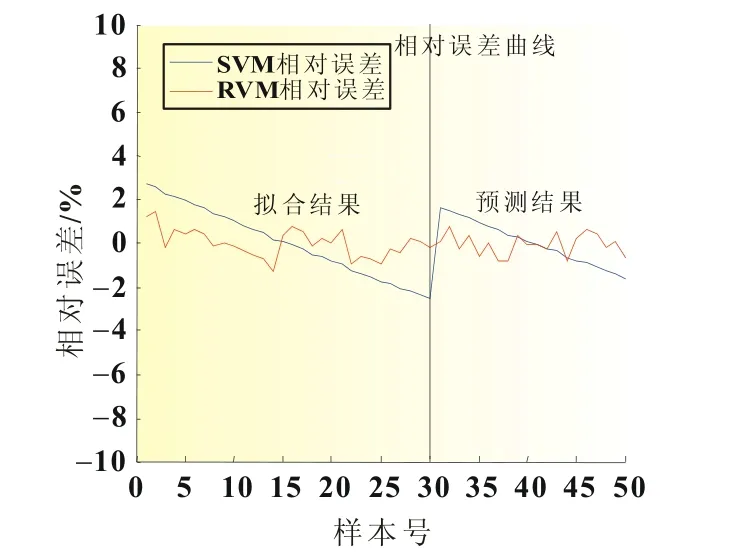
图7 SVM和RVM实验相对误差结果

表2 SVM和RVM实验结果

4 结束语

由以上实验结果可以得出，RVM方法是一种有效的预测蓄电池SOC的方法。与SVM方法相比，核函数带宽适中的RVM预测模型稀疏性良好，使得预测模型相对简单，从而减少了预测时间，同时，该模型具有较强的泛化能力，使得预测值更加准确，保证了电池能量管理系统能够提供及时准确的蓄电池SOC信息。因此，RVM模型更加适合蓄电池SOC信息的预测。

[1]TIPPING M E.Sparse Bayesian learning and the relevance vector machine[J].Journal of Machine Learning Research,2001,1(3): 211-244.

[2]高向阳,张骏,宁宁.基于相关向量机的蓄电池荷电状态预测[J].电源技术，2010，34(12):1273-1275.

[3]CHEN S,GUNN S R,HARRIS C J.The relevance vector machine technique for channel equalization application[J].IEEE Trans on Neural Networks,2002,12(6):1529-1532.

SOC prediction for battery based on relevance vector machine algorithm

HOU Jiang-na,SUN Yu-kun,WANG Peng-fei

The actual state of charge for battery was influenced by many factors,such as temperature,charge and discharge voltage,charge and discharge current and aging of battery.It was difficult to build prediction model and the prediction precision was bad.In order to solve these problems,SOC prediction for battery,based on relevance vector,was proposed.Based on charge voltage and charge current as inputs and state of charge(SOC)of battery as output,a relevance vector prediction model was presented,and the relationship between the model performance and the width of Gaussian kernel function was analyzed.According to the analysis,relevance vector machine had a better prediction when width of Gaussian kernel function was 0.9.Compared with the support vector machine(SVM), results indicate:This model had high sparseness property,reduced the prediction model complexity and prediction time.The prediction precision was enhanced,and high generalization ability was proved.

state of charge for battery;relevance vector machine;Gaussian kernel function;sparseness property; generalization ability

TM 912

A

1002-087 X(2015)03-0523-04

2014-08-10

侯江娜(1987—)，女，河南省人，硕士研究生，主要研究方向为控制理论与控制工程。