一类参数不确定非线性系统的故障检测与重构

2015-06-19王俭臣齐晓慧单甘霖

系统工程与电子技术 2015年1期

关键词：观测器气动建模

王俭臣，齐晓慧，单甘霖

（1．军械工程学院无人机工程系，河北石家庄050003；2．军械工程学院电子与光学工程系，河北石家庄050003）

一类参数不确定非线性系统的故障检测与重构

王俭臣1，齐晓慧1，单甘霖2

（1．军械工程学院无人机工程系，河北石家庄050003；2．军械工程学院电子与光学工程系，河北石家庄050003）

飞行器在全包络上表现出明显的气动参数不确定性，以某无人机纵向模型为研究对象，提出一种不确定参数在线估计的自适应观测器故障重构方法。首先，将系统状态方程描述为一类带时变参数的仿射非线性结构，在参数增广系统能观性分析基础上，采用增广容积卡尔曼滤波（augmented cubature Kalman filter，ACKF）算法实现气动参数在线估计，以克服鲁棒性死区故障检测方法的保守性，提高检测灵敏度。其次，将所估计参数用于自适应观测器设计，由于Lie导数分析方法保证了对象系统的能观性，故系统不必满足文献方法中的特定规范形式；在此基础上，给出了故障检测自适应阈值和故障参数调节律，并分析了估计误差的收敛性。仿真实验表明了所提方法的有效性。

纵向模型；参数不确定性；故障重构；增广容积卡尔曼滤波；自适应观测器

0 引言

飞控系统故障具有危害性大、对故障处理实时性要求高的特点，其诊断与容错问题一直是研究热点。按照故障部位划分，飞控系统故障主要包括执行器故障、传感器故障和系统过程故障。其中，执行器由于长期频繁地执行控制任务，是较容易发生故障的部件。至今已有大量故障诊断方法被用于飞控系统的执行器故障问题，如多模型方法［1］、未知输入观测器［2］、滑模观测器［3］、自适应观测器［4］等。但值得注意的是，文献［2- 4］的研究方法仅用于飞行器的局部线性化模型，而实际飞行过程中，飞行马赫数和环境的变化将引起气动参数时变性，从而导致飞行器模型具有明显的不确定性。为此，文献［5- 6］分别将线性参数变化（linear parameter-varying，LPV）、子空间辨识等时变建模技术用于飞控系统的执行器故障诊断问题。

自适应观测器方法由于良好的故障重构能力和适用性，近年来得到广泛研究［78］。目前，该方法的研究成果主要集中在对适用范围的拓展，例如，文献［9］和文献［10- 11］分别研究了微分同胚状态不可测、Lipschitz条件下的观测器设计问题。针对该方法的鲁棒性问题，一般方法是假定模型误差有界，并设置合理的鲁棒性检测死区；文献［12］则采用了滑模区间的鲁棒性设计。以上鲁棒性方法适用于模型误差较小的情况，对具有时变不确定性的系统，这些针对最坏情况的鲁棒性设计将表现出过分的保守性，明显降低故障检测灵敏度，甚至造成故障漏检。针对自适应观测器在不确定系统的故障诊断问题，相关研究成果较少，文献［13］研究了一类参数不确定线性系统的故障重构与调节，通过引入H∞性能指标和设计合适的故障参数调节律使状态和故障估计误差一致有界。

针对飞行控制系统的执行器故障诊断问题，研究一种参数不确定非线性系统的故障检测与重构方法。在自适应观测器基础上，通过引入不确定参数估计在线补偿系统不确定性，从而在确保故障检测鲁棒性的同时，提高检测灵敏度。另外，采用微分几何理论的能观性分析方法，保证了自适应观测器的存在性，同时避免了对象系统需要满足特定规范形式的限制。最后，对所设计自适应观测器的故障估计性能进行理论分析和仿真验证。

1 问题描述

1.1 系统建模

以某小型固定翼无人机为研究对象［14］，其水平无侧滑条件下的纵向运动模型如下：

俯仰速率微分方程

空速微分方程

攻角微分方程

俯仰角微分方程

式中，动压q－＝ρV2T／2；俯仰力矩系数CM＝CM1＋CMeδe＋CMaα＋CMq0q0，量纲为俯仰速率q0＝c－q／2VT；阻力XW＝q－SCX，阻力系数CX＝CX1＋CXαα＋CXα2α2；升力ZW＝q－SCZ，升力系数CZ＝CZ1＋CZαα；其余飞机参数及变量的含义见表1。由于各类飞机系数是随飞行状态变化的，因此运动模型具有明显的不确定性。

_表1 飞机参数及变量

实际飞行控制过程中，系统的4个状态量x＝［q，VT，α，θ］T均可直接传感测量，因此在考虑建模误差和过程扰动ηx以及测量噪声ηy情况下，模型式（5）～式（8）满足如下仿射非线性形式：

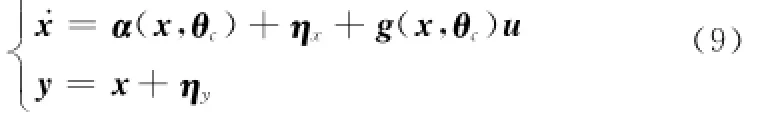
式中，θc＝［CM¯e，CMe，CX，CZ］T表示不确定气动参数；系统输入（即执行器输出）u＝［δe，FT］T；g（x，θc）表示式（5）～式（8）中与系统输入u相关的非线性向量函数，而且输入非线性部分可写成g（x，θc）u＝［g1（x，θc），g2（x，θc）］［δe，FT］T；α（x，θc）表示与系统输入无关的非线性向量函数。

1.2 问题分析

执行器故障后，以状态方程中的整个输入项作为故障项处理，例如，式（5）中的升降舵故障项为

针对所描述系统的故障检测与重构问题，假设对象系统满足如下几个条件：

假设1 故障发生后，系统状态仍保持有界。

假设2 建模误差和过程扰动ηx及测量噪声ηy是有界的，即存在|ηx|≤¯ηx、|ηy|≤¯ηy。

假设3 系统的非线性部分满足Lipschitz条件，即|α（x1，θc）－α（x2，θc）|≤γ1|x1－x2|，|g（x1，θc）u－g（x2，θc）u|≤γ2|x1－x2|。

假设4 故障项的变化率大于不确定性参数引起的模型最大变化率，即

根据飞行动力学，飞机气动系数可描述为飞行马赫数的函数，对于非强机动飞行而言，气动系数的变化能够满足此假设。

2 不确定参数在线估计

根据飞行器建模理论，全包络分段线性化或子空间辨识等方法能够实现在线近似建模，从而避免过大的鲁棒性死区，但这类局部线性化方法存在一定的建模误差。例如，文献［6］在子空间辨识基础上，进一步采用径向基函数（radial basis function，RBF）神经网络补偿系统非线性部分和建模不确定性。

将飞行器建模视为“灰箱”问题，在根据飞行动力学建立模型结构基础上，利用飞行数据进行气动参数辨识成为近年来飞行器设计、建模及控制领域的研究热点。相比局部建模方法，该方法具有更好的实时性，同时具有较高的模型辨识精度。目前常用的气动参数辨识方法包括最小二乘法［15］、极大似然法［16］、Kalman滤波［17］等。本文将增广容积卡尔曼滤波（augmented cubature Kalman filter，ACKF）算法用于不确定气动参数在线估计，基本思想是利用不确定参数构造增广系统，然后采用容积卡尔曼滤波（cubature Kalman filter，CKF）算法实现系统状态与不确定参数联合估计。相比传统建模方法，ACKF算法具有非线性、实时性等优点，可获得更高的模型跟踪精度。但需要指出，该方法的前提是参数增广系统是能观的。

2.1 参数增广系统能观性分析

对如下形式的非线性系统：

定义与输出相关的Lie导数能观性矩阵

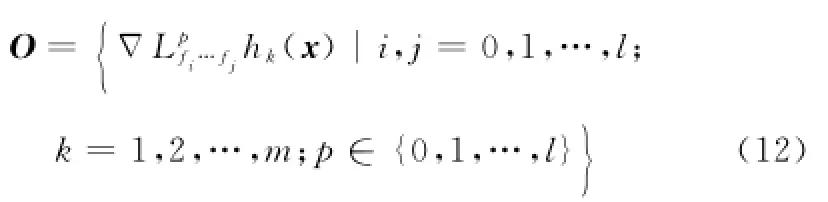
定理1［18］如果能观性矩阵O满足rank（O）＝n，则式（11）的非线性系统是局部弱能观的。

将式（9）中的不确定参数θc增广为系统状态，即X＝［x，θc］T，并引入状态辅助方程

可得增广后的系统方程为

对应于式（9）中，f0（X）＝α（X），f1（X）＝g1（X），f2（X）＝g2（X），［u1，u2］＝u＝［δe，FT］。

根据Lie导数理论［19］，计算式（15）中h1（X）、h2（X）、h3（X）、h4（X）的零阶Lie导数

相应的Lie导数梯度为Δ

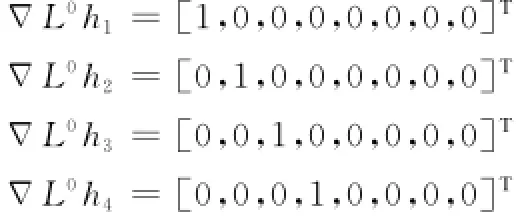
计算h1（X）、h2（X）、h3（X）、h4（X）的一阶Lie 导数相应的Lie导数梯度为

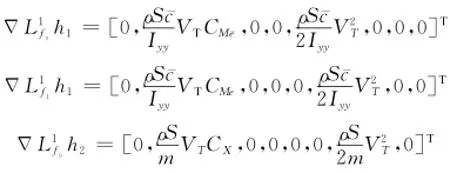
至此，可构造如下系统能观性矩阵：

显然，若飞机空速量VT≠0，必有rank（O）＝8，因此本文的参数增广系统是局部弱能观的。

2.2 气动参数在线估计

CKF算法［20］采用数值积分方法直接计算非线性变换后随机变量的均值和协方差，具有比扩展卡尔曼滤波（extended Kalman filter，EKF）和无迹卡尔曼滤波（unscented Kalman filter，UKF）算法更好的非线性逼近能力、数值精度及滤波稳定性［21］；而相比非线性的粒子滤波（particle filter，PF）算法，其计算量大大降低，且不存在粒子贫化的不足。采用ACKF算法的系统状态与不确定气动参数联合估计过程如下：

（1）对参数增广系统进行能观性分析和近似离散化；确定初始状态估计值^x0|0和协方差阵P0|0，其中P0|0＝S0|0ST0|0。注意，本小节采用x表示系统增广状态，而X表示下文中的Cubature点。

（2）时间更新

步骤1 计算Cubature点

式中，i＝1，2，…，m，m＝2nx，nx为状态维数；参数ξi的计算公式为

式中，ei为第i个元素为1，其余元素为0的基本单位向量。

步骤2 通过增广系统状态方程传播Cubature点

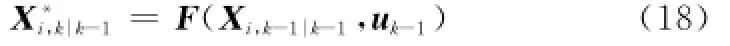
式中，F（·）表示式（14）的增广系统状态方程。步骤3 计算状态一步预测值

步骤4 计算预测误差方差阵

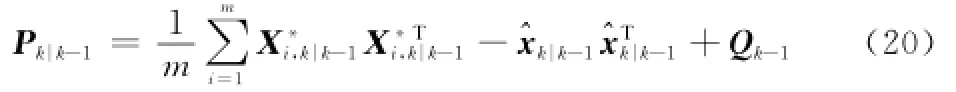
式中，Q表示过程噪声方差阵。

（3）量测更新

步骤1 计算Cubature点

步骤2 传播Cubature点

步骤3 计算量测预测值

步骤4 计算新息协方差阵

式中，R表示测量噪声方差阵。

步骤5 计算互协方差阵

步骤6 计算增益阵

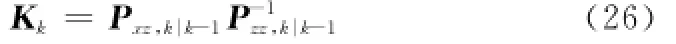
步骤7 更新状态估计量

步骤8 计算误差协方差阵

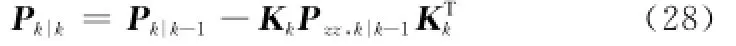
3 采用自适应观测器的故障重构

自适应观测器利用观测误差不断调节故障估计器参数，从而使故障估计误差不断减小。该方法重点研究如下一类非线性系统：

式中，β（t－T0）为故障时间函数；f（y，u）为故障大小。文献中一般要求对象系统的线性部分（A，C）必须能观，非线性部分l（y，u）仅是输入、输出的函数（称为规范形式），从而保证整个系统的能观性。由第2节可知，本文的参数增广系统是能观的，因此原系统必然能观，从而系统不必满足上述规范形式。

3.1 自适应观测器设计

对式（9）所示非线性系统，当第i个执行器故障时，根据式（10）得

式中，u为执行器无故障时的理想输出；ui为u的第i个分量；ufault，i表示ufault的第i个分量。

采用RBF神经网络作为故障估计器，由神经网络的任意逼近性可知［22］，存在最优的网络权重w*使得

式中，φ（·）为RBF核函数；v为有界小量；^x为观测器状态估计值；^θc为不确定参数的滤波估计值。在不确定参数在线估计基础上，构造如下自适应观测器：

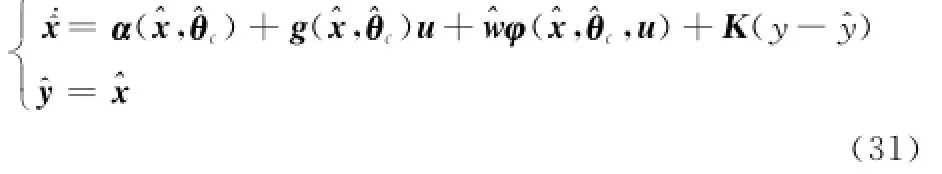
式中，K∈Rn×n为反馈增益阵；^w为故障估计器待整定参数。令K＝k I，~w＝w*－^w，由式（30）和式（31）可得观测器误差方程为

假设5 采用ACKF算法的不确定参数估计误差是有界的。

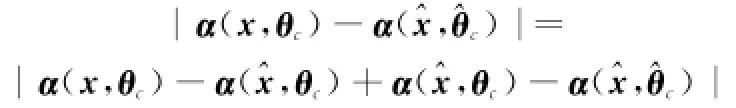
根据假设3和假设5，则存在有界常数¯ηα使得|α（x，θc）－成立。同理，存在有界常数使得成立。

无故障发生时，神经网络故障估计器输出为零。在观测器初始误差e（0）＝0条件下，求解式（32）的微分方程，得

因此，采用如下自适应的鲁棒性故障检测阈值：

若观测器输出残差|ey|小于式（33）的检测阈值，系统无故障发生；反之则系统发生故障。

3.2 故障估计的收敛性分析

定理2 故障发生后，若进一步采用如下的故障估计参数调节律

则观测器输出残差ey和故障参数估计误差~w是最终一致有界的，即ey∈L∞，~w∈L∞。式中，Γ为参数学习率，满足正定对称条件；D［ey］为死区算子，当|ey|小于检测阈值时取值为0，反之取值为ey。

证明故障发生后，取系统式（32）的Lyapunov函数为

则有

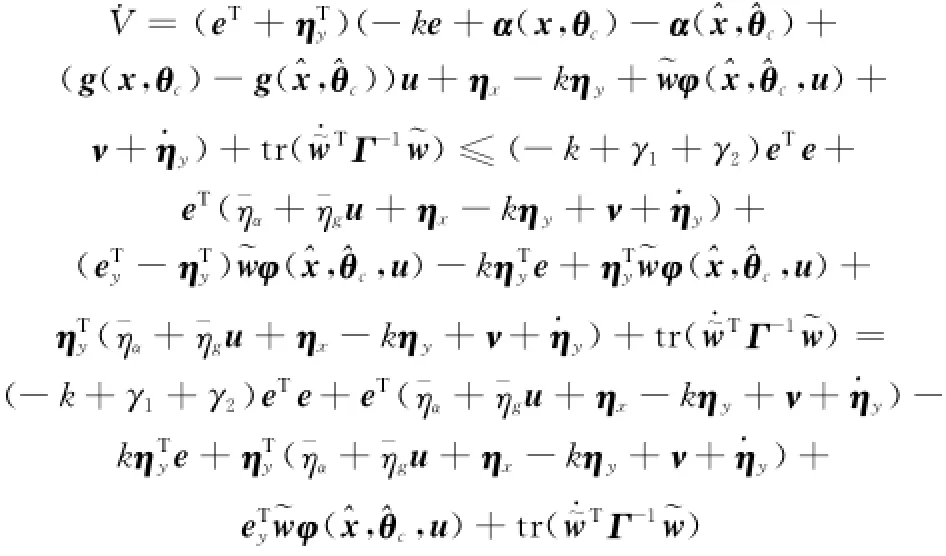
由

又因为

取观测器反馈增益系数k＞2（γ1＋γ2＋1），因此当

时，有˙V＜0。由于不等式右端各类不确定性及系统输入均是有界的，因此采用式（31）的自适应观测器和式（34）的故障估计参数调节律得到的观测器输出残差和故障估计误差一致有界。证毕

在对故障项f（x，θ，u）估计基础上，可进一步得到故障执行器偏差量（故障大小）的估计

4 仿真实验

利用本文第1节所描述的无人机纵向运动模型，验证如下飞行控制过程：目标运动状态xgoal＝［q，v，α，θ］＝［0，16，0.053 5，0.053 5］；初始运动状态xinit＝［q，v，α，θ］＝［0，30，0.042 5，0.042 5］；系统的反馈增益矩阵为

由于文献［14］未给出具体的气动参数变化曲线，不妨假设如下的变化规律：

式中，sat［·］为线性饱和特性函数。另外，取增广系统过程噪声协方差矩阵P＝10－4diag（0.01，1，0.01，0.01，0.01，1，4，0.1），表示过程噪声和建模误差等外扰；取测量噪声协方差矩阵Q＝10－4diag（0.01，1，0.01，0.01），表示传感器测量噪声。

4.1 不确定参数估计

取系统初始协方差P0＝0.1I8，无故障情况下，采用ACKF算法获得的不确定气动参数的估计效果如图1所示。由实验结果看出，ACKF算法能较好地跟踪不确定气动参数的实时变化。

4.2 故障量估计

在不确定参数在线估计基础上进一步验证本文方法的故障检测与估计性能。构造如式（31）所示的自适应观测器，其中观测增益阵K＝20I4，根据系统外扰设置和第4.1节的滤波估计效果，按照式（33）确定如下的自适应故障检测阈值：

由式（6）和式（7）可知，攻角状态方程对发动机推力故障的敏感性明显低于空速状态方程，因此对发动机故障的检测与估计通过空速状态观测残差来实现。

采用单层RBF神经网络作为故障估计器。对于升降舵故障，估计器输入量为空速量VT，估计器包含11个神经元，神经元中心在区间［15，30］上均匀分布，核宽度为20，网络参数学习率Γ＝10－8；对于发动机推力故障，估计器输入量为攻角α，估计器包含11个神经元，神经元中心在区间［0.02，0.1］上均匀分布，核宽度为0.1，网络参数学习率Γ＝1。

为对比说明本文方法的有效性，将带有遗忘因子的递推子空间辨识算法用于在线建模，其中遗忘因子β取0.95。在此基础上，可构造故障估计所用的自适应观测器，并采用与本文方法相同参数设置的单层RBF网络作为故障估计器。下文中称该方法为“对比方法”。通过仿真实验，选取对比方法的故障检测阈值ε＝［0.035，0.035，0.003，0.005］T。

仿真1 升降舵卡死故障

在仿真时间10 s时设置δefault＝0．05 rad，故障持续时间为0．1s。按照式（30）和式（35），故障估计器的目标估计值为－δe＋δefault，其中δe为舵面理想输出值。两种方法获得的观测器输出残差和故障估计结果如图2所示。

图2 升降舵卡死故障仿真结果

仿真2 发动机偏差故障

在仿真时间10 s时设置FTfault＝FT＋ΔF，其中FT为发动机理想输出值，ΔF＝30 N为偏差值（当发动机传感器发生测量偏差时，可能导致此类故障），故障持续时间为1 s。此时，故障估计器的目标估计值为－FT＋FTfault＝ΔF。采用本文方法获得的观测器输出残差和故障估计结果如图3所示，而采用对比方法时，由于故障所引起的输出残差未能达到故障检测阈值，从而发生了故障漏警。

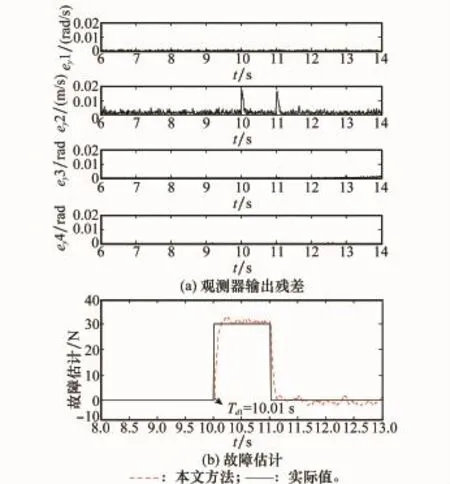
图3 发动机偏差故障仿真结果

对比图2（a）中的实验结果可知，无故障注入情况下，本文的不确定参数估计方法具有更小的观测器输出残差，体现了所提方法良好的在线建模性能。此外，由图2（b）、图3（b）的故障估计结果可以看出，在一定的收敛误差容许条件下，所设计的故障参数调节律具有满意的故障估计能力。但对比图2（b）中两种方法的故障估计结果发现，更高的建模精度保证了本文方法具有更好的故障检测灵敏度，从而可获得更准确的故障估计结果。

5 结论

针对飞行器气动参数的时变性，提出了一种参数不确定非线性系统的自适应观测器故障检测与重构方法，文章的主要工作和结论如下：

（1）将ACKF算法用于不确定参数在线估计，从而克服传统故障检测算法直接采用鲁棒性死区带来的保守性。而相比局部线性化的处理方法，滤波估计方法不需要气动参数变化的先验知识，同时避免了线性化误差。

（2）采用微分几何理论的Lie导数方法分析对象系统的能观性，保证了参数估计方法的可行性，同时有利于自适应观测器的设计，避免了系统需要满足特定规范形式的限制。

（3）在参数估计误差有界假设条件下，通过对观测误差系统构造Lyapunov能量函数，分析了观测器残差和故障估计误差的收敛性，仿真实验也表明了方法的可行性。

［1］Seungkeun K，Jiyoung C，Youdan K．Fault detection and diagnosis of aircraft actuators using fuzzy-tuning IMM filter［J］．IEEE Trans. on Aerospace and Electronic Systems，2008，44（3）：940- 952．

［2］Wang D，Lum K Y．Adaptive unknown input observer approach of aircraft actuator fault detection and isolation［J］．International Journal of Adaptive Control and Signal Processing，2007，21（1）：31- 48．

［3］Tan C P，Crusca F，Aldeen M．Extended results on robust state estimation and fault detection［J］．Automatica，2008，44（8）：2027- 2033．

［4］Fan J H，Zhang Y M，Zheng Z Q．Adaptive observer-based integrated fault diagnosis and fault-tolerant control systems against actuator faults and saturation［J］．Journal of Dynamic Systems，Measurement，and Control，2013，135（4）：041008．

［5］Halim A，Christopher E．Robust actuator fault reconstruction for LPV systems using sliding mode observers［C］∥Proc.of the 49th IEEE Conference on Decision and Control，2010：84- 89．

［6］Zhang Z D，Hu SS．A new method for fault prediction of modelunknown nonlinear system［J］．Journal of the Franklin Institute，2008，345（2）：136- 153．

［7］Zhang K，Jiang B．Fault diagnosis observer-based output feedback fault tolerant control design［J］．Acta Automatic Sinica，2010，36（2）：274- 281．（张柯，姜斌．基于故障诊断观测器的输出反馈容错控制设计［J］．自动化学报，2010，36（2）：274- 281．）

［8］Liao Y，Wu B，Cao D G，et al．Modeling and simulation ofprocess of propellant refueling to space stations［J］．Journal of System Simulation，2011，23（3）：618- 621．（廖瑛，吴彬，曹登刚，等．基于自适应观测器的导弹电动舵机故障诊断研究［J］．系统仿真学报，2011，23（3）：618- 621．）

［9］Chen M，Tong C N，Zhang S Y．Intelligent fault diagnosis for a class of affine nonlinear system［J］．Control and Decision，2011，26（2）：221- 226．（陈明，童朝南，张士勇．一类仿射型非线性系统智能故障诊断［J］．控制与决策，2011，26（2）：221- 226．）

［10］Zhang X D，Polycarpou M M，Thomas P．Fault diagnosis of a class of nonlinear uncertain systems with Lipschitz nonlinearities using adaptive estimation［J］．Automatica，2010，46（2）：290- 299．

［11］Zhang X D．Sensor bias fault detection and isolation in a class of nonlinear uncertain systems using adaptive estimation［J］．IEEE Trans.on Automatic Control，2011，56（5）：1220- 1226．

［12］He J，Zhang C F．Robust diagnosis of incipient faults based on sliding mode observer［C］∥Proc.of the 8th World Congress on Intelligent Control and Automation，2010：6- 9．

［13］Gao Z F，Jiang B．Fault accommodation for a class of linear time-varying systems with parametric uncertainties［J］．Systems Engineering and Electronics，2009，31（12）：2924- 2928．（高志峰，姜斌．一类参数不确定的线性时变系统的故障调节［J］．系统工程与电子技术，2009，31（12）：2924- 2928．）

［14］Ducard G J J．Fault-tolerant flight control and guidance systemspractical methods for small unmanned aerial vehicles［M］．London：Springer-Verlag，2009．

［15］Sun Y，Duan G R，Zhang M R，et al．Modified aerodynamic coefficient models of hypersonic vehicle in reentry phase［J］．Systems Engineering and Electronics，2011，31（1）：134-137．（孙勇，段广仁，张卯瑞，等．高超声速飞行器再入过程改进气动系数模型［J］．系统工程与电子技术，2011，31（1）：134- 137．）

［16］Qian W Q，Wang Q，Wang W Z，et al．Application of genetic algorithms for aerodynamic parameter estimation［J］．Acta Aerodynamica Sinica，2003，21（2）：196- 201．（钱炜祺，汪清，王文正，等．遗传算法在气动力参数辨识中的应用［J］．空气动力学学报，2003，21（2）：196- 201．）

［17］Yu S J，Cheng Y Q，Qian W Q．Research on transonic aerodynamic parameter online identification［J］．Journal of Astronautics，2011，32（6）：1211- 1216．（余舜京，程艳青，钱炜祺．跨声速气动参数在线辨识方法研究［J］．宇航学报，2011，32（6）：1211- 1216．）

［18］Zhou X S，Stergios I R．Robot-to-robot relative pose estimation from range measurements［J］．IEEE Trans.on Robotics，2008，24（6）：1379- 1393．

［19］Guo L，Cheng D Z，Feng D X．Introduction to control theoryfrom basic concept to research fronts［M］．Beijing：Sciences Press，2005．（郭雷，程代展，冯德兴．控制理论导论——从基本概念到研究前沿［M］．北京：科学出版社，2005．）

［20］Arasaratnam I，Haykin S．Cubature Kalman filters［J］．IEEE Trans.on Automatic Control，2009，54（6）：1254- 1269．

［21］Arasaratnam I，Haykin S，Hurd T R．Cubature Kalman filtering for continuous-discrete systems：theory and simulations［J］．IEEE Trans.on Signal Processing，2010，58（10）：4977- 4993．

［22］Liu C S，Hu S S．Fault diagnosis based on adaptive neural networks for a class of nonlinear systems［J］．Systems Engineering and Electronics，2007，29（4）：665- 668．（刘春生，胡寿松．基于自适应神经网络的非线性系统故障诊断［J］．系统工程与电子技术，2007，29（4）：665- 668．）

Fault detection and reconstruction for a class of nonlinear systems with parametric uncertainties

WANG Jian-chen1，QI Xiao-hui1，SHAN Gan-lin2
（1.Department of Unmanned Plane Engineering，Ordnance Engineering College，Shijiazhuang 050003，China；2.Department of Electronics and Optics Engineering，Ordnance Engineering College，Shijiazhuang 050003，China）

Aiming at the obvious aerodynamic parametric uncertainties of aircraft in the full flight envelope，a fault reconstruction method based on a modified adaptive observer is proposed．The adaptive observer is improved by the uncertain parameter estimation process and validated on the longitudinal model of some unmanned vehicle．According to this method，the longitudinal model is described as an affine nonlinear structure with time variant parameters，and the observability of its parameter-augmented model is analyzed．On this basis，to deal with conservatism of the robustness dead zone technique in fault detection and refine the detection sensitivity，aerodynamic parameters are identified on line by the augmented cubature Kalman filter（ACKF）algorithm．Then the parameter estimations are adopted in adaptive observer design．As the Lie derivative based criterion guarantees observability of the object system，the literature restriction that the object system must be within some particular structure is avoided．Based on this，the adaptive fault detection threshold and the fault parameter regulation law are derived，and the convergency of the estimation error is analyzed．Finally，simulations are conducted to testify the availability of this method．

longitudinal model；parametric uncertainty；fault reconstruction；augmented cubature Kalman filter（ACKF）；adaptive observer

TP 273

10．3969／j．issn．1001-506X．2015．01．25

王俭臣（1987-），男，博士研究生，主要研究方向为飞控系统故障诊断。

E-mail：wangjch2005＠163．com

齐晓慧（1962-），女，教授，博士，主要研究方向为自修复控制、最优控制。

E-mail：qi-xh＠163．com

单甘霖（1962-），男，教授，博士，主要研究方向为故障诊断、信息融合技术。

E-mail：shanganlin＠163．com

1001-506X（2015）01-0155-08

网址：www．sys-ele．com

2013- 12- 17；