服务航天器超近程逼近目标的相对姿轨耦合控制

2015-06-19张庆展靳永强康志宇肖余之

系统工程与电子技术 2015年1期

关键词：航天器姿态动力学

张庆展，靳永强，康志宇，肖余之

（上海宇航系统工程研究所，上海201109）

服务航天器超近程逼近目标的相对姿轨耦合控制

张庆展，靳永强，康志宇，肖余之

（上海宇航系统工程研究所，上海201109）

针对服务航天器超近程逼近目标的相对姿态轨道耦合控制问题，推导了耦合动力学模型并设计了相应控制律。通过引入描述相对运动构型变化的期望相对位置矢量和位置误差矢量，将相对轨道跟踪控制问题转化为调节器的设计问题。推导了考虑对接机构安装位置的相对姿态轨道耦合动力学模型。利用李雅普诺夫稳定性理论，设计了考虑未知有界干扰的相对姿态轨道耦合控制律。考虑控制输入受限进行数学仿真，结果表明所设计的控制律是有效的，并具有较好的性能。

在轨服务；相对姿轨；耦合控制；动力学；期望相对位置矢量

0 引言

在轨服务是通过一系列综合在轨操作使在轨运行航天器的能力得到改善的过程［1］。服务航天器通过对目标在轨燃料补加、在轨维修或捕获清除等服务操作，延长目标在轨寿命、提升工作能力或减少空间碎片数量。执行上述操作的关键是服务航天器完成与目标的逼近至对接任务。在超近程逼近目标至对接过程中，需控制服务航天器使其沿目标被动对接口方向逼近，同时跟踪目标的姿态，使其主动对接口沿逼近方向指向被动对接口。显然，逼近过程中的相对位置和姿态是耦合的，其耦合性主要体现在：服务航天器期望相对位置随目标航天器的姿态变化而变化［2］；服务航天器执行机构产生的推力与目标航天器及其自身的姿态都有关。

相对姿轨耦合控制的研究是伴随服务操作任务的需求提出的：文献［3］采用T-H方程描述相对动力学模型，是较成熟的方法；文献［4］以非线性轨道动力学描述航天器之间的相对运动，参考轨道为圆轨道；文献［5］针对卫星的编队飞行问题，推导了追踪星相对目标星的姿轨耦合动力学模型，并设计自适应跟踪控制律；文献［6- 7］针对航天器的绕飞任务设计了姿态或轨道的跟踪控制律；文献［8］针对交会对接问题，考虑参数不确定性，设计了相对姿轨输出反馈控制律；文献［9］设计了航天器间接近操作的最优控制律；文献［10- 11］研究了卫星近距离相对运动的姿轨同步问题，并设计相应的姿轨跟踪控制律；文献［12］研究了接近翻滚目标的最优控制问题。上述研究在相对动力学建模中未考虑航天任务中对相对运动构型设计需求的灵活性，并且多是基于航天器间相对运动的跟踪控制来设计控制律的。

本文综合考虑在轨服务操作任务的多样性及对相对运动构型需求的灵活性，引入了描述相对运动构型变化的期望相对位置矢量和位置误差矢量。通过此矢量描述的相对轨道误差动力学方程将相对轨道跟踪控制转化为调节器设计。考虑对接装置安装位置，建立了相对姿轨耦合动力学模型。基于此动力学模型设计了考虑姿轨耦合及未知有界干扰的控制律。考虑工程实际中控制量受限的约束，仿真中对控制加速度和力矩进行向量限幅。

1 问题描述

服务航天器超近程逼近目标的过程中，需要同时控制其相对目标的位置和姿态，来保证两对接装置之间的相对状态满足捕获条件。为方便问题描述，定义以下坐标系：①地心惯性坐标系（OiXiYiZi）原点Oi位于地心，OiXi轴指向春分点，OiZi轴与地球的自转轴一致，OiYi轴与OiXi、OiZi轴形成右手系；②相对轨道坐标系（OTXTYTZT）原点OT位于目标质心，OTXT轴沿地心与目标质心连线方向背离地心，OTYT轴在轨道平面内指向目标飞行方向，OTZT轴与OTXT、OTYT轴形成右手系；③ObtXbtYbtZbt和ObsXbsYbsZbs分别表示目标和服务航天器的本体坐标系。

1.1 相对轨道动力学

图1为服务航天器与目标的相对位置关系示意图，图中，rt、rs分别为目标、服务航天器的位置矢量；l为服务航天器相对目标的位置矢量；ld为服务航天器的期望相对位置矢量；Δr为服务航天器实际位置与期望位置之间的位置误差矢量。则有关系式

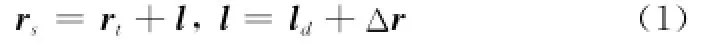
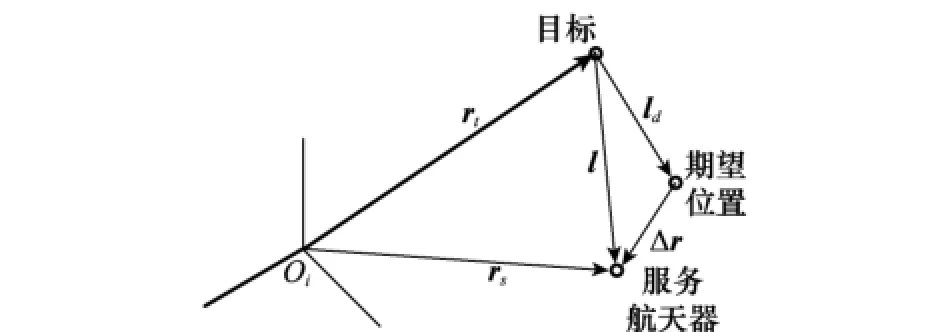
图1 服务航天器与目标的相对位置关系示意图

由服务航天器与目标在惯性系下的轨道动力学方程相减，并结合式（1）可得

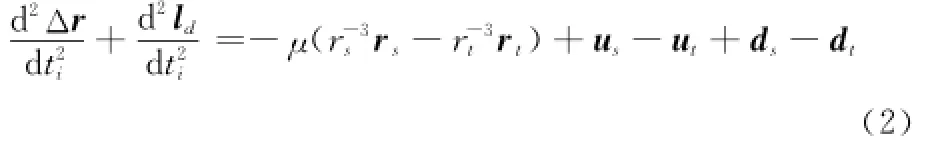
式中，d／d ti表示在惯性系中的导数；μ为地球引力常数；ut为目标的机动加速度矢量；us为服务航天器的控制加速度矢量；dt、ds分别为目标、服务航天器的摄动加速度矢量。

由式（2），并结合矢量在动坐标系中的求导公式，在相对轨道坐标系中建立服务航天器对目标的相对轨道误差动力学模型

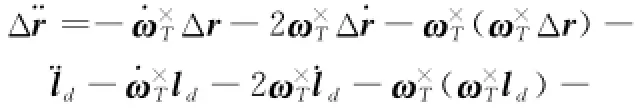
式中，Δ¨r、Δ˙r和¨ld˙、ld分别为Δr和ld在相对轨道系中的导数；ωT×为ωT的反对称矩阵，且ωT＝［0 0˙ft］T为相对轨道系相对惯性系的角速度，˙ft为目标真近点角ft的导数；ubs为服务航天器本体系中的控制加速度矢量；RTs为服务航天器本体系到相对轨道系的坐标转换矩阵；uTt、dTs和dTt分别为ut、dt和ds在相对轨道系中的表示。由式中RTsubs可见，服务航天器执行机构在本体系中产生的控制加速度与目标及自身姿态之间存在着耦合。

对于任意的a∈R3，a×定义为

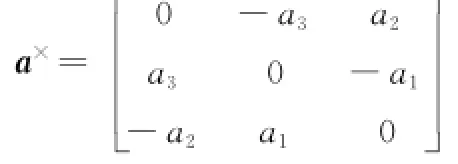
令

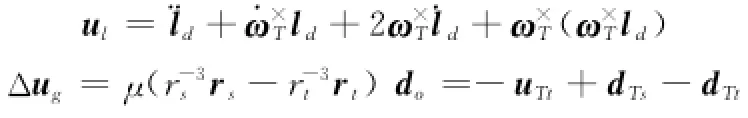
则由式（3）表示的相对轨道误差动力学模型可转化为

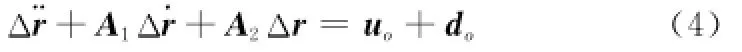
式中

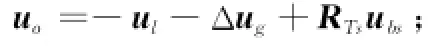
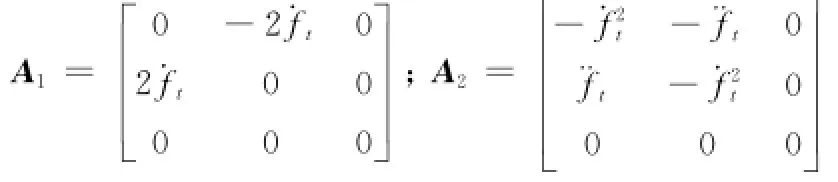
对航天器间的相对运动而言，ld描述了期望相对运动构型的变化。相对运动的轨道控制实质上是状态跟踪控制，式（4）是由位置误差Δr描述的相对轨道误差动力学方程，它的平衡状态是零状态。本文引入由ld和Δr建立的相对轨道误差动力学方程，把状态跟踪控制转化为了调节器设计。这样做的好处是：期望相对位置矢量和位置误差矢量将航天器间的相对运动控制分解为描述相对运动构型变化的期望相对位置矢量ld的设计和由位置误差矢量Δr描述的二阶系统调节器的设计，简化问题的描述和控制。

服务航天器超近程逼近目标至对接的相对轨道控制与通常意义的轨道控制有区别。轨道控制一般是控制航天器的质心运动，而超近程逼近目标至对接的轨道控制是控制两航天器对接装置之间的相对运动状态。图2为捕获装置间的相对位置示意图。

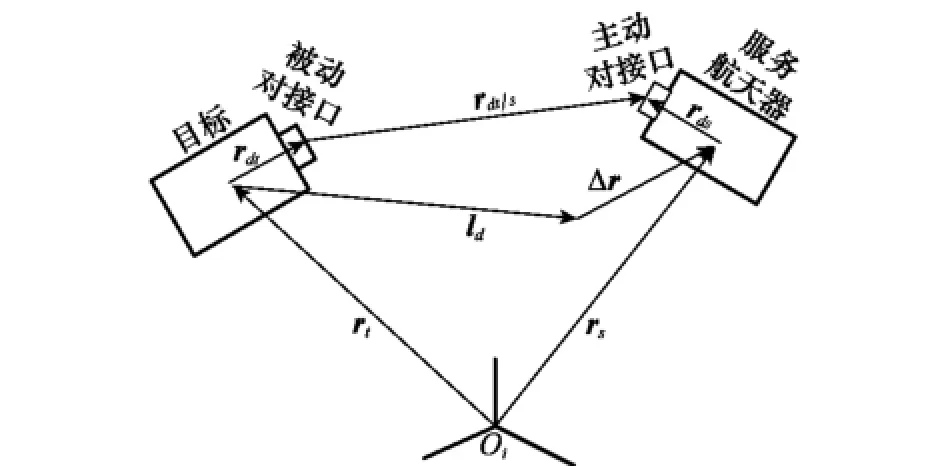
图2 对接装置间的相对位置关系示意图

图2中，rdt、rds分别为目标、服务航天器对接装置在本体系中的安装矢量；rdt／s为两航天器对接装置间在相对轨道系中的位置矢量。则在相对轨道坐标系中有

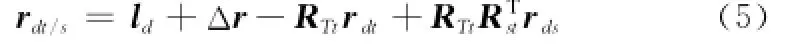
式中，RTt、Rst分别为目标航天器本体坐标系到相对轨道坐标系、服务航天器本体坐标系的坐标转换矩阵。

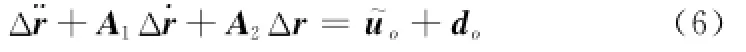
1.2 相对姿态运动学和动力学

采用修正罗德里格参数（modified Rodrigues parameters，MRP）作为姿态描述参数，则服务航天器相对目标的姿态运动学方程［1314］为

式中，，其中σst为服务航天器本体系相对目标本体的姿态，I3×3为3×3维的单位矩阵；ωst＝ωs－Rstωt为服务航天器本体系相对目标本体系的姿态角速度，其中ωt、ωs分别表示目标、服务航天器本体系相对惯性系的姿态角速度。

对式（7）求导，并联合欧拉方程描述的姿态动力学方程，可建立服务航天器相对目标的姿态动力学方程为

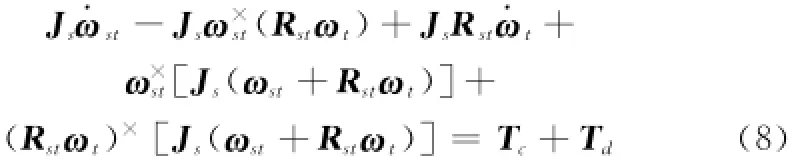
式中，利用了等式˙Rst＝－ω×stRst。

对式（7）求导，并联合式（8）进一步可得以¨σst表示的相对姿态动力学方程

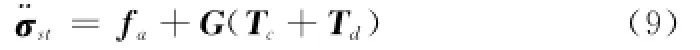
式中

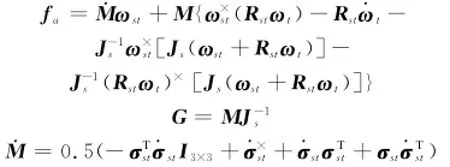
由式（6）和式（9）表示的相对位置误差和姿态动力学模型可知，控制系统的目的是设计相对轨道和姿态控制律，使Δr→0，Δ˙r→0，σst→0，˙σst→0。

2 相对姿轨耦合控制律设计

为方便相对姿轨耦合控制律设计，建立服务航天器相对目标的姿轨一体化耦合动力学模型。选取状态x＝［ΔrTσTst］T，结合式（6）和式（9）建立相对姿轨一体化耦合动力学模型

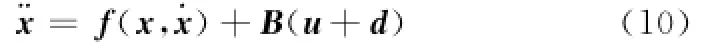
式中

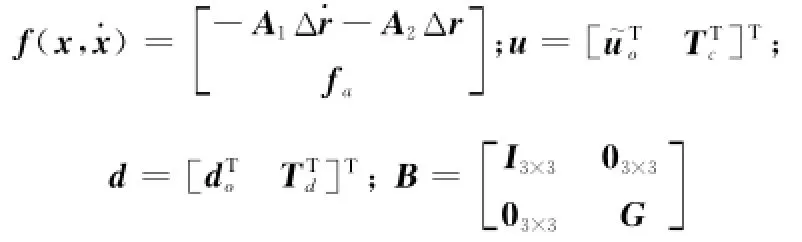
由式（10）可知，控制系统的目的是设计相对姿轨一体化耦合控制律，使

假设系统存在未知有界干扰，即

式中，di（i＝1，2，…，6）分别为干扰的分量；dmax为干扰的上界。为了获得较好的控制性能，增加对未知干扰的估计，设计控制律u为

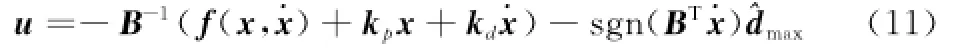
式中，kp、kd为正定对称矩阵；sgn（·）为符号函数，且对于，定义

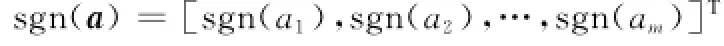
稳定性证明如下：

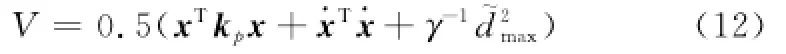
式中，γ为大于零的常数。

对V沿状态轨迹求导，可得

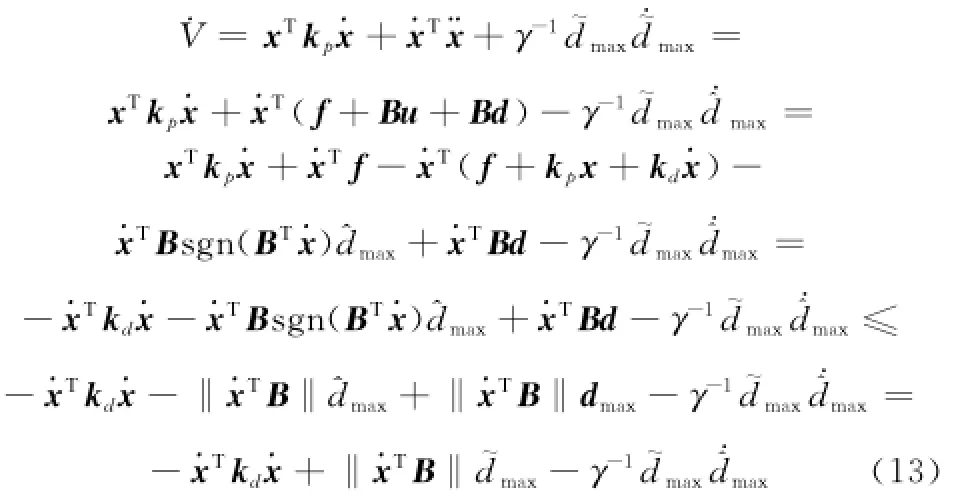
选取干扰的自适应律

将式（14）代入式（13），可得

由˙V≤0，可知V有界，故x、˙x有界。由式（10）可知¨x有界。则¨V＝－2˙xTkd¨x有界，因此˙V一致连续。由Barbalat引理可知，˙V→0，˙x→0。考虑到闭环系统式（10），当t→∞时，x→0。因此当t→∞时，x→0，˙x→0，且当‖x‖→∞时，V→∞，所以由李雅普诺夫稳定性定理可知，闭环系统全局渐近稳定［15-16］。证毕

可得作用在服务航天器本体的控制加速度为

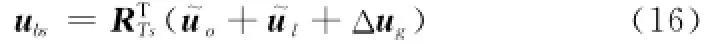
3 数学仿真

考虑工程实际约束，为了使控制输入不超出实际的可用执行机构最大输出，对控制加速度ubs和力矩Tc分别进行向量限幅［2，17］。定义

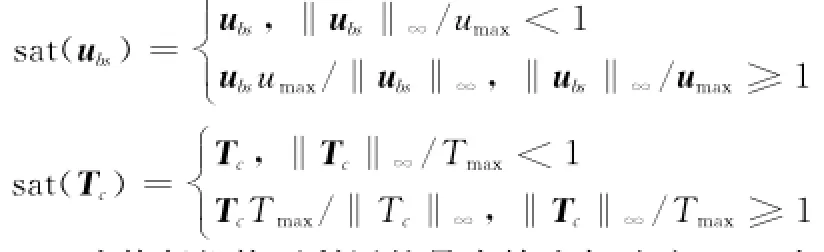
式中，umax为执行机构可利用的最大输出加速度；Tmax为执行机构可利用的最大输出力矩；其中ubsj和Tcj分别为ubs和Tc的分量。

假设闭环系统受到的干扰［18］具有如下形式：

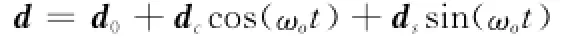
式中，d0、dc和ds为未知的干扰幅值；ωo为轨道角速度。

选择目标为地球同步轨道的航天器，服务航天器初始位置在目标后方150 m处，以0．1 m／s的速度沿直线逼近目标。服务航天器的转动惯量矩阵为

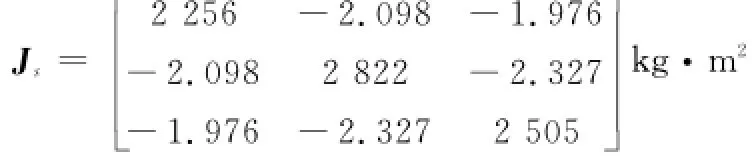
其他仿真参数见表1。表中，at、et、it、Ωt、ωt和ft为目标航天器的初始轨道根数；ld0和˙ld0分别为服务航天器期望相对位置矢量的初值和逼近目标的速度；Δr0和Δ˙r0分别为服务航天器的初始位置误差和速度误差；σst0为服务航天器的初始姿态误差；do0、doc和dos为相对干扰加速度幅值；Td0、Tdc和Tds为作用在服务航天器上的干扰力矩幅值。

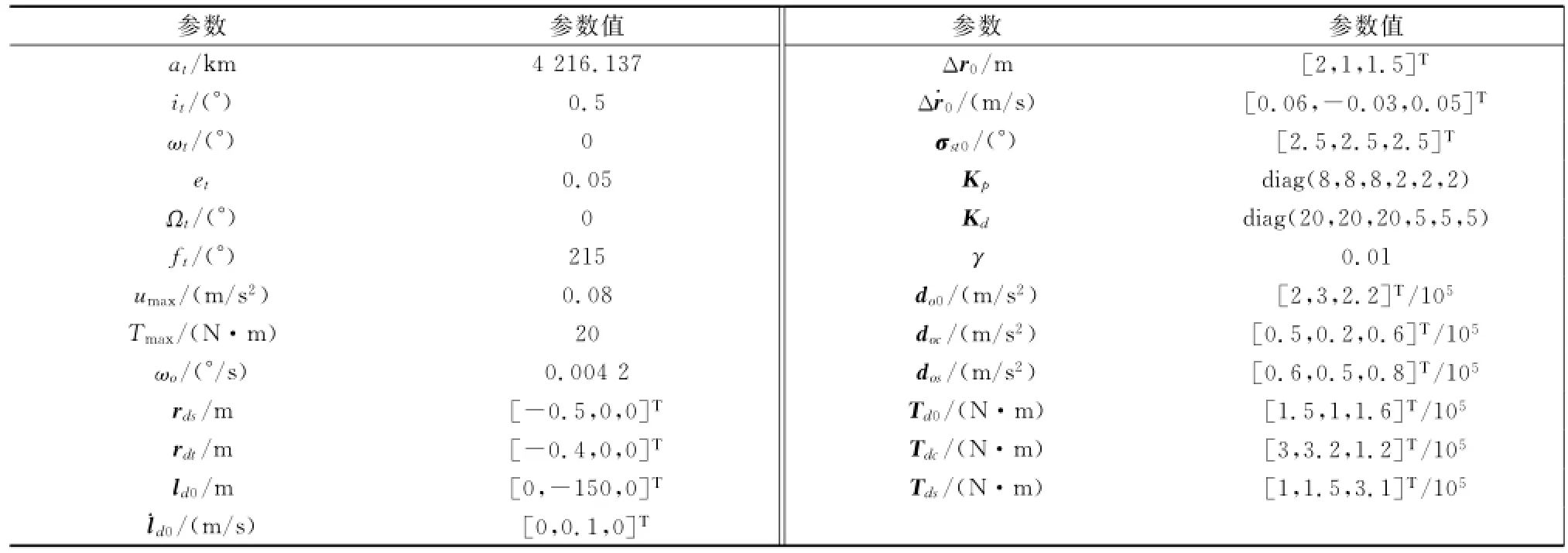
表1 仿真参数

利用上述仿真参数，得仿真结果如图3～图7所示。图中，rx、ry、rz为对接装置间相对位置rdt／s的分量；Vx、Vy、Vz为对接装置间相对速度˙rdt／s的分量；Δrx、Δry、Δrz为对接装置间相对位置跟踪误差Δr的分量；ΔVx、ΔVy、ΔVz为对接装置间相对速度跟踪误差Δ˙r的分量；d1、d2、d3、d4、d5和d6为估计误差d～的分量。

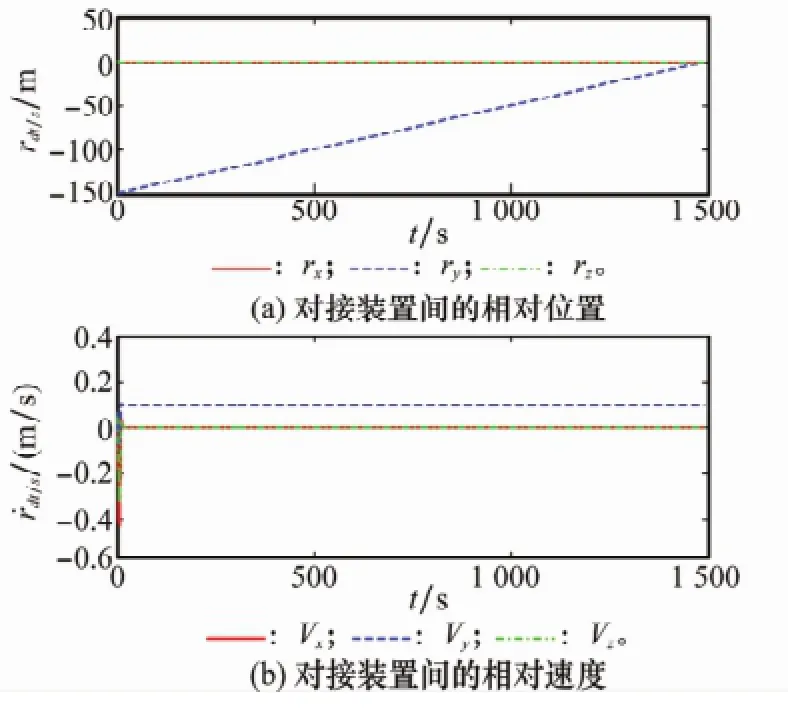
图3 对接装置间的相对位置和速度（OTXTYTZT）

为减小式（11）中符号函数引起的抖振问题，用饱和函数sat（BT˙x，ε）来近似［19］，并定义

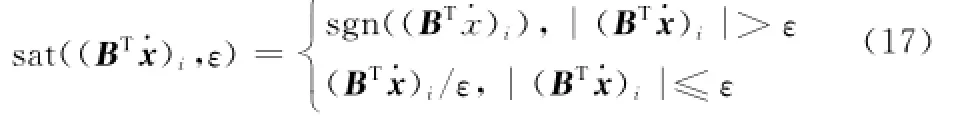
式中，（BT˙x）i（i＝1，2，3）为BT˙x的各个分量；ε＞0为边界层厚度。由于饱和函数近似符号函数带来的误差，系统不再是渐近稳定，而是渐近有界的。

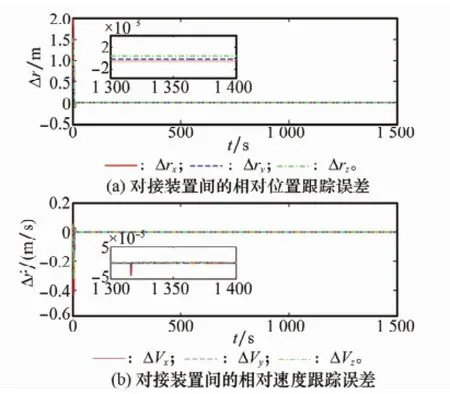
图4 对接装置间的相对位置状态跟踪误差（OTXTYTZT）

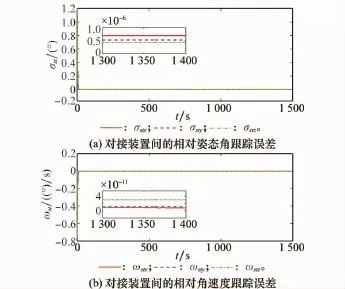
图5 对接装置间的相对姿态状态跟踪误差（ObsXbsYbsZbs）

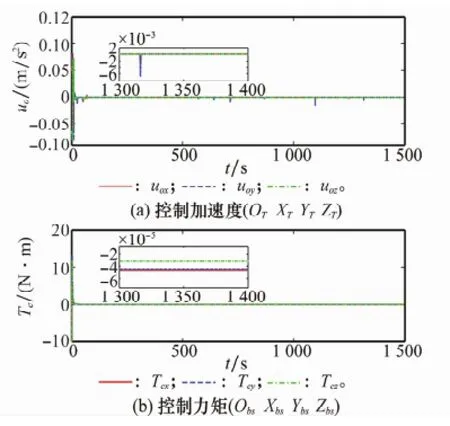
图6 服务航天器的控制加速度和力矩

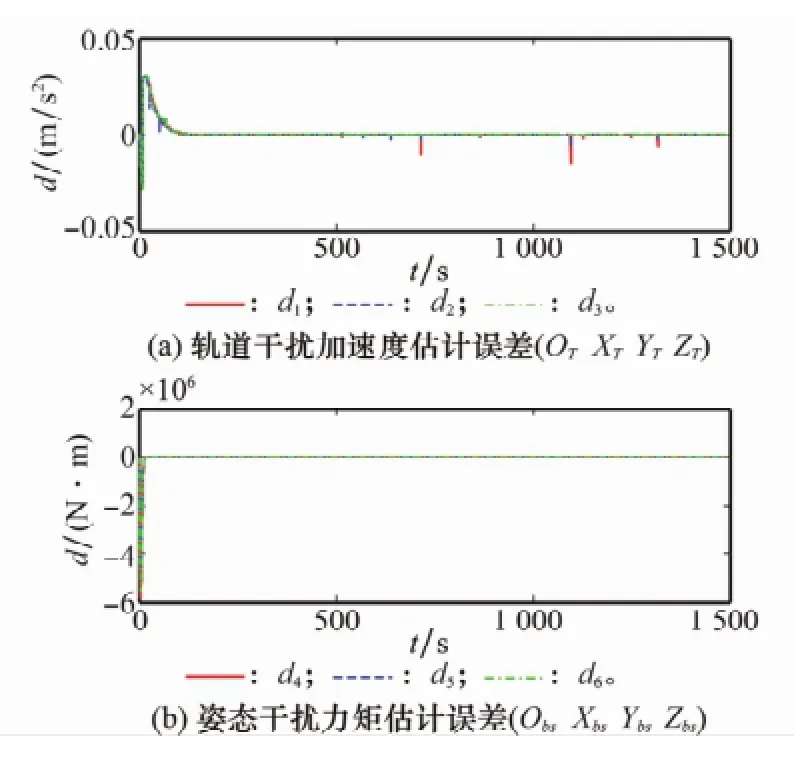
图7 干扰估计误差

由图3可见，在期望相对位置矢量ld导引下，服务航天器从目标后方150 m处沿着被动对接端口方向以0．1 m／s的速度接近，经1 500 s平稳逼近到目标被动对接端口。由图4可以看出，经过60 s左右服务航天器对接装置跟踪上期望相对位置状态（包括位置和速度）的变化，即Δr→0和Δ˙r→0。由图5可见，经过70 s左右服务航天器跟踪上目标航天器的姿态状态（包括姿态和角速度）变化，即σst→0和ωst→0。由图6可以看出，在服务航天器实现对目标的相对位置状态和相对姿态状态跟踪之前，其控制加速度和力矩相对较大，完成跟踪后迅速减小，并以相对较小的控制加速度和力矩维持相对位置状态和相对姿态状态的跟踪。由图7的干扰估计误差可知，相对位置和姿态的干扰估值分别在80 s和85 s左右趋于干扰的真值。由于主动对接端口期望的相对位置状态受到服务航天器本身姿态及目标航天器姿态的影响以及系统干扰的影响，使其在相对位置和速度的跟踪过程中出现微误差量突变，如图4所示。

为考察航天器对接机构的安装位置误差、转动惯量的不确定性误差和其他未考虑的误差因素对所设计的相对姿态轨道耦合控制器的影响，将标称惯量阵增加15%的不确定性，将干扰放大10倍进行仿真（对接机构的安装位置误差和其他未考虑的误差等效为干扰放大），其他的仿真参数不变，结果如图8和图9所示。仿真结果显示，服务航天器相对位置状态和相对姿态状态的跟踪过程依然平稳。对比图4和图5，稳态时位置跟踪精度下降10倍，姿态跟踪精度下降103倍，表明惯量阵不确定性对姿态控制精度影响较大。但仿真结果显示所设计控制器仍然具有较高的控制精度，这说明本文所设计的控制律是有效的，并具有较好的鲁棒性。

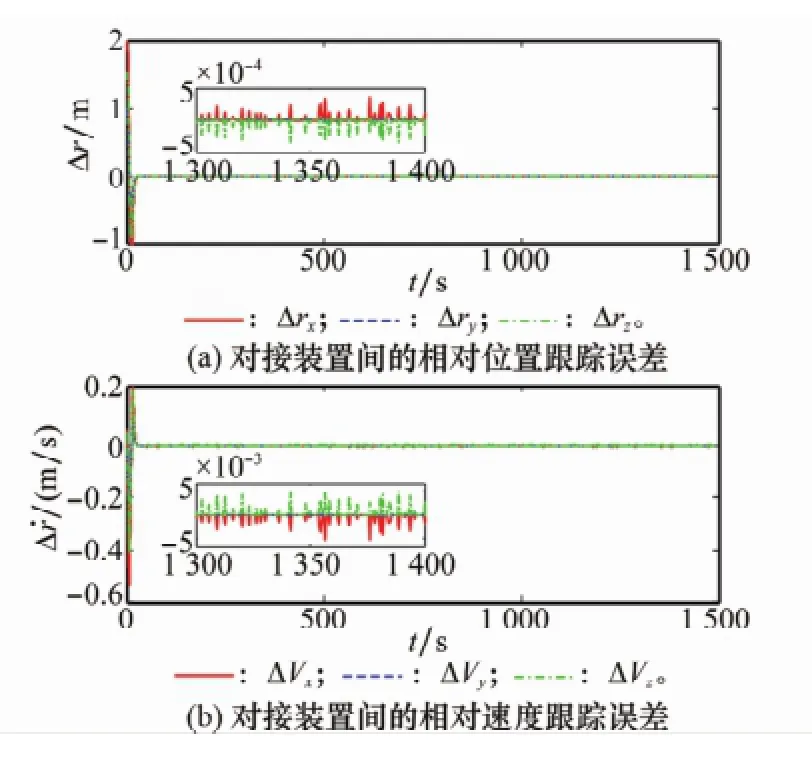
图8 干扰放大后的相对位置状态跟踪误差（OTXTYTZT）

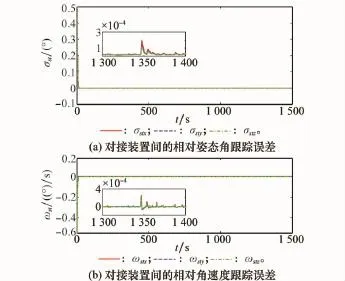
图9 干扰放大后的相对姿态状态跟踪误差（ObsXbsYbsZbs）

4 结论

服务航天器超近程逼近目标至对接的过程中相对姿态和轨道是耦合的。本文建立了考虑对接装置安装位置的相对姿轨一体化耦合动力学模型。通过引入描述相对运动构型变化的期望相对位置矢量和位置误差矢量，将相对轨道跟踪控制问题转化为调节器设计问题。考虑了相对姿轨耦合性及未知干扰影响，设计了相对姿轨耦合控制律。仿真中考虑控制输入受限，仿真结果表明本文所设计的控制算法是有效的，并具有较好的控制性能，且对外界干扰具有一定的鲁棒性。本文提出的通过设计期望相对位置矢量来描述相对运动构型变化的方法，同样适用于其他空间操作的控制实现，如航天器的空间快速绕飞及编队飞行队形保持等。

［1］Long A，Richards M，Hastings D E．On-orbit servicing：a new value proposition for satellite design and operation［J］．Journal of Spacecraft and Rockets，2007，44（4）：964- 976．

［2］Lu W，Geng Y H，Chen X Q，et al．Coupled control of relative position and attitude for on-orbit servicing spacecraft with respect to target［J］．Acta Aeronautica et Astronautica Sinica，2011，32（5）：857- 865．（卢伟，耿云海，陈雪芹，等．在轨服务航天器对目标的相对位置和姿态耦合控制［J］．航空学报，2011，32（5）：857- 865．）

［3］Okasha M，Newman B．Guidance，navigation and control for satellite proximity operations using Tschauner-Hempel equations［C］∥Proc. of the AIAA Guidance，Navigation，and Control Conference and Exhibit，2011．

［4］De Q M S，Kapila V，Yan Q G．Adaptive nonlinear control of multiple spacecraft formation flying［J］．Journal of Guidance，Control and Dynamics，2000，23（3）：385- 390．

［5］Pan H Z，Kapila V．Adaptive nonlinear control for spacecraft formation flying with coupled translational and attitude dynamics［C］∥Proc.of the 40th IEEE Conference on Decision and Control，2001：2057- 2062．

［6］Song S M，Zhang B Q，Chen X L．Robust control of spacecraft attitude tracking for space fly-around mission［J］．Systems Engineering and Electronics，2011，33（1）：121- 124．（宋申民，张保群，陈兴林．空间绕飞任务中航天器姿态跟踪的鲁棒控制［J］．系统工程与电子技术，2011，33（1）：121- 124．）

［7］Zhu Z B，Li G，He Y Z，et al．Cooperative relative attitude and translation control based on finite horizon optimization and differential Theta-D method［J］．Journal of Astronautics，2012，33（2）：167- 174．（朱志斌，李果，何英姿，等．基于滚动优化和微分Theta-D方法的快速绕飞航天器姿轨协同控制［J］．宇航学报，2012，33（2）：167- 174．）

［8］Singla P，Subbarao K，Junkins J L．Adaptive output feedback control for spacecraft rendezvous and docking under measurement uncertainty［J］．Journal of Guidance，Control，and Dynamics，2006，29（4）：892- 902．

［9］Lee D，Pernicka H．Optimal control for proximity operations and docking［J］．International Journal of Aeronautical&Space Science，2010，11（3）：206- 220．

［10］Subbarao K，Welsh SJ．Nonlinear control of motion synchronizations for satellite proximity operations［J］．Journal of Guidance，Control，and Dynamics，2008，31（5）：1284- 1294．

［11］Tie Y J，Yang W，Yue X K．Improving adaptive synchronization control of coupled spacecraft attitudeand orbit［J］．Journal of Northwestern Polytechnical University，2012，30（1）：32-37．（铁钰嘉，杨伟，岳晓奎．航天器姿轨耦合控制自适应同步控制［J］．西北工业大学学报，2012，30（1）：32- 37．）

［12］Xin M，Pan H J．Nonlinear optimal control of spacecraft approaching a tumbling target［J］．Aerospace Science and Technology，2011，15（2）：79- 89．

［13］Xing G Q，Parvez S A．Alternate forms of relative attitude kinematics and dynamics equations［J］．Frontier Science，2008，2（8）：53- 59．

［14］Xing G Q，Parvez S A．Relative attitude kinematics＆dynamics equations and its applications to the general spacecraft attitude state tracking control problem［J］．Frontier Science，2008，2（7）：26- 34．

［15］Xing G Q，Parvez S A．Implementation of autonomous GPS guidance and control for the spacecraft formation flying［J］．Frontier Science，2008，2（5）：59- 62．

［16］Xing G Q，Parvez S A．Design and implementation of synchronized autonomous orbit and attitude control for multiple spacecraft formation using GPS measurement feedback［J］．Frontier Science，2008，2（6）：63- 70．

［17］Lu W．Relative position and attitude coupled control for on-orbit servicing spacecraft rendezvous and docking to an out-ofcontrol target［D］．Harbin：Harbin Institute of Technology，2012．（卢伟．在轨服务航天器与失控目标交会对接的相对位姿耦合控制［D］．哈尔滨：哈尔滨工业大学，2012．）

［18］Geng Y H，Lu W，Chen X Q．Attitude synchronization control of on-orbit servicing spacecraft with respect to out-control target［J］．Journal of Harbin Institute of Technology，2011，44（1）：1- 6．（耿云海，卢伟，陈雪芹．在轨服务航天器对失控目标的姿态同步控制［J］．哈尔滨工业大学学报，2011，44（1）：1- 6．）

［19］Slotine J J．Sliding mode controller design for nonlinear system［J］．International Journal of Control，1984，40（2）：421- 434．

Coupled control of relative position and attitude for servicing spacecraft approaching the target in close proximity

ZHANG Qing-zhan，JIN Yong-qiang，KANG Zhi-yu，XIAO Yu-zhi
（Aerospace System Engineering Shanghai，Shanghai 201109，China）

Considering the relative position and attitude coupled control problem for servicing spacecraft approaching the target in close proximity，a novel coupled dynamic model is derived and an effective control law is designed．Via introducing the desired relative position vector and position error vector，which describe the relative motion configuration，the relative position tracking control is transformed to the regulator design．Considering installation location of docking mechanisms，the coupled relative position and attitude dynamic equations are derived．And considering unknown bounded interference，the coupled relative position and attitude control law is proposed by using the Lyapunov stability theory．Under the condition of bounded control inputs in numerical simulations，the results indicate that the coupled control law is effective with perfect performance．

on-orbit servicing；relative position and attitude；coupled control；dynamics；desired relative position vector

V 448．2

10．3969／j．issn．1001-506X．2015．01．23

张庆展（1987-），男，工程师，硕士，主要研究方向为航天器姿态、轨道控制。

E-mail：zh．q．zh＠163．com

靳永强（1981-），男，高级工程师，博士，主要研究方向为航天器姿态、轨道控制。

E-mail：jinyong_qiang＠126．com

康志宇（1976-），男，研究员，博士，主要研究方向为航天器总体设计。

E-mail：kzy＠126．com

肖余之（1964-），男，研究员，硕士，主要研究方向为航天器总体设计。

E-mail：xyz＠126．com

1001-506X（2015）01-0141-07