融合自忆性原理的优化GM（1，1）幂模型构建及应用

郭晓君，刘思峰，方志耕，吴利丰

（1．南通大学理学院，江苏南通226019；

2．南京航空航天大学经济与管理学院，江苏南京211106）

融合自忆性原理的优化GM（1，1）幂模型构建及应用

郭晓君1，2，刘思峰2，方志耕2，吴利丰2

（1．南通大学理学院，江苏南通226019；

2．南京航空航天大学经济与管理学院，江苏南京211106）

针对因发展变化受众多因素影响而具有饱和增长趋势或单峰特性的原始波动序列，为了提高预测精度，以灰色GM（1，1）幂模型为基础，构建了自忆性原理与优化GM（1，1）幂模型的耦合预测模型，用动力系统自忆性原理来克服传统灰色模型对初值比较敏感的弱点。结果表明，新构建模型能够充分利用系统的多个历史时次资料，模拟和预测精度都高于传统优化GM（1，1）幂模型，进一步拓展了灰色模型的应用范围。最后，以我国高中升学率的数据为例验证了所构建模型的优越性和有效性。

灰色系统；GM（1，1）幂模型；自忆性原理；升学率

0 引 言

针对系统工程中不断出现的复杂性和不确定性等特征，1982年邓聚龙［1］提出了一种新的系统科学方法——灰色系统理论，主要包括灰色关联、预测建模、决策分析、灰色控制等。其中，灰色预测模型系列［2］利用累加原始序列弱化其随机性，进而构建具有部分差分、部分微分特征的方程，挖掘数据序列的内在规律，做出科学定量的预测，用以揭示系统的未来发展趋势。同时，灰色预测模型不受一般统计模型对原始数据种种要求的约束，对样本容量和概率分布没有严格要求，在小样本时间序列预测方面具有独特优势，已在经济、能源、交通等各类动态系统中取得了广泛应用［35］。此外，众多学者也致力于对灰色预测模型的基础研究，例如分析模型特性、改进背景值、优化时间响应式等［6-8］。

GM（1，1）幂模型，作为其中一类具有较强普适性的非线性灰色模型，是对GM（1，1）模型和灰色Verhulst模型的形式衍化，其幂指数可以根据实际系统背景进行优化选取，以适用于不同规律的原始序列建模，演绎系统内蕴的非线性特征。针对早期研究选取幂指数的不合理性，王正新等学者对GM（1，1）幂模型进行了一系列深入研究［912］，其中文献［9］和文献［12］运用灰色系统信息覆盖、非线性优化等方法来寻求最优的幂指数，对于解决幂指数的优化选取难题意义深远。

基于将决定论和不确定论相结合的思想，文献［13］提出了一种新的预测技术——动力系统自忆性原理，吸收了动力学与统计学各自的优势［14］，可以对非线性系统进行有效预测。该预测方法可以充分挖掘系统内蕴的历史信息，从而反演得到相应的系统动力学模型，预测系统的整体发展及变化趋势。自忆性模型理论，是对传统初值问题数值解和统计预测方法的一个突破，已在水文气象、电力能源、建筑物沉降等领域［15-16］取得了较为理想且稳定的预测效果。

同时，自忆性技术也逐步与灰色预测方法进行了一些有意义的结合［17-18］，但文献［17］仅研究具有近似指数增长或衰减特征的GM（1，1）模型，文献［18］则以特殊的DHGM（2，2）模型为对象进行讨论，仅适用于水文系统模型。而本文考虑灰色预测模型应用的普适性，以传统的优化GM（1，1）幂模型为基础，面向近似指数增长或衰减、饱和增长或呈单峰特性的原始波动序列，结合自忆性原理，构建自忆性优化GM（1，1）幂预测模型，并以我国历年高中升学率为例进行模拟和预测，分析自忆性模型相比传统模型的优越性，以期拓展灰色预测方法、提高其应用普适性。

1 GM（1，1）幂模型及幂指数优化

1.1 原始GM（1，1）幂模型

定义1 设非负原始数据序列

对X（0）作一阶累加，得1-AGO序列

其中

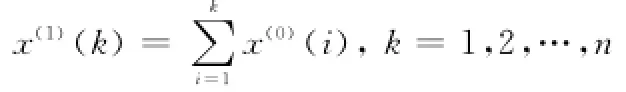
对X（1）作一阶紧邻均值，得1-MGO序列

其中

则称

为等间距GM（1，1）幂模型。

GM（1，1）幂模型中，发展系数－a、灰色作用量b，以及幂指数γ均为未知参数。特别地，当γ＝0时，GM（1，1）幂模型可退化为传统GM（1，1）模型；当γ＝2时，GM（1，1）幂模型又退化为灰色Verhulst模型。本文以等间距GM（1，1）幂模型为基础，构建融合自忆性原理的优化GM（1，1）幂模型，非等间距GM（1，1）幂模型的情况可进一步拓展推导得到。

定义2［7］设参数a，b如定义1所述，则称

为等间距GM（1，1）幂模型的白化微分方程。

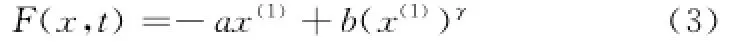
1.2 GM（1，1）幂模型的求解过程

设X（0）为非负原始数据序列，且X（0），X（1），Z（1）如上所述，则等间距GM（1，1）幂模型的求解过程可归纳如下：

步骤1 若^R＝［a，b］T为参数列，且

则等间距GM（1，1）幂模型x（0）（k）＋az（1）（k）＝b（z（1）（k））γ的最小二乘估计参数列满足

步骤3 对式（4）作离散化处理，得GM（1，1）幂模型x（0）（k）＋az（1）（k）＝b（z（1）（k））γ的时间响应序列

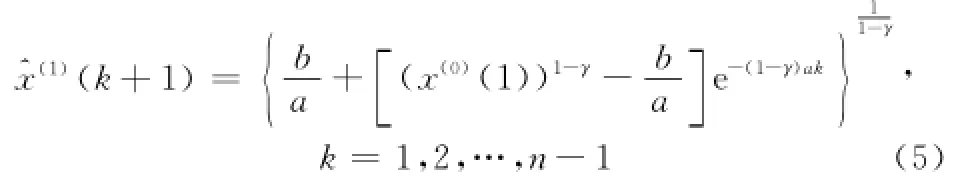
步骤4 对式（5）作一阶累减还原，得原GM（1，1）幂模型预测序列

1.3 GM（1，1）幂模型的幂指数优化

GM（1，1）幂模型是一类具有较强柔韧性和灵活性特点的非线性灰色模型，随着幂指数γ取值的不同可适用于不同特征的原始序列建模。早期文献中，幂指数γ往往通过主观判断或建模实验来取值，势必影响了灰色幂模型的普适性。幂指数γ通常取值为2，即灰色Verhulst模型，也仅适用于具有饱和状态趋势的原始序列建模预测。因此，如何根据不同原始数据内蕴的演化规律，借助优化算法工具来确定幂指数γ的最优值在建模过程中显得尤为重要。

文献［9］利用灰色系统信息覆盖的思想提出了一种确定幂指数γ的优化算法，即

式中

同时对幂指数γ在不同取值范围内，GM（1，1）幂模型解可能产生的性质影响作了进一步讨论。

2 融合自忆性原理的优化GM（1，1）幂模型

2.1 动力系统自忆性原理的基础理论

从混沌动力学可知，系统兼有决定论和随机性两方面特性，故而随机-动力途径是研究系统发展变化的基本思路。基于系统演变的不可逆特性，自忆性原理通过重点研究系统内部的前后状态，来挖掘系统自身的演化趋势。文献［13］将记忆函数代入Hilbert空间，利用内积运算导出自忆性差分-积分方程，该方程可以充分挖掘出历史数据中蕴含的系统信息。由于系统自忆性方程以多个时点初值条件来代替单个时点初值条件，从而克服了原始系统动力微分方程对初值比较敏感的弱点，因此这种自忆性技术同时吸收了动力学与统计学两方面的预测优势。

式中，x为变量；λ为参数；t为时间；F（x，λ，t）为动力核。

式（8）表达了变量x在局地的时间变化与动力核源函数F（x，λ，t）的关系，令记忆函数为β（t），且|β（t）|≤1，同时在Hilbert空间中定义内积

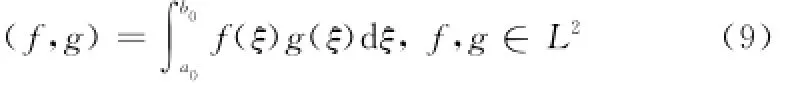
2.2 自忆性优化GM（1，1）幂模型的构建步骤

等间距自忆性优化GM（1，1）幂模型的建模过程可归纳如下：

步骤1 优化选取幂指数γ

根据文献［9］，利用灰色系统信息覆盖的思想选取符合不同原始数据序列特征的最优幂指数γ，即

步骤2推导自忆性差分-积分方程

设某时间集合T＝｛t－p，t－p＋1，…，t－1，t0，t｝，各时次间隔为Δt，其中当前时刻以t0表示，历史时刻以t－p，t－p＋1，…，t－1，t0表示，预测时刻以t表示，回溯时点数以p表示，称为回溯阶。若假设变量x与记忆函数β（t）具有连续性、可微性、可积性，则原始系统动力方程式（8）可借助内积运算式（9）变换为

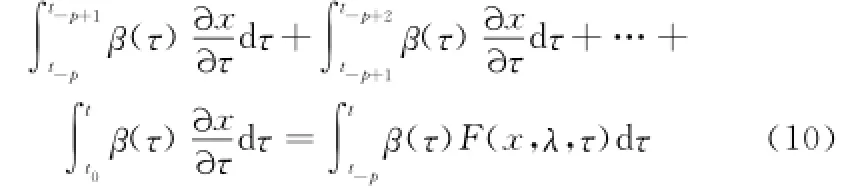
式（10）可以视为以β（t）为权重的一种加权积分，经过分部积分及积分中值公式处理，并作同类项约减，式（10）转化成一个差分-积分方程，即自忆性预测方程

式中，βt≡β（t）；xt≡x（t）；βi≡β（ti）；xi≡x（ti）；中值xmi≡x（tm）；ti＜tm＜ti＋1；i＝－p，－p＋1，…，0。

步骤3 离散化自忆性预测方程

令xm－p－1≡x－p，β－p－1≡0，式（11）可变换为

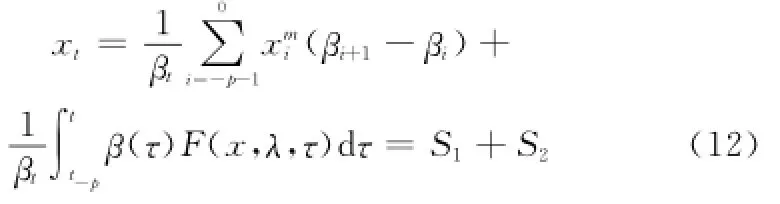
称其为系统回溯p阶的自忆性方程，强调了系统状态前后时次间的联系。其中，S1为自忆部分，强调p＋1个时次的历史统计数据对预测值xt的影响；S2则为他效部分，强调动力核F（x，λ，t）在时间段［t－p，t0］内对xt的回溯影响。

在式（12）中，将积分运算近似为求和运算，微分运算近似为差分运算，中值xmi则近似为两相邻时刻值，即

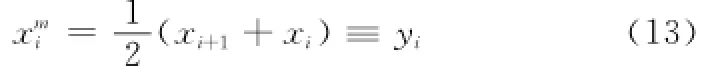
同时取等距时次间隔，令Δti＝ti＋1－ti＝1，且将βt和βi合写，则得到离散形式的自忆性预测方程则离散形式的自忆性预测方程式（14）可表示成矩阵形式

式中，记忆系数为αi＝（βi＋1－βi）／βt和θi＝βi／βt，原始等间距GM（1，1）幂模型可确定函数F（x，λ，t），即－ax（1）＋b（x（1））γ。

步骤4 最小二乘求解记忆系数

F（x，λ，t）视为系统的输入，x视为系统的输出，自忆性方程可借助递推最小二乘、随机近似、遗传算法等方法来求解，本文考虑最小二乘法。假设有L（L＞p）个时点的原始数据序列，记

从而得记忆系数矩阵W的最小二乘估计

步骤5 求解自忆性预测模型

利用记忆系数αi和θi，便可求解自忆性预测方程式（14），得到相应的模拟或预测值x＾（1）（t），进而通过一阶累减还原，可得原始数据模拟预测序列

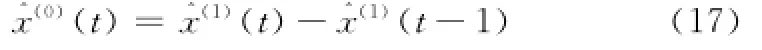
式中，t＝1，2，…，n，且x＾（1）（0）≡0。可以借助Matlab程序减轻运用自忆性预测方程进行模拟和预测时的计算工作量。

步骤6 检验模拟预测精度

将k时点的相对误差记为RPE（k），即

可由k时点相对误差RPE（k）及系统平均相对误差ARPE来检验自忆性优化GM（1，1）幂模型模拟和预测的精度并进行误差分析。

将所有时点的平均相对误差记为ARPE，则

3 应用实例

为了验证本文提出的融合自忆性原理优化GM（1，1）幂模型的可行性，以及面向具有饱和增长趋势或单峰特性的原始波动序列模拟和预测的优越性，以文献［10］中1990～2008年的中国高中升学率为研究对象进行建模分析，相关统计数据如表1所示。考虑到我国1999年实施的扩招政策对高中升学率增长产生的影响，为了消除国家政策等扰动因素的影响，以1999年为临界点划分为1990～1998年和1999～2008年前后两段序列，进行分段建模预测。由于两段升学率序列分别呈现先增长后下降的单峰特性，考虑用GM（1，1）幂模型对其进行分段建模分析。

表1 1990～2008年中国高中升学率%

本文将自忆性成份融入传统的GM（1，1）幂模型，构建一类自忆性优化GM（1，1）幂模型，利用其对历史统计数据充分记忆的优势，来预测中国高中升学率的发展趋势及变动情况。同时，通过对比新模型与传统优化GM（1，1）幂模型［9］的单点及平均模拟预测精度，来分析新模型中自忆性成份所体现的预测优势及稳定性，从而拓展其应用领域及普适性。

3.1 第一阶段建模分析

取1990～1998年的统计数据作为建模样本，首先根据幂指数优化算法的计算公式（7）可得最优幂指数γ＝0.523 6，同时根据统计数据建立第一阶段传统优化GM（1，1）幂模型的白化微分方程

x＾（1）（k＋1）＝（27.738 0－22.905 3 e－0.0935k）2.0991

再将式（20）的右端项作为自忆性方程的动力核F（x，λ，t），则有d x／d t＝F（x，λ，t），据此可建立中国高中升学率的自忆性优化GM（1，1）幂一阶段预测模型，其中回溯阶经试算确定p＝1为最优，则相应自忆性离散预测方程为

其中，记忆系数矩阵为

利用文献［9］中的传统优化GM（1，1）幂模型和上述构建的自忆性优化GM（1，1）幂模型，进行建模预测和误差后验的结果见表2，新建模型中初始两个时点因回溯阶p＝1而没有模拟值。

表2 第一阶段（1990～1998年）两种模型的模拟值与误差对比

中国高中升学率第一阶段（1990～1998年）的建模分析及误差对比结果如表2所示，传统模型中8个样本单点相对误差介于1．26%与8．75%之间，平均相对误差为3．50%；而新建模型中的7个样本单点相对误差借助自忆性技术大幅降低，介于0．06%与2．41%之间，且平均相对误差也显著减少至1．04%。同时，图1描绘出了两种GM（1，1）幂模型模拟值的相对误差分布对比情况，显然可见新模型的单点相对误差显著低于传统模型，且总体分布较为稳定。

图1 两种GM（1，1）幂模型模拟值的相对误差分布对比（1992～1998年）

3.2 第二阶段建模分析

针对1999～2008年的中国高中升学率，取前8年的统计数据作为建模样本，同时取后两年的统计数据作为预测样本，进行预测检验。同理，根据幂指数优化算法公式（7）可计算得最优幂指数γ＝－0.019 9，同时根据统计数据建立第二阶段传统优化GM（1，1）幂模型的白化微分方程

再将式（22）的右端项作为自忆性方程的动力核F（x，λ，t），则有＝F（x，λ，t），据此可建立中国高中升学率的自忆性优化GM（1，1）幂二阶段预测模型，其中回溯阶经试算确定p＝1为最优，从而得到自忆性离散预测方程

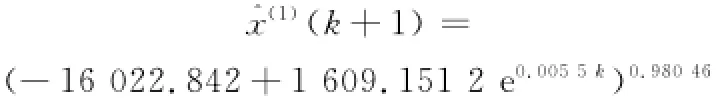
其中，记忆系数矩阵为

利用文献［9］中的传统优化GM（1，1）幂模型和上述构建的自忆性优化GM（1，1）幂模型，进行建模预测和误差后验，结果见表3，同样新建模型中初始两个时点因回溯阶p＝1而没有模拟值。

中国高中升学率第二阶段（1999～2008年）的建模分析及误差对比结果如表3所示，传统模型中7个样本单点相对误差介于0.08%～8．40%，平均相对误差为4．75%；而新建模型中的6个样本单点相对误差借助自忆性技术大幅降低，介于0%～2．61%，且平均相对误差也显著减少至1．18%。在预测方面，自忆性优化GM（1，1）幂模型的优势更加明显，单步滚动预测相对误差仅为2．31%，远低于传统优化GM（1，1）幂模型的10．64%，而两步滚动预测相对误差虽然伴随预测步长有所增加，但仍显著低于传统模型的9．63%。同时，图2描绘出了两种GM（1，1）幂模型模拟值和预测值的相对误差分布对比情况，显然可见新模型的单点相对误差显著低于传统模型，且总体误差分布较为稳定。

表3 第二阶段（1999～2008年）两种模型的模拟值、预测值与误差对比

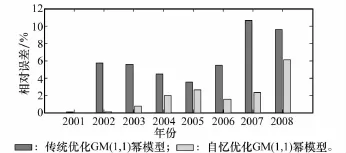
图2 两种GM（1，1）幂模型模拟值和预测值的相对误差分布对比（2001～2008年）

由中国高中升学率的建模分析结果可知，融合自忆性成份的优化GM（1，1）幂模型，利用自忆性离散预测方程包含多个初值条件的优势，克服了传统GM（1，1）幂模型受单个初值条件局限的弱点，从而显著提高了建模精度及预测可靠性。因此，新建的自忆性优化GM（1，1）幂模型，可以深入挖掘系统中所呈现的整体单峰特性及个别波动情形，更加紧密捕捉了动态系统的整体演化趋势和个体变动情况。

4 结 论

作为GM（1，1）模型和灰色Verhulst模型的衍生，GM（1，1）幂模型是一类具有较强普适性的非线性灰色模型，其幂指数的优化取值反映了该模型的柔韧性和灵活性。本文将自忆性成份有机融入传统的优化GM（1，1）幂模型，利用其对历史统计数据充分记忆的优势，构建了一类自忆性优化GM（1，1）幂预测模型。对中国高中升学率的实例研究结果表明，所提出的新预测模型能够充分挖掘系统的历史统计信息，相比传统模型具有优越的预测性能，值得推广应用于其他类似的非线性系统。

自忆性优化GM（1，1）幂模型有着广阔的研究背景和应用空间，如何借助非线性规划等优化方法进行回溯阶寻优，需要作进一步探索。同时，可以考虑如何将其他优化技术与自忆性原理相结合，进一步提高系统预测的精度和稳定性。

［1］Deng J L．Control problem of grey system［J］．Systemsand Control Letters，1982，1（5）：288- 294．

［2］Liu S F，Lin Y．Grey systems theory and applications［M］．Berlin：Springer-Verlag，2010：107- 148．

［3］Wu L F，Liu S F，Wang Y N．Grey Lotka-Volterra model and its application［J］．Technological Forecasting&Social Change，2012，79（9）：1720- 1730.

［4］Li D C，Chang C J，Chen C C，et al．Forecasting short-term electricity consumption using the adaptive grey-based approachan Asian case［J］．Omega，2012，40（6）：767- 773．

［5］Guo H，Xiao X P，Forrest J．A research on a comprehensive adaptive grey prediction model CAGM（1，N）［J］．Applied Mathematics and Computation，2013，225（1）：216- 227.

［6］Cui J，Liu S F，Zeng B，et al．Parameters characteristics of grey Verhulst prediction model under multiple transformation［J］．Control and Decision，2013，28（4）：605- 608．（崔杰，刘思峰，曾波，等．灰色Verhulst预测模型的数乘特性［J］．控制与决策，2013，28（4）：605- 608．）

［7］Zhang B，Xi G Q．GM（1，1）model optimization based on the background value and boundary value correction［J］．Systems Engineering-Theory&Practice，2013，33（3）：682- 688．（张斌，西桂权．基于背景值和边值修正的GM（1，1）模型优化［J］．系统工程理论与实践，2013，33（3）：682- 688．）

［8］Dang Y G，Liu S F．The GM models that x（n）be taken as initial value［J］．The International Journal of Systems&Cyberntics，2004，33（2）：247- 254.

［9］Wang Z X，Dang Y G，Liu S F，et al．Solution of GM（1，1）power model and its properties［J］．Systems Engineering and Electronics，2009，31（10）：2380- 2383．（王正新，党耀国，刘思峰，等．GM（1，1）幂模型求解方法及其解的性质［J］．系统工程与电子技术，2009，31（10）：2380- 2383．）

［10］Wang Z X，Dang Y G，Li X M．On whitening the grey parameters of grey power model［J］．The Journal of Grey System，2011，23（3）：223- 228．

［11］Wang Z X，Dang Y G，Lian Z W．Unbiased GM（1，1）power model and its application［J］．Chinese Journal of Management Science，2011，19（4）：144- 151．（王正新，党耀国，练郑伟．无偏GM（1，1）幂模型及其应用［J］．中国管理科学，2011，19（4）：144- 151．）

［12］Wang Z X，Dang Y G，Zhao J J．Optimized GM（1，1）power model and its application［J］．Systems Engineering-Theory& Practice，2012，32（9）：1973- 1978．（王正新，党耀国，赵洁珏．优化的GM（1，1）幂模型及其应用［J］．系统工程理论与实践，2012，32（9）：1973- 1978．）

［13］Cao H X．Self-memory equation for atmosphere motion［J］．Science in China（Series B）：Chemistry，1993，36（7）：845- 855.

［14］Phienwej N，Thepparak S，Giao P H．Prediction of differential settlement of buildings induced by land subsidence from deep well pumping［J］．Geotechnical Engineering，2005，36（1）：69- 75.

［15］Gu X Q，You X T，Zhu H，et al．Numerical tests of efficiency of the retrospective time integration scheme in the self-memory model［J］．Progress in Natural Science，2004，14（9）：833- 836．

［16］Wang W，Su J Y，Hou B W，et al．Dynamic prediction of building subsidence deformation with data-based mechanistic self-memory model［J］．Chinese Science Bulletin，2012，57（26）：3430- 3435．

［17］Fan X H，Zhang Y．A novel self-memory grey model［J］．Systems Engineering-Theory&Practice，2003，23（8）：114- 117，129．（范习辉，张焰．灰色自记忆模型及应用［J］．系统工程理论与实践，2003，23（8）：114- 117，129．）

［18］Chen X D，Xia J，Xu Q．Differential hydrological grey model（DHGM）with self-memory function and its application to flood forecasting［J］．Science in China（Series E）：Technological Sciences，2009，52（4）：1039- 1049．

Construction and application of optimized GM（1，1）power model incorporating self-memory principle

GUO Xiao-jun1，2，LIU Si-feng2，FANG Zhi-geng2，WU Li-feng2
（1.School of Science，Nantong University，Nantong 226019，China；2.College of Economics and Management，Nanjing University of Aeronautics and Astronautics，Nanjing 211106，China）

As for the fluctuating sequences characterized by saturated condition or single-peak，whose development and variation are subject to multi-faceted factors，the coupling prediction model combining the selfmemory principle and the optimized GM（1，1）power model has been constructed based on the grey GM（1，1）power model in order to improve prediction accuracy．The traditional grey model’s weakness as being sensitive to the initial value can been overcomed by the self-memory principle of dynamic system．The results indicate that the newly-established model can take full advantage of the systematic multi-time historical data．It extends the grey model’s application span，which possesses higher accuracy of simulation and forecast than the traditional optimized GM（1，1）power model．Finally，the superiority and effectiveness of this proposed model have been proved by the case of Chinese senior high school students’enrolment rate into higher education institutions．

grey system；GM（1，1）power model；self-memory principle；enrolment rate

N 941．5

A

10．3969／j．issn．1001-506X．2015．01．19

郭晓君（1978-），男，讲师，博士研究生，主要研究方向为灰色系统理论、系统工程。

E-mail：guoxj159＠163．com

刘思峰（1955-），男，教授，博士研究生导师，博士，主要研究方向为灰色系统理论、数量经济学。

E-mail：sfliu＠nuaa．edu．cn

方志耕（1962-），男，教授，博士研究生导师，博士，主要研究方向为管理科学与工程、系统工程。

E-mail：zhigengfang＠163．com

吴利丰（1983-），男，博士研究生，主要研究方向为灰色系统理论、系统工程。

E-mail：wlf6666＠126．com

1001-506X（2015）01-0117-06

网址：www．sys-ele．com

2014- 03- 12；

2014- 05- 21；网络优先出版日期：2014- 08- 20。

网络优先出版地址：http：／／w ww．cnki．net／kcms／detail／11．2422．TN．20140820．1730．001．html

欧盟第7研究框架玛丽·居里国际人才引进计划Fellow项目（FP7-PIIF-GA-2013- 629051）；国家自然科学基金（71111130211，71171113，71363046，71401051）；国家社会科学基金重点项目（12AZD102）；国家社会科学基金重大招标项目（10＆ZD014）；江苏省普通高校研究生科研创新计划项目（CXZZ13_0184）；南通市科技计划项目（HS2013026，BK2014030）；南京航空航天大学引进人才基金（1009-YAH14003）资助课题