基于效能评估的空中对抗作战建模分析

2015-06-19陈长兴牛德智唐冬丽

系统工程与电子技术 2015年1期

关键词：蓝方数据链空战

陈长兴，牛德智，王卓，符辉，唐冬丽，陈强

（1．空军工程大学理学院，陕西西安710051；2．空军工程大学防空反导学院，陕西西安710051）

基于效能评估的空中对抗作战建模分析

陈长兴1，牛德智1，王卓1，符辉1，唐冬丽2，陈强1

（1．空军工程大学理学院，陕西西安710051；2．空军工程大学防空反导学院，陕西西安710051）

针对效能评估与作战运用未能有效衔接的问题，研究了空中对抗作战中的兵力变化问题。给出了数据链体制下作战飞机效能评估计算方法，通过函数映射法将评估结果转化为平均战斗力水平，证明了二者的等价性和一致性。以蓝彻斯特方程为基础，建立了空中兵力变化的数学模型和有增援情况时的空战模型。将用微分方程描述的模型离散化，指出了离散时间步长所应满足的约束条件，形成了完整的模型求解数值计算方法。仿真实验结果表明，数据链可以改变双方作战实力，提高作战能力，增援作战时选择“局部最优增援时刻点”可以获得更高的增援效率。

效能评估；数据链；数值计算；蓝彻斯特方程；决策

0 引言

武器系统的效能评估问题，不仅可以为装备生产研制过程中提供合理的费效分析，而且可以为衡量武器的整体作战能力提供量化的参考依据［1-4］。航空武器系统装备数据链终端，是信息化联合作战的必然要求。近几场局部战争表明，数据链具有独特的战场态势共享、精确指挥控制和武器协同的无缝链接优势，已经越来越成为武器装备的生命线［5-6］。美军从20世纪50年代开始研制数据链并先后将各种不同类型数据链运用到作战飞机上，其空中作战能力大幅度提高［7-8］。对装备数据链系统的作战飞机，进行科学合理的效能评估，并将结果运用到作战实践中，完成航空作战体系循环的全过程［9-12］，是一个急需完成的科学命题。

在现有关于数据链和作战效能评估的研究中，一些典型成果如：文献［13］用一种新方法研究了飞机作战中的效能评估问题，研究结果仅限于给出不同对象的效能大小；文献［14］讨论了数据链支持下的空战双方飞机数量的变化问题，分析具有一定的合理性，但是模型中缺少一个直接反映数据链作用的量化指标，这样不利于直接研究数据链对空战双方格局的影响；文献［15］引入了战场感知系数并将其运用到蓝彻斯特方程中进行作战分析，这对于考虑空战兵力的变化融入了信息因素，但对模型中的作战效能未进行相关研究。

本文出发点就是给出一种数据链体制下的飞机效能评估方法，并将结果运用到空战对抗的数学建模中，实现评估与作战的一体化。

1 单机作战的平均战斗力水平

1.1 基于数据链的效能评估方法

数据链下的飞机效能评估思路是：从分析数据链的功能，找到其对效能评估的影响因素，进而通过用解析法描述的效能评估模型给出综合效能值。效能评估的方法较多，如典型的ADC法、AHP法等［3］，本文是要选取一种能清晰描述数据链对飞机效能影响的方法，数据链对飞机效能及空战的影响定量体现。ADC法用概率量来描述不同指标，但该法难以有效描述出数据链的关联作用，如有效度中的可靠性、可信赖度中的安全性、能力中的精度等都与数据链相关，但是这种相关不易模型化体现。AHP法将整个飞机系统按照目标层、准则层、方案层来逐级划分，建立层级指标体系来进行效能评估，该法虽可把数据链的作用考虑进去，但存在权值赋予具有一定的主观性，指标量化也会因方法而异。所以，本文采用对数法来描述飞机效能，据此考虑数据链下的新效能。当然，对数法也有不足之处，此处不再做重点讨论。对数法中，飞机的空战能力指数可表示为［16- 17］

式中，I为空战能力指数；C表示机动性；D表示火力；E表示探测目标能力；ε1～ε4分别表示生存力、电子对抗能力、航程和飞行员操纵效能系数。

由于具有态势共享优势，数据链使得超视距打击成为可能。另外，数据链在传感器、指控单元和武器平台之间实时传输战术信息，可以遂行发现即打击的任务，实现了从传感器到射手的无缝链接。分析数据链的这些作用及对应对数法模型中的参数可知，探测目标和电子干扰能力会在数据链作用下得到提高，这样，数据链环境下的空战能力可以表示为

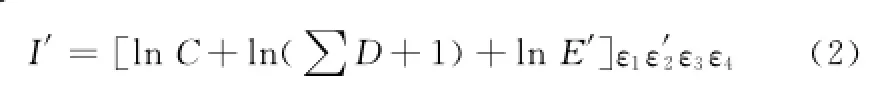
式中，E′和ε′2分别表示使用数据链后的探测和电子对抗能力，且E′＝E＋λ1E，ε′2＝ε2＋λ2ε2，λ1和λ2表示数据链对这两项参数的提升率。

对于λ1的确定，需要根据不同作战模式和数据链体制有所不同，这里仅考虑一种简单的双机协同作战时数据链对探测能力提升率的计算方式。假定双机为同向直线飞行的情况，则提升率可以用探测面积的变化比来表示：

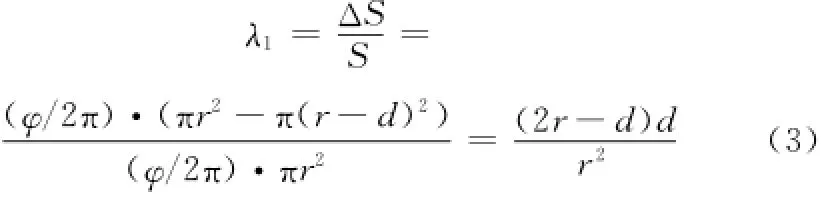
式中，φ为雷达搜索的方位角；r为雷达探测距离；d为双机之间距离（d＜r）。

对于λ2的确定，可以在现有处理方法基础上对其统一赋值研究。文献［16］给出了机载电子电子对抗设备的电子对抗能力，全向雷达告警系统为1.05，全向雷达告警＋消极干扰投放＋导弹逼近警告系统的综合系统为1.16～1.20，有数据链支撑下的电子对抗设备，还会增加积极干扰投放功能，所以对其赋值时可以使其适当大于无数据链支持下的电子对抗能力。

1.2 空战能力指数转化为平均战斗力水平

由式（1）及文献研究的结果知，空战能力指数一般远大于1。在空战中，考虑单机一次战斗只打击一架敌机的情况，则应该用单机的平均战斗力水平来衡量杀伤效率或作战威力。

作如下变换：

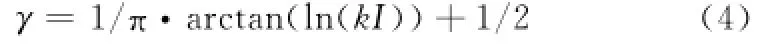
将I变换到在区间（0，1）上的平均战斗力水平γ（其中k＞0，作用是避免γ在数值上过于集中）。为此证明γ和I是等价的。

证明令A＝｛x|x∈Z，x＞0｝，B＝｛x|x∈Z，0＜x＜1｝，作一映射f：A→B，有

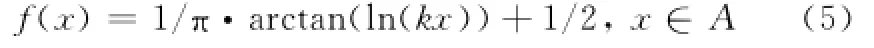
因为x∈A，则ln（kx）∈（－∞，＋∞）。且arctan（ln（kx））∈（－π／2，π／2），所以1／π·arctan（ln（kx））∈（－1／2，1／2）。即有1／π·arctan（ln（kx））＋1／2∈（0，1）。

说明f∶A→B是由A到B的一一映射，这样A和B是等势（等价）的，即A～B。

又

因为x＞0，k＞0，所以f′（x）＞0。且f（x）为增函数，即在式（4）中，γ随I的增大而增大，随γ的减小而减小，二者变化关系一致。证毕

2 空战中的兵力变化建模

2.1 蓝彻斯特方程分析方法

在对作战兵力变化规律的研究中，本文以蓝彻斯特方程为基础，并分析不同作战场景下的动态兵力变化过程。此处给出蓝彻斯特方程（平方律）的表达式为

式中，R，B为红、蓝方数量；t为时间；α，β为蓝、红方每个战斗单位的平均战斗力水平。其求解可通过式（1）～式（4）来具体确定。

对式（7）求解微分方程组的状态解为

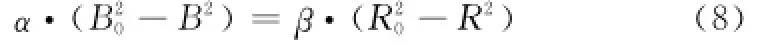
令x＝1－R／R0表示红方兵力的消耗率，y＝B／B0表示蓝方兵力的剩余率。L＝β·R20／α·B20表示红蓝双方的战斗实力比，L＞1时表示红方战斗实力强，L＜1时表示蓝方战斗实力强，L＝1时双方实力相等。将x，y，L代入式（8），得

式（9）描述了在双方实力比L约束下的消耗率与剩余率之间关系，在L确定的情况下，可以分析出战斗结局。

2.2 数据链体制下的空中力量对抗建模

考虑在数据链情况下的空战模型。首先求解平均战斗力水平的提升率ηR和ηB，即有ηR＝（γR′－γR）／γR，ηB＝（γ′B－γB）／γB。

在空战过程中，综合性能更优的数据链一方拥有更大优势，不仅可以实施更加积极主动的电子干扰，而且可以在有目标来袭时在更远距离上发出预警提示等，这样，定义一数据链水平占优因子为

则数据链体制下的空战兵力变化规律建模为

从式（10）中可知，η实质是个可正可负的量，为正时对红方有增进作用，反之对蓝方。

类似式（7）～式（9）的分析可得

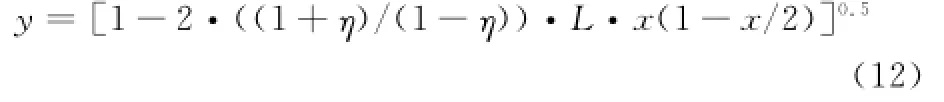
式中，（1＋η）／（1－η））·L定义为等效实力比。

另外，考虑有增援时的模型为

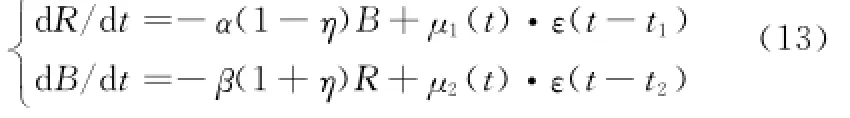
式中，μ1（t），μ2（t）分别为双方的增援率（可以恒定，也可以变化）；t1，t2为增援开始时刻；ε（t）为阶跃函数，用来限制增援兵力加入时间。

2.3 模型的数值计算方法

用微分方程组描述的数学模型，意义比较明确，体系也比较完整，但是微分方程组的求解一般比较困难。若在式（13）的基础上在综合考虑别的因素（如非战斗减员等），空战对抗模型将更加复杂，虽然在某些情况下可以借助特定软件求解，但是模型中各变量的变化规律及内在的影响关系不易分析和掌握。所以，需要将微分方程组描述的数学模型离散化，研究其数值计算方法。

首先讨论最基本的蓝彻斯特方程，由微分方程的定义入手，可以将式（7）中的第1个方程（第2个方程的分析方法类似）离散化为

式中，Δt为一个一定小的时间步长，在该时间步长的Δt下，可以基本保持原微分方程的变量变化规律。在离散取值时，依次令t＝0，Δt，2Δt，…，nΔt（考虑在一场空战中，它是由若干个战斗波次构成的，而每个战斗波次又可以细分为一定数量的战斗回合，则此处的n可以理解为总的战斗回合数），且将RnΔt简记为Rn，则式（14）可化为

在数值计算时，需要确定Δt取多大的时间步长才合适，文献［15］中将蓝彻斯特方程直接转化为差分方程形式，其实质是直接令Δt＝1，这样处理不仅会失去建立在微分方程基础上的作战模型中变量的变化规律（主要是与Δt足够小的要求相违背），而且所得的计算数据太过片面性，对研究作战规律不利。为此，写出式（15）的完整形式为

将式（16）中方程组的左右两边分别相加，得到

当蓝方最后失败时，有Bn－1为0（或近似为0），且可以将Bn－1的变化近似用等差数列来描述，则式（17）化为

进一步，可以求出

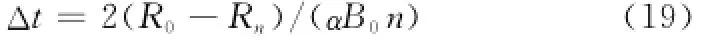
由式（8）可知，令B＝0，可以得到

至此，得到了离散取样间隔与战斗回合数（或描述战斗兵力变化的细分过程数）之间的关系，在数值计算（包括式（11）和式（13））时，可以取时间间隔小于或者等于式（18）中的时间间隔，从而研究战斗中的双方兵力变化过程。类似地，若采用式（7）中的第2个方程进行讨论，考虑最终失败的为红方，则时间间隔可取为

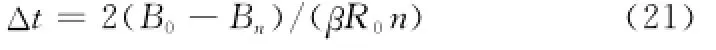
这样，数据链体制下的空战兵力变化离散模型可以表述为

式中，m1，m2＝0，1，2，…为正整数，表示某一增援时刻。在战斗结束时（n＝N），红方（假定为获胜方）共增援的飞机数可以表示为Rs＝μ1·Δt·（N－nm1＋1），共损失的飞机数可以表示为Rd＝R0＋Rs－RN。

3 仿真算例

假定在空中对抗作战中，红、蓝方所用分别为米格-29和F-15E机型。仿真中假定仅红方有数据链支持。米格-29的雷达型号为NO-9，其最大探测距离为90 km，这样协同作战距离为70 km时，根据式（3）可求λ1＝0.95。设定红、蓝方的电子对抗能力分别为1.05和1.2，红方使用数据链后子对抗能力变为1.8。评估指标中的其余参数参照文献［17］，将飞机效能的每项参数列表显示并求解I（k取1／10）和γ如表1所示。

表1 飞机作战效能指标及效能评估值

从表中可以看出，数据链的引入对空战能力指数和平均战斗力水平都有所提升。

3.1 战斗实力比对空战结局的影响

取L＝［0.6，0.8，1，1.2，1.4］，仿真蓝方剩余率与红方消耗率的变化曲线如图1所示。

图1 蓝方剩余率和红方消耗率的变化关系

图1 的结果验证了第2.1节中对L不同空战结局不同的分析。

由表1中数据可知ηR＝0.21，则η＝0.21。这样在原来的L下仿真可得到剩余率与消耗率曲线（见图2）。分析图像知，在数据链情况下，当红、蓝方的实力比介于0.6～0.8之间时，双方实力平衡。令（1＋η）／（1－η））·L＝1，可求L＝0.65。这说明，采用数据链后，红方只要大于蓝方实力的65%时就可获胜，反之失败。图2中也标出了双方实力平衡的分界线。

图2 引入数据链后剩余率和消耗率的变化关系

3.2 不同的增援时刻点对空战的影响

设定R＝10，B＝15，由表1结果知，α＝0.7和β＝0.6， η＝0.21。由实力比（或等效实力比）计算知，红方整体实力仍然弱于蓝方，这样实验中仅假定红方有增援（首先考虑nm1＝0的情况）且增援率为2.5。通过式（15）～式（22），仿真4种模式（分别为原始实力下双方作战、红方仅引入数据链双方作战、红方仅拥有一定速率增援力量双方作战、红方同时拥有数据链和增援力量双方作战）下双方的动态损耗见图3。

图3 不同作战条件下的双方动态损耗图

从图3可以看出，由于红方实力较弱，原始条件下的作战结果为失败；在无数据链支持下，一定的增援速率下并不能改变最终战局（当增援率一定大时可以改变）。在数据链体制下，红方有效延长了战斗进程，这在增援力量到来的情况下最终扭转战局，获得胜利。

接下来确定红方实施增援的有效增援时间范围。令增援开始时刻m1分别为0、15和30，取离散时间步长为Δt＝0.025，仿真得到双方兵力变化的动态损耗曲线见图4。

图4 红方不同的增援起始时刻时双方的动态损耗图

由图4知，当m1＝30时，增援不能改变红方失败的结果。这说明，空战增援中存在一个时间分界点，在此之前增援，可以扭转双方战局；反之不能。经过多次仿真可以确定有效增援时刻范围为［0，28］，换算到时间范围即为［0，0.7］。

进一步，让m1在［0，28］之间取值，步进量为1，其余仿真参数不变，得到的双方动态损耗曲线见图5。

图5 有效增援时刻范围内m1变化时的双方动态损耗

当m1增大时（即增援开始时刻越晚），双方的空战进程维持时间变长，红方胜利时剩余的飞机数量越少，由于相邻时间上的飞机数量变化规律比较接近，为进一步分析增援效率的高低，图6给出了m1不同时红方共增援和损失的飞机数量变化曲线。

图6 m1值不同时的红方增援和损失飞机数量变化

分析图6可知，越在增援的后期，需增援的飞机总数越多，同时损失的飞机数量也急剧攀升，这说明增援力量越早加入战斗，越能以较少的飞机数量赢得战斗。由此产生的另外一个问题是，若增援只能在更小的一个时间范围内实施（如图6中第10～15个时刻点之间进行增援），则需要给出一个科学有效的增援时刻点选取准则。

为此，引入“损增比”的概念，表示整个战斗中单方损失的飞机数量与增援的飞机数量之比，其深层含义是增援单位数量的飞机时损失的飞机数量，可给出其定义式为

根据式（24）计算“损增比”ρ，ρ值比较小的时刻点可以作为增援时刻的选择点。图7给出了与图6对应的“损增比”变化曲线。

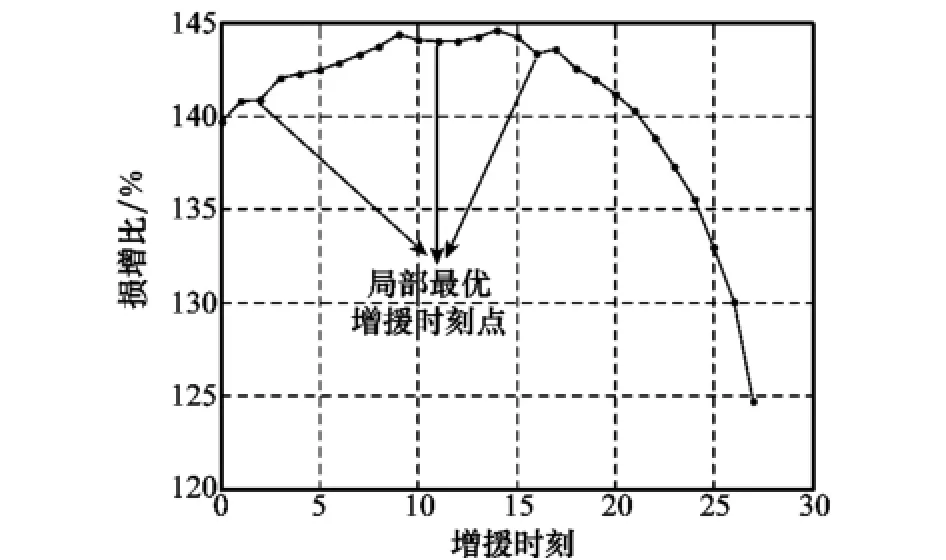
图7 不同增援时刻时的损增比曲线

从图7中可以看出，随m1值变化时，“损增比”曲线并不是简单的单调递增关系，而是存在一系列极小值点，在这些极小值点周围，损增比数值都相对较大，说明增援获得的效率并不是最高（在有效增援时间范围的末期，虽然损增比数值较小，但是其需要的增援飞机数量较多，即需要较大的增援规模才能实现，实际作战中并不一定总能满足这种规模要求）。据此可得出结论，在不同的增援时刻周围，存在使增援效率最高的局部最优点，即“局部最优增援时刻点”。掌握了该规律，便于指挥员对整场空战中在何时进行空中力量增援，以获得最高增援效率提供参考依据。

4 结论

本文对数据链体系下飞机空中对抗作战的兵力变化问题进行了研究。对数据链情形下的飞机效能评估模型进行改进，并将评估结果转化为平均战斗力水平运用到空战模型中。以蓝彻斯特方程为基础进行分析空中对抗过程中的兵力变化规律，建立了具有反映数据链效应的空中力量体系对抗数学模型和有增援时的空战模型。为更好地分析和把握空战规律，将微分方程模型离散化，给出了其数值计算方法，为仿真实现空中力量的变化过程提供了一种有效的实现途径。仿真算例说明了数据链对战斗能力的提升作用，增援时应选择“局部最优增援时刻点”以获得最大的增援效率，实验结果为运筹和指挥空战全局提供了重要参考。

［1］Yang F，Yang C C，Liang L，et al．New approach to determine common weights in DEA efficiency evaluation model［J］．Journal of Systems Engineering and Electronics，2010，21（4）：609- 615．

［2］Liu H，Xu M，Chen N Y，et al．Task effectiveness evaluation on anti-ship attack of fighter aircraft［J］．Transactions of Nanjing University of Aeronautics&Astronautics，2012，29（2）：164- 170．

［3］Yang Y L，Tai H X，Shi T．Weighting indicators of building energy efficiency assessment taking account of experts＇priority［J］．Journal of Central South University of Technology，2012，19（3）：803- 808．

［4］Gray F B，Hommedieu W．A combat-effectiveness approach to information assurance［EB／OL］．［2013- 10- 30］．http：∥enu．kz／repository／2010／AIAA- 2010- 1748．pdf．

［5］Xu Y L，Li Q Z，Xie S F，et al．Study on algorithm and communication protocol of differential GPS positioning based on pseudo range［J］．Information Technology and Application，2009，1（3）：606- 609．

［6］Tang L，Zhang R R，Chen Q B．Cross-layer design of combining AMC with H ARQ in cooperative relay system with perfect and imperfect CSI［J］．Journal of Harbin Institute of Technology（New Series），2012，19（4）：118- 128．

［7］Enel L，Guillem F．Improvements in navy data networks and tactical communication systems［J］．World Academy of Science，Engineering and Technology，2008，2（6）：97- 101．

［8］Zhou L，Zhang H Y，Wang T，et al．Static check of WS-CDL documents［C］∥Proc.of the IEEE International Symposium on Service Oriented System Engineering，2008：142- 147．

［9］Lee J，Kang S H，Rosenberger J，et al．A hybrid approach of goal programming for weapon systems selection［J］．Computers &Industrial Engineering，2010，58（3）：521- 527．

［10］Chen J，Mu Y P，Li D F．Study on effect evaluation of weapon coordinated use of fleet［J］．Military Operations Research and Systems Engineering，2009，23（3）：66- 71．

［11］Johnson I R，Mackay N J．Lanchester models and the battle of Britain［J］．Naval Research Logistics，2011，58（3）：210- 222．

［12］Yan J J，Wang Y，Wang X Y．Modeling and simulation of Lanchester equation based on game theory［C］∥P roc.of International Conference on the Business Management and Electronic Information，2011：212- 214．

［13］Xiang G D，Fu X D，Jiao L M．A method for efficiency evaluation under complex circumstance［J］．Electronics Optics&Control，2013，20（1）：19- 23．（相国栋，傅晓冬，焦利明．复杂环境下效能评估方法［J］．电光与控制，2013，20（1）：19- 23．）

［14］Xia B H，Zhou Y Y．Influence analysis of data link on modern air-air combat effectiveness［J］．Computer Engineering，2011，37（9）：257- 260．（夏白桦，周于义．数据链对现代空-空作战效能的影响分析［J］．计算机工程，2011，37（9）：257- 260．）

［15］Wu J，Yang F，Liang Y，et al．Generalized lanchester combat model for information warfare［J］．Fire Control&Command Control，2010，35（2）：50- 53．（吴俊，杨峰，梁彦，等．面向信息化战争的广义兰切斯特作战模型［J］．火力与指挥控制，2010，35（2）：50- 53．）

［16］Zhu B L，Zhu R C，Xiong X F．Aircraft effectiveness evaluation［M］．2nd ed．Beijing：Aviation Industry Press，2006．（朱宝鎏，朱荣昌，熊笑非．作战飞机效能评估［M］．2版．北京：航空工业出版社，2006．）

［17］Huang J C，Zhang Y，Yang L，et al．A quantitative evaluation method for operation efficiency of tactical data link［J］．Fire Control&Command Control，2010，35（12）：66- 69．（黄金才，张勇，杨磊，等．战术数据链作战效能定量评估方法［J］．火力与指挥控制，2010，35（12）：66- 69．）

Modeling of air combat based on effectiveness evaluation

CHEN Chang-xing1，NIU De-zhi1，WANG Zhuo1，FU Hui1，TANG Dong-li2，CHEN Qiang1
（1.College of Science，Air Force Engineering University，Xi’an 710051，China；
2.College of Air and Missile Defense，Air Force Engineering University，Xi’an 710051，China）

Aiming at aircraft effectiveness evaluation’s connection with combat application，force change problem in air combat is studied．Effectiveness evaluation computation method under data link mechanism is given，and value of effectiveness evaluation is converted to average combat level by function mapping means，which is improved to equivalent and consistent with the value．On basis of lanchester equation，mathematic model of force change in air combat is set up，including the case of being reinforced．The model described by differential equation is dispersed with a subject in discrete time internal，thus the whole numerical calculation method about solving the model is formulated．Simulation shows that data link could change combat force of each other and improve combat ability，and greater efficiency could be obtained by one’s choosing local optimum reinforcement time to join the combat．

effectiveness evaluation；data link；numerical computation；lanchester equation；decision making

TN 957．51

10．3969／j．issn．1001-506X．2015．01．14

陈长兴（1964-），男，教授，博士，主要研究方向为现代通信理论、信息系统建模、效能评估。

E-mail：xachenchangxing＠yahoo．com

牛德智（1984-），通信作者，男，博士研究生，主要研究方向为通信系统与雷达信息处理、系统工程与效能评估。

E-mail：niudezhi_001＠163．com

王卓（1984-），男，讲师，硕士，主要研究方向为信号与信息处理、作战理论与应用。

E-mail：wz93861＠163．com

符辉（1986-），男，硕士，主要研究方向为信息处理技术。

E-mail：43349291＠qq．com

唐冬丽（1987-），男，硕士，主要研究方向为测控技术。