频率源误差对地球同步轨道SAR成像性能影响分析

2015-06-19刘艳阳李真芳索志勇李锦伟

系统工程与电子技术 2015年1期

关键词：合成孔径稳定度方位

刘艳阳，李真芳，索志勇，李锦伟，保铮

（1．西安电子科技大学雷达信号处理国家重点实验室，陕西西安710071；2．上海卫星工程研究所，上海200240）

频率源误差对地球同步轨道SAR成像性能影响分析

刘艳阳1，2，李真芳1，索志勇1，李锦伟1，保铮1

（1．西安电子科技大学雷达信号处理国家重点实验室，陕西西安710071；2．上海卫星工程研究所，上海200240）

频率源相位误差作为合成孔径雷达（synthetic aperture radar，SAR）系统的一种时间去相干因素，对不同SAR系统的成像性能影响不同。对于低轨单基SAR系统，频率源相位误差通常可以忽略。而地球同步轨道（geosynchronous earth orbit，GEO）SAR系统具有更长的脉冲时延和合成孔径时间，此时频率源相位误差对成像性能的影响将不能被忽略。本文分析了频率源相位误差对GEO SAR系统成像性能的影响，并据此给出了GEO SAR系统对频率源相位特性的要求。

合成孔径雷达成像；地球同步轨道；频率源；相位误差

0 引言

地球同步轨道（geosynchronous earth orbit，GEO）卫星合成孔径雷达（synthetic aperture radar，SAR）因其重访周期短、地面覆盖范围大等优点，得到了国内外的广泛关注。GEO SAR系统在灾害监测（如地震）、电离层监测、土壤湿度监测等方面具有广阔的应用前景［1-5］。

星载SAR系统成像性能受到多种时间去相干因素的影响［3］，如大气延迟、频率源相位误差等。这些时间去相干因素将降低SAR图像的成像质量，包括造成SAR图像散焦、图像偏移以及积分／峰值旁瓣比损失等。频率源相位误差对不同SAR系统成像性能影响的程度不同。对于低轨星载SAR系统而言，频率源相位误差对单基系统的影响通常可以忽略，只有在双基模式下才考虑频率源相位同步误差对系统性能的影响［6-8］。与低轨单基SAR系统相比，GEO SAR系统轨道高度高，回波时延较大（约0．25 s）［9-10］，此时系统可视为工作于沿航向双基模式，并且系统合成孔径时间较长（可达百秒以上量级），这使得频率源相位误差的影响不能被忽略。与低轨双基SAR系统相比，GEO SAR系统利用同一频率源进行发射信号调制与接收回波的解调，此时频率源相位误差对GEO SAR的影响与双基SAR系统又有所不同。

本文系统地研究了频率源相位误差对GEO SAR成像性能的影响。文中首先介绍了频率源相位误差模型（包括确定性相位误差和相位噪声）和GEO SAR回波相位误差模型，然后分析了频率源确定性相位误差对GEO SAR成像性能的影响，利用典型频率源相位噪声参数分析了频率源随机相位误差对系统性能的影响，并据此给出了GEO SAR系统对频率源稳定度的要求。

1 频率源相位误差模型

实际频率源信号并非理想的正弦信号，存在随时间变化的相位误差

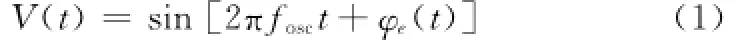
式中，fosc为频率源的理想频率；φe（t）为t时刻频率源瞬时相位误差。频率源质量通常用频率源稳定度来描述。频率稳定度按时间长短可分为长期稳定度和短期稳定度，其中长期稳定度用来描述由元器件老化以及环境条件改变引起的慢变化，短期稳定度描述的是由热噪声等因素引起的频率随机抖动变化。在实际工程应用中，通常使用一段时间内频率平均变化率［11］来描述频率源稳定度

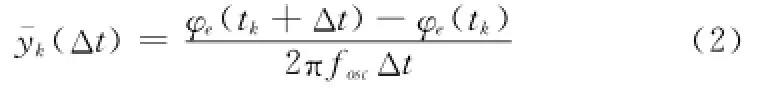
式中，Δt为时间间隔。

国内外对频率源相位误差模型进行了大量研究，这里采用文献［11］给出的频率源相位误差模型

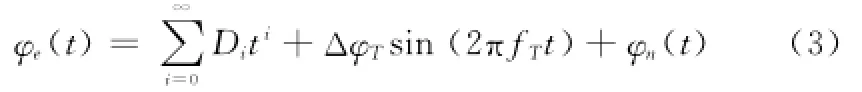
式中，Di为第i阶多项式系数；ΔφT为调制幅度；fT为调制频率。第一项为多项式模型相位误差项，第二项为周期性相位项，第三项φn（t）为频率源随机相位噪声，前两项为确定性相位误差。

通常随机相位噪声φn（t）建模为二阶平稳随机过程，在时域用Allen方差σφn（τ）描述，在频域用功率谱密度函数Sφn（f）描述。文献［11］提出的幂律模型可对常见相位噪声类型进行建模，该模型为

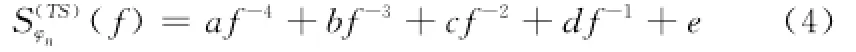
式中，a，b，c，d，e分别描述了以下噪声分量的影响：a为频率随机走动噪声；b为频率闪烁噪声；c为频率白噪声；d为相位闪烁噪声；e为相位白噪声。图1给出了星载SAR典型频率源的功率谱密度函数（幂律模型参数来自参考文献［8］，a＝－95 dB，b＝－90 dB，c＝－200 dB，d＝－130 dB，e＝－155 d B），其理想频率fosc为10 M Hz。为方便分析，下面使用相位噪声单边功率谱Sφn（f）代替（f）

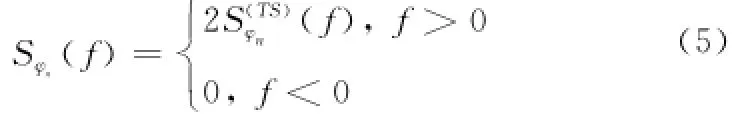
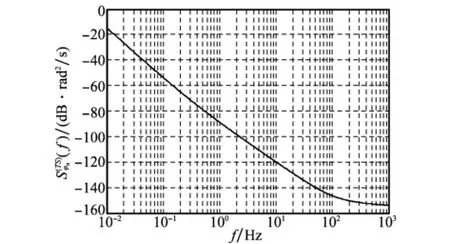
图1 星载SAR典型频率源功率谱密度函数

2 GEO SAR系统回波相位误差

GEO卫星重访周期与地球自转周期相同，卫星轨道倾角使其星下点轨迹呈“8”字型，如图2所示，其轨道根数如表1所示，图中标出了6 h和18 h时刻的星下点位置。

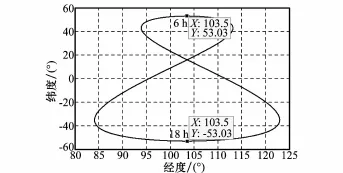
图2 GEO SAR轨道星下点轨迹

表1 GEOSAR系统典型轨道根数

GEO SAR系统卫星速度较小并且其雷达作用距离远，这使系统合成孔径时间较长。图3给出了表1所示GEO SAR卫星轨道根数下系统在一个轨道周期内合成孔径时间变化曲线。由图3可知，GEO SAR合成孔径时间较长并且随轨道位置变化，在表1所示的系统轨道根数下，其变化范围约为818～2 537 s，其最大值出现在“8”字型星下点轨迹的顶端位置，在0 h和12 h附近其合成孔径时间最短。

SAR成像处理是一个相干积累的过程，合成孔径时间内时变的相位误差将影响SAR回波信号的相干性，进而影响SAR成像质量［12-13］。GEO SAR系统成像处理时间去相干因素主要有合成孔径时间内的大气去相干、地球潮汐效应以及频率源误差等［3］。文献［3］对前两个因素进行了分析，这里将对频率源相位误差对GEO SAR成像性能的影响进行分析。

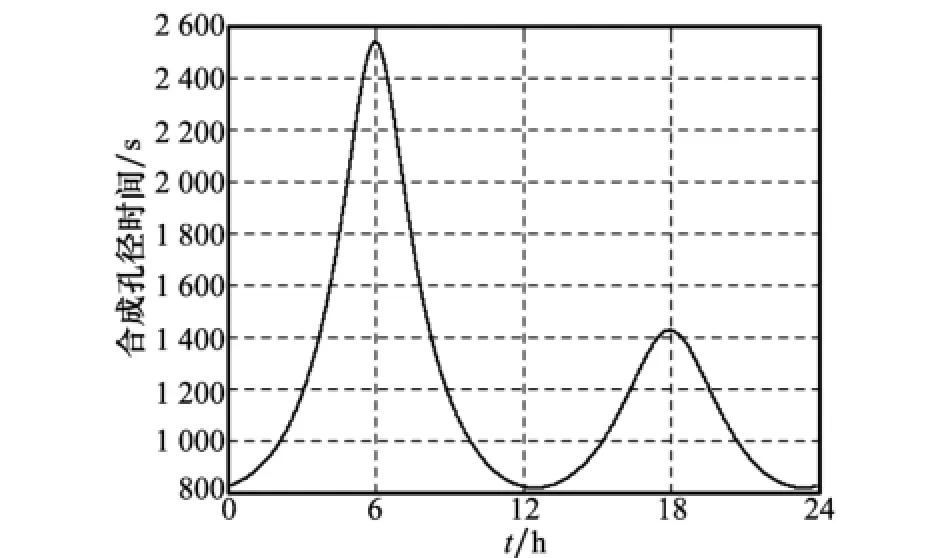
图3 GEO SAR单轨周期内合成孔径时间变化曲线

不失一般性，这里使用复信号sosc（t）表示频率源输出相位，如图4所示，频率源信号经倍频后用于发射信号的调制与接收信号的解调。经解调后，GEO SAR系统接收的视频信号可表示为

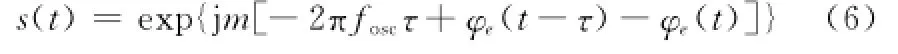
式中，m＝f0／fosc为倍频因子；f0为雷达理想载频；τ为发射信号延迟。

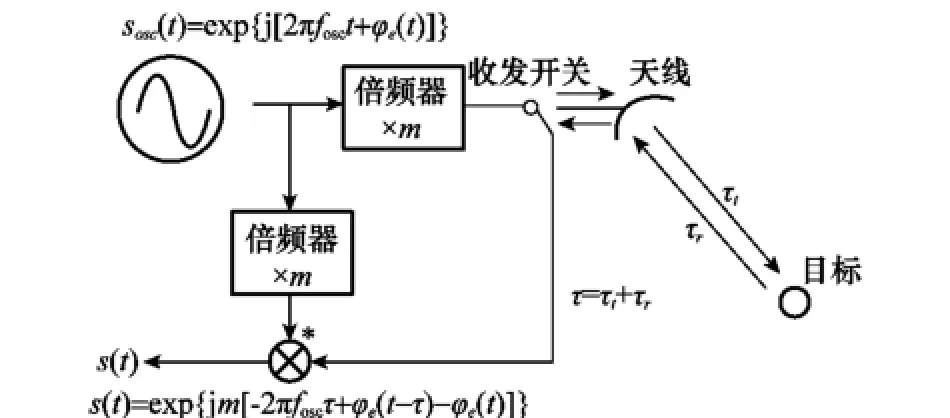
图4 GEO SAR回波相位误差模型示意图

SAR通过平台运动合成大的天线孔径以获得高分辨率SAR图像，这使得目标时延τ将随雷达的运动发生变化。SAR系统通常将时间t表示为方位慢时间tm和快时间＾t的和，即

对于方位慢时间tm发射的雷达信号，目标时延可表示为

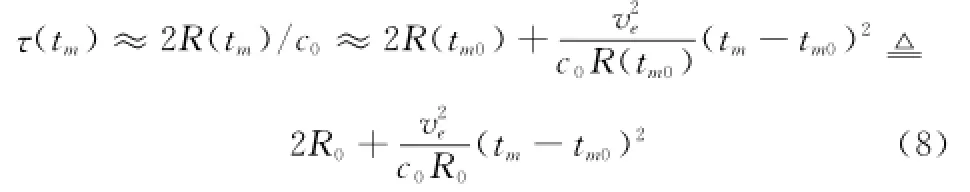
式中，R（tm）为方位时刻tm的雷达天线相位中心与目标之间的距离；c0为光速；ve为雷达等效速度［12］；R0≜R（tm0）为雷达天线相位中心与目标的最近距离，此时方位慢时间为tm0。这里需要指出的是式（8）假设了雷达信号发射与接收时刻雷达天线相位中心位置与目标的斜距近似相等，信号发射及接收期间由雷达运动引起的斜距变化量将对SAR成像性能造成一定的影响［4］，但对本文分析频率源相位误差的影响基本可以忽略。

式（6）可表示为

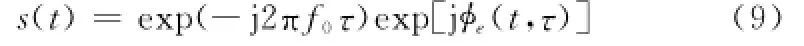
式中，φe（t，τ）＝m［φe（t－τ）－φe（t）］。式（9）中第一个指数项为理想接收信号，第二个指数项为接收信号相位误差。

3 频率源误差对GEO SAR成像性能的影响

下面分别分析确定性相位误差和随机相位误差对表2所示参数的GEOSAR系统成像性能的影响。为方便分析，下面假定GEOSAR工作在0 h附近，利用卫星状态矢量［10］可求得卫星等效速度ve≈911.6 m／s，地面波束速度vg≈323.8 m／s，合成孔径时间Ta≈818 s，雷达斜距r≈37 667 km，对应的脉冲延迟τ≈0.251 s，其方位调频率Ka≈0.183 8 Hz／s。并假定系统频率源的理想频率fosc＝10 MHz，即倍频因子m＝125。

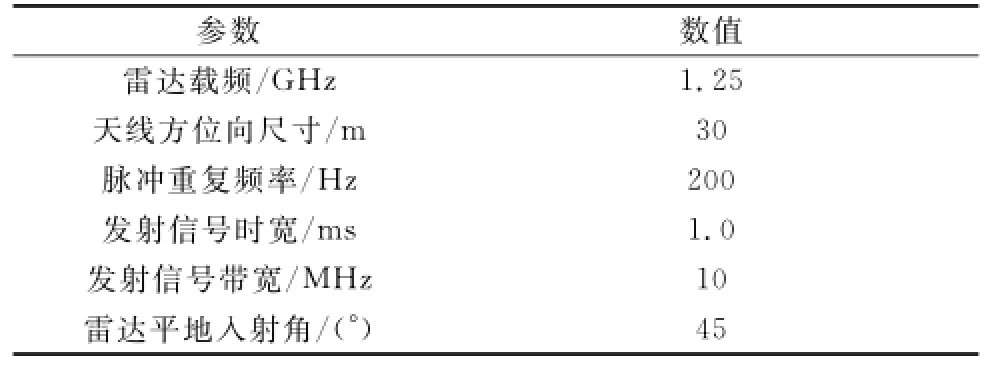
表2 GEOSAR系统典型参数

3.1 确定性相位误差

由式（2）可知，确定性相位误差包括多项式相位误差以及周期性相位误差。根据式（9），频率源初始相位误差可以对消。限于篇幅，本文忽略频率源三阶以上多项式误差对成像性能的影响，只分析三阶以下多项式相位误差以及周期性相位误差对GEO SAR系统成像性能的影响。

（1）一阶相位误差

当频率源相位误差为一阶误差模型时，即频率源频率误差为常数，此时接收信号相位误差为

该相位误差会在SAR图像中引入固定相位偏差，影响后续GEO SAR干涉处理等应用。此外，在合成孔径时间内目标延迟τ随方位慢时间tm满足二次变化规律，这将造成方位调频率误差，导致SAR图像散焦。对于低于2%的主瓣展宽，二次相位误差应控制在π／4以内［8］，此时有

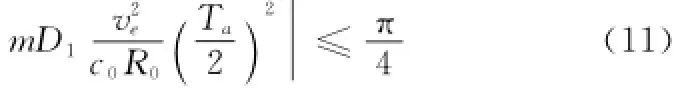
即

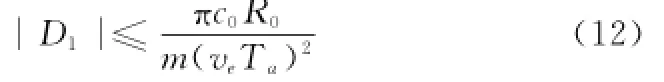
在前述系统参数下，|D1|≤510.8 Hz，此时频率源稳定度（t）≤8.12×10－6。目前典型星载SAR频率源均可满足该要求。

此外，频率源一阶相位误差还将引起SAR系统的定时误差，影响系统原始回波的数据采集，进而影响SAR图像的几何质量。

（2）二阶相位误差

当频率源相位误差为二阶模型时，即频率源频率存在

线性漂移，接收信号相位误差可表示为

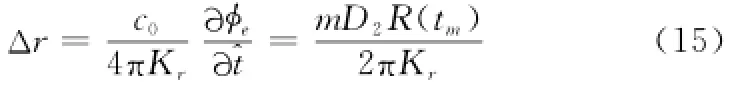
式中，第一项会引起SAR图像偏移，其中方位偏移量为

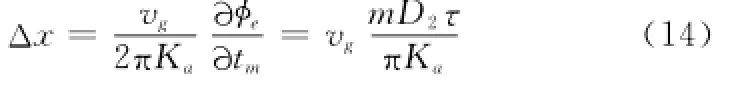
假定系统需要保证方位偏移量小于10 m，此时D2≤5.68×10－4，对应合成孔径时间内频率源稳定度y－（Ta）≤7.40×10－9。回波信号经距离压缩后，其距离向偏移量约为

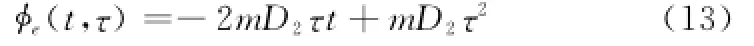
式中，Kr为发射信号调频率。在前述D2要求下，距离向偏移量Δr≤4.26×10－5m，该误差可以忽略不计。此外，当D2≤5.68×10－4时，式（13）第一项中目标延迟τ在合成孔径时间Ta内的变化引起的相位误差约为0.3°，也可忽略不计；式（13）第二项引入的相位误差约为0．25°，该相位误差也可忽略不计。

（3）三阶相位误差

当频率源相位误差为三阶相位误差模型时，接收信号相位误差为

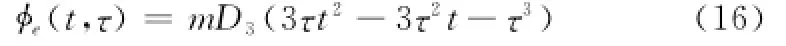
式（16）括号内第一项为随方位慢时间的二次变化量将引起方位散焦。如前所述，为保证主瓣展宽低于3%［5］，要求

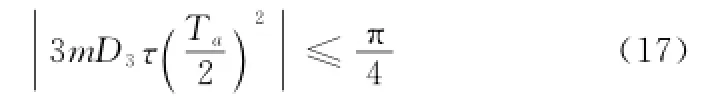
在本文仿真参数下，|D3|≤4.99×10－8，对应合成孔径时间内频率源稳定度y－（Ta）≤5.30×10－10。图5给出了频率源相位误差模型在合成孔径时间内满足三阶误差模型时点目标响应函数。由图5可知，频率源三阶相位误差不仅会造成目标分辨率降低，还将抬高目标旁瓣。式（16）括号内第一项相位误差在合成孔径时间内的变化量（时延τ引起）约为0.03°，其影响可以忽略不计。

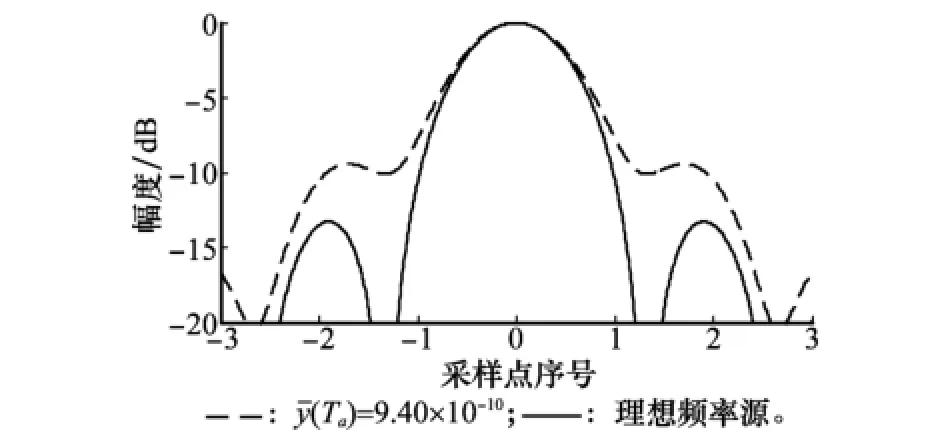
图5 GEO SAR频率源三阶相位误差模型点目标响应函数

当|D3|≤4.99×10－8时，式（16）第二项引入的方位偏移量Δx＝9.0×10－4m，可以忽略该项影响。式（16）第三项引入的相位误差约为9．87×10－8rad，该项影响也可以忽略。

（4）周期性相位误差

当频率源相位误差为周期性相位误差时，接收信号相位误差为

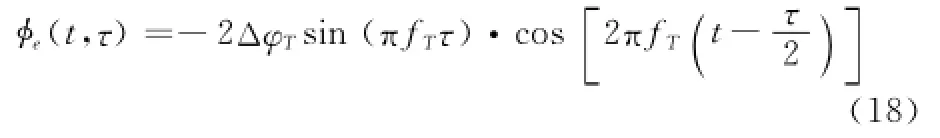
此时式（9）可写为

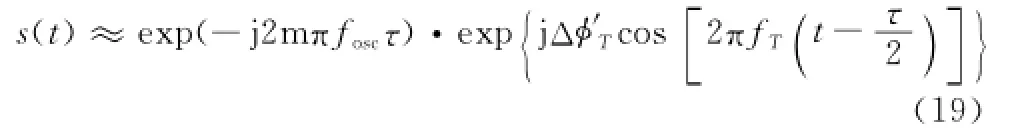
式中，Δφ′T＝－2mΔφTsin（πfTτ），通常mΔφT≪1［7］，此时接收信号可表示为

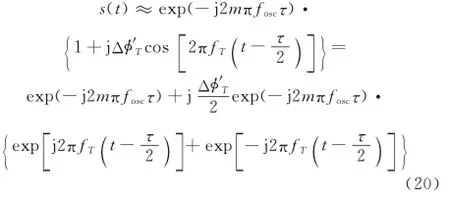
由式（20）可知，频率源正弦抖动相位误差将引起成对回波的出现［6］，成对回波将在SAR图像中引入虚假目标响应。其中，低于1／Ta的频率分量引起的虚假目标响应函数峰值将出现在真实目标的主瓣范围内，造成SAR图像主瓣展宽。而大于1／Ta的高频分量引起的目标响应函数峰值将出现在主瓣范围之外，此时虚假目标的主瓣将影响SAR图像的积分旁瓣比（integrated sidelobe ratio，ISLR）。在星载SAR系统设计时，通常要求由成对回波引起的ISLR小于－25 dB，此时有|Δφ′T|≤0.112 rad，即|ΔφTsin（πfTτ）|≤4.48×10－4rad，对应脉冲时延τ内的频率源稳定度y－（τ）≤5.70×10－11。

3.2 随机相位误差

由式（9）可知，雷达接收信号的随机相位误差φe（t，τ）的功率谱密度为

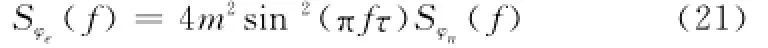
图6给出了低轨（其脉冲时延τ＝6.7 ms）和GEO SAR的随机相位噪声功率谱密度函数图，由图可知，GEO SAR低频噪声抑制能力比低轨SAR差，此时低轨SAR系统对频率源相位特性要求将不再适用于GEO SAR系统。

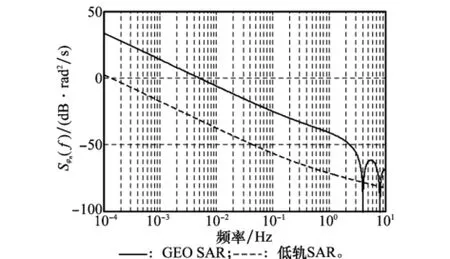
图6 高低轨SAR频率源相位噪声功率谱密度函数

频率源随机相位噪声通常会引起SAR图像偏移、主瓣展宽以及ISLR损失等影响［4－6］。下面将利用典型星载SAR系统频率源参数分析频率源误差对GEO SAR成像性能的影响。

（1）图像偏移

回波信号的线性相位误差引起SAR图像的图像偏移。对于工作于正侧视的GEO SAR系统，其回波相位误差引入的方位偏移量［7］为

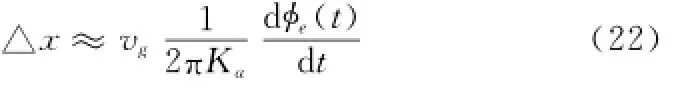
图像固定偏移可利用地面控制点加以校正，但频率源相位噪声是随机的，由相位噪声引起的图像方位偏移也将随机变化。经合成孔径相干处理后，相位噪声引起的SAR图像方位偏移量方差［8］可表示为

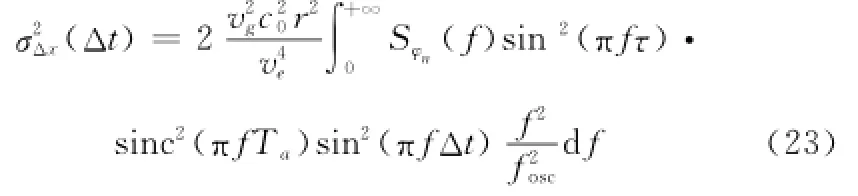
式中，Δt为目标点与校正参考点方位距离对应的时间差。图7给出了GEO SAR在图1频率源参数下方位偏移量标准差随Δt变化曲线。由图7可知，由相位噪声引起的方位偏移量相对于本系统分辨率可以忽略不计。

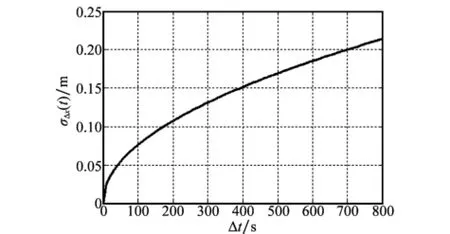
图7 GEO SAR方位偏移量标准差随Δt变化曲线

（2）主瓣展宽

SAR图像主瓣展宽主要由接收回波的二次相位误差引起。由文献［8］可知，合成孔径时间内二次相位误差的方差可通过下式进行估计：

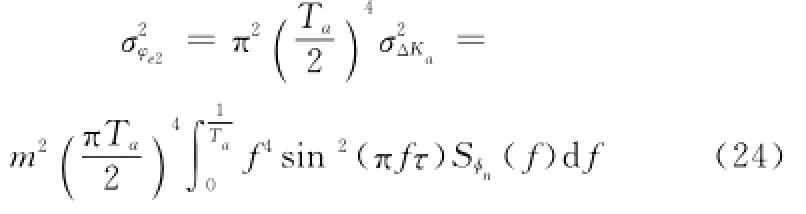
图8给出了图1所示频率源特性下频率源相位噪声引起的GEO SAR二次相位误差的标准差随合成孔径时间变化曲线。从图8中可以看出，由频率源相位噪声引起的二次相位误差的标准差约为0．1～0．18 rad，对应的方位展宽约为0．01%～0．06%。文献［8］指出由式（24）估计的二次相位误差大于真实值。因此，由频率源随机噪声引起的主瓣展宽可以忽略不计。

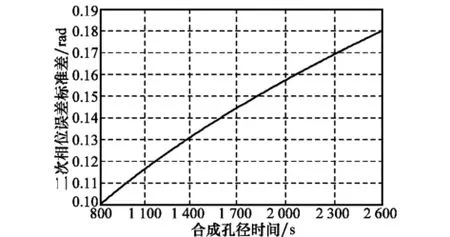
图8 GEO SAR相位噪声引起的二次相位误差的标准差随合成孔径时间的变化曲线

（3）ISLR损失

频率源相位误差将引起成对回波的出现，成对回波将在SAR图像中引入虚假目标响应。其中，低于1／Ta的频率分量主要表现为二次相位误差，由前文可知，图1所示频率源参数下二次相位误差较小，可以忽略其对ISLR的影响。但对于大于1／Ta的高频分量，由其引起的虚假目标峰值将在目标主瓣之外，此时虚假目标的主瓣将直接影响SAR图像的ISLR比。GEO SAR系统高频相位噪声对SAR图像ISLR的贡献［7－8］可表示为

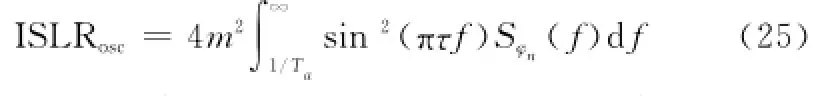
图9给出了频率源相位噪声引起的ISLR随合成孔径时间变化曲线，由图可知，当系统采用全孔径（818～2 537 s）进行成像处理时，频率源高频相位噪声引起的ISLR将高于－17 dB，并且随着合成孔径时间的增大而增大，当合成孔径时间长度为2 500 s时，ISLR将达到－12 dB。通常星载SAR系统要求频率源高频相位噪声引起的ISLR低于－25 d B，因此，系统需进一步提高频率源稳定度。此外，系统还可基于雷达回波数据在一定程度上估计高频相位误差［13］。

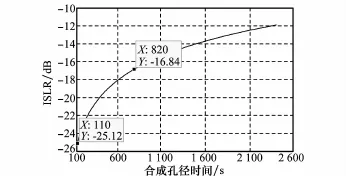
图9 GEO SAR相位噪声引起的ISLR随合成孔径时间变化曲线

4 结论

本文详细分析了频率源相位误差对GEO SAR成像质量的影响。分析结果表明：

（1）为保证GEO SAR图像质量，要求合成孔径时间Ta内的频率源稳定度y－（Ta）≤5.30×10－10，脉冲时延τ内频率源稳定度y－（τ）≤5.70×10－11。

（2）在典型星载SAR频率源相位噪声参数下，频率源随机相位误差引起的GEO SAR图像方位偏移和主瓣展宽可以忽略不计，但其对ISLR的影响较大。仿真分析结果表明，在典型频率源参数下，GEO SAR全孔径成像时频率源高频相位误差引起的ISLR将高于－17 dB。此时，系统需考虑采用更加稳定的频率源，或采用回波数据估计频率源相位误差。

本文分析研究结果对GEO SAR系统设计具有重要的理论和工程实际意义。

［1］Tomiyasu K，Pacelli J L．Synthetic aperture radar imaging from an inclined geosynchronous orbit［J］．IEEE Trans.on Geoscience and Remote Sensing，1983，21（3）：324- 329．

［2］NASA．Global earthquake satellite system：a 20-year plan to enable earthquake prediction［EB／OL］．［2012- 08- 20］．http：∥solidearth．jpl．nasa．gov／GESS／3123_GESS_Rep_2003．pdf．

［3］Bruno D，Hobbs S E．Radar imaging from geosynchronous orbit：temporal decorrelation aspects［J］．IEEE Trans.on Geoscience and Remote Sensing，2010，48（7）：2924- 2929．

［4］Hu C，Long T，Zeng T，et al．The accurate focusing and resolution analysis method in geosynchronous SAR［J］．IEEE Trans. on Geoscience and Remote Sensing，2011，49（10）：3548- 3563．

［5］Yang W F，Zhu Y，Liu F F，et al．Modified range migration algorithm in GEO SAR system［C］∥Proc.of the European Conference on SAR，2010：708- 711．

［6］Tang Z Y，Zhang S R．Influence of the frequency instability on the bistatic-SAR imaging［J］．Journal of Electronic&Information Technology，2004，26（1）：100- 106．（汤子跃，张守融．频率源稳定性对BiSAR成像的影响研究［J］．电子与信息学报，2004，26（1）：100- 106．）

［7］Xie X M，Pi Y M．Impact and estimation of frequency source noise on bistatic SAR［J］．Systems Engineering and Electronics，2010，32（2）：275- 278．（谢先明，皮亦鸣．频率源噪声对双基SAR成像的影响及评估［J］．系统工程与电子技术，2010，32（2）：275- 278．）

［8］Krieger G，Younis M．Impact of oscillator noise in bistatic and multistatic SAR［J］．IEEE Geoscience and Remote Sensing Letters，2006，3（3）：424- 428．

［9］Li J，Xing M D，Li Y C，et al．Parametric analysis and imaging method of geosynchronous SAR［J］．Systems Engineering and Electronis，2010，32（5）：931- 936．（李军，邢孟道，李亚超，等．同步轨道SAR参数分析及成像方法［J］．系统工程与电子技术，2010，32（5）：931- 936．）

［10］Tian W M，Hu C，Zeng T，et al．Several special issues in GEO SAR system［C］∥Proc.of the European Conference on SAR，2010：588- 591．

［11］Rutman J．Characterization of phase and frequency instabilities in precision frequency sources：fifteen years of progress［J］．Proceedings of the IEEE，1978，66（9）：1048- 1075．

［12］Cumming I，Wong F．Digital processing of synthetic aperture radar data：algorithm and implementation［M］．Norwood：Artech House，2005．

［13］Bao Z，Xing M D，Wang T．Radar imaging technology［M］．Beijing：Publishing House of Electronics Industry，2005：124-227．（保铮，邢孟道，王彤．雷达成像技术［M］．北京：电子工业出版社，2005：124- 227．）

Impact of frequency oscillator errors on GEO SAR imaging performance

The oscillator phase error，as one of the decorrelation factors for the synthetic aperture radar（SAR）systems，has different impacts on different SAR systems．The impacts of oscillator phase errors are negligible for the low-orbit monostatic SAR system．However，due to the long time delay of pulse return and long synthetic aperture time，the image quality of geosynchronous earth orbit（GEO）SAR suffers from the degradation caused by the oscillator phase error．The impacts of the oscillator phase error on the GEO SAR imaging performance are investigated．Furthermore，the constraints on the oscillator phase stability are given to guarantee the GEO SAR image quality．

synthetic aperture radar（SAR）imaging；geosynchronous earth orbit（GEO）；frequency oscillator；phase error

TN 957

10．3969／j．issn．1001-506X．2015．01．11

刘艳阳（1987-），男，工程师，博士，主要研究方向为星载SAR／In-SAR系统分析与信号处理。

E-mail：yanyangliu0510＠163．com

李真芳（1977-），男，教授，博士，主要研究方向为雷达成像处理。

E-mail：lzf＠xidian．edu．cn

索志勇（1979-），男，副教授，博士，主要研究方向为干涉合成孔径雷达成像处理。

E-mail：zysuo＠xidian．edu．cn

李锦伟（1987-），男，博士研究生，主要研究方向为星载InSAR系统分析与信号处理。

E-mail：ljw2006147＠sina．com

保铮（1927-），男，教授，主要研究方向为雷达信号与信息处理。