例析高考地理计算的六大命题
2015-06-18何昭
何昭





地理计算推理能力是高考要求的核心能力之一,被誉为“地理中的数学应用能力”。自地理恢复高考以来,该能力的命题方式层出不穷,从地球运动、距离计算、气温计算到人文地理中的人口增长等问题,命题方式呈现多样化趋势。跟其它地理试题相比,总体上命题难度较大,是考生最头痛的难点之一。
一、时间、昼夜长短推理计算
就近年高考试题而言,其难度已明显降低,侧重于基本规律应用,没有偏题和怪题,以中等或难度小的题目为主。而且在命题顺序上常放在前面考查,以压轴题考查的概率很小。主要考查内容:区时计算、地方时计算、经度和时间的相互计算、日出或日落的时间、昼长和夜长、昼夜长短推测月份等。
例1:(2010年新课标全国Ⅰ卷第3题)南极中山站(69°24′22″S,76°22′40″E)时间(区时)2009年2月2日9时25分,我国在南极最高点附近建立的昆仑站(80°25′01″S,77°06′58″E)正式开站。据此完成第(1)题。
(1)昆仑站正式开站时,北京时间为2009年2月2日:
A.5时25分 B.6时25分
C.12时25分 D.13时25分
解析:首先确定此题是区时计算还是地方时计算。区时根据时区计算,地方时则根据经度计算。从题中看出该题是区时计算。昆仑站位于东五区,与位于东11区的北京差3个小时且位于北京西侧,利用东加西减的方法则可得出答案。
答案:(1)C
考点链接:
☆某地时区数=该地经度÷15,余数大于7.5,所求时区为商数+1;余数小于7.5,则所求时区为商数。
☆根据各时区中央经线的地方时即为本时区区时可知相邻两个时区的区时相差1小时,即某地区区时=已知地区时±两地时区差,注意东加西减。
☆根据时间东早西晚,经度每相差15°,地方时相差1小时可求地时。即某地地方时=已知某地地方时±(两地经度差×4分钟/1°),注意东加西减。
例2:(2008年新课标全国Ⅰ卷第3~4题)图1示意不同纬度三地白昼长度变化。读图完成第(2)~(3)题。
(2)若此图表示南半球三地的白昼变化,则a、b两月分别是:
A.1月、2月 B.3月、4月
C.6月、7月 D.11月、12月
(3)在图示月份中:
A.②地夜长超过10小时
B.三地中①地昼长最长
C.三地昼长变化率在a月相等
D.三地中③地昼长变化最大
解析:第(2)题,南半球三地①②③昼长夜短,说明南半球此时为夏半年,故排除B、C选项,a、b两月比较,a月白昼长于b月,所以选A。第(3)题,在图示月份中①地昼长最短,②地昼长大于14小时,夜长小于10小时,昼长变化率①②③地越来越大,①地昼长变化最小,③地昼长变化最大。故选D。
答案:(2)A (3)D
考点链接:
☆ 某地昼长等于该地所在纬线圈昼弧度数除以15°。
☆ 日出时刻=12-昼长/2=夜长/2。
☆ 日落时刻=12+昼长/2=24-夜长/2。
☆ 极昼区昼长为24小时,极夜区昼长为0小时。
☆ 赤道上各地昼长永远是12小时。
☆ 两分日全球各地昼长均为12小时。
☆ 纬度相同地区,昼夜长短相等,日出日落时刻相同。
☆ 不同半球相同纬度的两地昼夜长短相反,即某地昼长=对应另一半球同纬度地区的夜长。
二、正午太阳高度、影长推理计算
新课标实施以来,该命题方向呈爆发趋势,如太阳方位问题、太阳高度变化、日影长短变化等。命题方式有很大转变,传统上难度较大的光照图判读已较少,无图命题较多,但难度为中等。
例3:(4)(2014年新课标Ⅰ卷第3题) 若在北回归线上建一太阳能光热电站,其高塔正午影长与塔高的比值为P,则:
A.春、秋分日,P=0 B.夏至日,P>0
C.全年日,P<1 D.冬至日,P>1
解析:在北回归线上建一太阳能光热电站,二分日时北回归线上的正午太阳高度为66.5°,影子不为0,影长与塔高比重P不等于0,A错;夏至日时,正午太阳高度为90°,影长为0,P=0,B错。冬至日,正午太阳高度为43°,影长大于塔高,P>1。
答案:(4)D
考点链接:
☆正午太阳高度计算公式:H=90°-纬度差。
纬度差指当地与太阳直射点间的纬度之差。纬度差采用“同加异减”的法则,即同半球时等于两地纬度值之差;异半球时等于两地纬度值之和。
例3中北回归线在冬至日的正午太阳高度计算过程:先计算纬度差23.5°N + 23.5°S=47°,再根据正午太阳高度计算公式可得H=90°-47°=43°。
☆日影与太阳高度的关系:日影长短取决于太阳高度;日影与太阳高度呈负相关;日影方位与太阳方位相反。
三、距离、面积推理计算
这类题重点考查学生对地图基本要素的运用能力,是地理命题的基本方向。常见计算题有根据经纬网或比例尺计算长度或面积。
例4:(2010年新课标全国Ⅰ卷第3题)南极中山站(69°22′24″S,76°22′40″E)时间(区时)2009年2月2日9时25分,我国在南极最高点附近建立的昆仑站(80°25′01″S,77°06′58″E)正式开站。
(5)昆仑站与中山站的直线距离约为:
A.820千米 B.1 020千米 C.1 220千米 D.1 420千米
解析:将昆仑站与中山站近似认为在同一条经线上,两站纬度差接近11°,故两站直线距离约为同一经线上的两点长度计算。
答案:(5)C
考点链接:
☆经线上,跨纬度1°的弧长约111km。
☆赤道上,跨经度1°的弧长约111km;任一纬线上,跨经度1°的弧长约111km×cos α(α为该地纬度)。
利用经纬网计算距离时尽量将两点放到大致同一条经线上,利用上述第一条规律计算。若没有办法放在同一经线上,看能否放到大致同一纬线上,利用上述第二条规律计算。既不在同一经线上,也不在同一纬线上,就只能利用勾股定理计算,但难度较大,2005年全国Ⅰ卷出现过。一般地图中的距离计算根据比例尺即可。
例5:(2008年全国Ⅱ卷第2题)读图2,完成第(6)题。
(6)海拔低于400米的区域面积约为:
A.0.05km2 B.0.5km2 C.5km2 D.50km2
解析:读图可知,海拔低于400米的区域位于图中东北侧,结合比例尺可量算该区域东西宽约300米,南北长约450米,由此计算出该区域面积约0.135 km2,而实际区域面积要小于0.135 km2。
答案:(6)A
考点链接:
☆求面积常用填补法,即将所算不规则区域填补成近似的长方形或正方形等较规则图形,便于计算。
☆在一般地图中,比例尺=图上距离/实地距离,所以比例尺的平方等于图幅面积与实际面积之比。
四、高差推理计算
该类高考计算题出现频率较高,只要涉及到等高线判读,往往存在高差计算。关键是正确判定等高差的数值和等高线的条数,把握好最高点和最低点的取值范围。
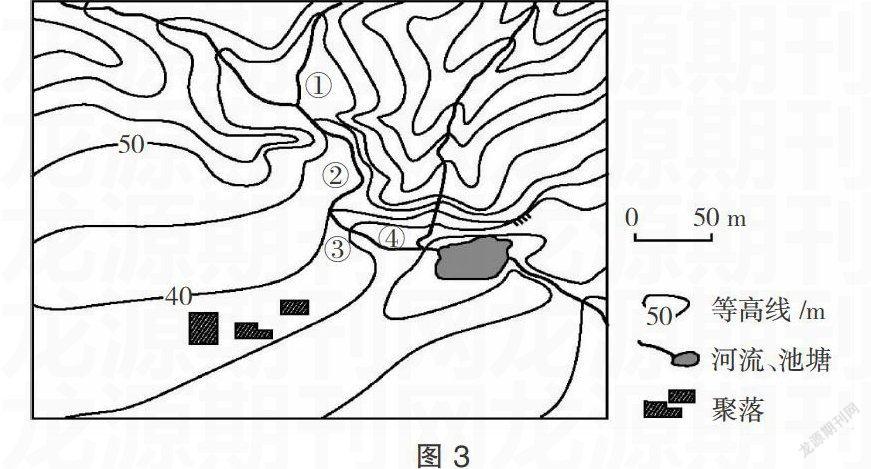
例6:(2011年新课标全国Ⅰ卷第6题)读图3,回答第(7)题。
(7)图示区域内最大高差可能为:
A.50m B.55m C.60m D.65m
解析:根据图中等高线的海拔可以推算,图中右上角(东北部)海拔最高,大于80 m,小于85 m;图中右下角(东南部)海拔最低,大于20 m,小于25 m。据此可知,图示区域内最大高差大于55 m,小于65 m。高差用对角线相减法,最大值=85-20=65,最小值=80-25=55。所以,高差在55m 答案:(7)C 考点链接: ☆高差常用对角线相减法,这是最实用的方法。高差的数值不能取最高值和最低值,只能取中间值。 ☆在计算高差中还有一种特殊情况即陡崖的计算,套用公式(n-1)d≤Δh<(n+1)d(其中n表示两地间不同等高线的条数,d表示等高距),陡崖的高差数值可以取最小值,但不能取最大值。 五、温度推理计算 常见试题有某区域的温差计算和某一高度的温度计算,这类题主要以等温线或等高线为背景进行命题,实质上是等值线的判读问题。求温差和求高差的方法一样,利用对角线相减法即可。某地的气温还要考虑天气、纬度、洋流等影响因素。 例7:(2010年大纲全国Ⅰ卷第6、8题)自某城市市中心向南、北分别设若干站点,监测城市气温的时空分布。监测时间为8日(多云)9时到9日(晴)18时,监测结果如图4所示。据此完成第(8)~(9)题。 (8)图示最大温差可能是: A.4℃ B.12℃ C.16℃ D.18℃ (9)下列时间中热岛效应最强的是: A.8日15时左右 B.8日22时左右 C. 9日15时左右 D.9日18时左右 解析:第(8)题主要考查读图判断分析问题的能力。图示地区中两条相邻等温线的温度差为2℃;通过仔细观察图示区域,9日6时左右市中心北部6千米附近温度最低5~7℃,9日15时左右市中心附近温度最高21~23℃,所以最大温差取值为14~18℃,C选项正确。第(9)题中的热岛效应取决于城区与郊区的温差,温差越大,热岛效应越明显。由图可知8日22时市中心与郊区的温差最大,热岛效应最强。 答案:(8)C (9)B 考点链接: ☆ 等温线的判读、温差计算。 ☆ 热岛效应原理。 例8:(2009年大纲全国Ⅱ卷第7题)图5中H地恰与某高压天气系统中心吻合,该天气系统以每天约200千米的速度东移。据此完成第(10)题。 (10)上午10时,H地气温为12℃,甲聚落气温为17℃。到15时甲聚落气温最接近: A.15℃ B.18℃ C.21℃ D.24℃ 解析:本题有一定难度,需综合考虑高度、天气对气温的影响。两地高差约为1 500米,按照正常的气温垂直递减率(6 ℃/1 000 m)计算两地温差是9 ℃。上午10时,当H地气温为12 ℃时,甲聚落的气温理论上应为21 ℃,但实际气温只有17 ℃,说明甲聚落此时可能正经历阴雨天气。到15时,两地气温都随着太阳辐射和地面辐射的日变化而升高,而且高压中心东移至甲聚落附近,天气转晴,气温升高,实际气温一定要高于10时的理论气温21 ℃。 答案:(10)D 考点链接: ☆温度随高度变化的两个规律:对流层气温垂直递减率为每上升100m,气温下降0.6℃; 焚风效应气温垂直递增率,每下沉100m,气温增加1℃。 六、人口问题推理计算 人口计算问题是近几年的命题方向,侧重推理较多。这种试题往往提供大量数据,利用人口自然增长三率、迁入量、迁出量等指标考查学生的推理和计算能力。2014年新课标全国Ⅰ卷出现一组人口计算的试题。 例9:(2014年新课标全国Ⅰ卷第10~11题)图6显示某国移民人数及其占总人口比例的变化。读图6,完成第(11)~(12)题。 (11)图7所示的①②③④四幅图中,符合该国人口增长特征的是: A.① B.② C.③ D.④ (12)该国人口自然增长数量最多的时段为: A.1910—1930年 B.1930—1950年 C.1950—1970年 D.1970—1990年 解析:第(11)题,结合公式:移民占总人口的比例=移民总量/人口总量,从图中适当选择几个点可以计算该地区的人口总量变化,进一步判断①图较符合。第(12)题,统计数据显示,1910年前后移民占全国人口比重较大;在1970年前后移民数量虽然下降,但变化不大,而移民占总人口比重却出现明显下降,该变化说明该时段人口自然增长快,人口总量增加最多。 答案:(11)A (12)C 考点链接: ☆某地区或国家的人口数量增长为自然增长和机械增长之和。 ☆人口数量和人口增长率是两个不同概念,人口数量=人口基数×增长率。增长率为正值则人口会增加,反之会减少。
