如何提升数学的教学效果
2015-06-17邵娟
邵娟
摘 要:解读了积极性在数学教学中的作用,尔后通过上课场景的设计诠释了学生学习积极性的培养。点滴教学经验,商榷同仁,敬请匡误斧正。
关键词:数学;教学效果;积极性;上课场景;函数
一、想方设法提高学生的积极性
面对数学当中提出的新观念“几何直观”,我们可以通过几何的观点去看待。面对这种新鲜的解决数学难题的方法,我们会发现许多难题可以通过教学得到解决。在做证明的时候,我们以往的方式是通过文字的思维去做出分析、做出判断。现在我们有了“几何直观”的新观念,可以通过圆规直尺更加清晰地画出图形来进行分析。这样我们在见证几何难题的时候,能更好地得到几何难题的答案来。让我们通过几何画图的方式,对几何难题能做出更好的预判。几何图形可以让我们更好地直接预算出结果来,让我们在图画中明白这道难题的最终结果。这在以前,我们是想象不到的。以前面对一个几何难题的时候,我们都是运用公式去见证,通过函数的公式去进行分析、去进行解决,现在我们有了“几何直观”画图的概念,就能更好地解决几何中的难题。在实际运用当中,我们可以通过数学当中的几何图形更好地去分析难题,更好地得到最终的预判结果。面对“几何直观”的新概念,我们应该在实际的解决数学难题当中去见证。有了数学“几何直观”来解决数学难题,教师可以通过最生动的图画就能让数学中的几何难题得到解决,而学生也能在几何难题中更加直观地知道难题的解决方式。这样学生在数学教学中更加有兴趣,教师也能更好地在课堂中讲学。学生的积极性提高了,教师上的数学几何题也生动有趣了。
二、设计数学上课场景
学习对称图形,针对“几何直观意识和能力的培养”设计上课场景。
1.题目类型
对称图形章节重点和难点知识,结合对称点求两点间最短距离。
2.做题技巧
配合图形,用作图引出解题思路,形成解题答案。
3.方法优点
便于理解,达到一次理解,长时间不忘,并能灵活运用。
4.题目
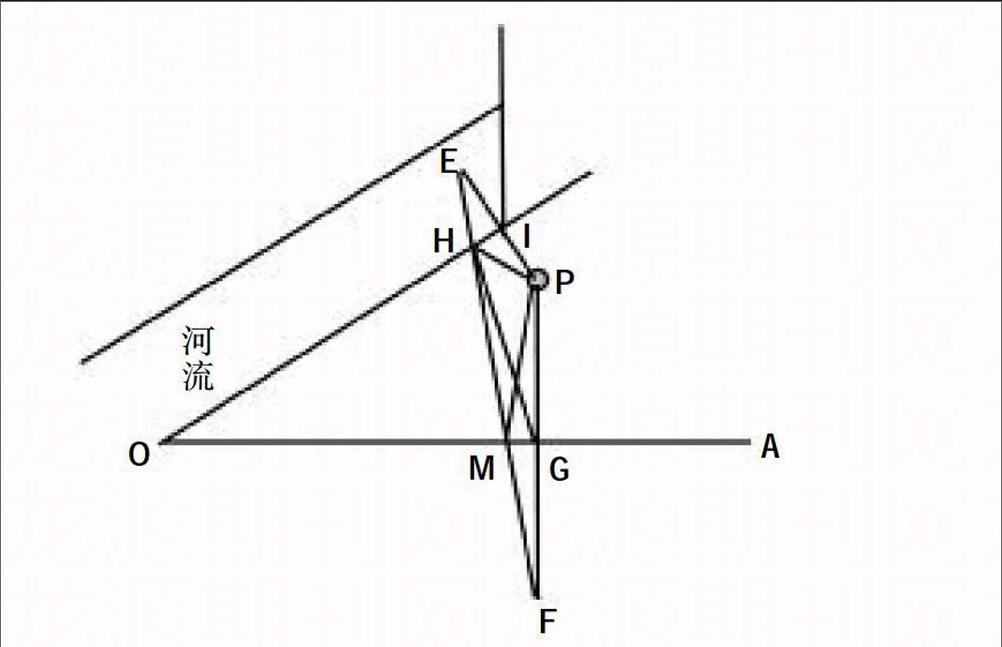
如下图,一个人从点P出发,到条形草地OA处让马吃草,然后到河流OB处让马喝水,最后回到点P处,他该怎么走行程才能最短?
■
5.解题分析
这类题型通过作图、看图更能直观得到解题思路和解题办法。
6.解题过程
同学们,要找到从点P到OA再到OB后回到点P的最短路径,我们作图如上:
如图,分别做出点P以OA、OB为对称轴的对称点F、E,并交OA、OB于点G、I,连接FE交OA、OB于点M、H。连接PM和PH,则最短路径从点P到点M再到点H最后回到点P,即:PM+MH+HP。
7.原因分析
由对称点性质得MF=MP,HE=HP,则可以将马要走的路径△PMH展开为一条直线EF。由两点间直线距离最短得到直线EF为最短距离。
8.疑问分析
同学们是不是要提出疑问了,不是点到直线间距离,垂线段距离最短吗?那最短距离应该是PG+GI+IP呀!下面我们还结合图形还分析,从图中我们可以看出,在△HGF中,PG+HG=HG+GF>HF=PM+MH。而由于点I的位置关系,GI>HG。同理在△EIM中,PI+IM=EI+IM>EM=EH+HM。而由于点I的位置关系,GI>IM。
根据图形可见,走△PMH距离最短。
同学们,是不是通过作图分析这样的题型,更有利于我们轻松找到解题思路和解题办法,更便于记忆,更有利于我们找到快速有效的学习方法。
总之,在教学过程中,促进学生对知识充满好奇心,对新旧知识能更好地融会贯通,对新知识能更快地消化吸收,让学生学起来不感觉吃力,使课堂上有其乐融融的学习情境,使学生能形成良好的思维习惯、应用意识和探索数学的能力与精神,让他们的数学素质不断提升。
编辑 韩 晓