开发数学课题学习素材的实践与思考

杨一丽

现阶段我国中学数学教材虽然逐步成熟，但针对学生个性发展和可持续发展的元素成分还有待于改进和提高.从国际形势来看，世界上最有影响力的国际学生评价项目——PISA评估的重点不是传统数学课程中的数学知识和技能，而是更多地关注学生的思维能力和创新精神、洞察力等.现阶段承载如此重要任务的课程内容是“综合与实践”，“课题学习”是“综合与实践”的主要呈现形式.而目前课题学习资源却很匮乏，所以如何有效开发并利用好此类资源成为我们必然要解决的一个问题.笔者将结合开发课题学习素材的实践与思考谈谈自己的想法.

一、开发课题学习素材的原则

（一）专业性与综合性相结合

数学知识是一个有机的整体，课题学习的内容应与初中数学的核心内容和思想方法紧密关联，一定程度上可将原有的专业知识体系掘深拓宽.《课程标准》指出：学生能够体会数学知识之间、数学与其他学科之间、数学与生活之间的联系，运用数学的思维方式进行思考，增强发现和提出问题的能力、分析和解决问题的能力.因此课题学习的素材除其独特的专业性外，还要有一定的综合性.它可以是各学科之间的综合，如浙教版教材中“怎样选择较优方案”、“会徽中的数学”等.

（二）适切性与探究性相结合

在课题学习设计过程中，必须充分考虑学生的年龄特征，相关的知识、能力及活动经验的状况，同时内容应具有进行深入学习、探究的可能性.题目中问题的设计应能够激发学生深层次的思考，使学生能够通过科学的自主探究过程逐步解决问题.既要使学生获得问题解决后的、积极的情感体验，同时又要注意避免背离数学的本源而追求形式上的“无谓探索”.

（三）现实性与应用性相结合

《课程标准》指出，综合与实践内容设置的目的之一在于培养学生综合运用有关知识分析问题、解决问题的能力，培养学生的应用意识和创新意识.让学生体会数学与现实世界的联系，树立正确的数学观是课题学习的另一个重要目标.因此，课题学习类素材应该是现实的、富有挑战性的，同时还应该具有良好的生活内涵.这有利于学生体会数学来源于生活又服务于生活，体现课程的人文精神与德育价值，同时拓宽了学生的学习领域，激发学生学习数学的兴趣.

（四）开放性与发散性相结合

好的课题学习素材应具有问题解决方式的多样化和问题结论的开放性的特点.多种问题解决的方法有利于培养学生思维的发散性，而开放性的问题，更利于不同学生从中获得成就感和自信心，这也是深入开展课题学习的重要保证.

二、开发课题学习素材的方法

（一）从课本内容入手拓展

在教材中编录或涉及了许多适合课题学习的经典材料，但由于篇幅和课时等限制，教科书中通常是以定理、阅读材料等形式简单包装.如勾股定理、费马点、杨辉三角等，只要教师多留心，许多内容俯拾皆是.当然最关键的还是后续设计的问题富有思考性，能引发学生进行有价值的思考，发展问题意识，培养创新精神.如“探索勾股定理”，我们可以编拟如下的系列问题进行课题学习.

案例1   勾股定理与拼图

问题1：如图1是在北京召开的第24届国际数学家大会（ICM-2002）的会标，其主体图案的设计思路可追溯到3世纪中国数学家赵爽所使用的弦图，你能借助这个图形证明勾股定理吗？

问题2：利用四个全等的直角三角形，还可以拼出哪些正方形？你能利用它们证明勾股定理吗（图2）？

问题3：如图3是美国总统1876年给出的一种验证勾股定理的方法，你能利用它验证勾股定理吗？这种方法与拼正方形的方法证明定理有什么联系呢？

问题4：如图4是我国古代的“青朱出入图”，你能理解其中的奥妙吗？

（二）从历史经典问题入手拓展

数学是一门历史性和累积性很强的学科.追溯古今，每一个数学经典问题都闪耀着人类思想的光辉，许多数学经典问题都从绝境中突破，折射出不屈不挠的精神和人类的睿智，如七巧板、无理数的发现、微积分和非欧几何的创立等.正如英国科学史家丹皮尔（W.C.Dampier）所说的：“再没有什么故事能比科学思想发展的故事更有魅力了.”所以加强对这些知识产生、发展过程的了解并能创设符合学生实际的深度拓展，达到借鉴经典、增强信心、培养能力的学习效果.

案例2  七巧板

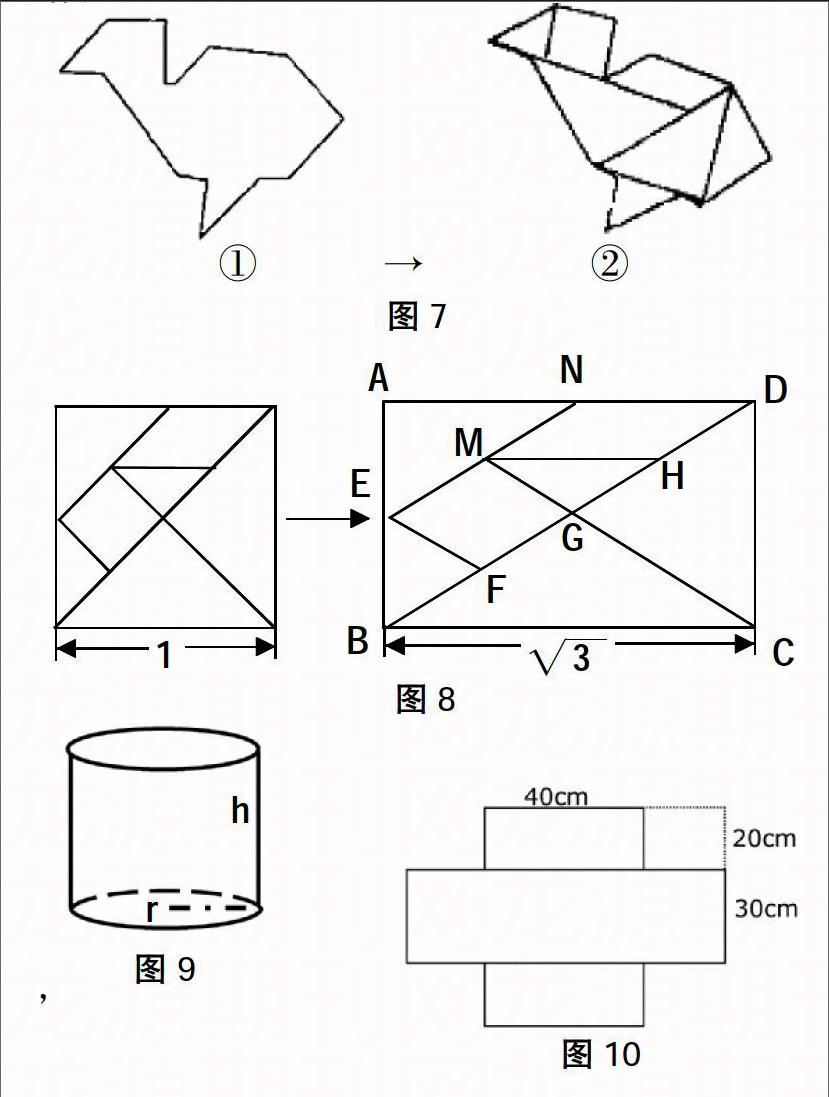
七巧板起源于我国唐宋时代，古代称作“燕几图”.如图5，它由五个等腰直角三角形、一个正方形和一个平行四边形共七部分组成.19世纪初，七巧板流传到西方，被称为“东方魔板”，成为中华民族智慧的一个代表.

问题1：如图5，用边长为 1的正方形纸板制成一副七巧板，将它拼成小天鹅图案，其中阴影部分的面积为多少？

问题2：如图6是一副七巧板，若△BIF的面积为1.

（1） 一只蚂蚁从点A沿A-B-F-H-E路线爬行，求蚂蚁所走过的总路程;

（2） 两只蚂蚁分别从G，E两地出发爬行，若它们在AC上相遇，则如何行走，使得它们走过的总路程最短？

问题3： 如图7①是由七巧板拼成的鸡形图.

（1） 在图7①中将七巧板的七块部件分割出来.

（2） 已知小鸡鸡尾三角部分面积为2a2（a为有理数），求整个小鸡的面积.并求出七块部件各边长中最小的无理边长及最大的内角.

（3） 请用这副七巧板，既不留一丝空白又不互相重叠，拼出至少2种边数不同的凸多边形.

（4） 有人在玩七巧板时发现：“七巧板拼成的多边形，其边数不能超过8.”你认为这个结论正确吗？请说明理由.

借助以上探究，进一步可得有关七巧板的四个结论.

结论1：若16个基本三角形组合成一个凸多边形，则任一三角形的有理边会和另一三角形的无理边重合.endprint

结论2：由16个基本三角形组成的凸多边形，其每条边要么全是由基本三角形的有理边组成，要么全是由基本三角形的无理边组成.

结论3：由16个基本三角形组成的凸多边形，其边数不超过8.

结论4：如果16个基本三角形组成一凸多边形，则该多边形可内接于一个矩形，该多边形的所有有理边或者无理边就是该矩形的4条边.

问题4：1999年，数学家伯纳德·魏祖克对七巧板图形进行了变换，把边长为1的七巧板在一个方向上放大为倍，另一方向不变，如图8，将变换后得到的七巧板称为三角七巧板.

（1）求出三角七巧板七块部件中最小的内角度数;

（2）找出图中所有的相似图形;

（3）求△MHG的面积;

（4）若用这副七巧板，既不留一丝空白又不互相重叠地拼多边形，边数最多为几条？

（三）从实际生活问题入手拓展

数学的不断发展，主要通过两种方式：一是数学形式的演变，二是现实中的问题.有时形式先于问题，有时问题又先于形式.既然数学是这样发展的，那么我们很自然地应该顺着它的发展轨迹去认识数学、学习数学、研究数学.现实问题需要人们掌握更多的数学知识，成本、利润、投入、产出、贷款、效益、股份、市场预测、风险评估等一系列经济词汇被频繁使用，且各类统计图表正在生活中传递着重要信息，数学已经进入人们生活的方方面面.这就需要我们用敏锐的眼光去观察世界，用数学语言去表达实际问题中的数学关系，建立数学模型.

案例3  商品包装

生活中我们经常能够见到近似圆柱体、长方体、正方体的包装容器，如易拉罐、水杯、各种包装盒等. 在设计这些容器时，除了考虑到美观、实用外，还有一个很重要的问题：如何设计能够使这些容器在体积不变时，表面积最小;或表面积不变时，体积最大，以节省材料.积少成多，这将会对能源、环保做出巨大贡献.

问题1：如图9，假设容器是标准的圆柱，忽略包装材料的接缝，容积就等于体积，这样就把问题简化成一个数学问题：“体积一定的圆柱，底面半径与高的比为多少时表面积最小？”

问题2：将圆柱形的容器改为没有上盖，问题1就变为 “体积一定的圆柱，底面半径与高的比为多少时一个底面与侧面积和最小？”

问题3：经过市场调查，常见的饮料容器底面比侧面厚一些，有的饮料容器底面比侧面的材料硬一些，所以底面的单位造价会比侧面贵，为了方便研究，可以将以上的几种情况都转化为：“体积（容积）一定的圆柱形容器，底面的单位造价是侧面单位造价的k倍，半径与高的比为多少时表面总造价最小？”

问题4：用一张长80cm，宽50cm的长方形铁皮做一只无盖长方体铁盒（焊接处的厚度和损耗不计），问这只铁皮盒尽可能大的体积是多大？

（1）学生们提出了如下方案.

①为了不浪费铁皮，将在长方形铁皮四周剪下的四个全等的小正方形剪成小长条，焊接到长方体的上口，增加了长方体的高度，经计算可以增加体积4000cm3，这时体积可达22000cm3.

②如图10，将4个小正方形，两两分别焊接到上、下面中间，这时V=30×40×20=24000（cm3）.

③可以设要做的长方体的长、宽、高分别为a，b，c，则ab+2bc+2ac=4000.

∵4000=ab+2bc+2ab≥3，

∴V=abc≤=24343.2（cm3）.

此时ab=2ac=2bc，即a=b=2c.代入ab+2ac+2bc=4000，得a=b=，c=.

这是一种理想化的模型，它是以上几种情形中最大的，此时长方体的底面是正方形.

（2）反思提炼.

请你分析上述出现的结果的合理性.

① 第3种情况虽然体积最大，但焊接环节太多，质量无法得到保证.

② 第2个方法更适合，既节约了成本，又使体积尽可能大.

这是一个开放性的问题，我们可以渗透实际元素，从不同角度来理解与分析，从而对问题有了更高的认识.

总之，选定的课题学习素材应该在学生认知领域内，适合学生进行数学化的活动，使得活动真正地体现数学思想和方法，从而真正地成为研究问题的载体. 在确定素材后，科学地设计问题，激活学生的思维，及时引导学生在探究过程中学会发现问题、提出问题、分析问题、解决问题，以提高其思维的发散性和创造性.除此以外，在评价方面应多采用赏识性语言，以发挥评价的激励性作用，促进学生的健康成长.endprint