基于初中数学概念教学关键点杂谈
2015-06-16胡淑芳
胡淑芳

[摘 要] 如何实施数学概念教学?本文从合理设置概念教学方向性出发,从让学生认识概念逻辑性、区分概念层次性、理解概念抽象性、领悟概念扩展性等方面进行深度概念教学,深化概念教学,进而认识数学概念的本质和内涵.
[关键词] 数学;概念;新课程;抽象性;逻辑性;层次性;扩展性
新课程对于数学概念教学的理念是:积极探索、主动建构. 这一理念在新课程积极推广之初获得了教师的普遍支持和实施,随着教学改革热情的渐渐趋于平淡,以及应试的依旧存在,笔者发现不少教师渐渐对数学概念教学的探索式实施越来越不关注,或仅仅只在公开课进行课程理念教学示范,而在常态课阶段,教师以传统的概念讲解—典例分析—大量训练—变式巩固来进行数学概念教学. 这种方式短期内获得了一定的效果,因此依旧备受教师的青睐. 江苏省数学特级教师李庾南在谈及新课程数学概念教学时说:很多教师不是在教数学概念,而是在教如何模仿做题. 概念没教懂,只似懂非懂地教学生解题,这样的概念教学方式是误人子弟. 教概念,要教会学生理解数学概念为什么这么定义,教会学生这些概念如何从实际情境中抽象而来,教会学生自我发现、认知的过程等. 笔者认为,李老师的一席话极大地指明了我们现阶段数学概念教学的短板和不足,并没有给学生指明概念学习的道路,而是用不断重复训练的手段在磨灭概念学习过程中的创造力,因此,本文将结合案例和笔者自身的一些实践,系统而严密地谈谈概念教学中必须倚仗、改变的一些关键要素,让学生在清晰获得概念的过程中,增强数学学习的学习力.
概念逻辑性的认识
教数学概念一般都会教两个方面,即概念的内涵与外延. 众所周知,内涵指的是数学概念的本质属性,它着重强调学生对于数学概念抽象的理解;外延指的是数学概念所包括的所有对象,指出了我们所要研究的对象的总和. 笔者在教学中发现,有些学生无法清晰地将概念的内涵和外延弄清楚,例如,一次公开课上,笔者听到某老师在谈到有理数和实数这两个数学概念教学时,教师问■,■,-2是否是有理数?是实数吗?学生甲无法正确区分有理数和实数,教师则大声呵斥学生:怎么连这两者都无法区分?然后又面对其他学生问同样的问题,结果依旧出现不少学生无法正确区分. 此时,该教师匆匆忙忙将上述三个数字分类后直接结束了相关课程. 笔者惊讶的是:若少数学生没有区分清楚,那是正常的教学现象,教师可以通过回顾、复习帮助学生回忆,但假如不少学生都无法正确区分有理数和实数这两个数学概念,笔者认为该教师在概念教学的逻辑性上存在着较大的问题,仅靠一味地做相关数学题目无法解决这种教学现象. 而且,会在后期类似的教学过程中出现类似错误. 因此,笔者认为,要讲清概念的逻辑性,应该尊崇从大到小的原则(即从大概念到小概念,一般称之为种概念到属概念),将后续附加条件、特征(称之为属差)进行渗透,这样,在概念逻辑性上的认识才是比较完整和有框架的. 如讲解四边形概念时,先介绍种概念平行四边形,给出属差①:若邻边相等是什么?得到属概念①菱形;给出属差②:若有一个内角是直角?得到属概念②矩形;给出属差③:邻边相等且有一个角是直角是什么图形?得到属概念③正方形.
概念教学只有抓住属差和种概念,才能将逻辑性的渗透做到清晰、有条不紊,这样存储于学生脑海中的知识才不会是凌乱、无框架的,可以使相关概念的储藏条理化、系统化、网格化,也不会出现类似上述教师关于数学概念有理数和实数教授不清的状况.
理解概念抽象性
我们知道,数学概念之所以简捷,是缘自其强烈的抽象性,它把生活中各种具备具体形态的物体、性质经过提炼、抽象,用形式化的语言表述,从而形成了具备共性、本质的数学概念. 比如,从圆的面积公式找到了其与半径之间的关系式、正方形面积与其边长之间的关系式等,这些抽象出来的关系式所阐述的就是学生后来了解的函数关系式,其本质就是研究一个变量经过不同的对应关系得到另一个变量的过程. 笔者认为,函数概念正是中学数学中理解概念抽象性最重要、最核心的一个数学概念,数学家莱布尼兹用了多年,在此之前很多数学家都没有能够清晰地弄清楚函数概念,因此,要学生在短时间内掌握函数概念的抽象本质有一定的困难. 依据学生特有的心理特征,为了扎实地理解函数概念的抽象性,可以借助一些感性的实物模型、教具等,将抽象性的特点以具体形态展示出来. 笔者认为,函数概念的变化其实可以看成一种原材料的加工机,比如将自变量x寓意成石块原料,经过加工机得到不同的函数值(可以看成石板、粉尘、石头雕像等),这些不同的加工孕育出了不同的函数,这样的形象解释有助于心理结构比较感性的中学生进行理解,也有助于他们进一步学习函数知识.
领悟概念扩展性
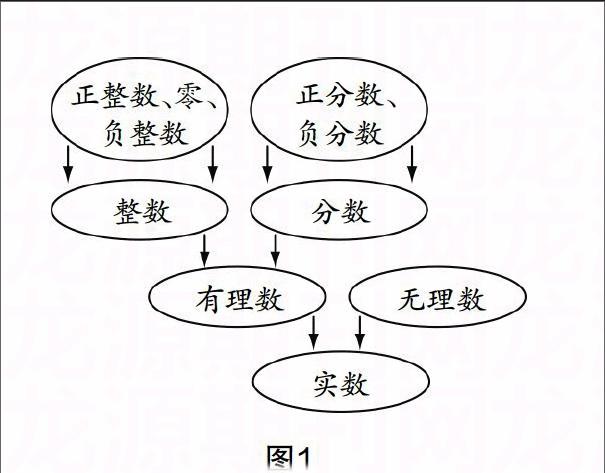
数学概念的内涵与外延是相辅相成的,而且存在着相互压缩的依赖关系,即概念的外延多则内涵相对少,概念的外延少则内涵相对多. 比如,三角形是一个大概念(种概念),其属性相对较少;等腰三角形是个较小的属概念,其属性相对而言就多了;正三角形是再小的属概念,其要求三条边相等、三个角相等,这些共同属性就更多了. 从这一概念的扩展我们知道,概念教学需要抓住其扩展性来研究. 例如,我们在研究数出现的过程时,利用概念外延不断扩大的过程进行概念的逐一呈现(见图1).
再比如,对于图形认识中出现的四边形概念,这是一个概念外延收缩的过程(如图2). 上述两个案例向教师指出了在教学中某些概念的教学必须尊崇一定的概念收缩或扩散原则,利用图形化的结构图梳理知识的系统化、严密化,能让概念之间的种、属位置关系利用内涵特征进行合理地区分与辨别,这种合理的扩展性领悟大大加深了学生对于某一知识体系概念的理解、加深和记忆. 笔者认为,教师将此类种属概念明确的知识体系放在一种典型的树状图教学,对于学生真正理解这些概念、牢记这些概念,进而将这些概念内化在自身知识体系中,对于概念的合理扩展等大有帮助.
总之,新课程尽管从理论上加深了数学概念要提高效率的指导性方向,但在具体教学中或多或少被应试所影响,笔者认为,解题很重要,但不能替代概念教学的合理性,因此以本文所阐述的三方面拙见,让教师在概念教学关键之处进行一些细致地实施,让学生在茫茫题海中适当解脱出来,真正领会形式化概念的本质.endprint
