EMD在叶绿素光谱信号去噪中的应用

翟哲 李伟凯 李长凯 裴玉

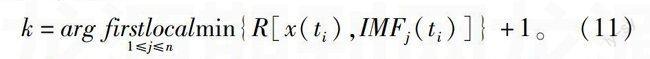
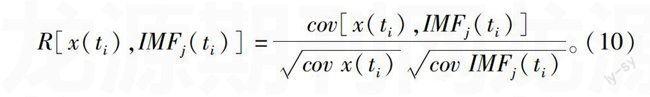
摘要：基于每个IMF自关联函数的特征，提出了一种新的EMD去噪方法。以检测苗期玉米叶片叶绿素含量为例，首先对原光谱信号采用SNV+Detrending方法进行预处理，然后利用该方法对预处理后的信号进行去噪，并与小波去噪方法和EMD融合小波去噪方法进行对比，最后应用偏最小二乘回归方法进行校正模型的建立。结果表明：将该方法应用到实际近红外光谱信号去噪中，其预测集决定系数（r2）达到0.984，残差均方根RMSE为0.075，证明该方法在近红外光谱处理过程中具有很好的去噪效果，建立的校正模型具有较高的鲁棒性和推广性。

关键词：经验模态分解;自适应;近红外光谱;叶绿素

中图分类号： S126 文献标志码： A

文章编号：1002-1302（2015）04-0392-05

收稿日期：2014-05-25

基金项目：黑龙江八一农垦大学研究生创新科研项目（编号：YJSCX2013-16BYND）。

作者简介：翟 哲（1988—），男，黑龙江庆安人，硕士研究生，主要从事数据处理研究。E-mail：zhai_zhe@163.com。

通信作者：李伟凯，博士，教授，博士生导师，主要从事光电检测研究。Tel：（0459）6819009;E-mail：bynd@263.net.cn。

随着计算机科学技术的飞速发展，近红外光谱技术在仪器分析领域受到了有关专家的高度重视[1]。近红外光谱技术之所以能迅速发展并在各个行业都有广泛的应用，是因为它有很多的优越性[2]。但是由于外界环境的影响，近红外光谱仪所采集到的光谱信号，除了包含自身信息外，在测量中还不可避免地得到许多无关的噪声信号[3]。因此在使用化学计量方法建立校正模型时，消除光谱数据无关噪声在光谱数据分析中变得十分关键和必要。本研究将改进经验模态分解（empirical mode decomposition，EMD）方法引入到近红外光谱信号去噪中，旨在探索近红外光谱信号去噪的新方法。

1 基本思想

EMD方法就是把1个非线性非平稳的信号分解为有限个本征模函数（intrinsic mode function，IMF）分量和1个趋势项[4]，原始信号x（t）可表示为：

x（t）=∑ni=1ci（t）+rn（t）。

（1）

式中：ci（t）為第i个IMF分量;rn（t）为筛选到最后剩下的趋势信息;t为时间;n为分解的IMF个数。各个IMF分量都代表信号从高频到低频的分量，通常情况下阶数较小的IMF代表高频分量和噪声信号，阶数较大的IMF代表低频分量，受噪声影响较小。

EMD其实就是把信号的极值特征尺度作为度量而进行筛选的过程，信号从最小特征尺度实行筛选，因此得到周期最短的IMF[5-6]。之后再进行逐层筛选，最终获得周期尺度渐次增大的多个IMF，此过程亦显示出了多分辨辨识的滤波全程。这个途径是依据信号分解的IMF分量建构滤波函数，所以能极大保持信号固有的非线性、非平稳特征。

假设x（t）为含噪信号，则经过EMD算法的分解后其高通滤波表达如下：

xhp（t）=∑ki=1ci（t），（1

（2）

带通滤波表达如下：

xdp（t）=∑ki=hci（t），（1

（3）

低通滤波表达如下：

xlp（t）=∑ni=kci（t）+rn（t），（1

（4）

但是，噪声同信号在IMF分量内叠混，可以用EMD阈值去噪的方法[7]。其中在阈值选择方面，根据Donoho等给出的小波去噪中的阈值[8]，其中小波去噪软阈值为：

ysoft（t）=sng[x（t）]·[|x（t）|-δ]，|x（t）|>δ

0，|x（t）|≤δ。

（5）

式中：δ为通用阈值。

在第j层选取δ=σj2lnN。

式中：N为信号的长度;σj为噪声在第j层的标准差，可利用σj=media/0.674 5进行估计，media为第j层上小波系数的绝对中值。

因此，将这个等式略加改变后运用至IMF去噪上，即获公式：

imf ′j=sng[imfj（i）]·[|imfj（i）|-δ]，|imfj（i）|>δj

0，|imfj（i）|≤δj。

（6）

式中：δj为第j个分量imfj的阈值，由下式可以计算：

δj=σj2lnN=media[abs（imfj）]0.674 5×2lnN。

（7）

式中：media为第j个imfj分量上的绝对中值。

2 基于能量最小原则的EMD自适应去噪方法

信号经由EMD算法进行分解后，可获得可数的频率由高至低的IMF，它们中阶数较低的IMF与信号的高频成分相对应，普遍涵盖了信号尖锐部分或噪声;阶数较高的IMF与信号的低频成分相对应，低频成分中噪声能量较弱。EMD去噪的首要内容即为针对大部分含噪信号，它的主要能量累积在低频段范围内，越往高频范围，它所蕴含的能量便越小。假设信号区和噪声区的分界点为k，因此肯定有1个IMFk分量，让这个分量之后的IMF里的信号成为主导模态，而在这之前，IMF里的噪声则是主要模态，因此原始的基于EMD进行去噪的目的即为发现IMFk。

Boudraa等首先提出连续均方误差（consecutive mean square error，CMSE）准则的EMD去噪法，这种方法利用了IMF能量的全局极小值位置作为噪声起主导作用与信号起主导作用的分界点[9]。文献[9]和文献[10]都采用了连续均方误差准则这种方法，对信号成分发挥主导功能模态和噪声成分发挥主导功能模态进行了区分，利用反映信号主要结构的模态对信号进行部分重构以实现去噪。文献[9]将全部IMF能量的最小值点对应的模态当作信号成分与噪声成分的分界点，但是判断准则可能存在偏差，主要体现在2个方面：首先，若CMSE在全局极小值前面有局部极小值，则局部极小值对应的位置应加1;其次，如果不存在局部极小值，则全局极小值对应的位置应加1。因此文献[10]在文献[9]的基础上做了一些改进，采用首个局部极小值点对应的模态作为分界点，若在全部极小值前存在着局部极小值时，则有：

k=argfirstlocal1≤j≤n-1min[CMSE（xj，xj+1）]+1;

（8）

否則：

k=argmin[CASE（xj，xj+1）]+11≤j≤n-1。

（9）

式中：firstlocal表示首个局部极小值。

但是在试验中不难发现，文献[10]中提出的改进方法与其采用的连续均方误差有关，信号模态和噪声模态分选准则仍然存在一定的偏差。对此文献[11]对基于各IMF与所给信号相关系数的大小进行了修正：它考虑到文献[10]的分选准测，信号在低信噪比情况下存在的问题，因此选择各阶模态与原始信号之间的相关系数作为噪声模态与信号模态的分选准则来代替能量法的连续均方误差准则，从而减轻因信号模态能量较小而被舍弃的概率。各阶模态函数与原始信号的相关系数定义如下：

R[x（ti），IMFj（ti）]=cov[x（ti），IMFj（ti）]cov x（ti）cov IMFj（ti）。

（10）

式中：cov（·）代表协方差，噪声模态与信号模态的分界点k由公式（11）确定：

k=arg firstlocal1≤j≤nmin{R[x（ti），IMFj（ti）]}+1。

（11）

主要步骤：首先，对原信号进行经验模态分解;其次，以各阶IMF与原信号的相关系数曲线中第1个极小值点的位置作为标准，找到噪声主导模态和信号主导模态的分界点;最后，将IMF中信号起主导作用的模态成分进行重构来实现去噪。

这些方法在相当程度上都解决了基于EMD算法进行滤波去噪的自适应滤波器终结阶数k不好界定的问题。如果信噪比较高，此判别法较为有效，但是在噪声污染太重的低信噪比前提下，这个办法的功能并不是很稳固。这是由于低信噪比时，可用信号能量极少，由EMD算法分解而来的IMF模态中，有的IMF能量差别较小，即便是某个IMF的能量达到局部最小值，却也并不一定对噪声起主要作用。因此，选取此IMF后面的IMF来实现重构时，将可能导致有用信息遗失。更重要的是，在某些特殊条件下，难以发现IMF能量全部极小值，此时这种方法完全行不通。同时，噪声和有用信号在IMF分量里有时有混叠行为，而如果依然用原方法除去一些IMF，就会误删某些有用信号的高频成分，破坏信号的完整性，从而达不到良好的去噪效果。

基于EMD去噪的主要目的就是寻找信号主导模态与噪声主导模态的分界点k，但是鉴于含有高斯白噪声的信号应用EMD算法进行分解时，由于EMD算法的自适应性和强制信号的上下对称性，使分解而来序数小的蕴含噪声的IMF里，高斯白噪声特征被毁坏，获得非真正意义上的白噪声分量。只是白噪声统计特征仍近似留存，也就是其在零点处自关联函数为最大，别处虽然不为0，但是相对零点处的自关联函数值的关联性已很小，极速衰减。对于普通信号，它们的自关联函数在零点处获得最大值而在其他地方则并不一定为0，它会随时间差的变化而改变。鉴于这些特征，本研究依据每个IMF自关联函数特征，提出基于能量最小原则的EMD自适应去噪方法，我们在断定噪声发挥主要功能的IMF模态中，它的构成成分除噪声外，还包含少数有用信号的高频部分。至此，对于噪声模态分量筛选的所有阈值，运用去噪法把想除去的IMF分量实行滤波，再将全部经过处置和未处置的IMF分量实行重构，从而获得去噪的信号。其算法步骤为：（1）对含噪信号应用EMD算法进行分解，得到n个IMF分量;（2）按照公式10所示，分别计算各阶IMF自相关系数;（3）依照能量的积累高低，由公式11断定信号主导模态和噪声主导模态分界点k;（4）把噪声主导模态的IMF对细节系数取1/3进行抑制，获取去噪后的IMF分量;（5）信号主导模态IMF分量与去噪后的IMF分量相加，重构原信号。

3 结果与分析

3.1 光谱采集与预处理

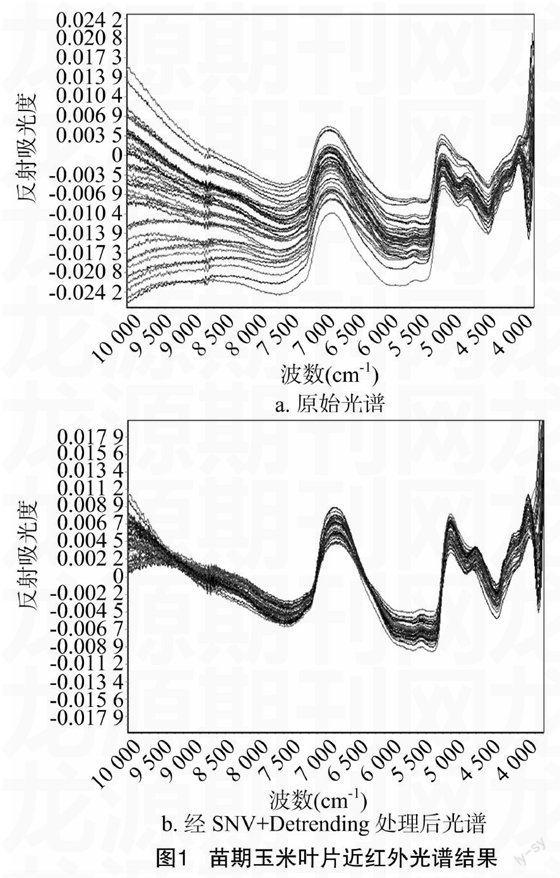
使用北京瑞利分析仪器公司生产的WQF-600N傅立叶变换近红外光谱仪（波数范围3 300～10 000 cm-1，分辨率优于4 cm-1）来进行近红外光谱数据的采集，仪器自带MainFOTS软件，可将采集到的光谱数据保存到计算机中。试验选取样品为同一生长期各种不同外观、形状的苗期玉米叶片，共计42张，42张苗期玉米叶片的原始光谱结果见图1-a。

从图1-a可以看出，所采集的原始近红外光谱信号中包含了样品组成的特征信息，但是基线漂移严重，并且还包含由温度、湿度、时间、样品背景等影响而造成的许多与信号无关的噪声，因此分析偏差较大。所以本研究先对原始光谱数据实行预处理的规范化工作，然后对规范化后的光谱数据进行去噪处理。

比较常用的数据规范化方法有变量标准化（SNV）、趋势变换法（Detrending）、SNV+Detrending、中心化（MC）、归一化等方法，通过对比验证、比较效果，试验已经证明SNV+Detrending 预处理方法优于其他预处理方法。因此本研究先对原始光谱先进行数据规范化，这样就可以消除变异程度从而实现数据规范。图1-b为采用SNV+Detrending方法预处理后的光谱结果。

从图1-b可以看出：实行规范化后的光谱基本除去了部分线性或接近线性的背景噪声对目标光谱的影响;但是经过处理后光谱的噪声并没有消除，因此还要对预处理后的光谱进行消噪处理。

3.2 光谱信号去噪

为了对基于能量最小原则的EMD自适应去噪效果进行比较，本研究对全部光谱进行去噪。下面采用此方法对10号苗期玉米叶片样品进行EMD自适应去噪处理，10号苗期玉米叶片样品预处理后的光谱经过EMD算法分解后，得到6阶imf（imf1～imf6）分量和1个残余项（imf7），每个IMF都有不同的振幅和频率，分解按照频率从高到低自适应地进行，然后自适应地选出分界点，进行抑制和重构。从去噪后的光谱图（图2-c）可以看出，光谱非常光滑，噪声基本上得到了消除。其中10号样品预处理后的光谱图、6阶模态函数、去噪后的光谱结果分别如图2-a、图2-b、图2-c所示。

采用同样的方法对其他41组样品预处理后的光谱图做了去噪处理，为了作对比，给出了10號样品预处理后光谱的小波去噪、EMD融合小波去噪、基于能量最小原则的EMD自适应去噪方法的去噪效果图。从图3可以看出，基于能量最小原则的EMD自适应去噪方法去噪效果最好，几乎完全消除了噪声的干扰，在去除大部分噪声的同时对光谱的峰形没有太大影响，而且反映原始信号的特征尖峰点得到很好的保留。小波去噪、EMD融合小波去噪的去噪效果也较好，对峰形也没有太大影响，但母小波的选择对去噪效果影响很大。相比之下，基于能量最小原则的EMD自适应去噪方法是最有效的，光谱平滑性增强，且对光谱的峰形没有太大影响。与其他2种方法相比，基于能量最小原则的EMD自适应去噪方法具

有完全自适应性，这就避免了选择母小波的麻烦，增加了分析结果的可靠性。

通过对规范化后的光谱信号进行去噪处理，可以滤除其含有的无关噪声信号，从而降低噪声对光谱分析的干扰，充分提取有效信息，有利于建立最佳数学模型，提高分析的准确度。

3.3 玉米叶片叶绿素含量检测

从编号的42个苗期玉米叶片样品中随机抽取6号、9号、10号、17号、26号、32号、35号、37号、39号、40号这10个样品作为预测集，用于检验方程的可靠程度，其余32个样品作为校正集，用来进行校正模型的建立，下一步建立校正模型的校正样本和预测样本散点图。

采用OPUS软件建立叶绿素偏最小二乘回归模型，图4、图5、图6为用偏最小二乘回归法[12]所得到的苗期玉米叶片叶绿素含量校正样本和预测样本的散点图，其中图4、图5、图6分别是使用小波去噪、EMD融合小波去噪、基于能量最小原则的EMD自适应去噪的散点图，可以看出苗期玉米叶片预测集和实测集的相关性。表1列出了3种预处理方法苗期玉米叶片叶绿素含量预测值和实测值的比较结果，可以看出，经过基于能量最小原则的EMD自适应去噪后，光谱分析的准确性明显提高。结果表明，采用基于能量最小原则的EMD自适

应去噪方法建立模型对预测样品进行预测的准确性明显得到了改善。

应用决定系数r2和残差均方根RMSE作为评价偏最小二乘回归模型优劣的标准。经基于能量最小原则的EMD自适应去噪后，预测值与实测值之间的决定系数r2为0.984，残差均方根RMSE为0.075。试验数据说明，该模型对苗期玉

米叶片叶绿素含量有较好的预测效果，提高了叶绿素近红外检测的鲁棒性。

4 结论

本研究以苗期玉米叶片近红外光谱为研究对象，将EMD去噪新方法应用到叶绿素近红外光谱分析中。首先对原始光谱图用SNV+Detrending方法进行规范化预处理，实现数据规范;其次将新方法应用到规范化后的光谱去噪中，并与小波去噪方法和EMD融合小波去噪方法进行比较;最后采用偏最小二乘回归方法进行了校正模型的建立，测量叶绿素含量。结果表明，采用基于能量最小原则的EMD自适应去噪方法进行近红外光谱数据去噪是可行的，此方法比采用传统的去噪方法有更高的预测精度。EMD方法在红外光谱处理中可以有效地消除噪声的影响，提取光谱中的有效信息，在光谱数据处理中将会有更广阔的应用前景，从而为下一步研究打下良好的基础。

参考文献：

[1]高荣强，范世福. 现代近红外光谱分析技术的原理及应用[J]. 分析仪器，2002（3）：9-12.

[2]张小超，吴静珠，徐 云. 近红外光谱分析技术及其在现代农业中的应用[M]. 北京：电子工业出版社，2012.

表1 预测集样品的预测结果

样品序号 实测值

（mg/g）

小波 EMD融合小波 EMD自适应

预测值

（mg/g） 绝对误差

（mg/g） 预测值

（mg/g） 绝对误差

（mg/g） 预测值

（mg/g） 绝对误差

（mg/g）

6 2.174 1 2.383 4 0.209 3 2.285 4 0.111 3 2.083 7 -0.090 4

9 2.184 1 2.3729 0.188 8 2.280 4 0.096 3 2.252 8 0.068 7

10 1.706 1 1.562 8 -0.143 3 1.796 7 0.090 6 1.754 4 0.048 3

17 3.298 5 3.176 2 -0.122 3 3.217 3 -0.081 2 3.241 2 -0.057 3

26 3.253 6 3.132 8 -0.120 8 3.331 4 0.077 8 3.326 1 0.072 5

32 2.276 9 2.172 7 -0.104 2 2.417 4 0.140 5 2.159 5 -0.117 4

35 2.607 3 2.726 7 0.119 4 2.691 2 0.083 9 2.696 8 0.089 5

37 2.401 7 2.265 5 2.119 7 -0.145 8 2.146 7 -0.118 8 2.208 2

39 2.265 5 1.449 5 1.339 8 -0.109 7 1.380 7 -0.068 8 1.395 5

40 1.449 5 2.972 9 2.874 9 -0.09 8 2.872 6 -0.100 3 3.035 6

r2 0.942 0.971 0.984

RMSE 0.141 0.099 0.075

[3]李 勇，魏益民，王 锋. 影响近红外光谱分析结果准确性的因素[J]. 核农学报，2005，19（3）：236-240.

[4]Huang N E，Shen Z，Long S R，et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Soeiety of London，Series A，1998，454：903-995.

[5]高忠剑波，蔡宗平. 运用Hilbert-Huang变换的振动测试分析系统[J]. 工业仪表与自动化装置，2009（3）：88-90.

[6]杨志华，齐东旭，杨力华. 一种基于Hilbert-Huang变换的基音周期检测新方法[J]. 计算机学报，2006，29（1）：106-115.

[7]邵忍平，曹精明，李永龙. 基于EMD小波阈值去噪和时频分析的齿轮故障模式识别与诊断[J]. 振动与冲击，2012，31（8）：96-101，106.

[8] Donoho D L，Johnstone L M，Kerkyacharian G，et al. Wavelet shrinkage：asymptopia？[J]. IEEE Transaction on Information，1995，41（3）：613-627.

[9]Boudraa A O，Cexus J C. EMD-based signal filtering[J]. IEEE Transactions on Instrumentation and Measurement，2007，56（6）：2196-2202.

[10]孙伟峰，彭玉华，许建华. 基于EMD的激光超声信号去噪方法[J]. 山东大学学报：工学版，2008，38（5）：121-126.

[11]陈凤林. 一种新的基于EMD模态相关的信号去噪方法[J]. 西华大学学报：自然科学版，2009，28（6）：20-24.

[12]张 银，周孟然. 近红外光谱分析技术的数据处理方法[J]. 红外技术，2007，29（6）：345-348.