基于距离判别的煤层压裂选井选层新方法

2015-06-15李吉雄李铁军谢寿昌杨武剑施生伟

断块油气田 2015年5期

李吉雄，李铁军，谢寿昌，杨武剑，施生伟

（1.西南石油大学理学院，四川成都610500；2.中国石油新疆油田分公司开发公司，新疆克拉玛依834000）

为了有效开发煤层气资源，需要对煤层进行增产改造，水力压裂是首选方法和主要措施［1-5］，所以，对煤层压裂选井选层方法的研究意义重大［6-7］。对于常规油气层，前人建立了一些压裂选井选层模型，如经验法、模糊识别法和人工神经网络法等［8-10］。而对于煤层气井，压裂选井选层则主要依靠以往经验或生产需求，具有一定的主观性、盲目性和风险性［11-14］。在对影响煤层气井产气量的参数进行综合分析的基础上，本文结合距离判别分析理论，建立了判别高、中、低产井层的准则，为煤层压裂选井选层提供有效指导。

1 距离判别分析理论原理

距离判别分析方法属于判别个体所属群体的一种多元数据分析方法，能从各训练样本中提取各总体信息，科学地判断所得样品的所属类型，近年来在自然科学、社会学及经济管理学科中都有广泛应用［15-17］。

1.1 多总体的距离判别分析理论

设有g 个p 维总体G1，G2，…，Gg，均值向量分别为μ1，μ2，…，μg，协方差矩阵分别为Σ1，Σ2，…，Σg。设x 为一个待判样本，计算x 待判样本到各总体的距离，比较g 个距离，判定x 属于与其距离最短的总体（若最短距离不唯一，则可将x 归于具有最短距离总体中的任一个，因此，不妨设最短距离唯一）。此时，待判样本x 到总体Gj和Gi的马氏距离的平方差为

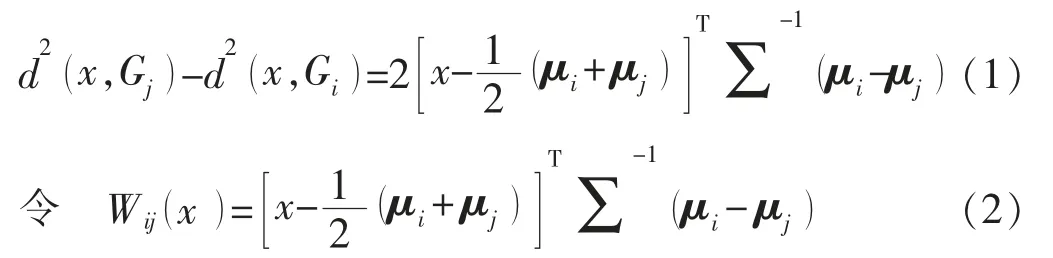
则x 到Gi的距离最小等价于对所有的j≠i，有Wij（x）＞0，从而得到多总体在总体协方差矩阵相等的情况下的距离判别准则为x∈Gi，若对一切j≠i，Wij（x）＞0。

一般情况下，各总体的均值向量μ1，μ2，…，μg及公共协方差矩阵Σ是未知的。对此，可用各总体的训练样本对其作出估计。设x1（k），x2（k），…，xn（k）为来自总体Gk的训练样本（k=1，2，…，g），令

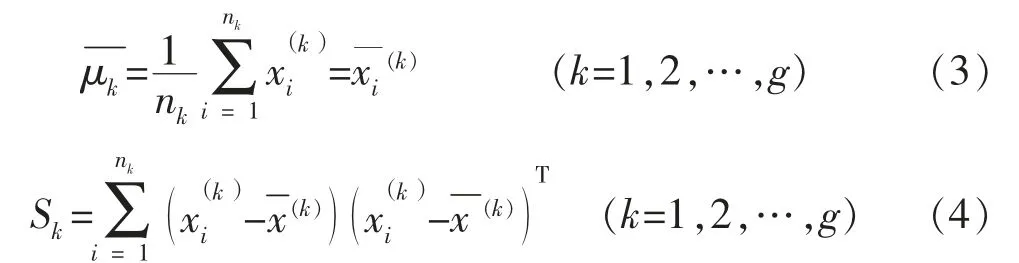
利用Sk（k=1，2，…，g）对Σ的联合估计为

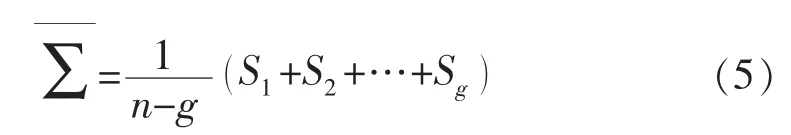
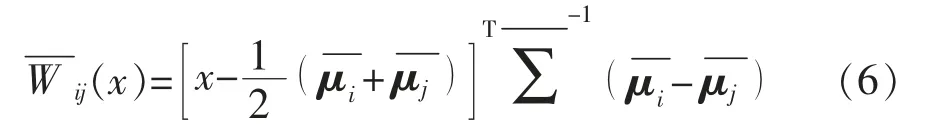
判别准则为x∈Gi，若对一切j≠i，（x）＞0。

1.2 对判别准则的评价

通常用判别准则的误判概率来衡量其优良性，即在一定的判别准则下，将一个样本判错的概率称为该判别准则的误判概率，简称误判率。

当利用各总体的训练样本构造出判别准则后，评估此准则优劣的一个可行性办法，是通过对训练样本中的各样本逐个回判（即将各样本代入判别准则中进行再次判别），利用回判的误判率来衡量判别准则的效果。

具体方法如下：设G1，G2为2 个总体，x1（1），x2（1），…，与x1（2），x2（2），…，xn2（2）分别为来自G1，G2且容量分别为n1和n2的训练样本。以全体训练样本作为n1+n2个新样本，逐个代入已建立的判别准则中判别其归属，这个过程称为回判。回判结果中，n12为G1的样本被错判个数，n21为G2的样本被错判个数，则误判率的回代估计为

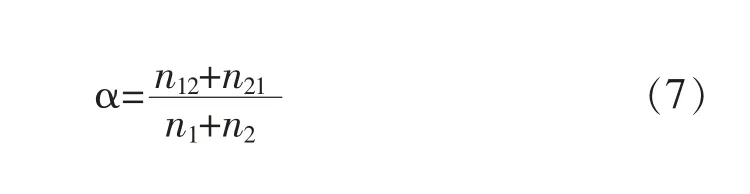
2 煤层压裂选井选层判别方法

2.1 影响煤层气井产气量的参数初选与优选

影响煤层气井压后产气量的参数主要为地质和压裂参数。通过对可能影响煤层气井产气量各参数之间等价、因果及影响过程关系分析，定性确定出地质（补偿密度、补偿中子、井径、微球型聚焦电阻率、深侧向电阻率、浅侧向电阻率、自然电位、自然伽玛、声波时差、煤层深度、煤层厚度）和压裂（前置液量、总液量、加砂量、平均排量）共15 个参数［18-21］。

考虑到可能样本容量比较小且不了解样本分布情况，所以本文采用灰色关联度分析法对参数进行优选。在该方法对样本要求低的条件下对系统因素进行关联分析，有效地弥补了传统的方法（如回归分析、方差分析、主成分分析等方法）对样本要求高的缺陷［22-23］。利用关联度大小的排列顺序，就可以在初选出来的参数中确定影响煤层气井产气量的主要参数。

具体步骤为：1）计算出煤层气井产气量和各影响参数间的关联度；2）按关联度的大小将各影响参数进行排序；3）根据排序结果，确定影响煤层气井产气量的主要参数。

统计山西省某区块125 井层数据，并编写MATLAB计算程序对其进行了灰色关联度分析，最终优选出煤层厚度、补偿密度、微球型聚焦电阻率、井径、浅侧向电阻率、深侧向电阻率、前置液量、总液量、加砂量等共9个主要参数。

2.2 煤层压裂选井选层距离判别分析模型

用统计的125 井层作为训练样本，根据压后效果将样本划分为高、中和低产井层3 类（见表1）。

表1 训练样本类型划分

将灰色关联度分析法优选后得出的9 个参数作为多总体距离判别分析模型的输入变量，分别用x1，x2，…，x9表示，以训练样本中的高、中、低产井层作为判别的总体，分别以G1，G2，G3表示，建立煤层压裂选井选层距离判别模型。在本文中，假定3 个总体的协方差矩阵相等，利用式（1）—（6），编写MATLAB 程序进行计算［24-26］，得到3 个判别函数为

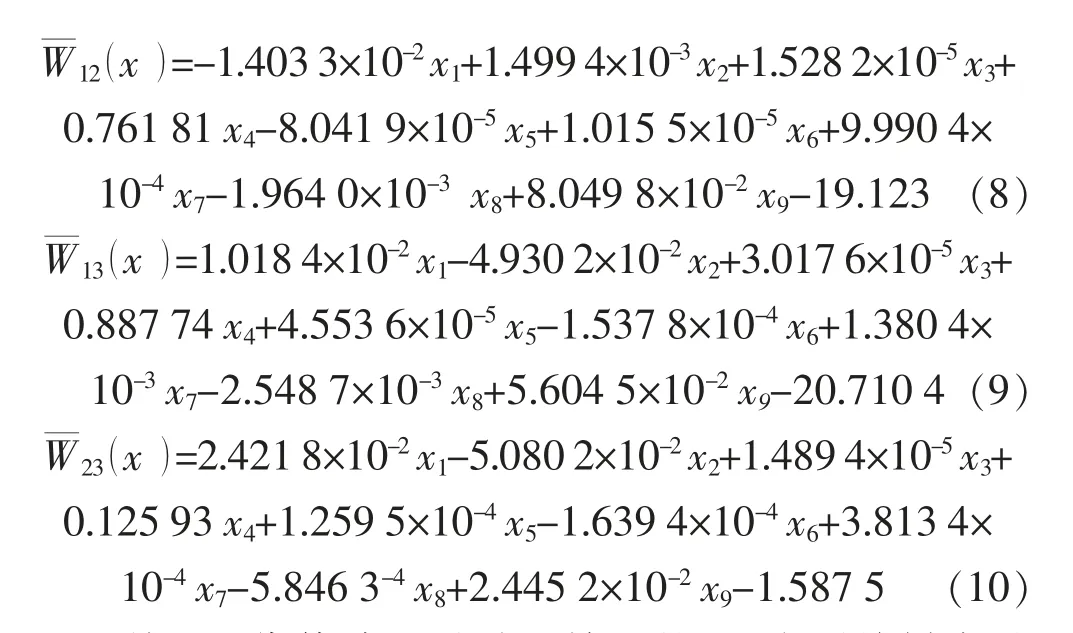
利用回代估计法对随机抽选的25 个训练样本进行判别，判别结果见表2（表中高、中和低产井层分别用数字Ⅰ，Ⅱ，Ⅲ表示）。在判别结果中，只有5 号井C4号层和14 号井C2号层的判别类型与实际不符，误判率仅为8%。

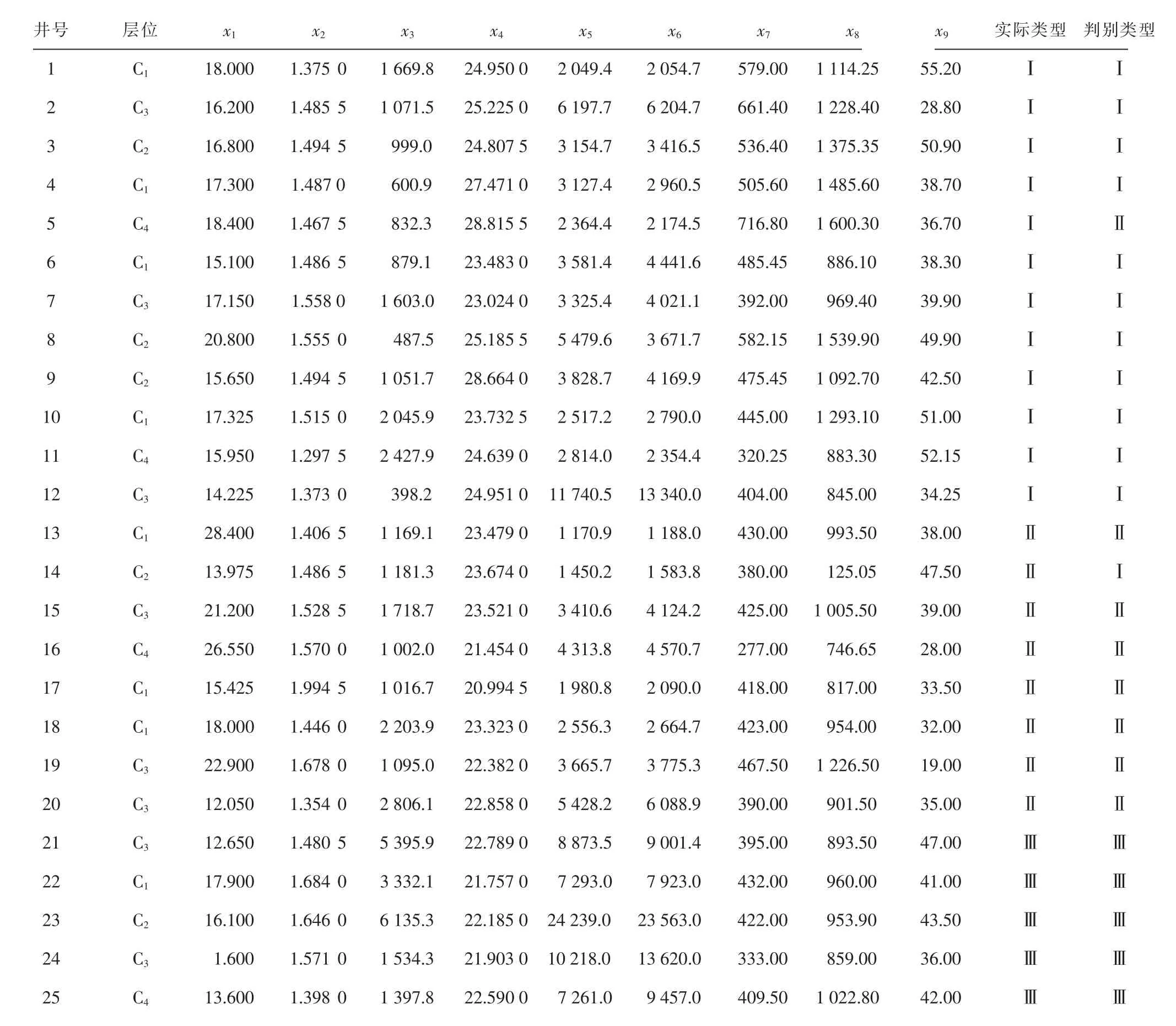
表2 距离判别分析判别结果

3 实例应用

以山西省某区块的2 个井层为例，对煤层气选井选层判别方法的实际应用进行说明。首先收集利用灰色关联度分析法优选出的9 个参数的数据资料，将其处理后得到距离判别函数，输入具体井层参数，得到的判别结果均为高产井层，这与实际压裂后得到的结果一致（见表3）。

表3 实例应用判别结果

4 结束语

煤层压裂选井选层是一个综合考虑各种因素影响的过程，单一使用某种因素得到的选择效果并不理想。本文综合考虑影响煤层气井产气量的主要因素，结合多总体的距离判别分析方法理论，针对山西省某区块建立了煤层压裂选井选层的距离判别分析模型。该模型选用9 个参数作为判别因子，利用已有的煤层气井数据作为训练样本，得出距离判别函数。经回判检验，该判别模型有较高的稳定性和较强的判别能力，回判正确率为92%。通过实例应用，证明了该新方法可以为煤层压裂选井选层提供有效指导。

［1］毕曼，杨映洲，马占国，等.混合压裂在苏里格致密气藏水平井的应用［J］.断块油气田，2014，21（5）：644-647.

［2］刘振宇，刘洋，贺丽艳.人工压裂水平井研究综述［J］.大庆石油学报，2002，26（4）：96-99.

［3］刘长印.不同类型油气井压裂选井选层影响因素分析［J］.油气井测试，2009，18（3）：32-35.

［4］李铁军，薛玲，郭大立，等.基于粗糙集与遗传算法的储层识别技术［J］.断块油气田，2014，21（2）：196-200.

［5］李铁军，贺建，凌立苏，等.油气识别的模糊聚类与遗传神经网络技术［J］.大庆石油地质与开发，2014，33（2）：31-34.

［6］李清.山西延川南煤层气田2 号煤层煤相研究：煤层气开发选区意义［J］.石油实验地质，2014，36（2）：245-248.

［7］鲍云杰.从煤层含气量测定技术发展看页岩含气性评价的发展方向［J］.石油实验地质，2014，36（6）：762-766.

［8］刘长印，孔令飞，朱风阁.探井压前评估技术现状［J］.油气井测试，2003，12（1）：15-16.

［9］宋岩，苏现波，赵孟军，等.中国煤层气成藏地质［M］.北京：科学出版社，2010：1-200.

［10］付永强，郭建春，赵金洲，等.多层次模糊聚类在压裂酸化选井选层中的应用［J］.天然气工业，2001，21（5）：58-60.

［11］吴建发，郭建春，赵金洲，等.模糊分析方法优选压裂井层［J］.天然气工业，2005，25（2）：84-86.

［12］鲁艳峰，赵子丹，李释然，等.西峰油田长8 油藏产能影响因素实验研究［J］.断块油气田，2014，21（6）：779-781.