复值相干模量蚂蚁体技术
2015-06-15史刘秀王静波张如伟黄滨滨
史刘秀,王静波,张如伟,黄滨滨
(1.中国石油大学(北京)地球物理与信息工程学院,北京102249;2.中国石化勘探分公司勘探研究院,四川 成都610041;3.广州海洋地质调查局,广东 广州510760)
0 引言
断层的分布和形态直接影响油气藏的识别和描述,因此精确预测裂缝展布形态对油藏勘探非常重要。传统人工解释方法只能识别较大的断裂系统,难以识别小断层和裂缝。而蚂蚁体技术能够识别常规方法难以识别的微裂缝,得到更精细的断裂系统。
意大利学者Dorigo 于1991年首次了提出蚁群算法[1]。该仿生学算法是通过模拟自然界蚂蚁的觅食行为,集分布式运算、正反馈机制、目的启发为一体的新型随机优化算法。正反馈机制能够快速全局寻优,分布式计算避免算法过早收敛,目的启发可以发现合适的初始搜索路径。同时,Dorigo 应用蚁群算法解决旅行推销员问题(TSP),验证该算法能够迅速提供良好的解决方案。随后10 a 内,Dorigo 等国内外学者不断研究和改进蚁群算法,同时应用蚁群算法解决各类实际问题。2001年,Randen 等人第一次尝试用“电子蚂蚁”识别断层裂缝,详述了电子蚂蚁追踪裂缝的过程,并在SEG年会上发表了相关文章。2002年,Pedersen 等[2]提出蚂蚁体属性,并用蚂蚁体属性预测裂缝分布形态。2009年,Yuan 等[3]建立了一个地球物理多参数反演的改进蚁群算法数学模型,并应用到了地震资料和重力资料反演中。2009年,赵伟[4]提出灰度突变蚂蚁体,并应用于小断层识别。2011年,Aqrawi[5]改进了Sobel 边缘检测算法和倾角扫描算法,并将其与蚁群算法结合进行三维地震资料的断层解释。Sun[6]基于不同频率的地震数据体,应用蚁群算法识别目的层段局部断层和裂缝。严哲[7]提出应用方向约束蚁群算法识别裂缝。2013年,赵俊省[8]改进了方向约束蚁群算法,并将其应用到实际资料的断层解释中。
人工蚂蚁追踪裂缝的过程类似自然蚂蚁觅食的过程:在三维地震数据体中,根据预设条件和概率公式设置电子蚂蚁的起点,断层和裂缝相当于自然蚂蚁的食物,电子蚂蚁追踪断层和裂缝的方法其实就是自然蚂蚁觅食的途径。基于蚁群算法的蚂蚁体作为二次属性能够自动识别、追踪断层和裂缝,提高了断层解释的效率,但是常规蚂蚁体技术基于地震方差体,受地层成层性影响较大,容易产生假象,干扰人们对低角度裂缝和水平断层的识别。本文尝试用多道局部复值相干蚂蚁体属性来预测裂缝,该属性综合了复值相干体和蚂蚁体2 种属性的优点,能够自动识别断裂系统,既消除了地层成层性的影响,又能够压制噪声、提高分辨率,获得较准确的断裂系统的空间分布特征,取得了较好的实际效果。
1 蚂蚁追踪原理
蚂蚁追踪技术是蚁群算法在地震勘探领域中较为成功的应用,能够实现断层和裂缝的自动追踪,缩短三维地震构造解释的周期,提高解释效率。蚂蚁体追踪技术是指在三维地震数据体(地震振幅属性体)中散播大量电子蚂蚁,视三维地震数据体为不同的二维地震数据面,把二维地震数据面划分为不同的网格单元A,作为每只蚂蚁的初始活动边界。在每个网格单元A 中按照一定的概率(断层裂缝等不连续处概率大)放入1 只电子蚂蚁,概率公式为
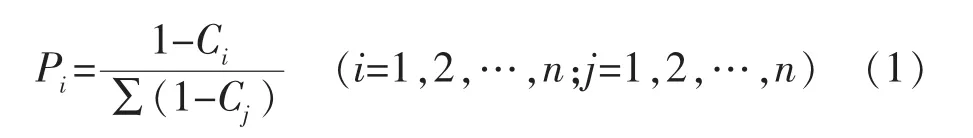
式中:Pi为概率;Ci,Cj分别为归一化后的第i 个和第j个数据点的相干值。
电子蚂蚁的起点确定后,需要确定蚂蚁的追踪方向。把电子蚂蚁的初始活动范围A 划分为更小的区域B,按照一定的算法确定每个小区域B 的主方向。蚂蚁所在数据块B 的主方向即为蚂蚁追踪主方向,蚂蚁运动时允许有一定角度(最大15°)偏离主方向,即蚂蚁追踪背离。每个数据块B 的梯度方向由式(2)得出:
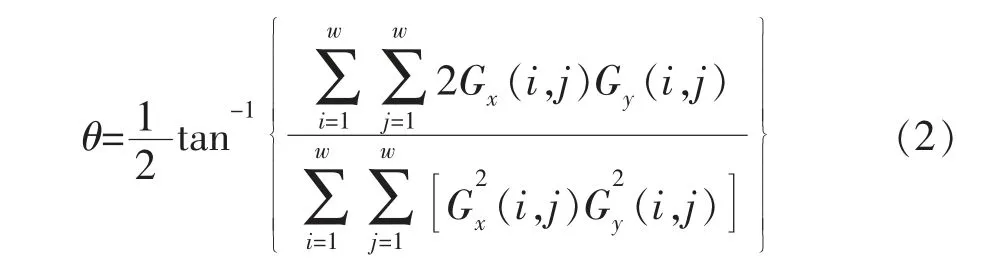
式中:θ 为数据块B 的主方向;Gx(i,j),Gy(i,j)分别为数据块B 中数据点的梯度。
蚂蚁在数据块B 中运动到达的下一个节点,由一定概率公式确定。即在蚂蚁当前搜索范围内,每一个数据点都有信息素浓度,根据一定的算法由数据点的信息素浓度计算数据点的概率。令R 为当前数据点搜索范围内点的集合,蚂蚁运动到下一节点(i,j)的转移概率为
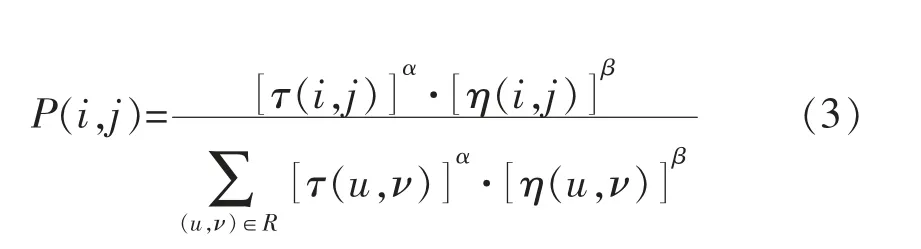
式中:τ(i,j),η(i,j)分别为点(i,j)的信息素与启发信息;α,β 分别为信息素与启发信息的控制因子,控制信息素和启发信息的相对权重。
如果定义启发信息占主导,则β 取相对高值;如果定义信息素占主导,则α 取相对高值。启发信息定义为

式中:C(i,j)为点(i,j)的相干值。
根据式(3)确定该只蚂蚁的目的数据点,也是下一次追踪的起点。蚂蚁在其初始分布范围内,完成一次搜索过程后,每个数据点的信息素会按一定算法更新[7]:
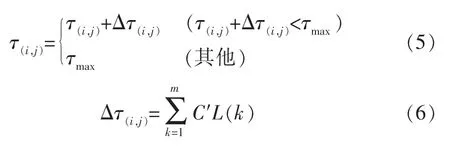
式中:τmax为信息素的上限;Δτ(i,j)为本次循环中数据点(i,j)上信息素的增量[7];m 为本次循环经过此路径蚂蚁的数量;Δτ(i,j)(k)为第k 只蚂蚁在此次循环路径上留下的信息素,取值与蚂蚁搜索的路径长度成正比;C′为信息素更新系数;L(k)为第k 只蚂蚁在此次循环中所搜索路径的长度。
每只蚂蚁沿断裂处进行追踪,并释放信息素以吸引其他蚂蚁,形成正反馈机制,最终完成对整个三维地震数据体的断裂追踪,形成蚂蚁数据体。由于噪声是随机的、无规律的,因此蚂蚁行经该点后遗留的信息素较小,而对于长的、主要的断层线,其信息素较为突出,根据信息素的分布可有效区分边缘和噪声信息,追踪裂缝。利用蚂蚁追踪技术进行断裂系统的预测,将获得一个低噪音、具有清晰断裂痕迹的蚂蚁属性体[9]。
2 蚂蚁追踪参数
2.1 蚂蚁的初始活动边界
蚂蚁初始活动区域的大小决定了一定体积的地震数据体中分布蚂蚁的数量,即蚂蚁分布密度。每只蚂蚁初始活动的区域越大,地震数据体内能够分布的蚂蚁数量越少,蚂蚁密度越小,此时蚂蚁追踪断层的轨迹线越粗糙,只能够识别较大的断裂系统,而忽略了细小的断层;相反,该参数的值越小,地震数据体内分布的蚂蚁总量越多,蚂蚁分布密度越大,越能够识别更小的断层和裂缝。同时,该参数取值的大小直接影响蚂蚁追踪所需的时间,该值越小,蚂蚁追踪所需时间越长。如果研究目标是工区的大断层,其值可以为5~7;如果需要局部地区的精细断裂系统,其值可以为3~4。蚂蚁分布密度越大,蚂蚁追踪微裂缝的能力越强,所需解释时间也越长,因此要根据研究目的设定参数取值。
2.2 蚂蚁轨迹的延展
蚂蚁轨迹的延展是指蚂蚁偏离追踪轨迹的角度,该参数限定了蚂蚁在追踪过程中能够偏离主方向的最大范围。该参数取值越大,蚂蚁追踪过程中与其他蚂蚁能够交流的信息越多,蚂蚁追踪的断层痕迹越合理。最大允许的延展角度为15°,角度越大,越能够解释弯曲断层。对于垂直断层,该参数应取较小值。
2.3 蚂蚁搜索步长
蚂蚁搜索步长是指蚂蚁在追踪过程中每走一步向前搜索的距离,即蚂蚁搜索一个局部最大值所走的距离。该参数取值越大,蚂蚁单次搜索的距离越远,所追踪的断裂越合理,但微裂缝可能会被忽略,一般取3。
2.4 非法步数
如果蚂蚁在一个搜索步长内没有确定一个局部最大值,那么该搜索步长即为一个非法步长,蚂蚁单次追踪过程中,非法步长的数量即为非法步数。非法步数给出了单只蚂蚁在一次追踪过程中允许间断的距离,能够帮助追踪较大的间断性断裂。该参数值越大,蚂蚁搜索的连续性越远,能够识别较大的区域断层。
2.5 合法步数
如果蚂蚁在一个搜索步长内确定一个局部最大值,那么该搜索步长即为一个合法步长,蚂蚁单次追踪过程中,合法步长的数量即为合法步数。合法步数是相对于非法步长而言的,指蚂蚁在非法步长之间允许追踪的合法步长的个数。合法步数越小,断层解释的连续性越强,合法步长越大,断层解释越稀疏,合法步长过大,断裂追踪无实际意义。
2.6 终止标准
终止标准即停止门槛,指蚂蚁追踪全程内允许追踪的非法步长占总步长的比例,常用百分比表示。蚂蚁追踪过程中的非法步长会被累计记录,如果非法步长总数达到终止标准,蚂蚁会结束此次追踪。终止标准值越大,蚂蚁追踪断层的能力越强。
3 复值相干模量蚂蚁体技术
多道局部复值相关算法将传统复值相关算法推广到多道,即用相邻多道加权平均形成模型道代替原始道,然后再利用得到的相邻模型道求相关,替代以往直接利用原始道求复值相关。
二维地震数据的多道局部复值相关计算公式为[10]
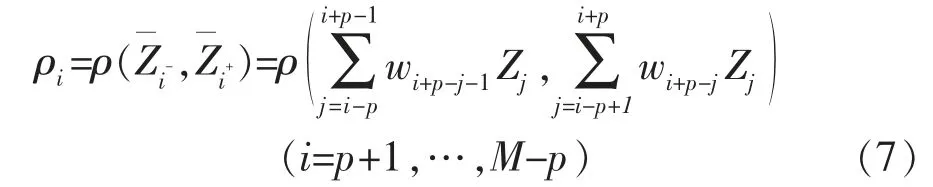
式中:ρi为第i 道位置对应的局部复值相关系数;M 为该二维数据地震道数;算子ρ(·,·)为局部复值相关运算;,分别为第i 道位置处2 个相邻的模型道。

分析局部复值相关算法发现,应用相邻两道直接进行局部复值相关求取的相关系数属性存在边缘异常不突出及抗噪性较弱的问题,进行多道推广后,提高了利用相关系数属性检测地震信息边缘异常和抗噪的能力。本项目将该算法应用于三维地震数据,提取复值相干体。
复值相干模量蚂蚁体技术是基于三维地震数据体提取复值相干属性体,在复值相干体中散播大量“电子蚂蚁”,视三维局部复值相干体为多个不同的二维属性面,把二维属性面划分为不同的网格单元,作为蚂蚁的初始活动边界,在预设断裂条件下,根据概率公式(1)确定蚂蚁的初始位置。当“电子蚂蚁”发现满足预测条件的断裂痕迹时,将追踪断裂痕迹并留下信息素,利用信息素吸引其他“蚂蚁”跟进,形成正反馈机制,直到完成该断裂的识别,而不满足条件的断裂痕迹将不会被追踪。蚂蚁在其活动范围内,完成一次搜索过程后,数据点的信息素按一定算法更新,最终完成对整个三维局部复值相干体的断裂追踪,形成复值相干模量蚂蚁数据体[11-19]。
4 实际资料应用
国内某工区以逆断层为主,工区内主断裂走向为南北向、次断裂走向为东西向。断层和裂缝都是地下介质中非常好的流体流通通道,而且裂缝是致密砂岩储层天然气富集高产的关键。断层发育的地方经常伴随有丰富的裂缝,因此开展断层及大尺度裂缝识别具有重要意义。
笔者对目标层Fd 段提取了复相干属性体、复相干蚂蚁体,并用于解释该目标层段断裂带发育分布规律及裂缝发育的有利区域。作为对比,提取了方差属性体和方差蚂蚁体,并总结出复相干属性体、复相干蚂蚁体在预测裂缝方面的相对优点。研究的主要目标是工区大断层和大尺度裂缝的分布形态,因此蚂蚁的初始活动边界、蚂蚁轨迹的延展、蚂蚁搜索步长、非法步数、合法步数、终止标准各参数分别取值为7,2,3,2,3,5。
图1分别为目标层Fd 底复值相干属性、复相干蚂蚁体属性、方差属性、沿层方差蚂蚁体属性。由图1a和1b 均可清晰看出,目标层主断裂走向为南北向,西北向横切断裂较发育,与工区构造背景相符合。
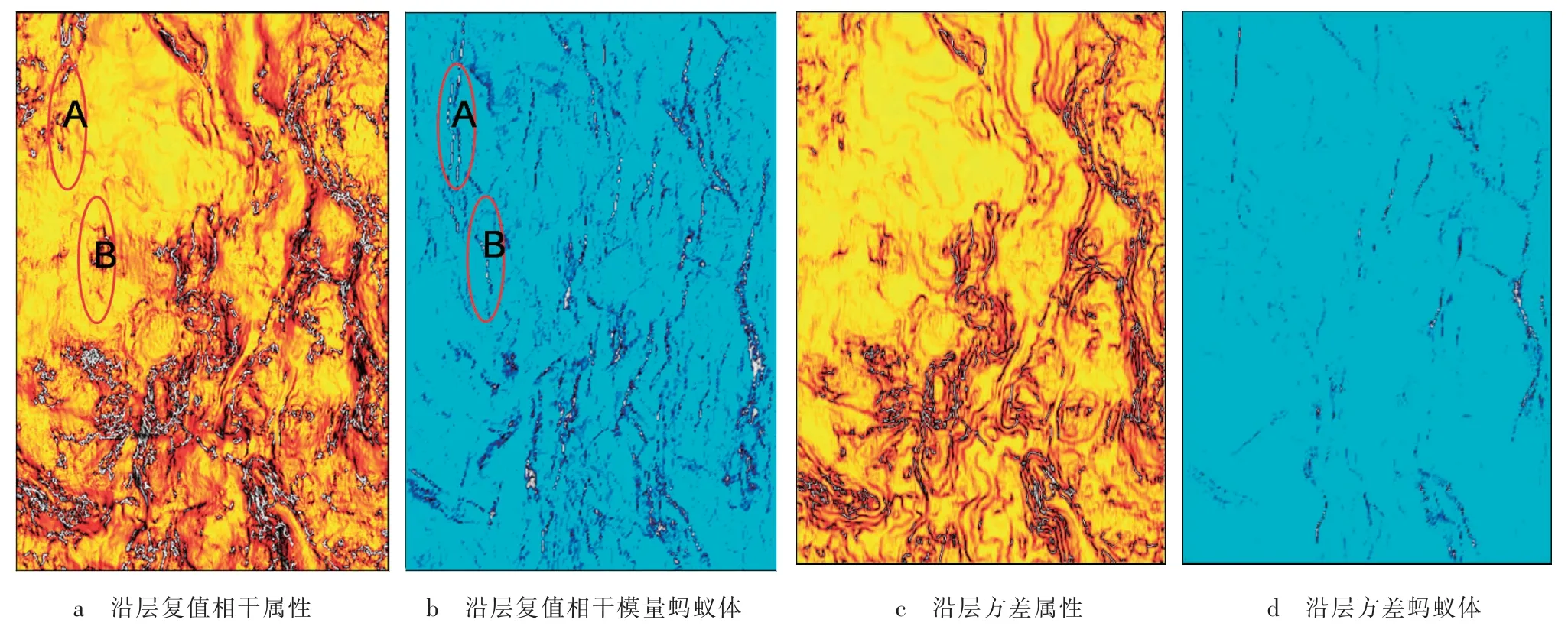
图1 Fd 底叠后属性沿层图
对比图1a和1b,图1b追踪的断层裂缝信息较1a更丰富,刻画更精细,清晰可见小断层、大裂缝。为了验证图1b中的裂缝信息为真,选取了复值相干蚂蚁体属性显示有裂缝而复值相干属性没有显示裂缝的2 个区块,通过属性体横切面与地震原始数据体相应位置纵剖面对比进行验证。
图1a红色椭圆部分没有追踪出裂缝信息,而图1b红色椭圆内追踪出裂缝信息,图2a原始地震剖面目的层段的同相轴明显错开,图2b原始地震剖面目的层段同相轴发生了分叉、 错段,这些证据验证了A,B区块内小裂缝的存在性,由此表明该结果具有较高的准确度和可靠性。
对比图1a和1c,在预测大断层构造走向方面,复值相干属性比方差体属性更清晰;在预测小断层、大裂缝展布方面,复值相干属性可以预测的断层裂缝尺度更小,信息更丰富,分辨率更高。因此,针对目标层段,优选复值相干属性进行断层裂缝预测。
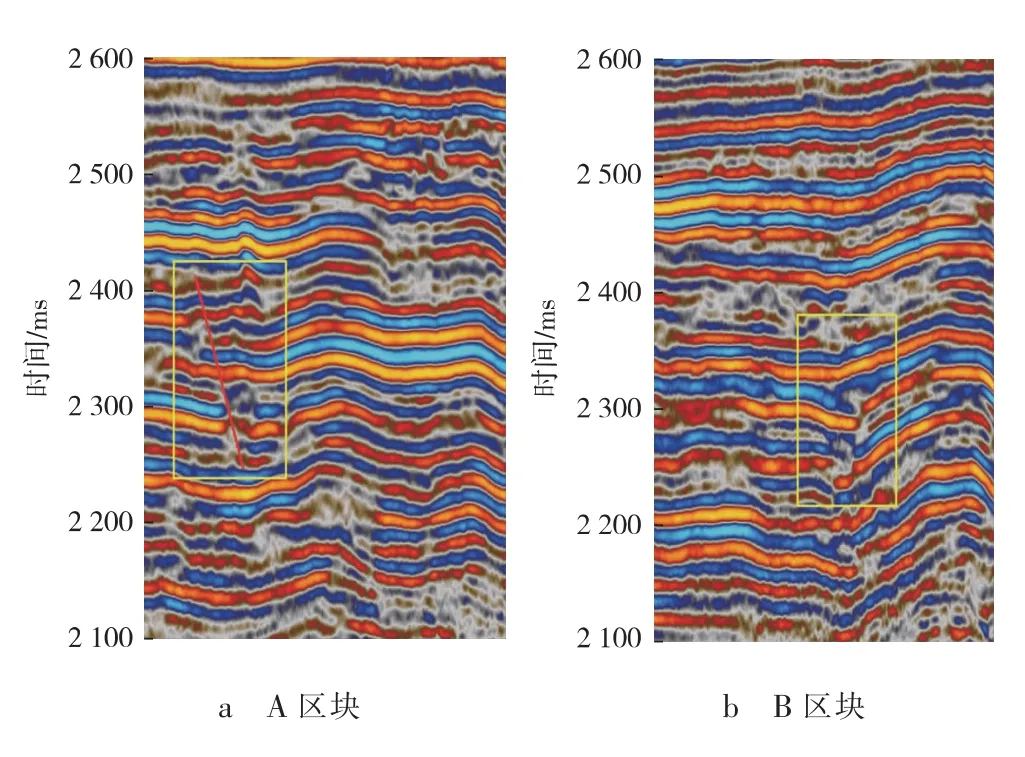
图2 地震纵剖面
对比图1b和1d,复值相干蚂蚁体属性不仅能够清晰预测大断裂走向,主次断裂刻画清晰,而且在预测小断层、裂缝方面也有很好的效果。传统方差蚂蚁体刻画大断裂走向不够清楚,不能识别小断层、大裂缝,分辨率和信噪比较差。因此,针对目标层段目标区块,为了得到更精细的断层裂缝信息,优选复值相干蚂蚁体属性进行预测。
图3为某Crossline 线复值相干蚂蚁体与传统方差蚂蚁体的解释结果,对比图3a和3b可以发现,传统方差蚂蚁体技术受地层成层性干扰较严重,而复值相关蚂蚁体预测裂缝方法消除了地层成层性的干扰,具有较高的信噪比和分辨率。

图3 传统蚂蚁体解释剖面和复值相干蚂蚁体解释剖面对比
5 结论
基于多道局部复值相关的蚂蚁体预测裂缝技术综合了复值相关算法和蚂蚁算法,实现断裂系统自动追踪,缩短了解释周期,提高了裂缝预测效率。通过人工检验原始地震剖面的方法,验证其解释结果具有较高的准确度和可靠性。同时,对比传统方差蚂蚁体技术,该技术解释结果能够消除地层成层性的影响,具有更高的信噪比和分辨率。
[1]Dorigo M,Maniezzo V,Colorni A.Positive feedback as a search strategy[R].Milano:Politecnico di Milano,1991.
[2]Pedersen S I,Randen T,Sunnel L,et al.Automatic 3D fault interpretation by artificial ants [C]// European Association of Geoscientists &Engineers.Florence:64th EAGE Annual Meeting Extended Abstracts,2002:28-34.
[3]Yuan S Y,Wang S X,Tian N.Swarm intelligence optimization and its application in geophysical data inversion [J].Applied Geophysics,2009,6(2):166-174.
[4]赵伟.基于蚂蚁算法的三维地震断层识别方法研究[D].南京:南京理工大学,2009.
[5]Aqrawi A A,Boe H T.Improved fault segmentation using a dip guided and modified 3D Sobel filter[C]//Society of Exploration Geophysicists.San Antonio:SEG Technical Program Expanded Abstracts,2011,30:999-1003.
[6]Sun D S,Ling Y.Application of spectral decomposition and ant tracking to fractured carbonate reservoirs[C]//Society of Exploration Geophysicists.Vienna:73rd EAGE Annual Meeting Extended Abstracts,2011,B035:23-26.
[7]严哲,顾汉明.利用方向约束蚂蚁群算法识别断层[J].石油地球物理勘探,2011,46(4):614-620.
[8]赵俊省,孙赞东.一种改进的蚁群算法在断层自动追踪中的应用[J].科技导报,2013,31(27):59-64.
[9]刘群,李海英,邓光校.地震断裂检测技术在塔河油田南部碳酸盐岩储层及油藏预测中的应用[J].石油与天然气地质,2013,34(2):202-206.
[10]王静波,王尚旭,袁三一,等.利用方向约束蚂蚁群算法识别断层[J].石油地球物理勘探,2014,49(1):190-196.
[11]张淑娟,王延斌,梁星如,等.蚂蚁追踪技术在潜山油藏裂缝预测中的应用[J].断块油气田,2011,18(1):51-54.
[12]李巍,侯吉瑞,丁观世,等.碳酸盐岩缝洞型油藏剩余油类型及影响因素[J].断块油气田,2013,20(4):459-461.
[13]李振华,邱隆伟,齐赞,等.蚂蚁追踪技术在辛KN断块解释中的应用[J].西安石油大学学报:自然科学版,2013,28(2):20-24.
[14]杨瑞召,李洋,庞海玲,等.产状控制蚂蚁体预测微裂缝技术及其应用[J].煤田地质与勘探,2013,41(2):72-75.
[15]林承灏,郭立全,张卫,等.利用蚂蚁追踪技术精细解释矿井地质构造[J].煤炭地质,2013,25(4):55-59.
[16]张磊.蚂蚁体追踪技术在潜西地区构造解释中的运用[J].江汉石油科技,2013,23(3):24-27.
[17]司丽,王彦辉,佟洪海,等.基于地震属性体的三维可视化井震匹配断层解释[J].油气藏评价与开发,2013,3(3):2-4.
[18]巫波,刘遥,容元帅,等.蚂蚁追踪技术在缝洞型油藏裂缝预测中的应用[J].断块油气田,2014,21(4):453-457.
[19]唐琪凌,苏波,王迪,等.蚂蚁算法在断裂系统解释中的应用[J].特种油气藏,2009,16(6):31-33.
