一种基于FPGA的视频几何校正系统设计方案
2015-06-15凌朝东
张 浩,凌朝东*,陈 虎,黄 信,杨 骁,汤 炜,闫 铮
(1.华侨大学 信息科学与工程学院,福建 厦门 361021;2.厦门市专用集成电路系统重点实验室,福建 厦门 361008)
一种基于FPGA的视频几何校正系统设计方案
张 浩1,2,凌朝东1,2*,陈 虎1,2,黄 信1,2,杨 骁1,2,汤 炜1,闫 铮1
(1.华侨大学 信息科学与工程学院,福建 厦门 361021;
2.厦门市专用集成电路系统重点实验室,福建 厦门 361008)
为了满足大视场相关应用、尤其是大屏幕投影拼接技术应用领域对视频图像实时几何校正的要求,本文对视频图像的实时几何校正及其FPGA实现方法进行研究。首先,根据图像几何校正理论基础,利用Matlab等工具进行算法模拟仿真,确定了视频图像实时几何校正系统的基本框架。然后,根据现有的硬件平台DE2的硬件资源情况,细致规划系统结构,并对其中的核心部分几何校正模块进行仿真。最后,通过实际校正测试,断定实验结果达到视频图像实时几何校正的预期效果。实验结果表明:几何校正后,投影仪投射出的图像符合仿真结果,系统延时小于10个时钟周期,远小于毫秒级,且延时恒定,校正误差不超过1个像素。此方案达到了预期视频图像实时几何校正的效果,具有相当的借鉴、参考意义。
大视场;投影拼接技术;几何校正;FPGA
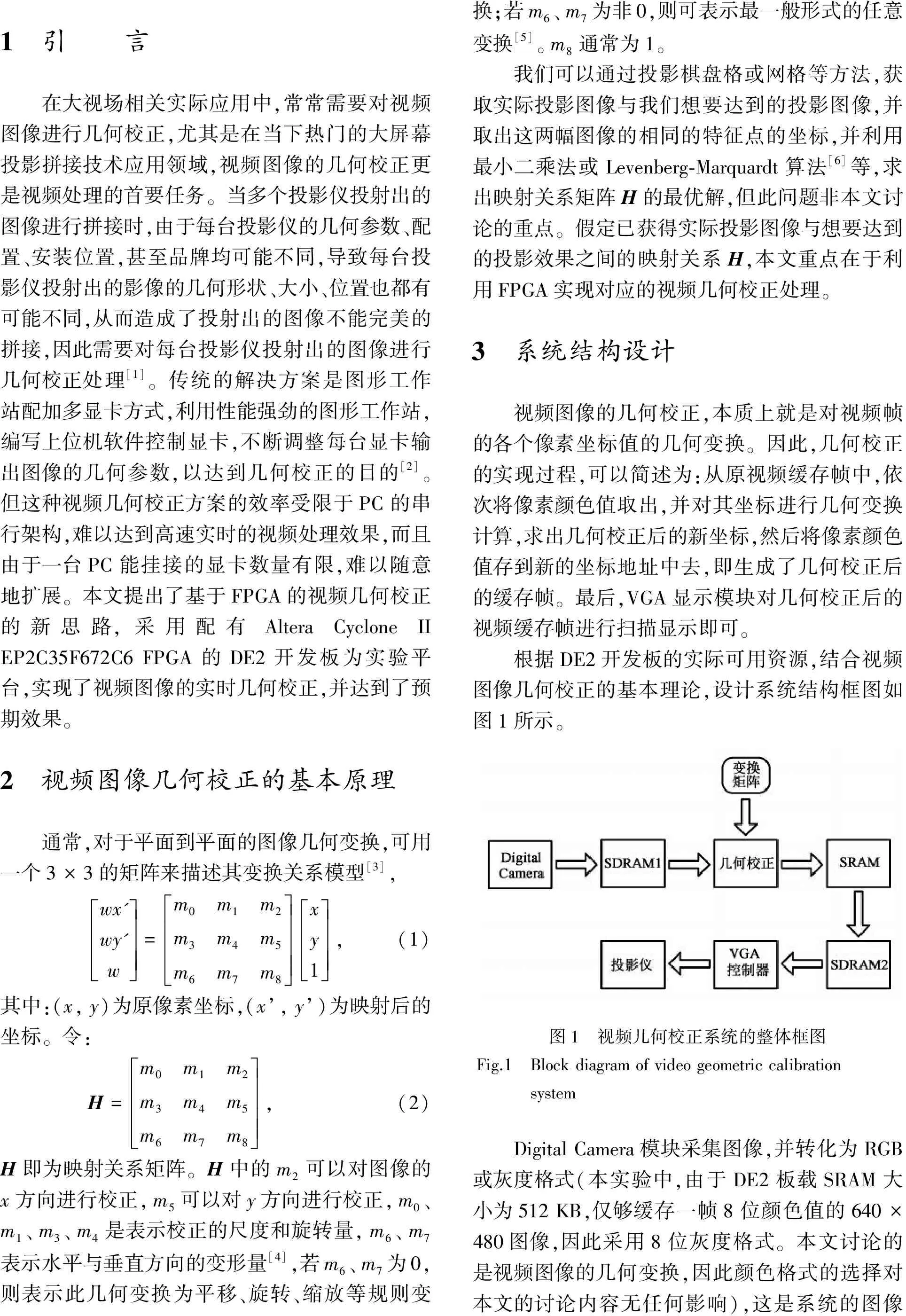
1 引 言 在大视场相关实际应用中,常常需要对视频图像进行几何校正,尤其是在当下热门的大屏幕投影拼接技术应用领域,视频图像的几何校正更是视频处理的首要任务。当多个投影仪投射出的图像进行拼接时,由于每台投影仪的几何参数、配置、安装位置,甚至品牌均可能不同,导致每台投影仪投射出的影像的几何形状、大小、位置也都有可能不同,从而造成了投射出的图像不能完美的拼接,因此需要对每台投影仪投射出的图像进行几何校正处理[1]。传统的解决方案是图形工作站配加多显卡方式,利用性能强劲的图形工作站,编写上位机软件控制显卡,不断调整每台显卡输出图像的几何参数,以达到几何校正的目的[2]。但这种视频几何校正方案的效率受限于PC的串行架构,难以达到高速实时的视频处理效果,而且由于一台PC能挂接的显卡数量有限,难以随意地扩展。本文提出了基于FPGA的视频几何校正的新思路,采用配有AlteraCycloneIIEP2C35F672C6FPGA的DE2开发板为实验平台,实现了视频图像的实时几何校正,并达到了预期效果。2 视频图像几何校正的基本原理通常,对于平面到平面的图像几何变换,可用一个3×3的矩阵来描述其变换关系模型[3], wx'wy'wéëêêêêùûúúúú=m0m1m2m3m4m5m6m7m8éëêêêêùûúúúúxy1éëêêêêùûúúúú,(1)其中:(x,y)为原像素坐标,(x’,y’)为映射后的坐标。令: H=m0m1m2m3m4m5m6m7m8éëêêêêùûúúúú,(2)H即为映射关系矩阵。H中的m2可以对图像的x方向进行校正,m5可以对y方向进行校正,m0、m1、m3、m4是表示校正的尺度和旋转量,m6、m7表示水平与垂直方向的变形量[4],若m6、m7为0,则表示此几何变换为平移、旋转、缩放等规则变换;若m6、m7为非0,则可表示最一般形式的任意变换[5]。m8通常为1。我们可以通过投影棋盘格或网格等方法,获取实际投影图像与我们想要达到的投影图像,并取出这两幅图像的相同的特征点的坐标,并利用最小二乘法或Levenberg⁃Marquardt算法[6]等,求出映射关系矩阵H的最优解,但此问题非本文讨论的重点。假定已获得实际投影图像与想要达到的投影效果之间的映射关系H,本文重点在于利用FPGA实现对应的视频几何校正处理。3 系统结构设计视频图像的几何校正,本质上就是对视频帧的各个像素坐标值的几何变换。因此,几何校正的实现过程,可以简述为:从原视频缓存帧中,依次将像素颜色值取出,并对其坐标进行几何变换计算,求出几何校正后的新坐标,然后将像素颜色值存到新的坐标地址中去,即生成了几何校正后的缓存帧。最后,VGA显示模块对几何校正后的视频缓存帧进行扫描显示即可。根据DE2开发板的实际可用资源,结合视频图像几何校正的基本理论,设计系统结构框图如图1所示。图1 视频几何校正系统的整体框图Fig.1 BlockdiagramofvideogeometriccalibrationsystemDigitalCamera模块采集图像,并转化为RGB或灰度格式(本实验中,由于DE2板载SRAM大小为512KB,仅够缓存一帧8位颜色值的640×480图像,因此采用8位灰度格式。本文讨论的是视频图像的几何变换,因此颜色格式的选择对本文的讨论内容无任何影响),这是系统的图像
图3 矩阵运算器模块原理图
Fig.3 Schematic diagram of matrix operation module
4.3 矩阵运算器模块的波形仿真
我们设定要将视频图像在x方向缩小2倍,并向右平移100个像素;在y方向也缩小2倍,并向下平移200个像素;视频图像形状不变。易知,映射矩阵应为:

按照表1的输入参数格式,将H变化为:

将此参数输入仿真文件,得到仿真结果如图4所示。由图4以及设定的仿真条件可知,图4中坐标(500,400)对应的输出坐标为(350,400),(600,10)对应的输出坐标为(400,205),其他依次类推,均符合预期的校正结果。由图4还可知,矩阵运算模块造成的时钟延时约为7个时钟周期。由于本设计系统中,所有模块的同步时钟均采用VGA的像素时钟,即摄像头将图像帧数据存入SDRAM1时,几何校正模块也在同时工作,将SDRAM1的数据取出进行几何校正,且校正速度与VGA扫描速度一致,因此整个系统的视频几何校正部分的延时就是这7个时钟周期。已知分辨率640×480的视频的像素时钟频率约为25 MHz[9],则7个时钟周期的延时时间小于1 μs,远小于毫秒级。而对常见的60帧/s的视频,每帧时间约为1/60 s,可见本系统的视频几何校正部分的延时远小于视频每帧的显示时间,因此不会对人的视觉观感产生任何影响。

图4 矩阵运算器模块波形仿真图Fig.4 Waveform of matrix operation module simulation
5 实验结果与分析
5.1 视频几何校正结果分析
实验分两步进行。第一步为:首先,投影仪正对幕布,投射出完美的特征影像并拍照记录,作为几何校正目标投影影像。然后,将投影仪摆放任意角度,投射出不完美的不规则形状的特征影像,保持投影仪位置固定并拍照,获得目前实际投影影像。最后,利用Matlab等工具获取实际影像到目标影像的映射关系矩阵H。第二步为:将第一步获得的映射关系矩阵H输入到FPGA中,FPGA将依据H对摄像头采集的视频进行几何校正,并经由第一步中固定位置的投影仪投射到幕布上,对比目标影像,观察是否达到预期效果。实验器材见表2,具体过程如下。

表2 实验器材列表Tab.2 List of the experimental equipment

图5 目标投影效果与未几何校正投影效果对比图Fig.5 Comparison of target projection result and non geometric calibration projection result
目标投影效果与未经几何校正的实际投影效果对比如图5所示。
利用Matlab将目标投影效果图与实际投影效果图的特征点坐标进行提取,考虑相机失真因素,并用最小二乘法计算得到实际投影效果与目标投影效果的映射关系矩阵为[10]:

按照表1将H转化为

然后将H导入FPGA中,得到几何校正结果如图6所示。
图6(a)是用液晶显示器显示的原始视频图像。将其直接用投影仪投射在屏幕上的显示效果如图6(c)。将6(a)进行映射关系矩阵为H的几何校正之后,得到视频图像图6(b),图6(b)看似发生了不规则的变形,但将其通过投影仪投射到屏幕上时,实际投影效果如图6(d),将图6(d)与目标投影效果图5(a)对比发现,投射出的影像的几何失真得到校正,可判定实验达到了预期的视频几何校正效果,从而肯定了本方案的正确性与可行性。理论上,根据Hx的不同,本设计可以对视频图像做任何形状的几何校正。
而针对多投影系统的视频图像几何校正,实现方法与本实验相同:只需先设定一个多投影拼接后的目标效果图,然后将此图中每台投影仪各自分工的部分,与对应投影仪的实际投影效果进行比对分

图6 几何校正结果对比图Fig.6 Comparison of geometric calibration results
析,获得映射关系矩阵Hx(每台投影仪对应的映射关系矩阵可能是不同的)。再根据Hx对每台投影仪的视频输入源做不同参数的几何校正即可。
5.2 几何校正精度分析
对于本文所述的视频图像几何校正方案,误差来源主要有两点:一是Hx的参数误差,主要包括相机鱼眼效应引起的误差、Hx参数求解时迭代计算次数有限所引起的误差、解出的参数由于四舍五入引起的误差等,这部分误差是由仪器设备、上位机算法等共同造成,非本文讨论重点。二是本设计方案的系统误差,在本设计中,由于iX、iY、oX、oY均为小于103的整数,而Hx均保留到小数点后4位,根据式(5)、式(6)可知坐标变换过程中FPGA进行相关矩阵运算的误差最大不超过1个像素点,不会对显示效果产生任何影响。若资源足够,增加Hx的小数保留位数,则几何校正的精度将更高。
5.3 资源使用情况分析
实际资源占用情况如图7所示。

图7 FPGA的资源占用情况Fig.7 Use of FPGA resources
由图7可知,对于DE2开发平台板载的EP2C-35F672C6 FPGA,经Quartus II综合后本方案几何校正部分各项硬件资源占用率均不超过30%,可见本方案具有资源占用率少、效率高的优势,因此适合工程应用。
6 结 论
本文依据大视场应用、尤其是大屏幕投影拼接技术领域对视频图像几何校正快速、稳定、适宜推广的需求,设计了一套基于FPGA的视频图像几何校正方案。本文首先介绍了视频图像几何校正的基本理论。然后据此设计了几何校正的系统结构。之后根据DE2开发平台的实际资源,详细设计了几何校正模块的具体结构并进行了仿真。最后,通过观察实际的投影校正效果,验证了本方案的可行性。实验结果证明:本方案系统延时小于10个时钟周期,远远不到毫秒级,且延时恒定不变,几何校正误差最大不超过1个像素,对人的视觉观感不会有任何影响。而且本方案资源占用率低,适合大范围应用。虽然由于DE2平台资源所限,未能进行更高分辨率的视频几何校正测试,但本方案的设计思想仍然具有相当的借鉴、参考意义。
[1] 王胜正, 杨杰. 自动多投影仪非线性几何校正与图像边缘融合方法[J]. 上海交通大学学报, 2008, 42(4): 574-578. Wang S Z, Yang J. Auto-nonlinear geometry calibration and edge blending of multi-projector display system [J].JournalofShanghaiJiaotongUniversity, 2008, 42(4): 574-578. (in Chinese)
[2] 李斌. 低成本多投影仪拼接方法研究[D]. 济南:山东大学,2005. Li B. Study on Low-cost multi-projector mosaic [D]. Jinan: Shandong University, 2005. (in Chinese)
[3] 张德丰. MATLAB数字图像处理[M]. 北京:机械工业出版社,2009. Zhang D F.DigitalImageProcessingwithMATLAB[M]. Beijing: China Machine Press, 2009. (in Chinese)
[4] 张铮,王艳平,薛桂香. 数字图像处理与机器视觉[M]. 北京:人民邮电出版社,2010. Zhang Z, Wang Y P, Xue G X.DigitalImageProcessingandMachineVision[M]. Beijing: Ports & Telecom Press, 2010. (in Chinese)
[5] 陶婷婷,张亚萍. 多投影显示系统的几何校正及边缘融合技术研究与实现[J]. 云南师范大学学报,2014,34(1): 54-60. Tao T T, Zhang Y P. Research andrealization of geometric calibration and edge blending for multi-projector display system [J].JournalofYunnanNormalUniversity, 2014, 34(1): 54-60. (in Chinese)
[6] 刘淑. 多通道大屏幕图像无缝拼接技术研究[D]. 北京:北京交通大学,2011. Liu S. Theresearch on multi-projectors large format mosaic [D]. Beijing: Beijing Jiaotong University, 2011. (in Chinese)
[7] Integrated Silicon Solution, Inc. IS61LV25616_Datasheet.pdf [OL]. www.issi.com, 2001.
[8] 叶茂. 多屏投影显示系统的自动校正技术[D]. 成都:四川大学,计算机应用,2006. YE M. Automaticcalibration techniques for multi-projector display systems [D]. Chengdu: Sichuan University, 2006. (in Chinese)
[9] Video Electronics Standards Association. VESA and industry standards and guidelines for computer display monitor timing (DMT) [EB]. 2004.
[10] 蔡山,张浩,陈洪辉,等. 基于最小二乘法的分段三次曲线拟合方法研究[J]. 科学技术与工程,2007, 7(3): 352-355. Cai S, Zhang H, Chen H H,etal. Research of piecewise cubic-fitting method based on least-square principle [J].ScienceTechnologyandEngineering, 2007, 7(3): 352-355. (in Chinese)
Design of video geometric calibration system based on FPGA
ZHANG Hao1,2, LING Chao-dong1,2*, CHEN Hu1,2, HUANG Xin1,2, YANG Xiao1,2, TANG Wei1, YAN Zheng1
(1.InstituteofInformationScienceandEngineering,HuaQiaoUniversity,Xiamen361021,China;2.KeyLaboratoryofASICandSystemofXiamen,Xiamen361008,China)
In order to realize the real-time video image geometric calibration in large field of view image applications, especially in large format projection mosaic technique field, this paper analyzes the video image geometric calibration and its realization based on FPGA. First, according to the basic theory of image geometric calibration, this paper describes the simulation of algorithms with Matlab and other tools, and designs the basic frame of the video image geometric calibration system. Then, the system structure is detailed designed based on the hardware resources of DE2 platform and the geometric calibration module is simulated. Finally, based on the actual calibration test, this paper concludes that the experimental results achieve the desired target of real-time video image geometric calibration. Experimental results show that the image which has been calibrated and projected by projector is consistent with the simulation results. The delay of system is less than 10 clock cycles, far less than millisecond level, and the value of delay time is a constant. The inaccuracy of the calibration system is no more than one pixel. This design achieves the desired target of real-time video geometric calibration, which has considerable significance for reference.
large field of view; projection mosaic technique; geometric calibration; FPGA
张 飙(1969-),男,四川人,硕士,主要从事LED显示技术、激光雷达技术的研究。E-mail:75990383@qq.com 周国清(1965-),男,江西人,博士,教授,博士生导师,主要从事遥感技术的研究。E-mail:glitezhou@yahoo.com
2014-10-14;
2014-11-06.
国家自然科学基金(No.61203369,No.61204122); 福建省自然科学基金(No.2011J01351); 福建省科技计划重点项目(No.2013H0029) ;泉州市科技计划项目(No.2013Z33)
1007-2780(2015)03-0459-08
TN911.73
A
10.3788/YJYXS20153003.0459
*通信联系人,E-mail:edac@hqu.edu.cn
