利用组合广义Harmonic小波设计梳状滤波器
2015-06-15樊新海张传清江鹏程梁瑞刚
樊新海, 张传清, 江鹏程, 梁瑞刚
(装甲兵工程学院机械工程系,北京 100072)
利用组合广义Harmonic小波设计梳状滤波器
樊新海, 张传清, 江鹏程, 梁瑞刚
(装甲兵工程学院机械工程系,北京 100072)
在机械振动信号处理中常出现多倍频谐波谱特征或多边带调制谱特征,为更好地提取或去除这些特征频率,需要设计性能优良的梳状滤波器。根据Harmonic小波的特点,给出了利用组合广义Harmonic小波设计梳状滤波器的详细步骤和应用实例。研究结果表明:增大滤波器的阶数和使用旁瓣小的窗函数可以提高梳状滤波器的性能。
故障诊断;信号处理;广义谐波小波;梳状滤波器
在机械故障诊断和技术状况评估中,实测振动信号中常会出现以某频率为基频的多倍频谐波谱特征,或以载频为中心、以故障特征频率为间隔的多边带调制谱特征。通过设计性能优良的梳状滤波器,可以较好地提取或去除这些特征频率[1]。
Harmonic小波常用于谐波小波变换,在信号处理中取得了良好的应用效果[2-3]。为了扩展Harmonic小波在其他方面的应用,本文研究了基于组合广义Harmonic小波的梳状滤波器设计方法,并给出了具体实现步骤,通过对某型坦克传动箱振动速度信号进行处理验证了该滤波器性能。
1 理论基础
1.1 Harmonic小波
1993年,英国剑桥大学Newland教授[4]成功构造出了在频域紧支、具有“盒形”频谱特征的谐波小波(Harmonic Wavelet),如图1所示。
设频域实偶函数Ψe(Ω)为
(1)
频域虚奇函数Ψo(Ω)为
(2)
利用Ψe(Ω)和Ψo(Ω)构造出谐波小波的频谱Ψ(Ω)为
Ψ(Ω)=Ψe(Ω)+jΨo(Ω)=

(3)
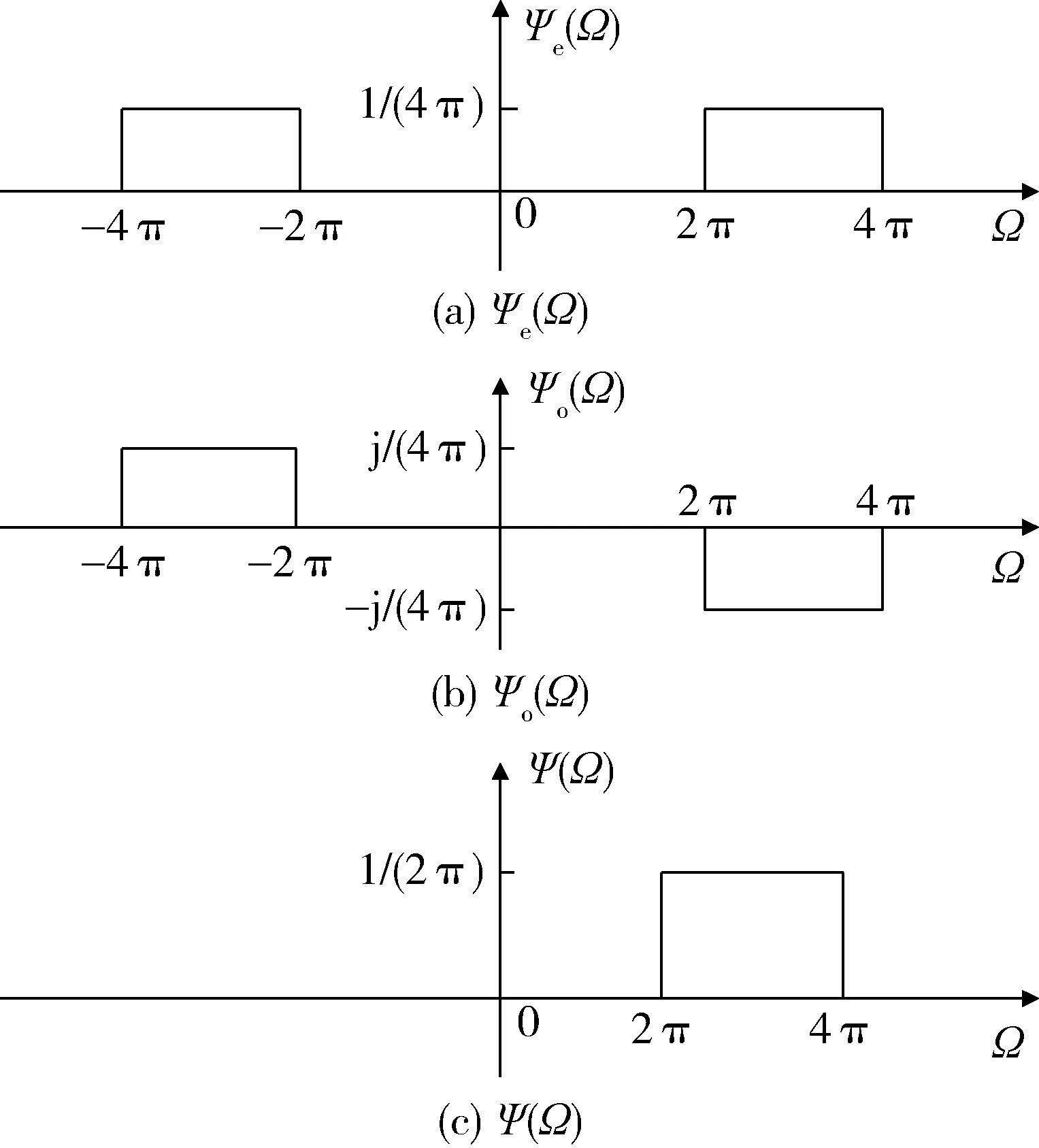
图1 Ψe(Ω)、Ψo(Ω)和Ψ(Ω)的波形
将傅里叶变换对中的1/(2π)因子放在正变换中,对式(1)、(2)进行傅里叶逆变换,得到谐波小波时域表达式为

(4)
实部ψe(t)和虚部ψo(t)的波形分别如图2、3所示,其表达式分别为
(5)
(6)
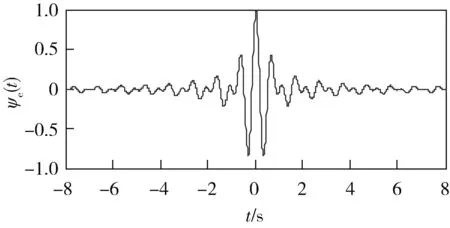
图2 谐波小波的实部波形

图3 谐波小波的虚部波形
从图1-3不难发现Harmonic小波的特点:
1) 从频域上看,Harmonic小波具有“盒形”特征,Ψe(Ω)为实偶函数,Ψo(Ω)为虚奇函数,且Ψo(Ω)=-jsgn(Ω)Ψe(Ω),Ψ(Ω)只有正频率成分;
2) 从时域上看,ψe(t)是实偶函数,ψo(t)是实奇函数,以1/t衰减速率从中心向两边衰减,不是紧支撑的;
3) 实部ψe(t)的Hilbert变换是虚部ψo(t),ψ(t)满足解析小波的定义,因此Harmonic小波是复解析小波。
事实上,由Heisenberg测不准原理可知:时域和频域都具有严格紧支性的小波函数是不存在的。因此,在实际应用中,由于时域截断,谐波小波会在频域产生严重的Gibbs现象。
1.2 广义Harmonic小波
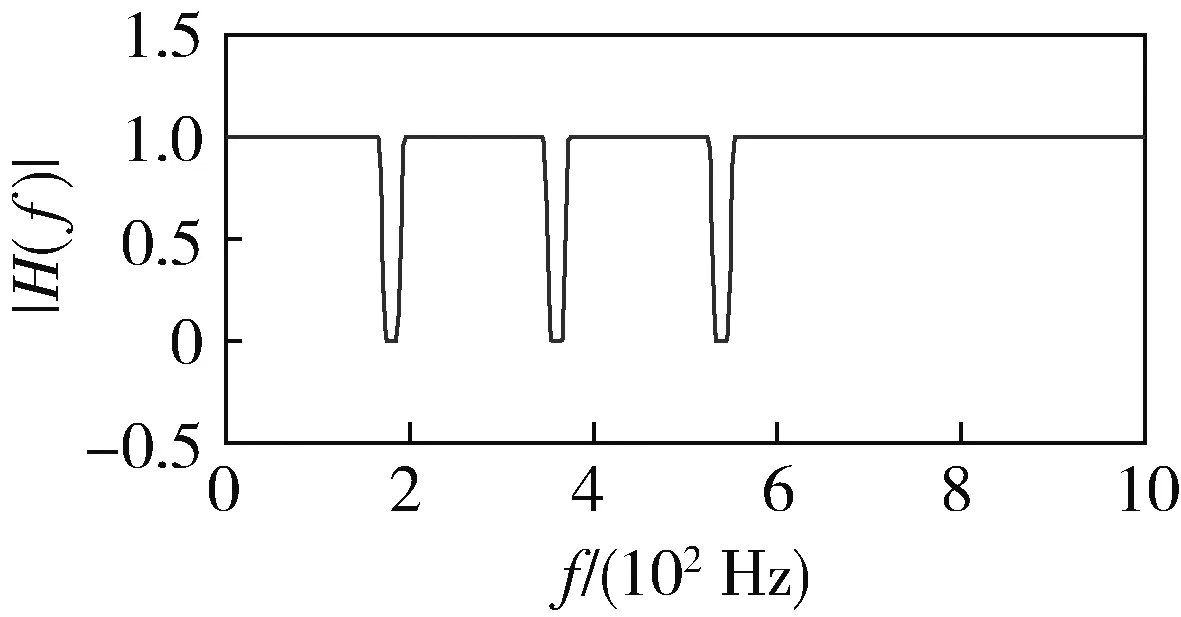
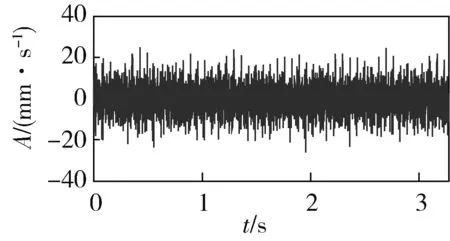
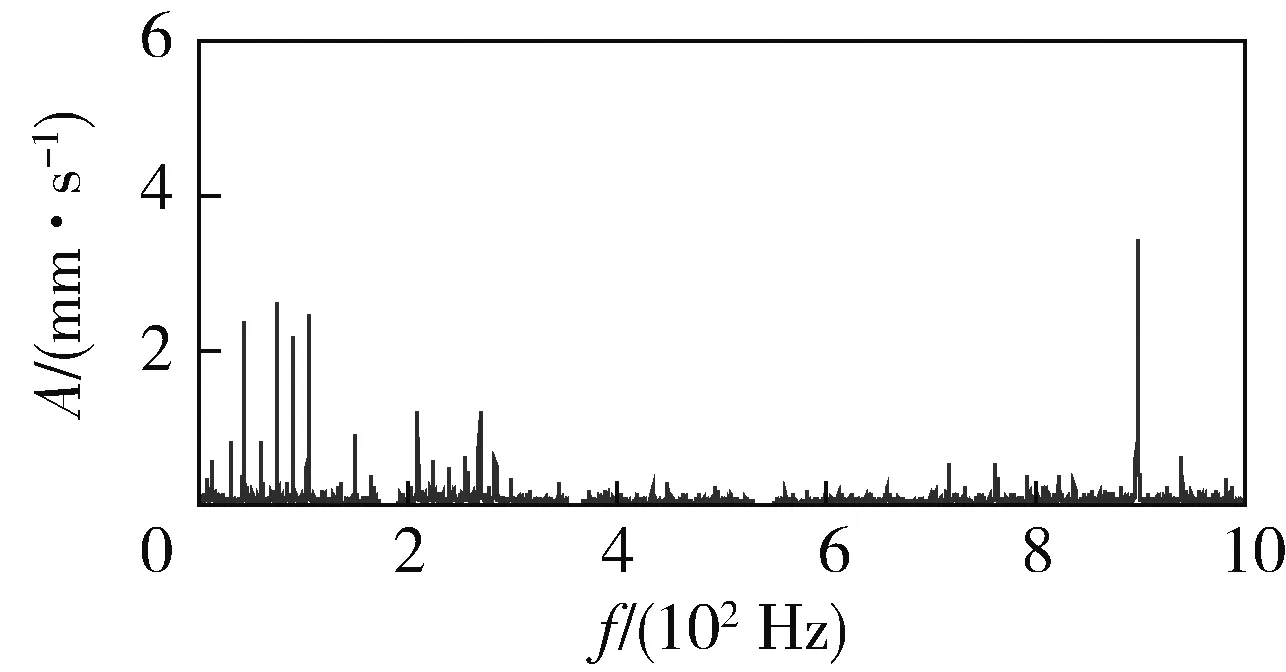
1994年,Newland将谐波小波推广到广义谐波小波[5]。设正实数m,n∈R+,且m (7) 其时域表达式为 (8) 与谐波小波相比,广义谐波小波使得通带的选择更加灵活,通过改变m和n的取值,就可以改变频带的中心频率和带宽,从而增加了该小波的适用性[6]。 1.3 组合广义Harmonic小波 由于广义谐波小波具有分析频带的中心频率和带宽选取灵活的优点,通过给定一系列合适的mi,ni(i=1,2,…,k)值,就可以方便地构建出组合广义谐波小波,使其幅频曲线具有梳状谱特征,从而实现梳状滤波器的功能。组合广义Harmonic小波的频域和时域表达式分别为 (9) (10) 为了减小Gibbs现象,可在时域加旁瓣较小的窗函数,如Hamming窗,也可鉴于在Morlet小波中,高斯函数因子决定了时域曲线的衰减特性,在组合广义Harmonic小波中引入高斯函数因子,从而提高时域衰减速率,消除频域过渡带附近的振荡。 3) 计算组合广义谐波小波的实部和虚部:当n=1,2,…,N时,有 当n=0时,利用洛必达法则求得 当n=-N,-N+1,…,-1时,由xR(n)=xR(-n),xI(n)=-xI(-n)得到。 4) 加窗:选定旁瓣较小的窗函数d(n),令xR(n)=xR(n)d(n),xI(n)=xI(n)d(n)。 5) 移位:xR(n)和xI(n)为非因果序列,向右平移N,记hR(n)=xR(n-N),hI(n)=xI(n-N),n=0,1,…,2N,使得hR(n)和hI(n)为因果序列,最终得到所设计滤波器的系数。 按上述方法,取fs=2 kHz,半阶数N=100,通带个数k=4,各通带的下截止频率fL=100, 300, 500, 700 Hz,上截止频率fH=200, 400, 600, 800 Hz,在不加窗和加Hamming窗2种情况下,梳状滤波器的幅频特性曲线对比如图4所示,其实部hR(n)的波形分别如图5、6所示。 对比图4-6可见:不加窗时,梳状滤波器的Gibbs现象较为严重;加Hamming窗后,梳状滤波器系数的衰减速率加速,时域紧支性提高,而频域振荡基本消除。因此,通过增大滤波器的阶数和加旁瓣较小的窗函数,可以提高梳状滤波器的性能。 图4 加窗前后梳状滤波器的幅频特性曲线对比 图5 不加窗梳状滤波器的实部波形 图6 加Hamming窗梳状滤波器的实部波形 坦克作为一种高机动性陆战装备,实现其不解体检测诊断和技术状况评估难度较大。为了消除行驶过程中坦克动力传动系统振动特性受油门、负载、路面起伏等的影响,提高测试信号的平稳性,测试工况选在原位停止、断开两侧履带条件下进行。图7为某型坦克传动箱在发动机转速为1 800 r/min、变速箱挂1挡时振动速度信号的时域波形,相应的幅值谱如图8所示。 图7 传动箱振动速度信号的时域波形 图8 传动箱振动速度信号的幅值谱 该传动箱为二级增速装置,输入轴通过弹性联轴器与柴油机曲轴相联,输入轴齿轮齿数为30。当柴油机转速为1 800 r/min时,曲轴和传动箱输入轴的转频为30 Hz,传动箱内齿轮啮合频率为900 Hz,即图8中谱线b对应的频率。 坦克动力传动装置安装在车体动力舱内,组成一个整体。柴油机工作时各缸爆发产生的振动对传动箱、变速箱也会产生较大影响。根据12缸柴油机的工作特点,当其转速为1 800 r/min时,汽缸的爆发频率为180 Hz,图8中谱线a1、a2、a3对应的频率为180、360、540 Hz,分别为柴油机爆发频率的基频、2倍频和3倍频。 如果通过直接计算图8所示信号的振动烈度对传动箱技术状况进行评估,振值就会偏大,因此应该将柴油机汽缸爆发振动的影响去除。利用前文给出的方法设计一梳状陷波滤波器,其幅频特性曲线如图9所示。利用该滤波器对图7所示信号进行滤波,滤波后振动速度信号的时域波形如图10所示,相应的幅值谱如图11所示。 图9 梳状陷波滤波器的幅频特性曲线 图10 滤波后振动速度信号的时域波形 图11 滤波后振动速度信号的幅值谱 对比图8、11可见:滤波后柴油机汽缸爆发频率及其2、3倍频得到有效去除,振动烈度值由原来的7.59 mm/s减小到6.42 mm/s。 Harmonic小波从频域特征入手构造小波函数,易于理解,但在实际应用中需要在频域特征的理想性与时域衰减的快速性之间进行折中。利用组合广义Harmonic小波设计的梳状滤波器是一种解析滤波器,既能够实现线性相位,又有利于滤波后通频带信号的包络提取,将滤波过程与Hilbert变换一并实现。通过增大滤波器的阶数和对滤波器系数加旁瓣较小的窗函数,有助于减小过渡带的宽度、消除频域振荡,从而提高滤波器的性能。 [1] 赵俊龙,郭正刚,张志新,等.梳状滤波器在滚动轴承早期故障诊断中应用[J].振动与冲击,2008,27(12):171-174. [2] 张文斌,周晓军,林勇,等.基于谐波小波包方法的旋转机械故障信号处理[J].振动与冲击,2009,28(3):87-89. [3] 王志刚,李友荣,吕勇.基于谐波小波变换的共振解调法[J].振动与冲击,2006,25(4):159-161. [4] Newland D E. Harmonic Wavelet Analysis [J]. Proceedings of the Royal Society of London, 1993, 443(10): 203-225. [5] Newland D E. Wavelet Analysis of Vibration-part2: Wavelet Maps [J].Journal of Vibration and Acoustics, 1994, 116(4):417-425. [6] 陈果.一种改进的谐波小波及其在转子故障诊断中的应用[J].机械工程学报,2011,47(1):8-16. (责任编辑:尚彩娟) Design of Comb Filter by Using Combined Generalized Harmonic Wavelet FAN Xin-hai, ZHANG Chuan-qing, JIANG Peng-cheng, LIANG Rui-gang (Department of Mechanical Engineering, Academy of Armored Force Engineering, Beijing 100072, China) Because multi-harmonic spectrum feature or multi-sideband modulated spectrum feature is often appeared in mechanical vibration signal processing, comb filer with excellent performance is needed to extract or remove these characteristic frequencies. According to the characteristics of harmonic wavelet, the detailed steps and the applied example of comb filter design are brought forward using combined generalized harmonic wavelet. The result shows that the performance of comb filer can be improved by increasing the order of filter and using window function with small side lobe. fault diagnosis; signal processing; generalized harmonic wavelet; comb filter 1672-1497(2015)01-0071-04 2014- 08- 25 樊新海(1973-),男,副教授,博士。 TN713+.7 A 10.3969/j.issn.1672-1497.2015.01.014
2 设计步骤



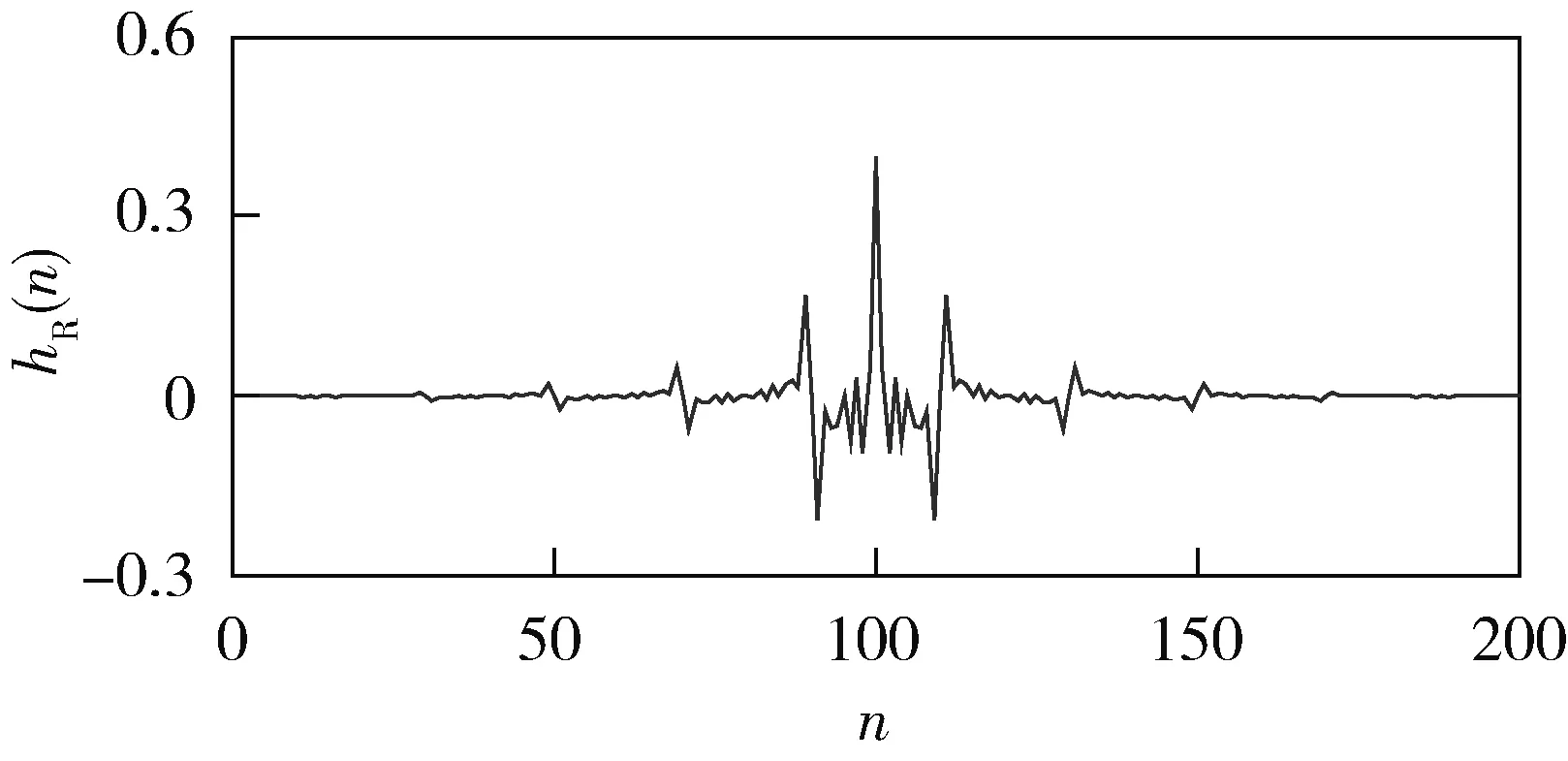
3 实例应用

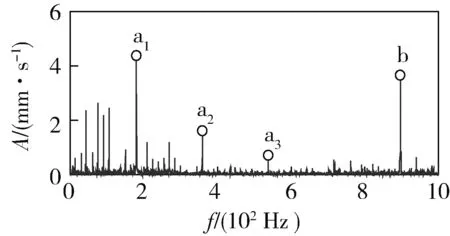
4 结论
