道路约束条件下的地面运动目标跟踪*
2015-06-15贺丰收缪礼锋
贺丰收,缪礼锋,张 莹
(中航工业雷达与电子设备研究院,江苏 无锡 214063)
道路约束条件下的地面运动目标跟踪*
贺丰收,缪礼锋,张 莹
(中航工业雷达与电子设备研究院,江苏 无锡 214063)
有效使用道路信息能显著提高地面运动目标跟踪性能。基于卡尔曼滤波理论,提出了道路约束条件下的滤波方法。首先建立了描述道路网中路段的数学模型,给出了将目标分配于道路的定位算法;然后推导了道路约束条件下的过程噪声矩阵;提出了路段切换时状态修正公式;在道路约束最大后验概率估计准则下,根据道路参数修正状态与协方差。蒙特卡洛仿真结果证明了该算法的优越性能,且定量分析表明其计算量是可接受的。
地面运动目标,跟踪,道路约束,卡尔曼滤波
0 引言
近年来,由于军事和民用需求的发展,地面动目标跟踪得到了更多的关注。地面目标跟踪受到环境限制,较空中目标跟踪更为困难[1]。但地面目标跟踪可利用公路网络、地形特征等非正态信息提高跟踪质量。Blackman明确指出[2]:“地面动目标跟踪的关键在于使用道路网络,有效地使用道路网络是提高地面目标跟踪性能最重要的途径”。
国内外学者就地面目标跟踪开展了大量研究,见文献[3-8]。这些文献都没有给出道路建模的细节,且默认目标一直在道路上运行即忽略了目标至道路的分配算法;没有考虑目标穿过道路节点时的状态修正处理,对约束滤波算法的计算复杂度也没有进行分析。本文根据道路约束的特点,重点研究道路约束条件下的滤波方法。
1 道路约束描述
1.1 运动与测量模型
考虑到地面目标一般只在二维平面上运动且机动相对较小,故用二维匀速模型对目标进行建模,系统动态方程和测量方程的表达形式为:
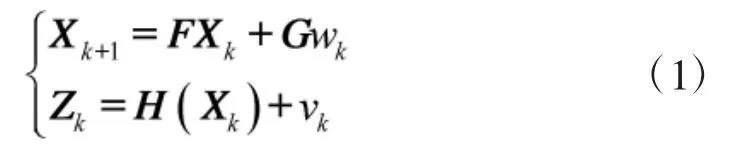
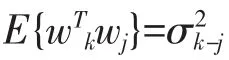

相应地vk=[vRvAz]T,其标准差为σR、σAz。
1.2 路段建模
首先对地面空间进行定义,一般的地面空间分成两大部分,开放区域与道路网。其中开放区域跟空中状态一样,对目标运动模型没有限制;而位于道路网的目标运动只会沿道路平行方向,因此,运动的预测与滤波模型受到道路网的约束。用起始点、结束点与宽度联合表示路段。连接的起始点和结束点称之为交叉点。弯曲的道路线可采用多个小的相邻路段近似。如图1所示:

图1 路段示意图
目标时刻k的状态变量在开放区域可以表示为:
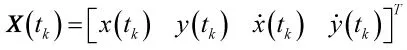
把目标的状态约束到其所在的道路段s时,约束后的状态变量可以表示为:
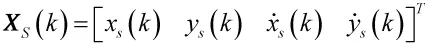
设定某一道路段的两个起始点和结束点分别为(x1,y1)和(x2,y2),则当目标处在道路段上,以下两个条件必须同时满足:
1.2.1 目标位置处在两条端点连线上
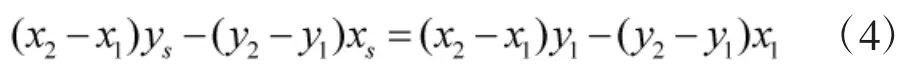
1.2.2 速度和道路段方向平行
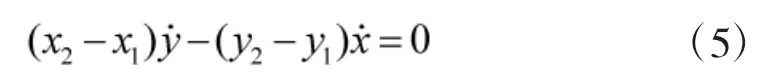
因此,这种约束可以表示为:
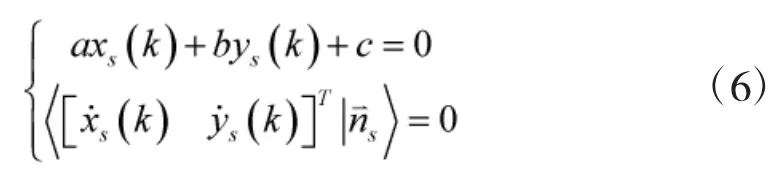
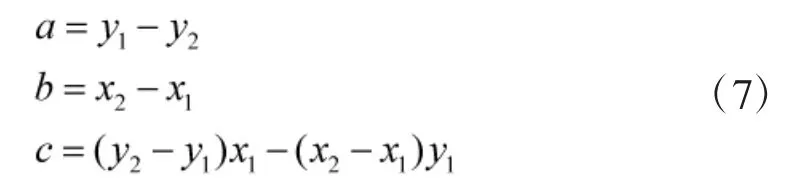
若采用矩阵的概念则可以表示成
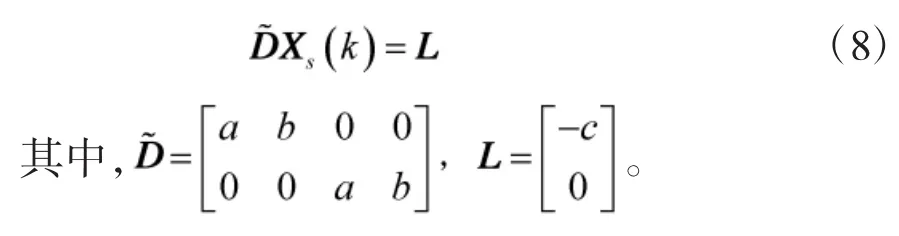
道路与地理坐标系x轴夹角为θs(见下页图2),其计算公式为:

1.3 路段分配
得到路段参数的前提是确定目标所在的路段,需要将正确的路段分配给目标。道路分配问题的实质即判决目标是否位于某一道路段上。构造假设检验:
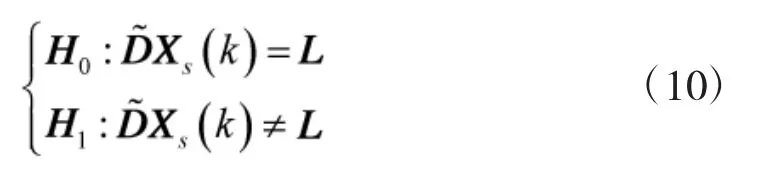
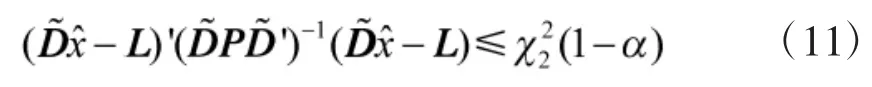
如上式成立,则接受假设H0。门限χ22(1-α)是服从两个自由度的卡方分布,其置信度为100(1-α)。如果存在多个道路段均满足以上不等式,则将目标分配到马氏统计距离(不等式左侧)最小的道路段上。
需要注意的是,一般在航迹起始之后一段时间再进行路段初始分配。在地面运动目标航迹起始之后,如果目标的状态估计协方差满足设定的门限条件,即可将目标分配在道路段上。如果协方差较大,则状态估计还不稳定,带有较大误差,过早地启动道路分配可能会导致错误的结果。一旦确定目标所在道路段,则不必重复进行路段分配,根据路段连接关系即可得到确定新的路段。在复杂道路条件下,如交叉、汇合、分支等复杂道路情况,可通过多假设方法[9]或者变结构多模型[10]方法判断所处的新路段。
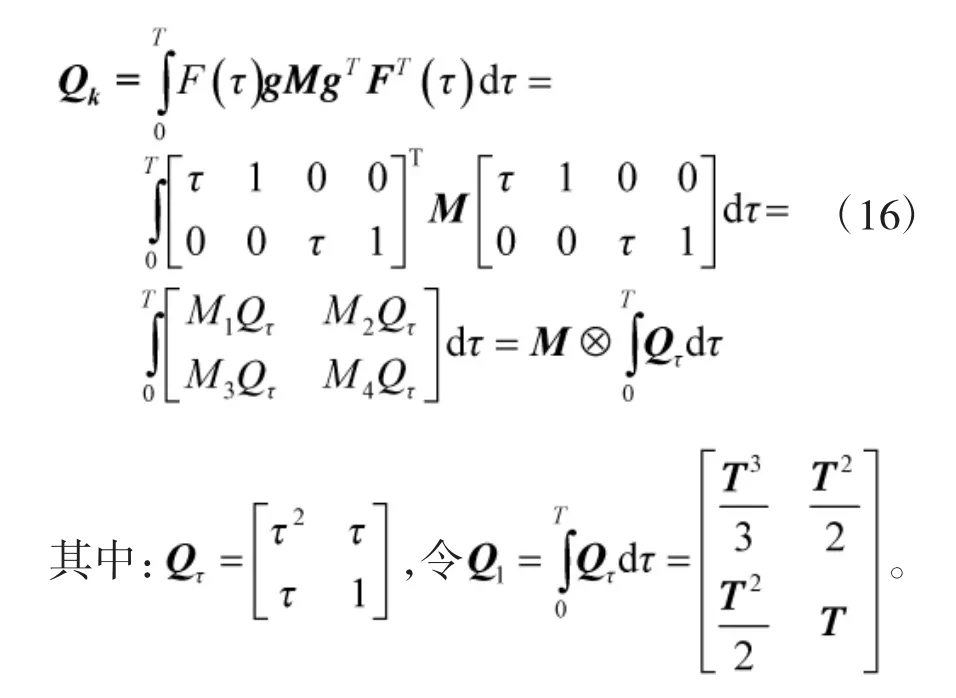
2 道路约束滤波
2.1 道路约束下的过程噪声
在对开放空间目标进行滤波时,由于状态不受约束,所以过程噪声在平面上的X,Y向可以认为是大致相等的。但是对于处于道路网的地面目标而言,其状态是受约束的,其过程噪声应该充分考虑当前状态的特点。
行驶在道路上的目标一般会在道路上,顺着道路方向前进。换句说话其垂直于道路方向的过程噪声不会很大,其标准差一般不会大于道路宽度的一半;而顺着道路方向的过程噪声一般不受影响。
可得:
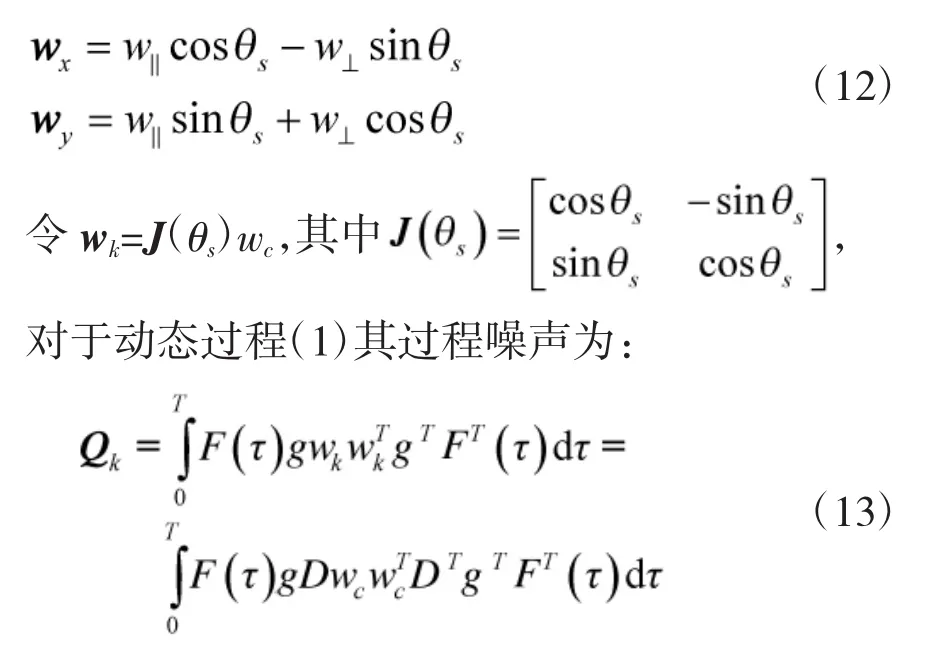
令:
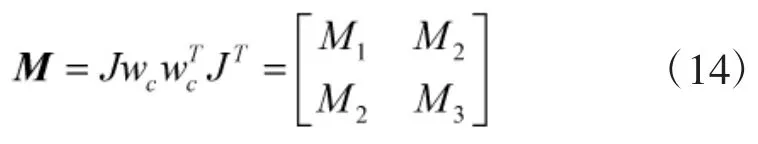
其中,
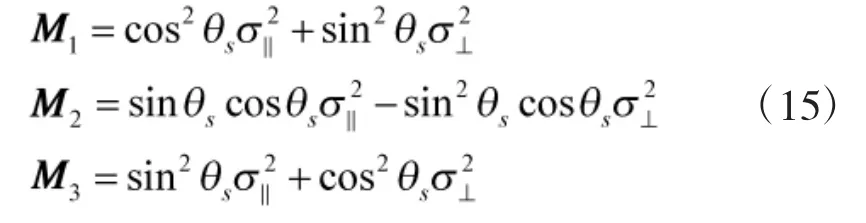
且与无关。
故根据式(13)可得:
可得到:

展开后得:
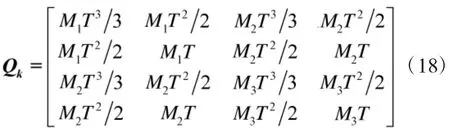
引入道路约束后,垂直于道路方向上的过程噪声分量方差在减小,减小的程度由W/σT2决定,W为道路宽度。当 W=σT2时,σ⊥2=0.291 1σ2,当W=3σT2时,σ⊥2=0.973 4σ2,即当W≥3σT2时,道路宽度对过程噪声的影响几乎可以忽略。在目标进入宽度为W=σT2的道路时,与没有道路约束过程噪声的概率密度函数如图2所示:
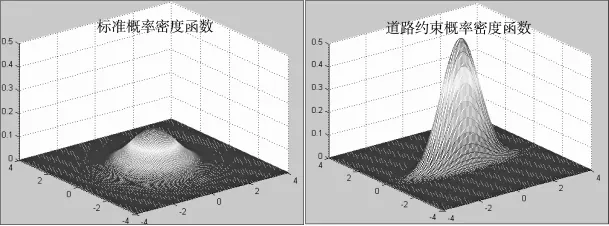
图2 过程噪声概率密度函数对比图
2.2 路段切换修正
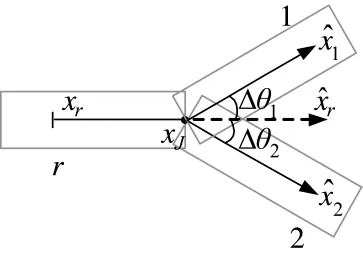
图3 路段切换预测示意图
道路段长度是有限的,因此,在目标运动所在路段r运动至路段i时,如果按照路段r的信息外推,则会出现如图3所示的外推值x^r,严重影响外推精度。在式(24)所示的协方差矩阵修正后,协方差矩阵显著缩小,较大的预测误差将会导致目标测量值不能落入关联波门内,导致航迹中断。因此,需要修正相应的滤波状态至对应的路段。如图3所示。
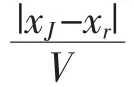
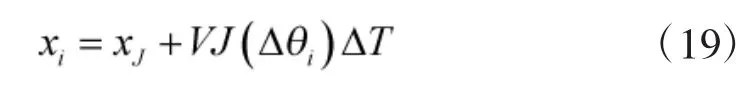
其中,
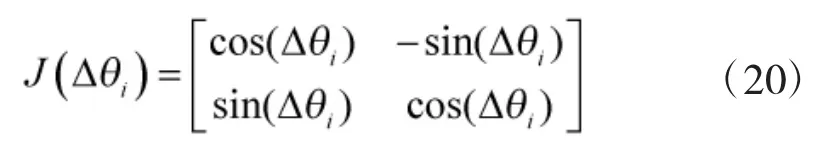
△θi为路段i与原路段r的夹角。
2.3 估计修正方法
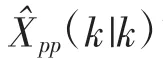
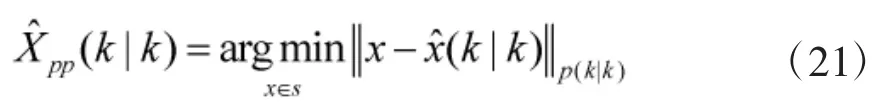
状态修正需要将目标投影在道路上,可基于马氏距离最小化来获得这个状态投影。为了获得在道路段上的速度方向,需要引入速度方向和标准道路段矢量的正交关系。根据式(8)所示的限制关系,在道路限制条件下的最小化问题可以表述为:
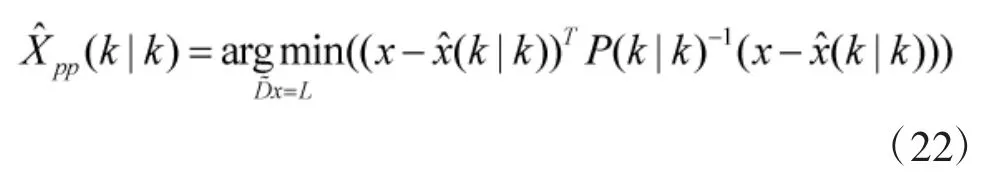
根据拉格朗日方法和状态约束理论,道路约束条件下的最大后验概率状态估计和协方差估计为:

其中Id为单位矩阵,而
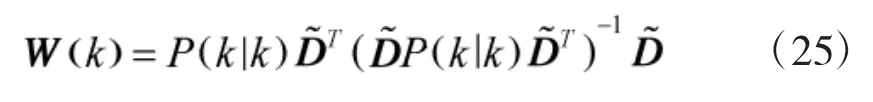
3 仿真与分析
3.1 仿真场景描述
为了评估上述算法的性能,考察道路约束条件对滤波精度的影响,构造一个单目标跟踪道路交通网络图。目标以20 m/s的速度在道路上做匀速运动,道路宽度统一设为5 m。
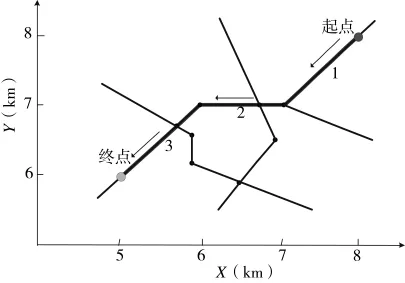
图4 仿真道路交通网示意图
目标途经的道路与节点参数如表1所示:
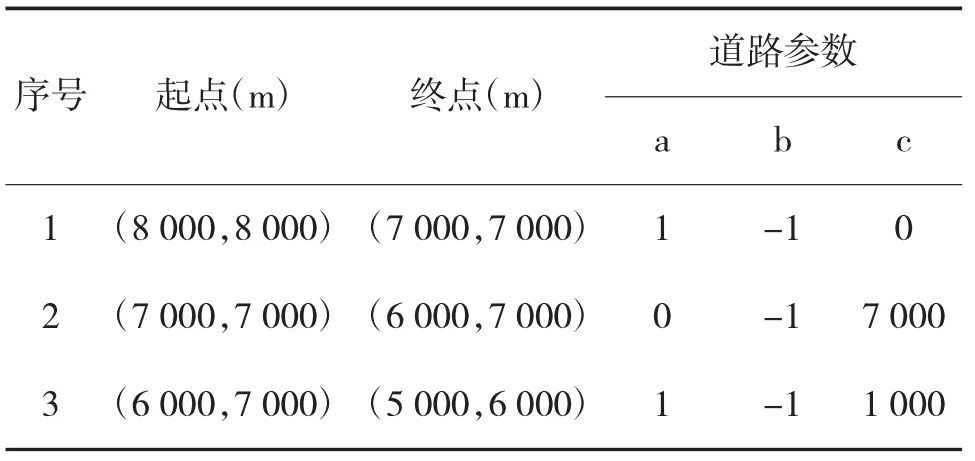
表1 道路参数表
雷达位于坐标原点,采样周期为5 s。对地慢动目标探测一般采用低重频,不提供径向速度测量(或有严重模糊的径向速度测量),距离量测噪声标准差σR和方位角量测噪声标准差σAz分别为30 m和8 mrad。道路宽度W为5 m,在采样周期为5 s时,取策动噪声系数为σ=0.2。为重点说明本文研究滤波算法性能,在本仿真场景中,不考虑地形遮挡影响,道路节点分支采用MHT方法[9-11]处理,本文不再赘述。蒙特卡洛仿真次数取500次。
3.2 仿真结果
分为4种情况进行比较:①不引入任何约束条件进行标准扩展卡尔曼滤波(EKF),作为基准参考值;②过程噪声约束(Noise Constrain)卡尔曼滤波方法,垂直道路方向的过程噪声取值为平行于道路方向过程噪声的0.01;③采用估计修正(Estimation Modification)卡尔曼滤波方法,同时对滤波的状态和协方差每个采样周期进行一次修正;④同时采用过程噪声约束和状态修正的道路约束(Road Constrain)卡尔曼滤波方法。通过比较这4种方法的性能表现,评价本文提出方法对滤波性能的影响。其中,后三种方法都采用了道路切换修正方法。
从仿真结果来看,EKF方法在目标真实轨迹附近有明显的波动,而道路约束的RCKF方法目标的真实轨迹吻合的非常好,准确地定位在道路中心线上。下面的精度图清楚地表明了道路约束方法在位置精度和速度精度上的巨大优势。
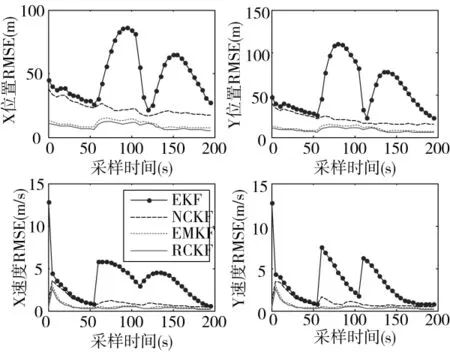
图5 4种方法的跟踪精度比较图
由图5可以看出,引入道路约束对跟踪性能有明显的提高,但不同的方法对性能的改善也是不一样的。采用过程噪声约束的NC方法可以大大的提高跟踪的精度,尤其是在目标受道路限制,运动方向发生突变时,采用过程噪声约束的方法可以非常平滑地过渡至新的运动状态,没有出现大的误差尖峰;而采用状态修正的EM方法性能提高更为明显,误差水平更低;同时结合了过程噪声约束与估计修正的RCKF方法精度最高。估计修正的EMKF方法优于噪声约束方法,其原因是估计修正方法不但可以改变协方差矩阵,而且可以直接修正目标的位置和速度,结果反应更加快速,更加准确。RCKF相较于EMKF的性能提高有限,主要是因为EMKF方法性能已经很好,NC方法在此基础上的改进余地不大。另外,路段切换修正对精度的影响也是很重要的。道路约束的滤波方法必须结合路段切换修正,才能取得较好的效果。
为了定量比较道路约束方法带来的性能变化,以EKF方法作为基准衡量另外三种道路约束方法。精度改善的详细数据见表2所示:
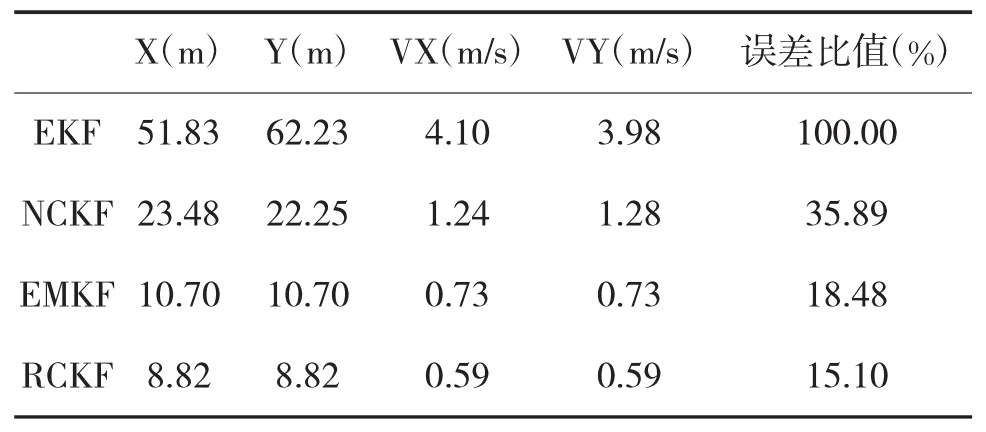
表2 精度和误差比值表
3.3 计算量分析
根据标准卡尔曼滤波公式[12],统计得到标准卡尔曼滤波器总的计算量为:
3n3+2n2m+2nm2+nm+n2次乘加运算,以及一个m×m维的矩阵求逆。其中,m为测量维数,n为状态维数。文献[13]指出,逆矩阵计算量与同阶矩阵相乘计算量相当,为m3次乘法与加法,因此,标准卡尔曼滤波总的计算量为:
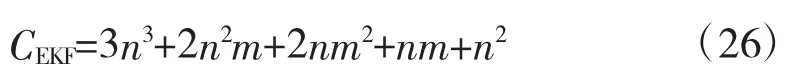
过程噪声修正的NC方法主要是对计算过程噪声的系数进行调整,因此,几乎不影响计算量。估计修正的EM方法和RC方法在标准卡尔曼滤波之外,还要增加状态和协方差修正环节。状态修正式(23)的运算量为:
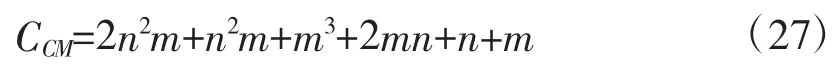
协方差修正式(24)的运算量为:
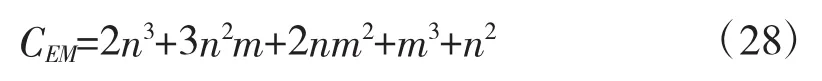
因此,估计修正的运算量为:

取典型值n=4,m=2则CEM=710,CEKF=320。
实际工程中可以对卡尔曼滤波采取一些措施降低运算量:考虑到其中的一些矩阵为对称矩阵,可以采用半角阵进行存储和运算;其中的一些矩阵(如D阵)中含有较多的0元素,优化与零元素有关的运算;对运算量大的代码段进行优化设计。采取这些优化措施后,在Intel Core(TM)i5-2400的3.1 GHz平台上进行测试,进行5,000,000次滤波循环比较的结果如表3所示:
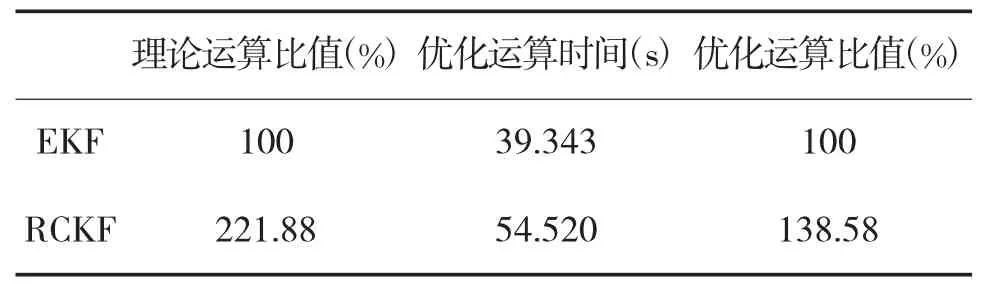
表3 计算量对比
在采用运算优化措施后,RCKF的运算时间比EKF多出38.58%。考虑到如此显著的性能提升,付出一些计算代价在大多数情况下是可以接受的。
4 结论
本文提出了一种道路约束条件下的地面运动目标的跟踪算法。对道路采用路段模型进行描述,构建了路段方程,提出了道路分配算法;根据目标在道路上运动的约束特点,从过程噪声,状态与协方差估计修正,路段切换修正等方面进行了分析与研究,并给出了相应的滤波算法。蒙特卡洛仿真结果表明,融合了道路信息的地面目标机动不确定性大大降低,跟踪性能得到了巨大的提升,证实了道路约束对地面运动目标跟踪的重要意义。各种道路约束方法对性能都有不同程度的改善,其中估计修正方法是性能提升最为明显。本文主要应用于地面单目标跟踪,下一步的研究方向为复杂道路网条件下的地面多目标跟踪。
[1]Chong C Y,Garren D,Grayson T P.Ground Target Tracking-a Historical Perspective [C]//IEEE Aerospace Conference Proceedings,1998.
[2]Blackman S.Integration of a Road Network into a Radar Ground Moving Target Tracking(GMTT)System and Its Performance Evaluation[C]//Signal and Data Processing of Small Targets,2009.
[3]Mallick M,Scala L.IMM Estimator for Ground Target Tracking with Variable Measurement Sampling Intervals[C]//International Conference on Information Fusion,2006.
[4]Simon D,Chia T L.Kalman Filtering with State Equality Constrains[J].IEEE Trans on Aerospace and Electronic Systems,2002,36(1):26-46.
[5]Tahk M,Speyer J L.Target Tracking Problems Subject to KinematicConstraints[J].IEEE Trans on Automatic Control,1990,35(3):324-326.
[6]Herrero J G,Portas J B,Corredera J R.Using of Map Information for Tracking Targets on Airport Surface[J].IEEE Trans on Aerospace and Electronic Systems,2003,39(2):675-692.
[7]Kirubarajan T,Bar-Shalom Y,Pattipati K R.Ground Target Tracking with Variable Structure IMM Estimator[J].IEEE Trans on Aerospace and Electronic Systems,2000,36(1): 26-46.
[8]王建国,何佩琨,龙腾.道路约束在卡尔曼滤波中的应用[J].信号处理,2003,19(4):295-299.
[9]Reid D B.An Algorithm of Tracking Multiple Targets[J]. IEEE Trans on Automatic Control,1979,24(6):843-854.
[10]Li X R,Bar-ShalomY.Multiple-model Estimation with Variable Structure[J].IEEE Trans on Automatic Control,1996,41(4):478-493.
[11]Blackman S,Popoli R.Design and Analysis of Mordern Tracking Systems[M].Norwood,MA:Artech House,1999.
[12]周宏仁,敬忠良,王培德.机动目标跟踪[M].北京:国防工业出版社,1991.
[13]Cormem T H,Leisern C E,Rivest R L.Introduction to Algorithms[M].New York:The Mit Press,2005.
Ground Moving Target Tracking Road Constraint
HE Feng-shou,MIAO Li-feng,ZHANG Ying
(Radar and Avionics Institute,Aviation Lndustry of China,Wuxi 214063,China)
The effective use of road data is probably the most important way that ground target tracking performance can be improved.This paper presents a road constraint algorithm based on Kalmanfilter theory for ground moving target tracking.Road segment model and road segment assignment algorithm are described.An process noise analysis is given about road constrain.Adapted algorithm to the adjacent road is introduced when the state passes a junction.According to the corresponding road parameters,target constrained estimation is modified under Maximum A Posteriori(MAP)solution.The simulation results show that the proposed algorithm is very effective.Quantitative analysis shows that time complexity of the algorithm is acceptable.
ground moving target,tracking,road constraint,Kalman filter
TP391
A
1002-0640(2015)03-0046-05
2014-01-15
2014-03-27
国家“八六三”基金资助项目(2013AA7042013)
贺丰收(1979- ),男,湖南常德人,高级工程师,硕士。研究方向:目标跟踪与数据融合。
