基于量化噪声谱分析的ADC 无杂散动态范围

康荣宗，田鹏武，于宏毅

(信息工程大学 信息工程学院，郑州450002)

0 引 言

无杂散动态范围(SFDR)是衡量ADC 动态范围性能的重要指标。其定义是:当一个正弦信号输入到ADC 时，正弦信号的功率除以在ADC 输出端信号频谱的最大寄生信号峰值功率［1］。这个指标是评价一个ADC 在非常大的信号存在的情况下，能够检测到非常小的信号的能力。在宽带接收设备中，ADC 的SFDR 是制约整个接收系统动态范围的关键因素，因此对于ADC 的无杂散动态范围性能参数的测试和研究很重要。

目前，针对ADC 动态范围的分析方法中，大部分研究者主要针对实际的工程应用测试需求，采用满幅度的正弦信号作为ADC 的输入激励源，对ADC 输出的数据进行统计处理，包括直方图统计［1］、正弦波匹配［2］、傅里叶分析［3］等，但这些方法在具体的测试分析过程中由于受到采样样本数需求过大、测量参数较为单一、频谱泄漏和频谱混叠等因素的影响［4］，并不能得到精确的结果，具有一定的局限性。另有一部分研究者从ADC 的量化误差角度出发，假定量化误差是在量化台阶内均匀分布且与输入信号无关的随机变量，进一步得到ADC 的无杂散动态范围为［5］:

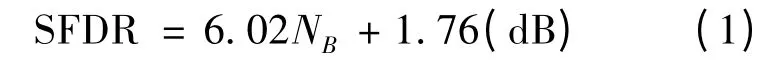
式中:NB是有效量化比特数。

文献［6］将Dither 噪声与输入信号相加后进行ADC 量化，减弱输入信号与量化噪声的相关性，在一定程度上改善了ADC 的SFDR 性能，但受Dither 幅度的影响。此外，将量化误差近似为均匀分布的假设是有一定条件的，如文献［7］建立的量化理论认为如果输入信号的两维特征函数是带限的，那么量化噪声就是与输入无关的白噪声，这一条件是充分而非必要条件;文献［8］进一步建立了充分必要条件，认为如果输入信号的特征函数是一个δ 函数，那么量化噪声谱就是白噪声谱。此外，一些研究者认为输出信号的频谱由离散谐波分量组成，而非白噪声，对量化噪声谱的分布和动态性能进行了确定性分析［9－10］。文献［11］分析了量化后的正弦信号的噪底，推导给出了三次谐波和信噪比的表达式，但并没有对ADC的SFDR 进行分析。文献［12］仅从仿真的角度给出了SFDR 的近似拟合表达式(9N－6)。文献［13］假设输入正弦信号为确定性信号，分析了均匀量化器的SFDR 性能，但假定采样过程和量化过程相互正交，并未考虑采样因素对于其SFDR性能的影响。

本文从ADC 的量化和采样角度出发，首先基于ADC 量化噪声谱的分析，通过数学推导分别给出了在无噪和加性高斯白噪声条件下，单音正弦信号激励的ADC 的SFDR 性能理论上界;阐明了SFDR 与输入信号的幅度、信噪比以及量化间隔等因素之间的关系;进一步推导分析了多音正弦输入下ADC 的量化噪声谱及其对SFDR 性能的影响。最后，结合傅里叶分析法，分析了不同采样率条件下量化噪声谱的分布及其对SFDR 性能的影响。

1 无噪正弦信号输入的SFDR 性能

理想ADC 主要包括采样和量化两个过程，且在一般的情况下采样过程在量化过程之前，为了分析问题的方便，将这两个过程调换了顺序，但并不影响分析的结果［11］。假定输入信号序列xn具有无限的精度，且采用的量化器是均匀量化器，e(x)代表量化噪声。在不考虑溢出的情况下，量化噪声是一个周期的锯齿波，其幅度范围是［－Δ/2，Δ/2］，量化间隔Δ=V/2B－1，V 为ADC 的量程，B 是量化比特数，则e(x)的复指数傅立叶级数为:

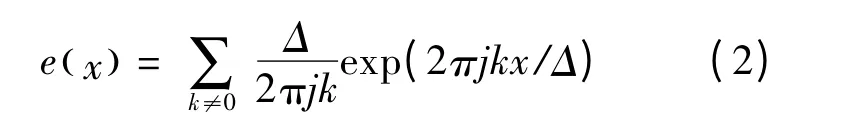
假设量化器的输入信号为:

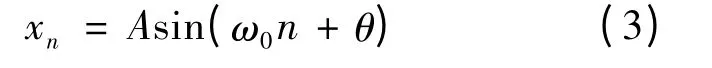
同时假设采样速率是输入正弦信号频率的整数倍。式(3)中:A 为正弦信号的幅度，θ 为均匀分布在［0，2π］的随机变量，那么可以得到:

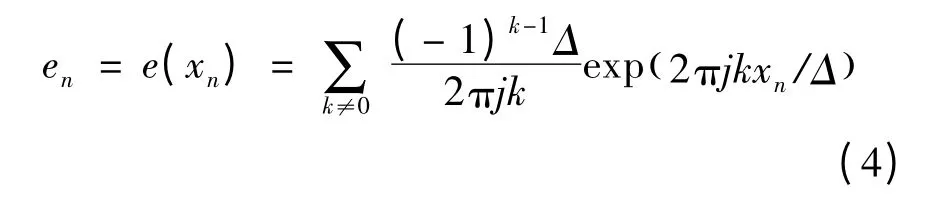
将式(1)代入式(2)，并利用如下Jacobi－Anger 公式:

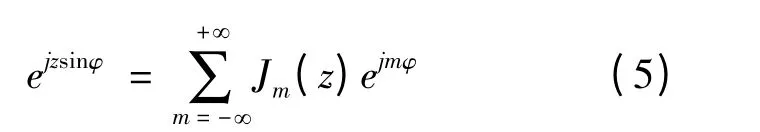
式中:Jm(z)为第一类m 阶贝塞尔函数，则en的均值:

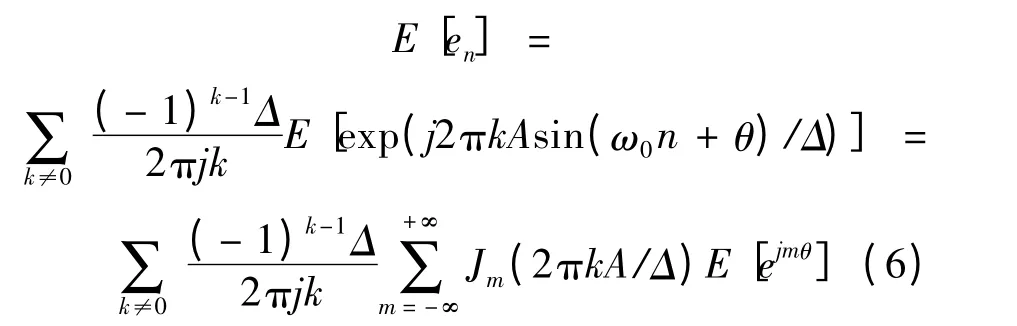
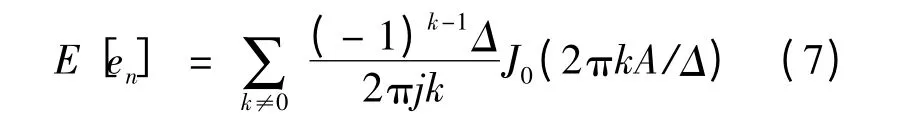
又因为J0(r)=J0(－r)，因此E［en］=0。

利用上述推导方法可以进一步得到en的二阶矩和自相关函数如下:

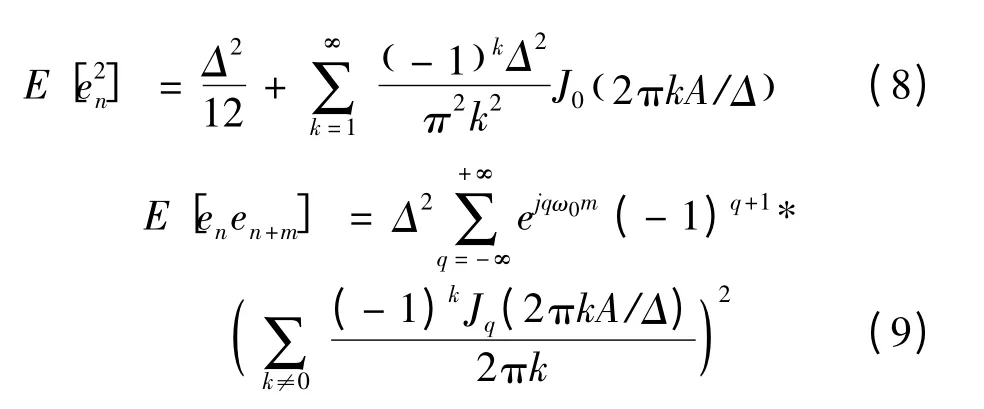
由于J－n(z)=(－1)nJn(z)，上式中，q 为偶数的项就消失了。

由上述推导可以看出，正弦信号输入时的量化噪声是一个平稳随机过程，当量化比特数增大时，V/Δ 增大，而此时J0(2πkA/Δ)→0，en的方差趋于Δ2/12。根据功率谱与自相关函数之间的傅立叶变换关系，就可以得到量化噪声功率谱为:

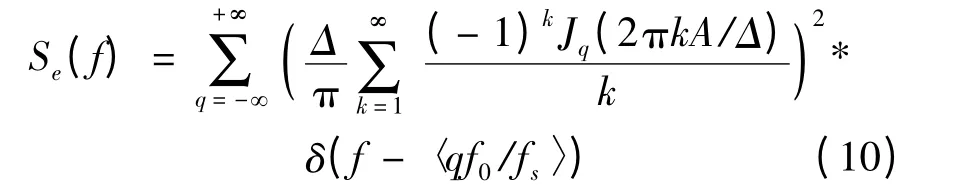
式中:〈qf0/fs〉是qf0/fs的余数;f0=ω0/(2π);q为奇数;fs为采样速率;f 是关于采样速率的归一化频率。

基于ADC 量化过程的基本模型，可以得到量化输出为:

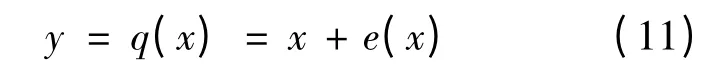
而输出的功率谱为:

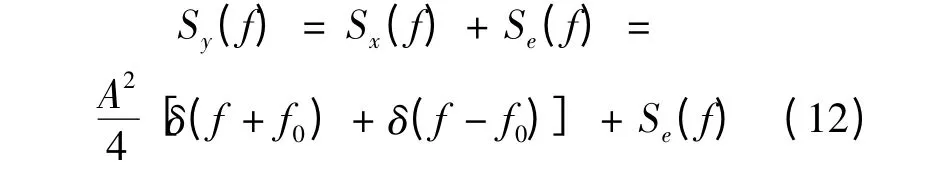
将式(10)代入到式(12)，可以得到:

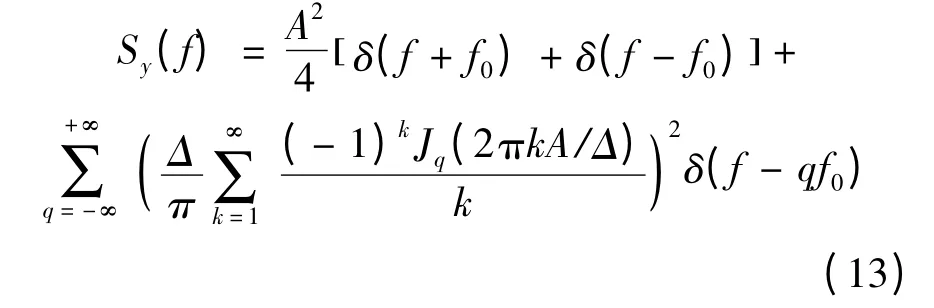
通过上面的分析可知，量化后的正弦信号的功率谱由一系列离散分量组成，而根据双边谱和单边谱的关系，可得到基波分量的输出幅度为:

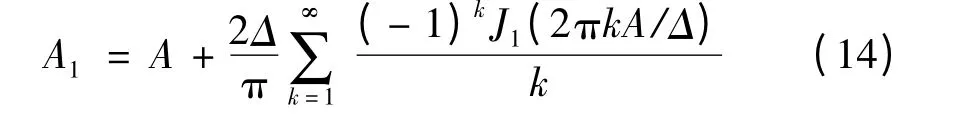
而第p 个谐波分量的幅度Ap为:

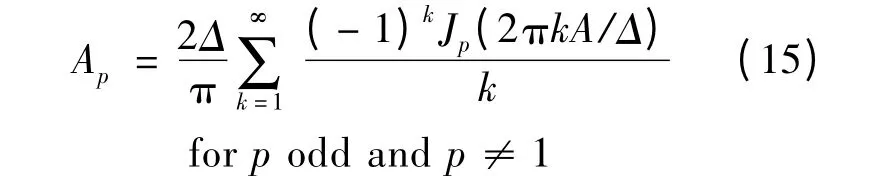
该结果与文献［14］一致，只是推导过程和结论表达形式不同。

通过对式(14)(15)的计算和比较分析，可以获得ADC 量化输出的最大谐波分量Ap*，其频率位置为p*f0，那么ADC 的SFDR 可以定义为量化噪声谱的功率最大的分量与基频分量的比值:

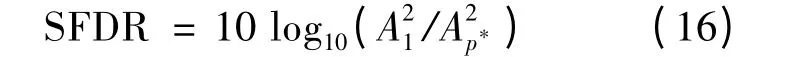
进一步利用Matlab 对式(16)进行仿真分析，图1 给出了不同量化比特位数条件下的最大谐波分量位置。由于Jn(x)在x 非常大时趋于零，且因为量化器的输出包含有限不连续点，因此可以用有限项求和来代替式(14)(15)中无限项求和。这里假定求和项数k=1000，其中量化比特N=log2(A/Δ)+1，而量化间隔Δ=1，从图1 可以看出当量化比特小于3 时，最大谐波分量为三次谐波，而当量化比特位数增大时，谐波分量的位置发生了变化，最大分量分布在2πA 附近［13］。

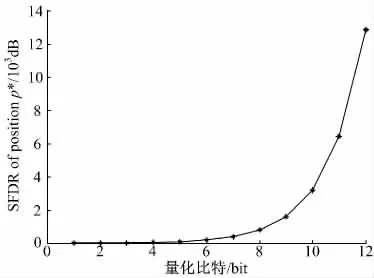
图1 不同量化比特最大谐波分量的位置Fig.1 Location of largest harmonic component of different quantization bits

图2 给出了通过式(16)并结合式(14)(15)和傅里叶分析法［13］得到的不同量化比特下ADC的SFDR 性能，可以看出理论值与仿真结果完全一致，其中式(14)(15)的求和项数k=1000，傅里叶分析法的仿真参数为:采样频率fs=128×64 Hz，FFT 点数为128×64 点，输入信号频率f0=(5×64－1)Hz。

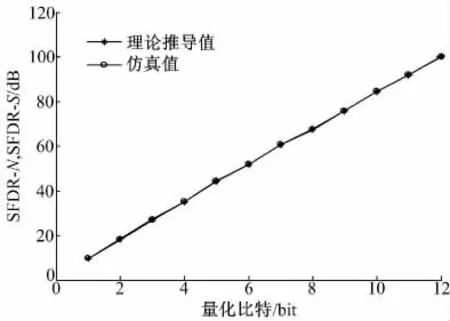
图2 ADC 的SFDR 性能的理论值和仿真值Fig.2 Theoretical and simulated value of SFDR performance of ADC

由此，在一定量化误差范围内，进一步利用最小二乘拟合可以得到理想ADC 的SFDR 性能和量化比特N 之间的表达式为:

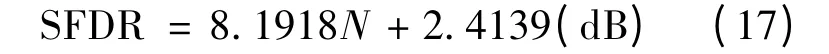
2 AWGN 下正弦信号的SFDR 性能

下面分析加性高斯噪声对于量化噪声谱的影响，即假定输入信号为:

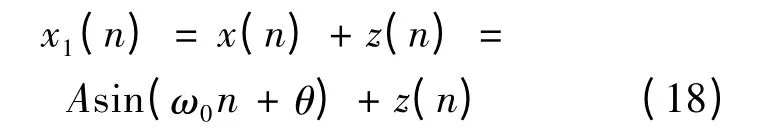
式中:z(n)为均值为0、方差为σ2的高斯白噪声，类似于上一节的分析方法，根据高斯变量的特征函数性质，可知E{exp(jαz)}=exp(－α2σ2/2)，则可以得到:

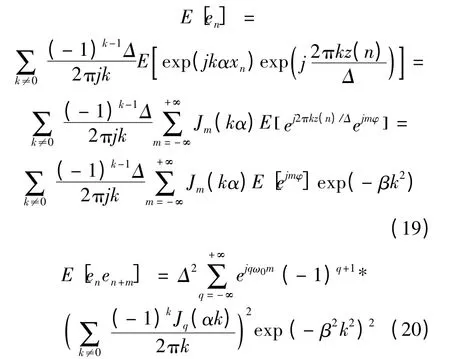
式中:α=2πA/Δ;β=2π2σ2/Δ2。

根据功率谱与自相关函数之间的傅立叶变换关系，就可以得到量化噪声功率谱为:

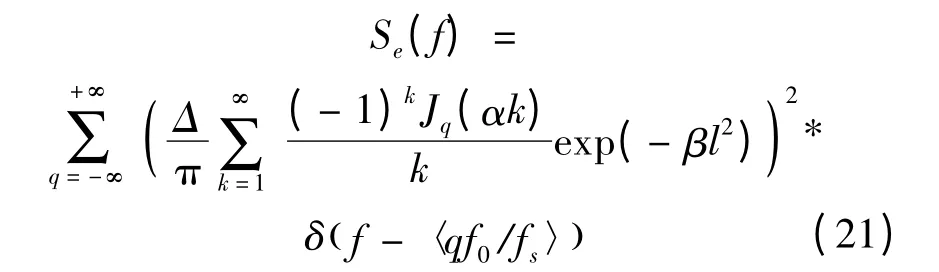
因此，加性高斯噪声条件下ADC 输出的基频分量的幅值为:

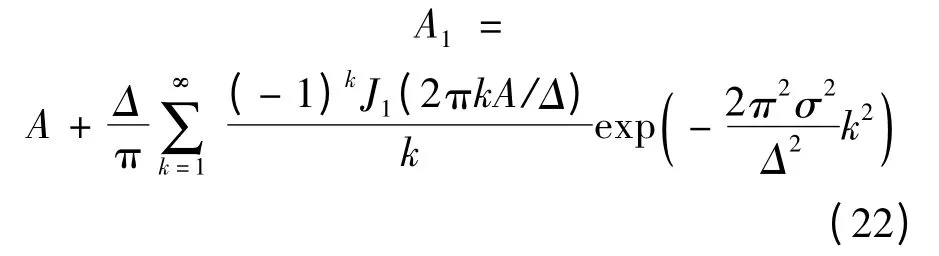
而第p 个谐波分量的幅值为:

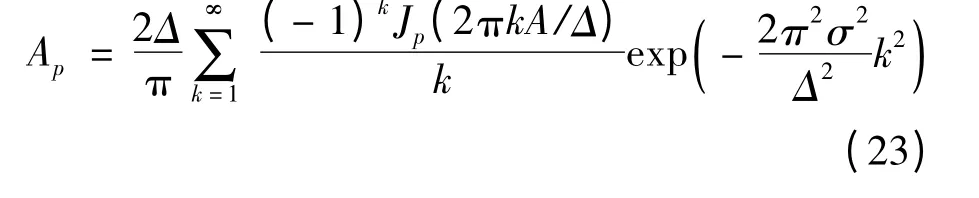
将式(22)(23)代入式(16)，可以得到高斯信噪比下的ADC 的SFDR 的具体表达式。图3 给出了ADC 的SFDR 性能和(σ/Δ)2之间的关系。

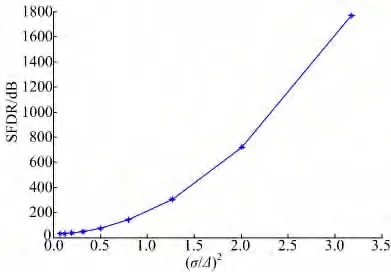
图3 ADC 的SFDR 性能和(σ/Δ)2 的关系Fig.3 Relationship between SFDR of ADC and(σ/Δ)2

结合上面的分析可知，谐波分量的幅值及其ADC 的SFDR 性能依赖于σ/Δ，当这个比值大于1 时，谐波分量的幅值被明显削弱甚至消失，ADC的SFDR 性能随着高斯噪声的增大而明显增大。这是由于在高斯白噪声条件下，噪声本身具有的随机性破坏了量化噪声的规律，因此在ADC 的性能评估中必须充分考虑输入噪声的影响。

3 多音正弦信号输入的SFDR 性能

下面分析多音正弦输入情况下，ADC 的量化噪声谱的分布情况。首先考虑当输入为两个正弦信号的情况，假设输入信号为:

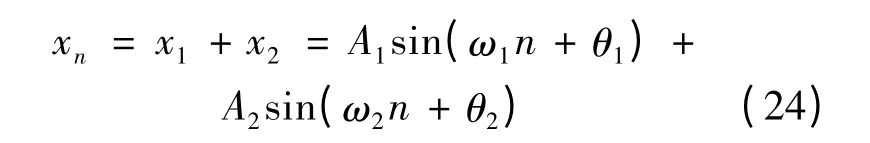
式中:A1和A2分别为两个正弦信号的幅度;θ1和θ2为均匀分布在［0，2π］的随机变量。

同样利用上述推导方法，可以得到量化噪声的功率谱为:

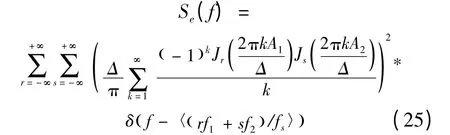
式中:r 和s 是奇偶性相反的整数。当输入为N个正弦信号时的量化噪声谱为:

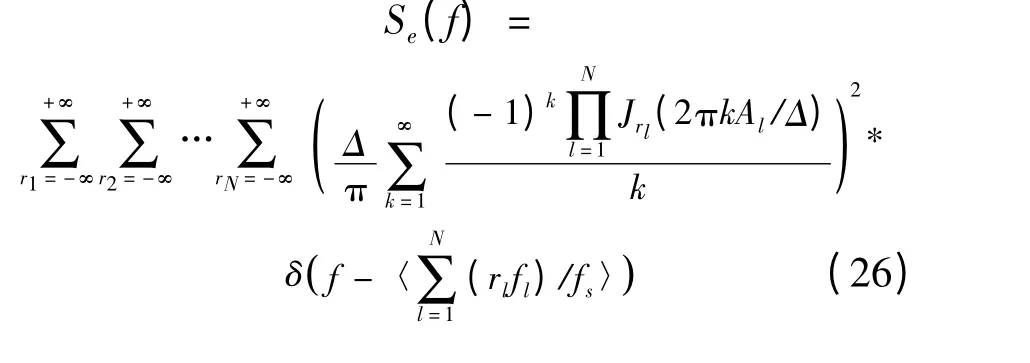
4 采样率对SFDR 的影响

根据ADC 的一般分析模型，采样是量化之后必不可少的一个环节，而采样后的信号以采样频率为周期在频谱上无限拓展。通过上面的分析，可知激励信号经过ADC 的量化之后，特别是在量化比特大于3 时，其最大谐波分量的位置位于奈奎斯特区间之外，采样率fs往往无法满足其Nyquist 采样的要求而导致谐波分量的镜像混叠，从而破坏原来谐波分量之间的关系，使得ADC 输出的谱分布产生非线性变化，而这种变化趋势主要依赖于采样频率fs和输入信号频率f0的关系。下面结合Matlab 仿真重点分析在三种不同fs和f0的关系下，输出离散谱的分布及其对SFDR 性能的影响。

Case1 fs和f0互为质数

当采样频率值和输入信号频率值互为质数时，在不同的信号周期里，信号的采样值将具有不同的相位值，其采样值接近于随机的位置不具有周期性。量化噪声谱中大于fs/2 的谐波频率在向［0，fs/2)内折叠时，并不会与其他的低阶谐波分量产生碰撞，如图4 所示，其中f0=319 Hz，fs=128×64 Hz，量化比特N=4;ADC 的SFDR 性能如图5 所示，可以看出SFDR 值并不随着采样率的变化而变化，此时有利于ADC 实际动态性能的测试。

Case2 fs为f0的整数倍

当采样频率为输入信号频率的整数倍时，根据一般的镜像混叠机理可以得到高阶谐波分量的混叠频率位置计算公式。假定量化之后的高阶谐波分量的频率为fp，采样频率为fs，其中fs＜2fp，采样得到的混叠后的频率为fp^，则有:

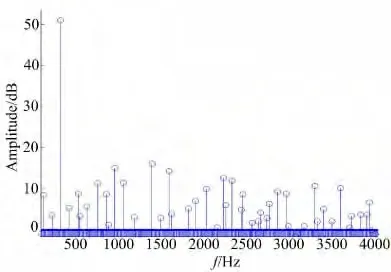
图4 fs 和f0 互为质数的ADC 的离散谱Fig.4 Discrete spectrum of ADC when fs and f0 are relative primes

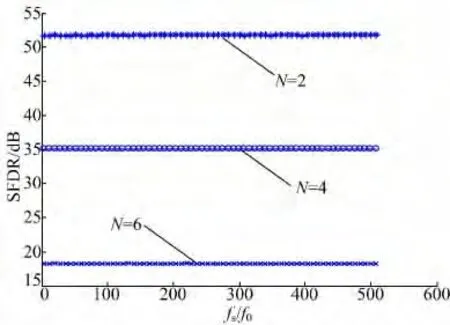
图5 fs 和f0 互为质数的SFDR 性能Fig.5 SFDR performance of ADC when fs and f0 are relative primes

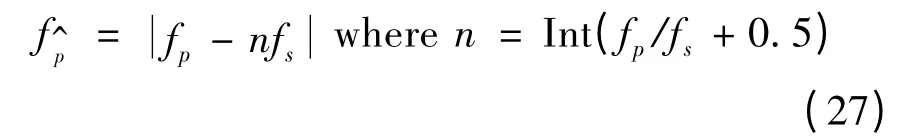
式中:Int 表示将小数点后面的数字全部丢弃，仅保留小数点之前的整数部分。

定义R 为fs被fp整除的余数，那么式(27)表示当R 小于fs/2 时，fp^ =R，否则fp^ =fs－R。

图6 给出了当fs/f0为整数时，正弦信号经过ADC 的量化和采样过程之后的谱分布，其中f0=512 Hz，fs=64×512 Hz，量化比特N=3。从图6可以看出，ADC 输出的离散谱位置将出现非线性变化，特别是当fs/f0为奇数时，其主要能量将不再仅分布在基频和其奇数倍谐波分量的位置上，在偶数倍基频的位置上也可能出现较大的谐波分量。

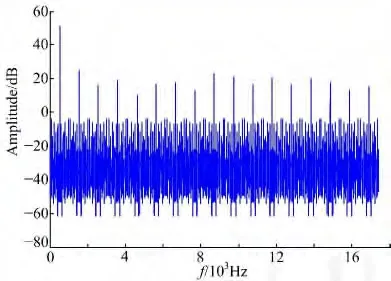
图6 fs/f0 为整数的ADC 输出离散谱Fig.6 Discrete spectrum of ADC when f0 divides fs

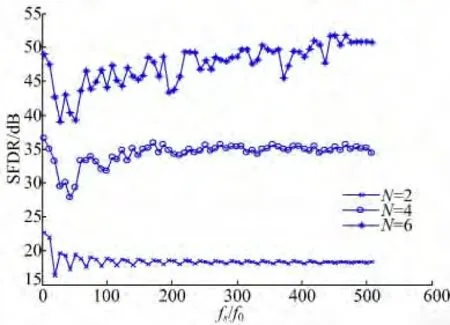
图7 不同整数倍fs/f0 的SFDR 性能Fig.7 SFDR performance of ADC when f0 divides fs

图7 给出了在不同量化比特N=2、4、6 的条件下，不同采样频率的SFDR 的分布情况。从图7可以看出由于欠采样引起的频谱镜像混叠作用，ADC 的SFDR 不再是一个恒定值。在采样率相对较低时，在奈奎斯特频率范围内，其镜像混叠作用明显，SFDR 性能由于具体的采样倍数和谐波分量分布的影响而呈曲线变化趋势。随着采样率的不断提高，量化噪声功率分布到更宽的频谱范围之内，镜像混叠的作用相对减弱，最后收敛于未考虑采样的情况。此外，量化位数越小，其各谐波分量的幅值越大，但由于总的噪声能量不变，使得谐波分量与基频分量的幅值相对差值越小，则ADC的SFDR 性能的收敛速度越快。

Case3 fs和f0具有大于1 的最大公约数

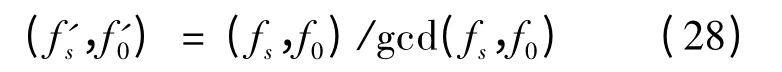
式中:gcd 表示最大公约数。

图8 给出了该条件下的正弦信号输入的ADC 的输出离散谱分布，其中f0=5×64 Hz，fs=128×64 Hz，gcd(fs，f0)=64，量化比特N=4。ADC量化采样后的信号重复周期为f's=128，每个重复周期内包含了f'0=5 个正弦信号周期，则量化误差的谐波中包含了一个以gcd(fs，f0)为基频的分量，主要分布在3*gcd(fs，f0)，5*gcd(fs，f0)，…，(2n+1)*gcd(fs，f0)的位置上，其中n 为整数，由于假定采样速率和FFT 点数为2 的整数倍，输入信号的频率f0=f'0*gcd(fs，f0)，则f'0为奇数，也即输入信号的频率必定与谐波分量重叠。

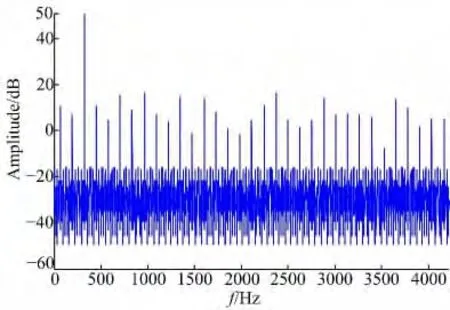
图8 fs 和f0 具有公约数的ADC 输出信号谱Fig.8 Discrete spectrum of ADC when fs and f0 have a common divisor

图9 给出了fs和f0具有最大公约数条件下ADC 的SFDR 性能随着信号频率变化的趋势。从图9 可以看出，由于输入信号的频率位置和谐波分量相互重叠，使得其基频位置的谐波幅值增大，而相对于Case2，其谐波分量分布的频率范围更广，镜像混叠的作用相对减弱，因此其SFDR 性能的收敛速度更快。

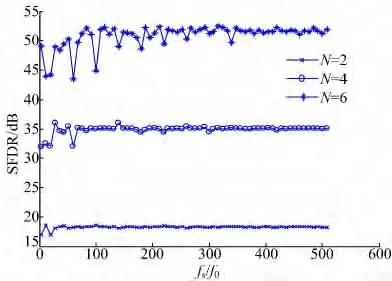
图9 fs 和f0 具有最大公约数的SFDR 性能Fig.9 SFDR performance of ADC when fs and f0 have a common divisor

5 结束语

在ADC 量化噪声谱分析的基础上，首先从理论上推导给出了ADC 的SFDR 性能的数学表达式，并给出了理想条件下SFDR 的最小二乘拟合上界，进一步分析了输入信号幅度、量化台阶、加性高斯白噪声、多音正弦输入等因素对其性能的影响，为实际ADC 性能的测试和系统的设计提供了理论依据。接着分析了采样因素对ADC 的SFDR 性能的影响，结合Matlab 仿真重点分析了采样率和输入信号频率在互为质数、具有最大公约数、整数倍等不同条件下的ADC 输出离散谱和SFDR 性能的变化趋势。从仿真结果及其分析可以看出，在两个频率值互为质数时，其SFDR 性能稳定，最有利于对ADC 的SFDR 性能进行测试，而具有最大公约数下的性能好于整数倍的情况，此外，采样频率越大其性能越趋近于稳定值。当然，采样频率、量化精度、输入信号幅度等因素在实际测试和应用中也受到具体器件性能和测试信号的制约，在具体工程设计中需要综合考虑。

［1］Wagdy M F，Awad S S.Determining ADC effective number of bits via histogram testing［J］.IEEE Trans Instrumentation Measurement，1991，40(4):770－772.

［2］Kollar I.Improved determination of the best fitting sine wave in ADC testing［J］.IEEE Trans Meas，2005，54(5):1978－1984.

［3］Benetazzo L，Narduzzi C.A/D converter performance analysis by a frequency－domain approach［J］.IEEE Trans Instru Meas，1992，41(6):834－840.

［4］JAMES T.宽带数字接收机［M］.2 版.杨小牛译.北京:电子工业出版社，2002.

［5］Kester W.Understand SINAD，ENOB，SNR，THD，THD+N，and SFDR so you don＇t get lost in the noise floor［J］.Analog Devices Tutorial，2009，10(8):1－8.

［6］郭志勇，李广军，李强.用于提高ADC 性能的自适应Dither 结构［J］.电子科技大学学报，2011，40(3):375－378.Guo Zhi－yong，Li Guang－jun，Li Qiang.Self－adapting dither structure for improving ADC performance［J］.Journal of University of Electronic Science and Technology of China，2011，40(3):375－378.

［7］Widrow Bernard，Kollar Istvan，Liu Ming－Chang.Statistical theory of quantization［J］.IEEE Transactions on Instrumentation and Measurement，1996，45(2):353－361.

［8］Spripad Anekal B，Snyder Donald L.A necessary and sufficient condition for quantization errors to be uniform and white［J］.IEEE Transaction on Acoustics，Speech，and Signal Processing，1977，25(5):442－448.

［9］Blachman N.The intermodulation and distortion due to quantization of sinusoids［J］.IEEE Trans on Acoustics，Speech，and Signal Processing，1985，33(6):1417－1426.

［10］Perez－Alcazar P R，Santos A.Behavior of quantization noise for sinusoidal signals［J］.Journal of Applied Research and Technology，2009，7(2):136－152.

［11］Bellan D，Brandolini A，Gandelli A.Quantization theory －a deterministic approach［J］.IEEE Trans on Instrumentation and Measurement，1999，48(1):18－25.

［12］Pan H，Abidi A A.Spectral spurs due to quantization in nyquist ADCs［J］.IEEE Trans on Circuits and Systems，2004，51:1422－1439.

［13］Alink M S O.Spurious－free dynamic range of a uniform quantizer［J］.IEEE Transactions on Circuits and Systems II:Express Briefs，2009，56(6):434－438.

［14］Ghittori N，Vigna A，Malcovati P.Analysis of the ideal SFDR limit for an N bit digital－to－analog converter［C］∥The 12th IEEE International Conference on Electronics，Circuits and Systems，Gammarth，2005:11－14.