连续相位调制信号的载波相位软同步算法

周相超，薛 睿，赵旦峰，付 芳

(哈尔滨工程大学 信息与通信工程学院，哈尔滨150001)

0 引 言

连续相位调制(CPM)是一类先进的调制技术，具有相位连续、频谱特性优良的特点，与PSK调制相比，具有更高效的频带利用率和功率利用率，而且调制之后的信号包络恒定，对功率放大器的非线性特性不敏感，非常适合于信道传输。目前，CPM 的两种特例MSK 和GMSK 已广泛应用于卫星通信、深空通信和以GSM 为代表的数字蜂窝移动通信等领域，但因接收机复杂度较高、信号同步存在较大困难，通用的CPM 尚未获得广泛的应用［1］。

目前，CPM 信号的载波同步方法主要分为数据辅助同步和非数据辅助同步［2］。数据辅助同步方法的同步性能较好，但需占用额外的传输带宽和功率;非数据辅助同步方法不需额外的带宽和功率，但同步精度较差，且仅适用于信噪比较高的情况，很难实现有效同步。

近年来，随着具有接近香农限的高性能的Turbo 码和LDPC 码的广泛应用，逐渐兴起了一类新的“码辅助同步”算法。码辅助同步算法基于最大似然准则，将译码器与同步器进行联合迭代，从而获得接近理想的载波同步性能。文献［3］将Turbo 码译码结构与最大似然准则结合，基于期望最大算法与和积算法进行迭代载波同步，可以获得较精确的同步;文献［4］提出了基于译码软信息的改进的极性判决相位检测算法，在低信噪比条件下可获得较传统方法更理想的同步性能;文献［5］通过将锁相环与LDPC 译码器结合，使用迭代译码过程中的外信息来获得接近理想的相位估计;文献［6］提出一种基于译码软信息反馈的载波同步算法，不需导频序列即可获得载波相位的最佳估计值;文献［7］基于最大似然准则，提出简化的导频联合编码辅助载波同步算法，该算法能大幅提高同步参数的估计精度和范围，在一定的导频长度下可逼近理想同步;文献［8］中针对SCCPM 串行级联系统，提出一种Turbo 同步结构，通过CPM 信号的正交指数分解和卡尔曼滤波来估计载波相位;文献［9］针对LDPC－CPM 迭代系统，提出一种最大化后验概率均值的载波同步算法。

由Rimoldi 分解可知:CPM 信号可以分解为连续相位编码器CPE 和无记忆调制器MM 的组合［10］，因此CPM 信号具有类似于卷积码的网格记忆结构。本文在Rimoldi 分解的基础上，借鉴Turbo 码和LDPC 码的“码辅助同步”思想，提出一种通用的CPM 信号载波相位同步算法。该算法基于最大似然准则，分别使用MAP 算法和EM算法对CPM 信号进行解调和相位估计，将解调器和同步器联合设计，利用解调器输出的软信息辅助载波相位的同步。

1 CPM 调制与系统模型

1.1 CPM 调制原理

CPM 信号具有相位连续、包络恒定的特点，其复指数形式的表达式为［11］:

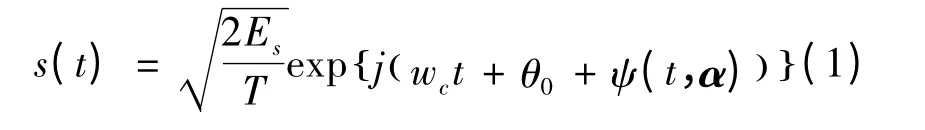
式中:Es是符号能量;T 是符号周期;wc是载波频率;θ0是初始相位;α 是传输的符号信息，取值范围为{±1，±3，…，±(M－1)}，M 为CPM 的进制数;ψ(t，α)是携带信息的相位超量，同时也决定信号的带宽，定义式为:

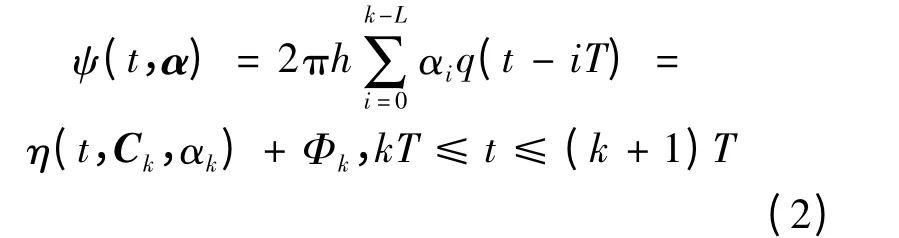
式中:h 为CPM 信号的调制指数;L 为CPM 的记忆长度;η(t，Ck，αk)和Φk分别为相位分支和相位状态，定义式分别为:

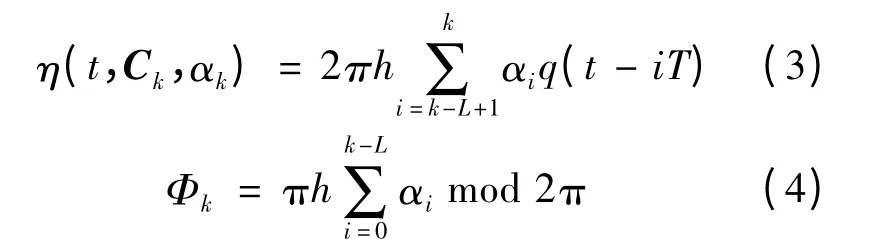
式中:向量Ck=(αk－L+1，…，αk－2，αk－1)是符号信息序列，称为相关状态。

CPM 信号的相位响应函数q(t)的表达式为:

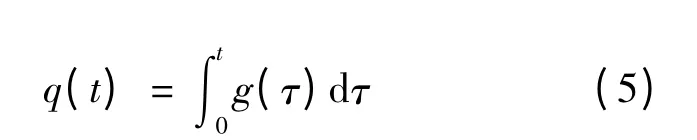
具有以下特性:

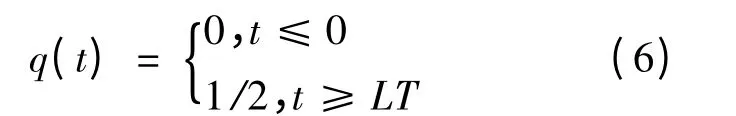
g(t)称为CPM 的频率响应函数，主要有矩形波成型函数、余弦波成型函数和高斯脉冲成型函数，对应不同的CPM 类型。

1.2 CPM 软解调算法

传统的CPM 信号使用Viterbi 算法实现相干解调，不便于软信息的提取，为此，采用MAP 算法对CPM 信号进行软解调，以获取载波相位同步所需的软解调信息。

由Rimoldi 分解可知，CPM 信号隐含一个具有记忆性的网格编码器，类比卷积码的网格图，可定义k 时刻CPM 信号的状态为:σk=(Φk，Ck)，对应的k+1 时刻的状态即为:σk+1=(Φk+1，Ck+1)，相邻时刻两个相位状态之间的关系为:

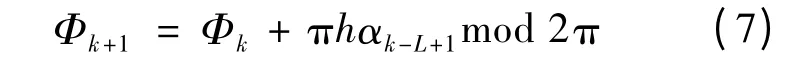
CPM 信号的网格图如图1 所示，其中sS(e)和sE(e)分别表示起始状态和结束状态，u(e)和c(e)分别表示输入信息符号和输出码字符号，S={s1，…，sn}表示状态集合，U={u1，…，um}表示输入符号集合，ξ=S×U={e1，…，emn}表示任意两个网格状态之间的所有可能状态转移。

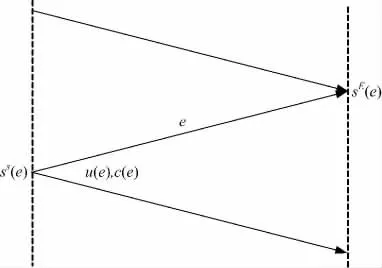
图1 CPM 网格状态图Fig.1 CPM trellis

根据MAP 算法的原理:若网格状态图已知，则输出码字概率、输入比特概率、状态转移概率等多种概率分布均是可计算的，根据码辅助同步思想，在推导CPM 信号的载波相位同步算法的过程中，可由MAP 算法计算所需的解调软信息类型。

1.3 系统模型

本文给出的算法和仿真都是基于图2 的系统模型的。系统采用Rimoldi 分解的方式产生CPM信号，解调为基于MAP 算法的软解调方式，传输信道为高斯白噪声信道(AWGN)，其双边功率谱密度为N0/2。假定系统具有理想信号增益和符号定时同步，码间干扰可忽略。

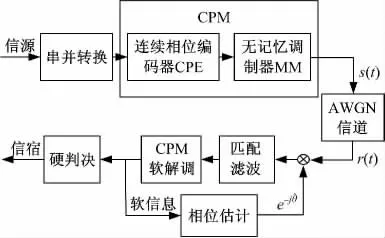
图2 CPM 系统模型Fig.2 CPM system model

CPM 信号s(t)经AWGN 信道传输，到达接收机的信号r(t)表达式为:

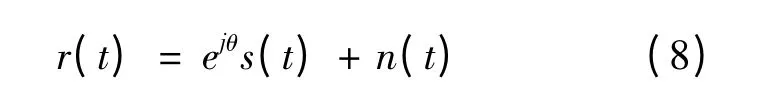
式中:n(t)是经过AWGN 信道引入的零均值复高斯白噪声，其同相分量与正交分量相互独立，方差为N0/2;θ 是未知且恒定或慢变的载波相位，需要对其进行估计和补偿。

2 载波相位软同步算法

2.1 载波相位的最大似然估计

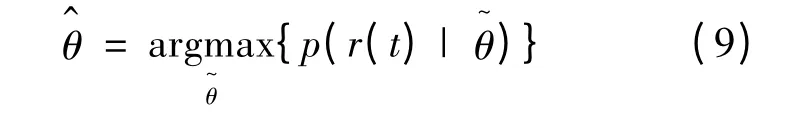
在CPM 信号的最大似然检测中，匹配滤波器用于产生软解调的先验信息，输出度量定义为:

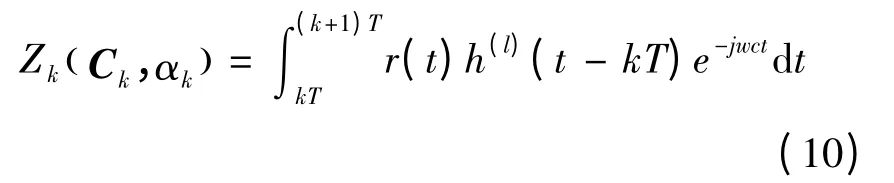
式中:h(l)(t)为匹配滤波器单位冲击响应，表达式为:

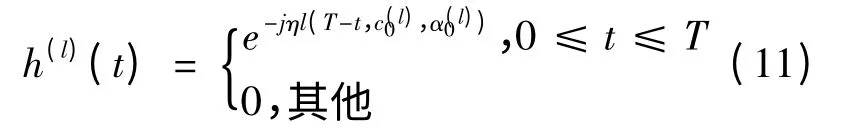
表示网格图中一条可能的传输路径。在CPM 信号的网格图中，从一个节点sS(e)出发，共有M 个分支，每一条分支对应当前的输入符号αk，定义分支度量为:

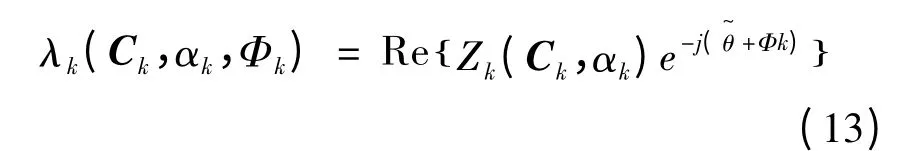
因此，载波相位θ 的似然函数可表示为:

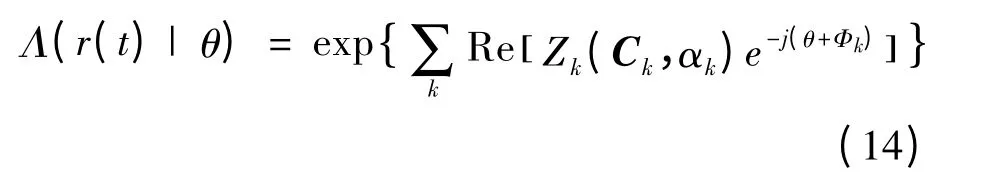
由最大似然准则，为估计载波相位，需要对式(14)求导，令导数为零，得到载波相位的最大似然估计值，但方程没有闭环解，数学求解困难，因此需要使用其他方法来近似，传统方法有数据辅助和非数据辅助的近似方法［13］，本文使用EM 算法，采用迭代方式逐步接近载波相位的最大似然估计。

2.2 EM 算法

EM 算法是一种广泛应用于参数估计领域的迭代求解算法，适用于存在隐含变量的优化问题，算法的目标是找出包含隐性变量的概率模型的最大可能的解［14］。EM 算法包括E 步骤和M 步骤，经过E 步骤和M 步骤的多次迭代，可获得未知参数的近似最大似然估计值。

在E 步骤中构造Q 函数:

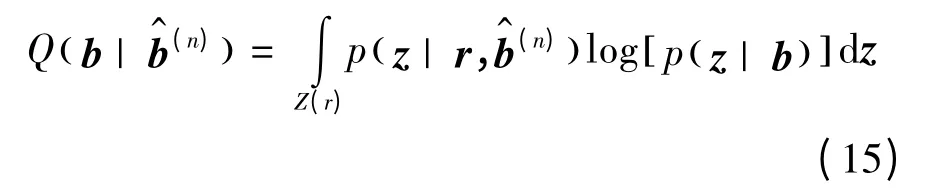
M 步骤用于获取新的估计值:

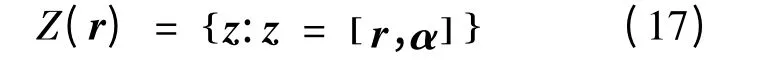
2.3 基于解调软信息的载波相位估计

接收信号的表达式如式(8)所示，载波相位θ为待估计参数，由EM 算法，构造Q 函数:

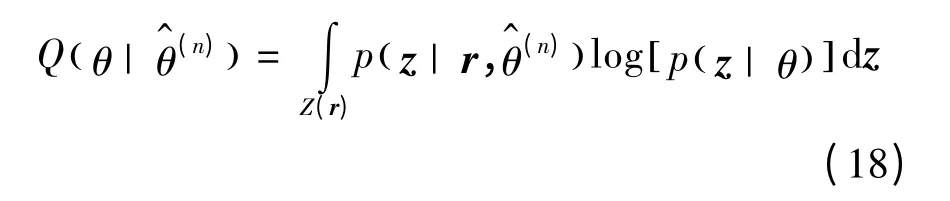
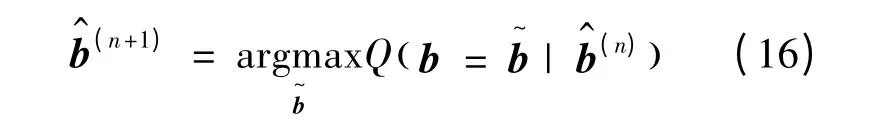
由式(17)可将后验概率p z|( θ) 作如下化简:

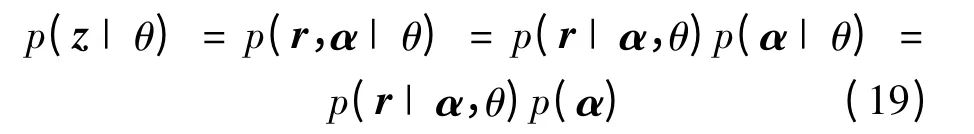
将式(17)和式(19)带入式(18)可得:

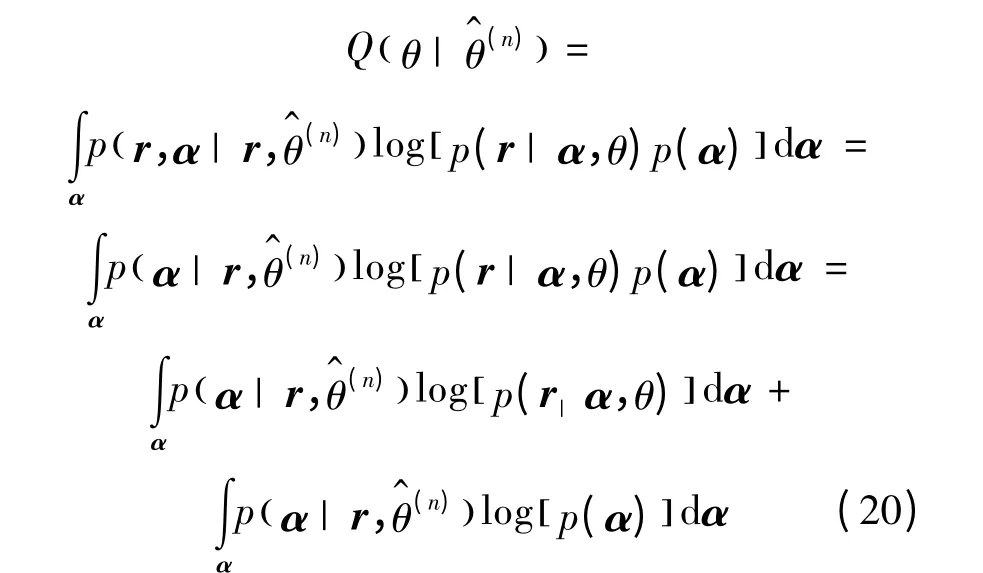
式中:最后一个等号右边第二项与相位θ 无关，可直接忽略，因此，载波相位θ 的Q 函数可简化为:

因传输信道为AWGN 信道，似然函数p(r|α，θ)可表示为:

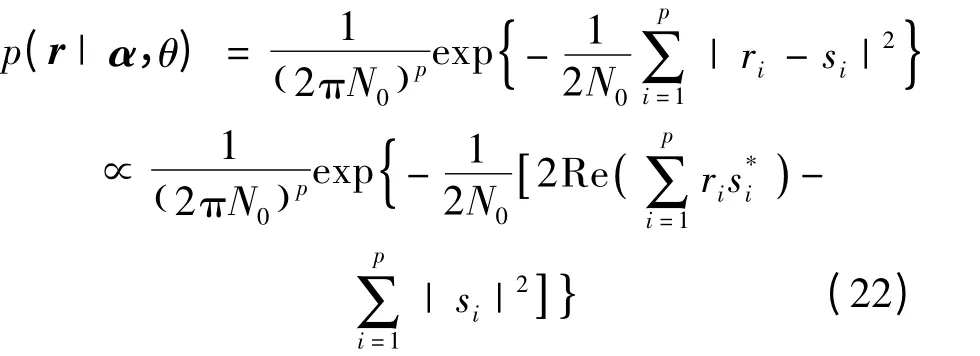
因此Q 函数中的对数似然函数为:

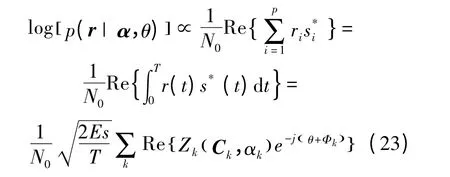
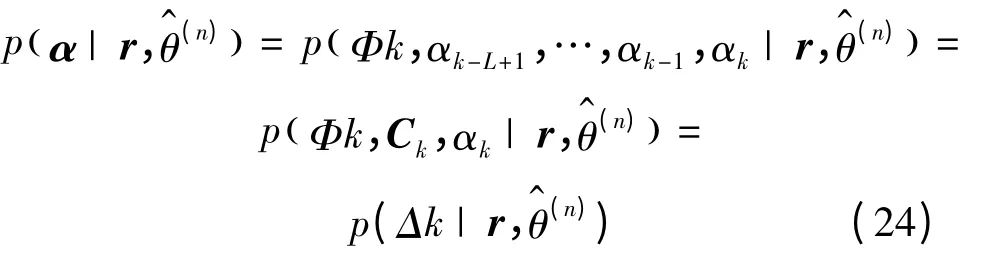
综合式(23)的对数似然函数和式(24)的后验概率表达式，CPM 信号载波相位θ 的Q 函数最终可表示为:

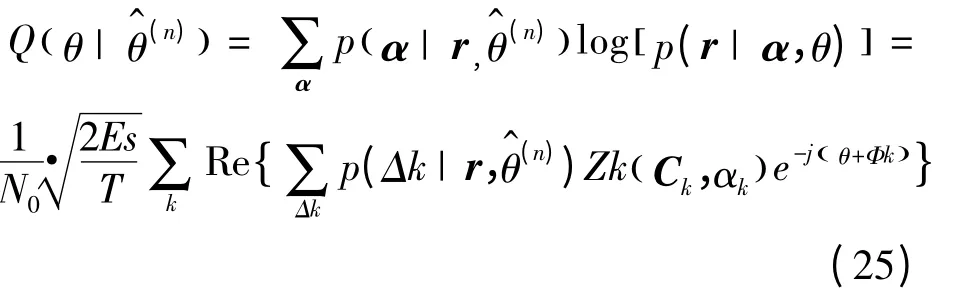
因此，基于EM 算法对CPM 信号的载波相位进行估计时需要2 种信息，Zk(Ck，αk)和p(Δk|，Zk(Ck，αk)来自匹配滤波器的输出度量，状态转移概率可由CPM 信号自身的MAP 软解调算法获得。

由EM 算法原理，在获得Q 函数之后，通过M步骤中的取最大值操作，即可获取载波相位θ 的迭代估计值，由式(25)可得:

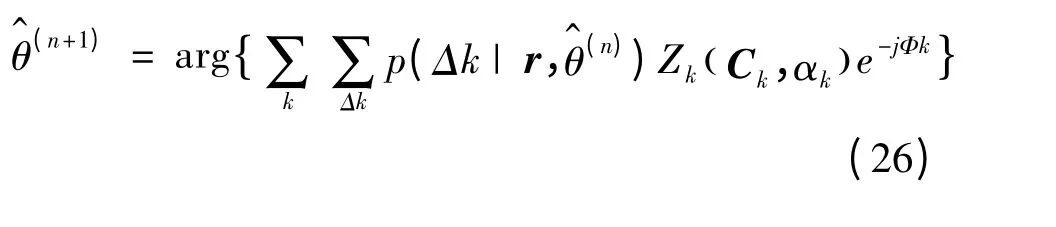
至此，推导出了基于EM 算法和CPM 软解调的载波相位软同步算法，该算法利用解调器输出的状态转移信息来辅助载波相位估计，以迭代的方式获得接近最大似然的载波相位同步，既避免了最大似然估计求解困难的问题，又可获得较高的估计质量。

3 系统仿真与性能分析

基于图2 所示的系统模型对本文提出的CPM 信号的载波相位软同步算法进行性能仿真，仿真参数设置如下。采用的CPM 信号类型为:进制数M=8，记忆长度L=2，调制指数h=1/2，成型函数使用升余弦型;帧长为N=512，进行10 000 帧仿真;载波相位同步器与软解调器之间的最大迭代次数设为10 次;载波相位偏移量的范围设定为－180°≤θ ≤+180°;归一化信噪比的范围设为0≤Eb/N0≤10 dB。为验证本文所提软同步算法的有效性，分别对CPM 信号的载波相位估计精度和误码率性能进行数值仿真。

图3 给出了载波相位估计的均方误差曲线，作为对比，同时给出修正克拉美罗限(MCRB)、传统的数据辅助估计(DA)的均方误差曲线，其中，载波相位的修正克拉美罗限为［15］:

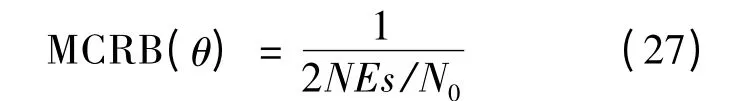
由图3 可以看出，当Eb/N0≥5 dB 时，载波相位软同步算法的均方误差估计性能逐渐接近MCRB，与传统的DA 方法性能相近。

图4 给出了在多种相偏、不同信噪比条件下CPM 信号的误码率性能，由图4 可见，当Eb/N0≥5 dB 时，载波同步逐渐趋于收敛，系统性能损失低于0.1 dB，相位偏差对系统性能的影响得到抵消，系统的误码率接近理想同步系统的性能。

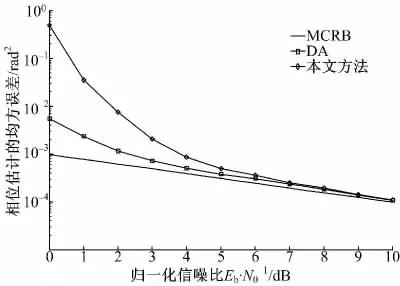
图3 载波相位估计的均方误差曲线Fig.3 RMSEE curves of phase estimation

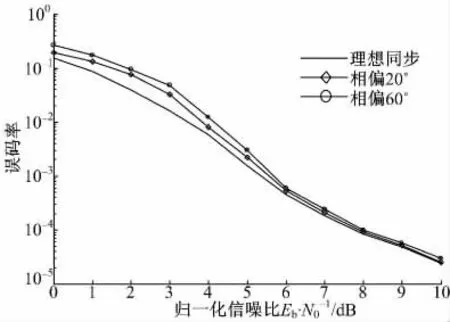
图4 不同相位偏移时CPM 信号的误码率性能曲线Fig.4 BER curves of CPM for different phases

图5 给出了CPM 信号在归一化信噪比为6 dB 和8 dB 条件下相位估计的范围。可以看到:相位未补偿时，误码率受相位偏移影响较大，使用本文算法对载波相位偏移补偿之后，误码率性能得到改善;该算法能有效估计的相位偏移范围是|θ|＜90°，在该范围内，估计误差足够小，误码率性能接近理想同步情况。

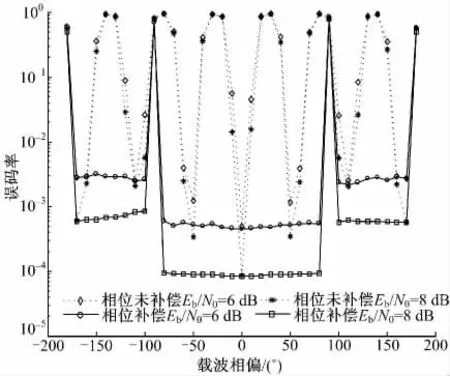
图5 CPM 信号的相位补偿曲线Fig.5 Phase compensation curves for CPM

4 结束语

因同步困难，CPM 信号的应用受到较大局限，本文借鉴最新的码辅助同步思想，基于最大似然准则，将CPM 信号的解调器与同步器联合，利用解调器输出的软信息去辅助载波相位的估计，从而达到载波相位同步的目的。当Eb/N0≥5 dB时，相位估计误差接近MCRB，系统的误码率性能损失低于0.1 dB，可估计的相位偏移范围为| θ|＜90°，经相位补偿，系统的误码率接近理想同步条件下的性能。本文算法适用于载波相位恒定或慢变的系统，以少量的系统复杂度为代价，达到近似理想载波相位同步的目的，具有良好的工程实用价值。

［1］Mengali U，Andrea A.Synchronization Techniques for Digital Receivers［M］.New York:Plenum，1997.

［2］Bianchi P，Loubaton P，Sirven F.Non data－aided estimation of the modulation index of continuous phase modulations［J］.IEEE Trans on Signal Processing，2004，52(10):2847－2861.

［3］Herzet C，Noels N，Lottici V，et al.Code－aided turbo synchronization［J］.Proceedings of the IEEE，2007，95(6):1255－1271.

［4］张忠培，高中杰，徐俊辉.高阶调制码辅助同步算法研究［J］.电子科技大学学报，2011，40(6):825－828.Zhang Zhong－pei，Gao Zhong－jie，Xu Jun－hui.Code－aided synchronization algorithm for high－order QAM［J］.Journal of University of Electronic Science and Technology of China，2011，40(6):825－828.

［5］刘荣科，李满庆，侯毅.基于提前停止判决的编码软信息辅助载波同步［J］.航空学报，2012，33(4):715－721.Liu Rong－ke，Li Man－qing，Hou Yi.Code－aided carrier synchronization via soft decision feedback based on early stopping criterion［J］.Acta Aeronautica et Astronautica Sinica，2012，33(4):715－721.

［6］Valles E L，Wesel R D，Villasenor J D，et al.Pilotless carrier phase－synchronization via LDPC code feedback［C］∥IEEE Military Communications Conference，San Jose，2010:2068－2073.

［7］史治平，唐发建，晏辉，等.极低信噪比下的导频联合编码辅助载波同步算法［J］.电子与信息学报，2011，33(10):2506－2510.Shi Zhi－ping，Tang Fa－jian，Yan Hui，et al.Joint assisted carrier synchronization algorithm by pilot and code at extremely low SNR［J］.Journal of Electronics and Information Technology，2011，33(10):2506－2510.

［8］Qing Zhao，Stuber G L.Turbo synchronization for serially concatenated CPM［C］∥IEEE International Conference Communication，2006:2976－2980.

［9］Zhao D F，Zhu T L，Zhang Y Q.Code－aided synchronization algorithm based on posterior probability［C］∥The 3rd International Conference on Communication Software and Networks，Xi＇an，IEEE，2011:607－611.

［10］Rimoldi B E.A decomposition approach to CPM［J］.IEEE Transactions on Information Theory，1988，34(2):260－270.

［11］Noels N，Moeneclaey M，Simoens F，et al.A lowcomplexity iterative phase noise tracker for bit－interleaved coded CPM signals in AWGN［J］.IEEE Transactions on Signal Processing，2011，59(9):4271－4285.

［12］Sklar B.数字通信－基础与应用［M］.徐平平，宋铁成，叶芝慧，等译，北京:电子工业出版社，2008:429－432.

［13］Meyr H，Moeneclaey M，Fetchel S.Digital Communication Receivers:Synchronization，Channel Estimation and Signal Processing［M］.New York:Wiley，1998.

［14］Dempster A P，Laird N M，Rubin D B.Maximum likelihood from incomplete data via the EM algorithm［J］.Roy Stat Soc，1977，39(1):1－38.

［15］Aldo N，Andrea D，Mengali U，et al.The modified Cramer－Rao bound and its application to synchronization problems［J］.IEEE Transactions on Communications，1994，42(2):1391－1399.