城市出租车拥挤收费

祝进城，肖 峰，帅 斌，刘晓波

(西南交通大学 交通运输与物流学院，成都610031)

0 引 言

在拥挤收费区域内的出租车是否也应征收拥挤费的问题在不同国家中存在较大的争议。如在新加坡，所有使用拥挤收费区域的出租车都需要缴纳拥挤费;在香港，出租车与私家车相同，当使用海底隧道时，均需要支付通行费;而在伦敦，出租车却享有免收拥挤费的权利。此外，在许多大城市中由于出租车的便捷性使得出租车在出行需求中所占的比例非常高［1－2］。而且，与私家车不同，出租车除拥有大量目的地明确的载客出租车以外，还有数量众多、处于搜寻顾客状态的空驶出租车。这些空驶与载客出租车的运营，占据了大量的道路资源。因此研究出租车的收费政策是拥挤收费实施过程中必须要解决的重要问题。

以往已有很多研究对出租车在路网中的行为和对社会福利的影响进行了建模与分析。如，文献［1，3－7］分析了出租车的服务过程与市场调节本质的关系。文献［8］研究了美国曼哈顿与拉瓜迪亚(LaGuardia)机场之间，拥挤收费对载客出租车路径选择及旅行时间的影响。结果表明，只有时间价值非常高的乘客(大于170 美元/h)才能从该项政策中获益。然而，该论文只分析了拥挤收费对载客出租车的影响，而没有考虑其对私家车及空驶出租车带来的影响。事实上，对出租车进行拥挤收费对整个系统(包括私家车、载客出租车以及空驶出租车)产生的影响有其两面性:一方面，优化的收费费率能够有效地将出租车造成的外部成本内部化，从而减少由于出租车自私的路径选择行为带来的拥挤成本;另一方面，对出租车征收拥挤费会提高其使用成本，导致部分乘客转向运营成本较高的私家车，这将带来系统的效率损失。因此，出租车拥挤收费对社会福利的最终影响需要进一步研究。

本文在实施拥挤收费背景下，构建了多方式分担的双层规划模型来比较对出租车征收拥挤费前后的最大社会福利变化，进而为分析拥挤收费区域的出租车是否也应该缴纳拥挤费问题提供有效的研究方法。

1 下层组合网络均衡模型

1.1 多方式交通网络建模

考虑交通网络G(V，A)，V 为节点集合，A 为路段集合，为收费路段集合，。R 为起点集合，S 为讫点集合。采用上标“p”、“c”、“v”分别表示私家车、载客出租车以及空驶出租车;同时，采用ψ ∈Ψ=(p，с)来表示私家车与出租车的出行方式集合。在任一研究时段，存在以下需求约束条件:

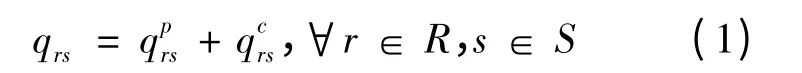
式中:qrs为OD 对r，s 间的总交通需求量为选择私家车的人数;为选择出租车的人数。

载客出租车则满足以下流量守恒方程:

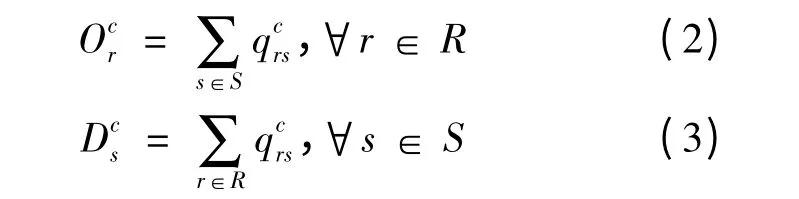
除载客出租车以外，道路上还存在大量搜寻顾客的空驶出租车。在一个稳定的平衡状态下，路网上的空驶出租车能够满足所有用户的需求;同时，每一位用户在经过等待与搜索之后将最终能够得到出租车服务［9］。从而，有以下约束:

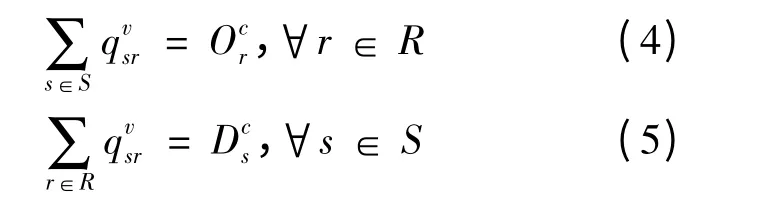
此外，路段a ∈A 上的总流量xa可通过下式计算:

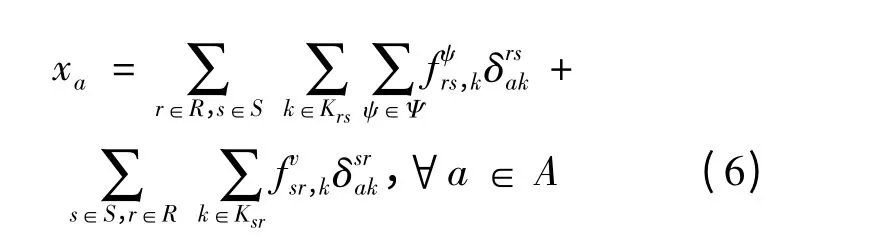
1.2 广义出行费用函数

如果对拥挤收费区域内的出租车征收拥挤费，则当出租车载客时该费用由乘客承担，空驶时由出租车驾驶员承担，从而可得以下路段广义出行费用函数［1，3］。

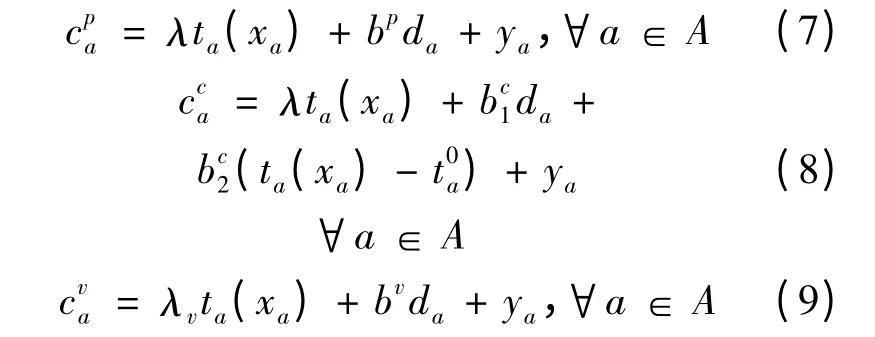
同理，当出租车不需要交纳拥挤费时有:

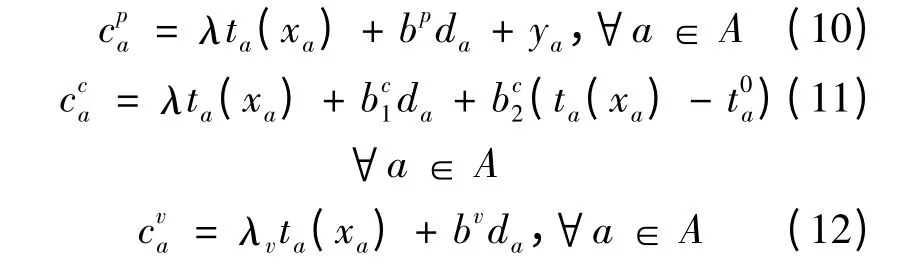
对应的各路径广义出行费用如下所示:

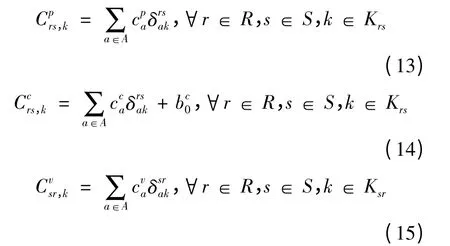
为了便于建模，不考虑出租车和出租车乘客的等待时间。

1.3 路径选择

考虑各交通方式的路径选择问题，根据Wardrop 均衡原理，采用以下数学式来描述用户的均衡状态:

则

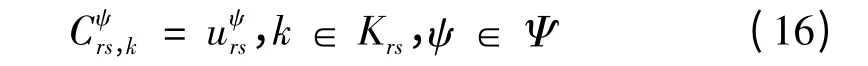
则

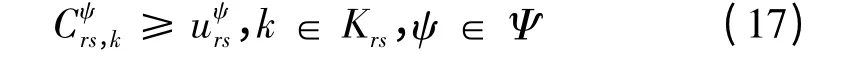
同理，对空驶出租车存在以下条件:

则

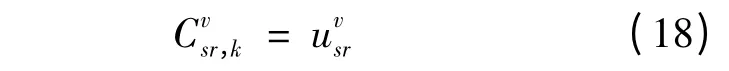
则

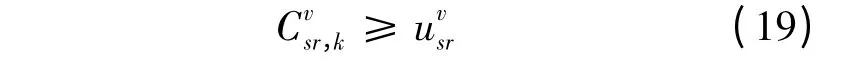
车的最小广义出行费用。

1.4 出行方式选择

采用以下Logit 分离模型来描述出行者的出行方式选择:

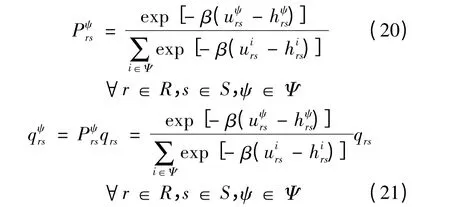
1.5 空驶出租车的交通分布

在拥挤收费政策背景下，无论是否对出租车征收拥挤费，空驶出租车的分布都将受到显著影响。文献［3－5］采用Logit 模型描述了空驶出租车在不同OD 对间的概率分布。文献［4］指出，除Logit 模型以外，机会模型或者熵最大化的分布模型也能描述空驶出租车的交通分布。文献［10］采用基于熵最大化准则的重力模型描述了不同交通方式(包括出租车、私家车与货车等)的交通分布问题，并指出该模型能够有效考虑发生点与吸引点的社会经济因素。故本文采用基于熵最大化准则的重力模型来对空驶出租车的分布问题进行描述:

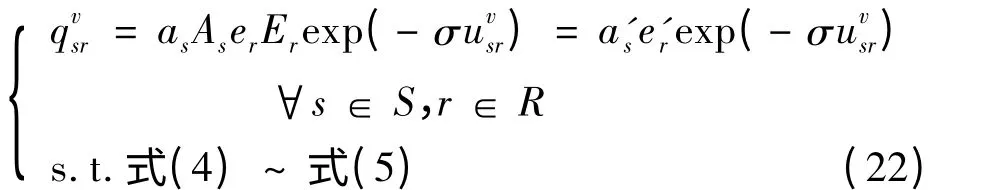
式中:as与er表示与约束条件式(4)(5)有关的拉格朗日因子;As与Er表示与出租车产生及吸引密切相关的外部社会经济变量，其中a's=asAs，e'r=erEr;σ 为自由参数;由于包含as、er、As、Er、σ等参数，上述基于熵最大化准则的重力模型能够有效反应出行决策的行为本质［10］。

1.6 弹性需求

考虑到拥挤收费会显著影响OD 需求量，因此，需求是弹性的，通常可描述为OD 对(r，s)间最小广义出行费用的连续单调减函数。

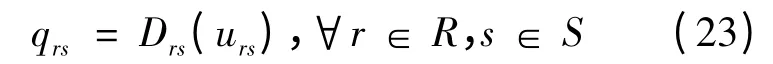
式中:urs为OD 对(r，s)间的最小广义出行费用，可表示为不同交通方式ψ 之间最小广义出行费用的对数形式。

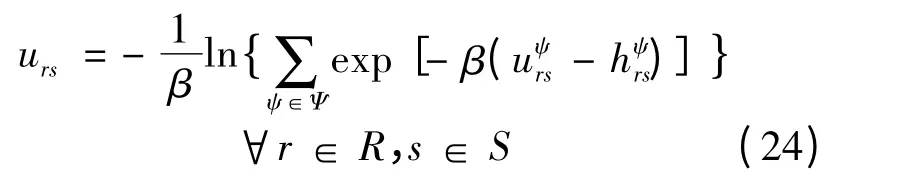
2 等价的变分不等式模型

由私家车与出租车的广义出行费用函数可知，它们的流量相互影响，且这种影响是非对称的，因此，采用变分不等式来描述上述组合网络均衡模型。可行域Ω 如式(25)～(32)所示，括号中为对应的对偶因子。

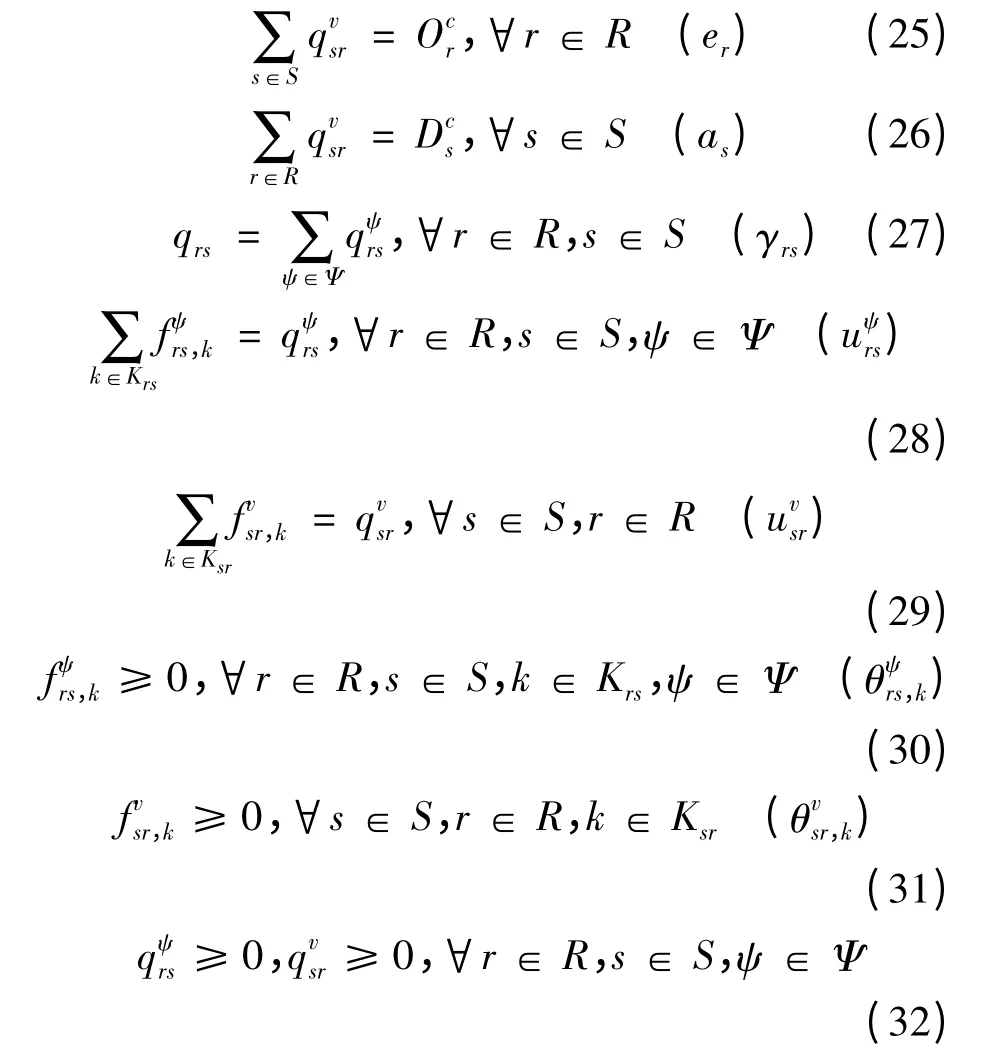
其中，式(25)(26)为空驶出租车起讫点流量守恒条件;式(27)表示OD 总需求的守恒关系;式(28)(29)为路径流量与OD 需求的守恒条件;式(30)(31)(32)为路径流量与需求的非负约束。

在说明相应的约束条件之后，出租车拥挤收费问题的变分不等式模型(P1)可描述为:

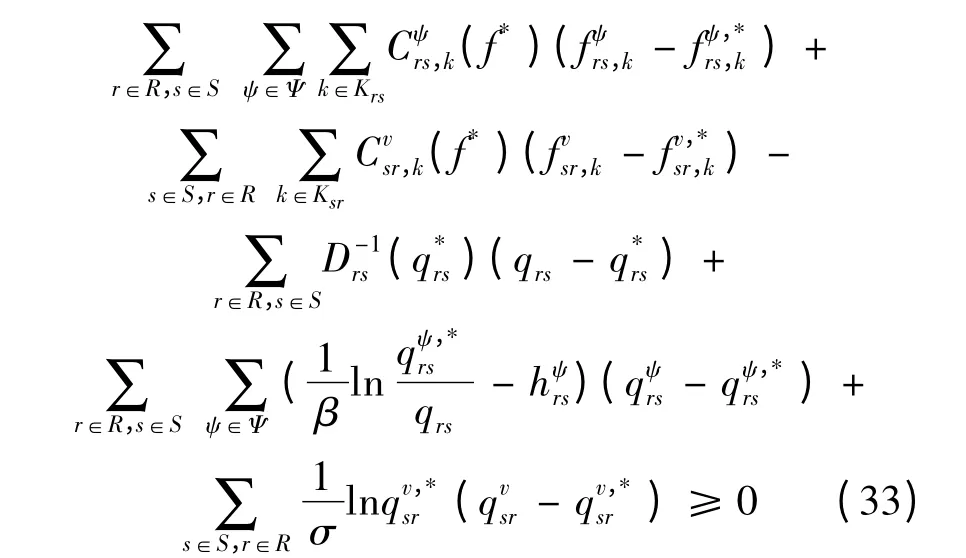
定理1 变分不等式模型(P1)等价于上述组合网络均衡模型。

证明 变分不等式模型(P1)的库恩－塔克条件可表示为:

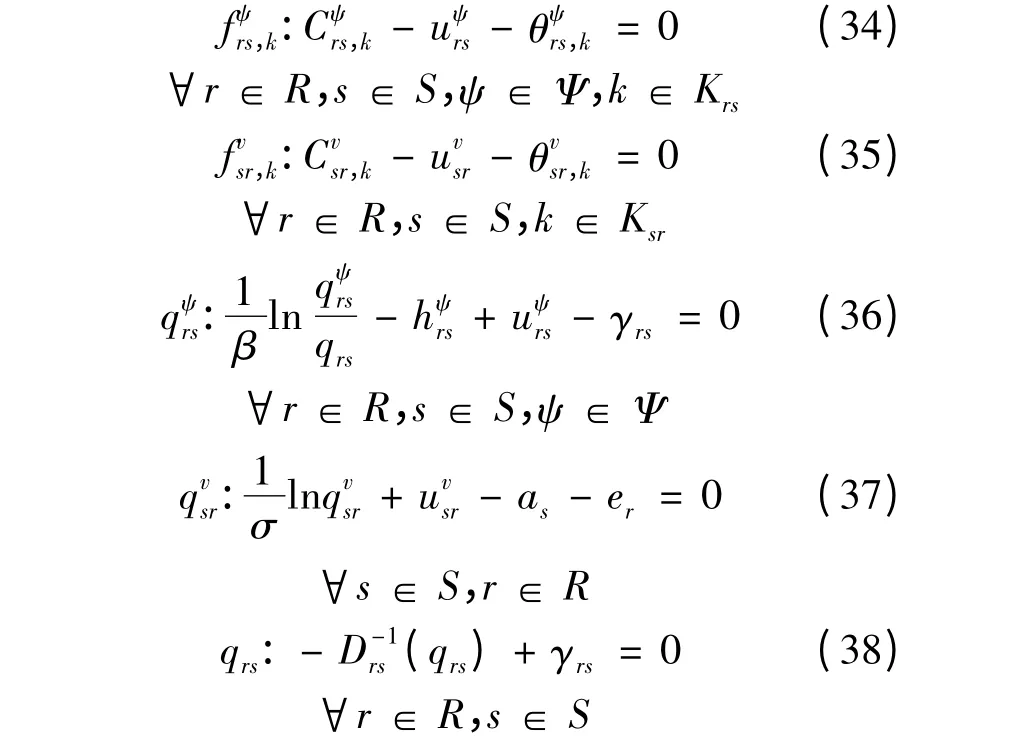
补充约束条件为:

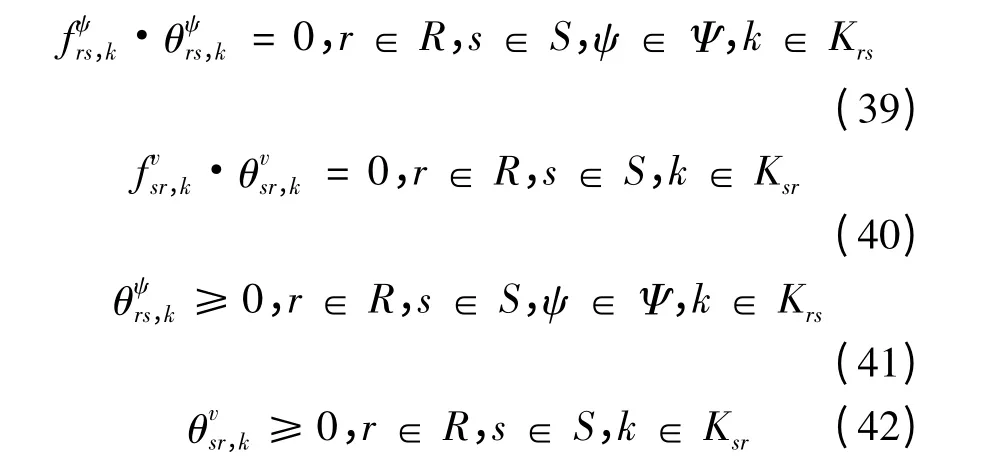
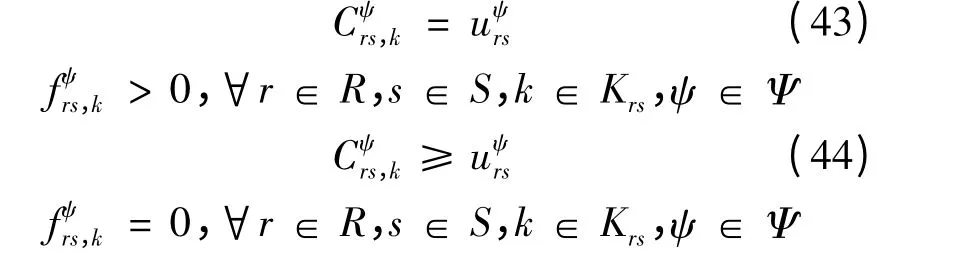
上式说明私家车与载客出租车的路径选择符合UE 准则。同理，通过式(40)(42)和式(35)可证明空驶出租车的路径选择也符合UE 准则。

此外，由式(36)可得:

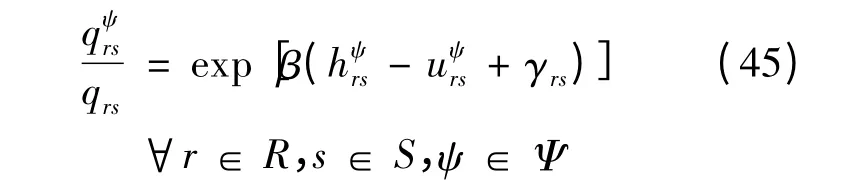
式(45)两边对ψ 求和可得:

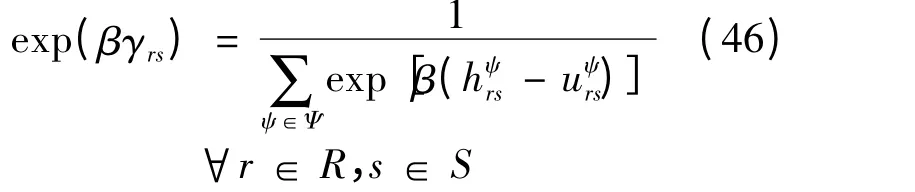
将式(46)代入式(45)可得:

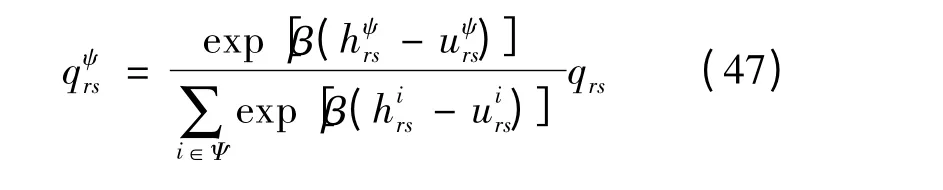
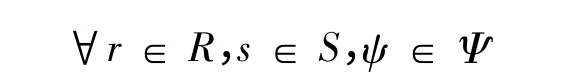
上式即为基于Logit 模型的方式选择式(21)。

根据式(37)可得:

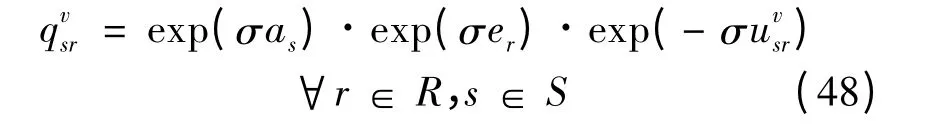
对比式(48)和式(22)可知，exp(σas)与exp(σer)分别等价于a's和e'r，∀r ∈R，s ∈S。

此外，由式(46)可知:

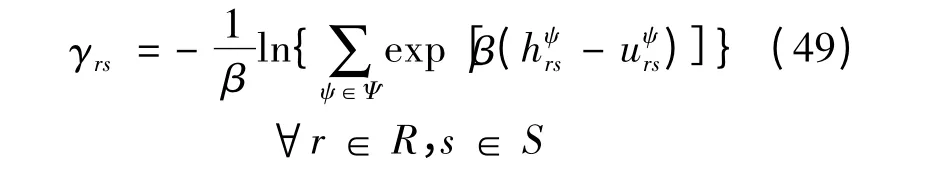
将式(49)代入式(38)可得:

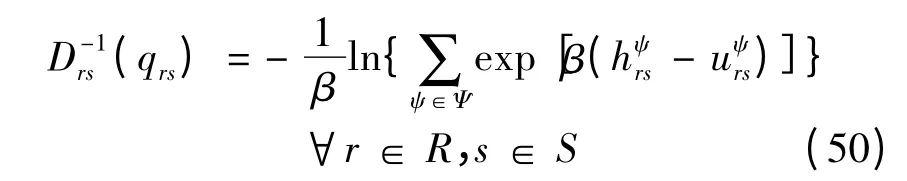
式(49)(50)正好分别是弹性需求式(23)和式(24)。

由于变分不等式模型(P1)的可行域Ω 是由一系列非负、线性约束条件构成的，因此，是紧的凸集;同时考虑到该变分不等式是带有非负流量约束的连续函数，从而至少存在一个解［3］。

3 上层社会福利最大化模型

为了比较在拥挤收费区域内，出租车缴纳拥挤费前后的社会福利变化，同时为了求解最优的拥挤收费费率，上层规划模型(P2)采用社会福利最大化为优化目标。考虑到拥挤收费费用以及乘客支付出租车的费用均属于系统内部转移费用，因此不计入系统成本。

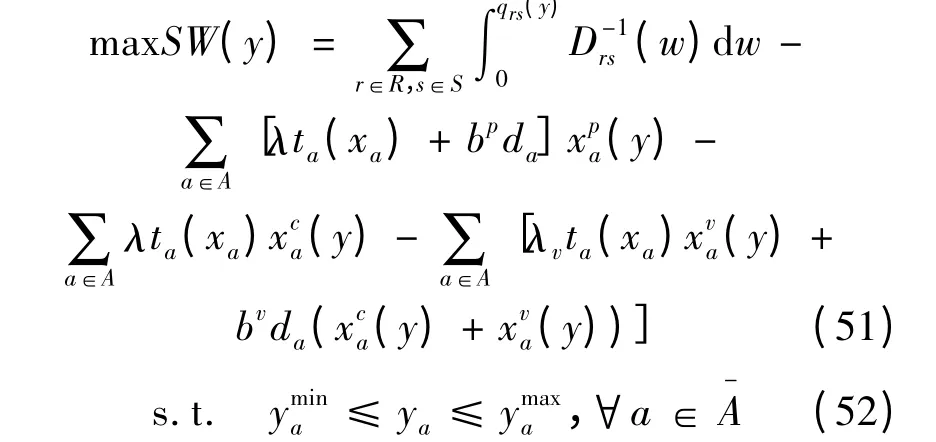
4 求解算法

采用高斯－赛德尔分解法(Block Gauss－Seidel decomposition method)与MSA(Method of successive average)技术相结合的混合算法求解上述变分不等式模型。算法具体步骤如下所示。

步骤1 初始化路段流量。设迭代次数j=0，选一初始可行解，a ∈A，m ∈M。

步骤3 计算需求量。根据步骤2 得到的最小广义出行费用，采用弹性需求函数式(23)计算总的需求量。根据Logit 分离模型式(21)分别计算私家车与载客出租车的需求量。然后采用基于熵最大化准则的重力模型式(22)和式(4)(5)计算空驶出租车需求量，其中起点r ∈R 的出租车发生量与讫点s ∈S 的出租车吸引量由式(2)(3)获得。步骤4 交通流量分配。在获得各交通需求量之后，采用对角化算法求解下列固定需求网络平衡问题，从而得到辅助路段流量，a ∈A，m∈M。

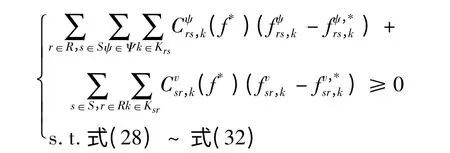
步骤5 采用MSA 技术更新流量。根据下式更新路段流量:

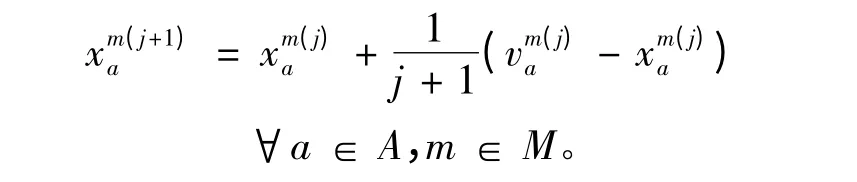
步骤6 收敛性检验。若:

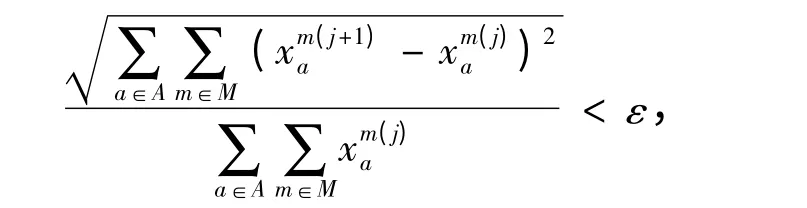
则转步骤7;否则令j=j+1，返回步骤2。

在得到上述变分不等式模型(P1)的解之后，采用遗传算法求解整个双层规划模型。采用二进制编码，约束条件式(52)可通过决策变量的边界设置进行消除。详细的求解过程可参考文献［11－12］。

5 算例分析

算例网络结构如图1 所示，包括(1，6)，(1，4)，(5，6)和(5，4)4 个OD 对，6 个节点，14 条路段。旅行时间函数采用如下BPR 公式:

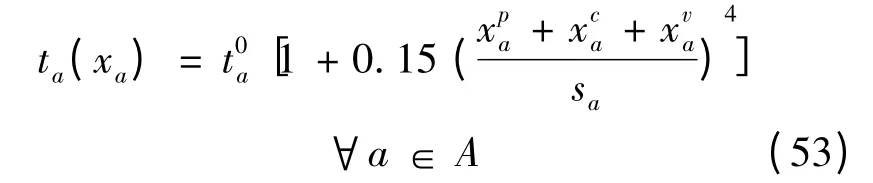
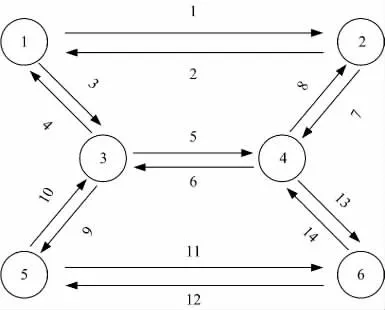
图1 算例网络Fig.1 Example network

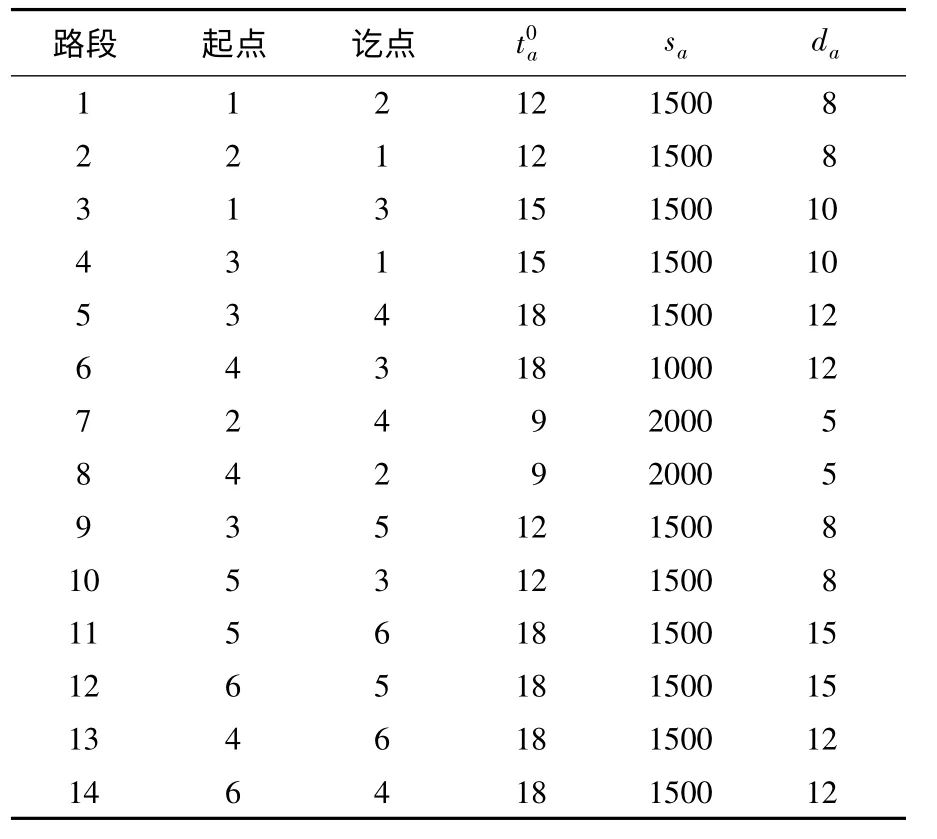
表1 自由流旅行时间和路段通行能力及路段长度Table 1 Link free flow，capacity and length

需求函数采用以下负指数形式:

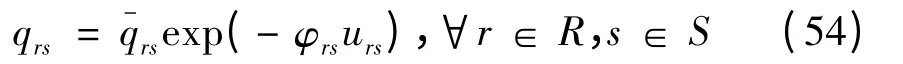
此外，在遗传算法参数选取中，取初始种群大小为20，交叉概率为0.75，变异概率为0.05，最大进化代数为100。

图2 描述了遗传算法的收敛过程。图2 表明，算法在第50 代附近达到了收敛。同时，由图2 可知，出租车拥挤收费后的最大社会福利相对于收费前有明显提高(提高了30.04%)，其中，出租车拥挤收费后的最大社会福利为3.03×105，收费前为2.33×105。导致这一结果的原因为，如果不对出租车进行拥挤收费，则出租车的路径选择行为是自私的，没有考虑其自身带来的外部不经济性，这将导致整个系统的效率损失，且该损失大于由于出租车较低运营成本带来的效益提高，因此，社会福利会下降。

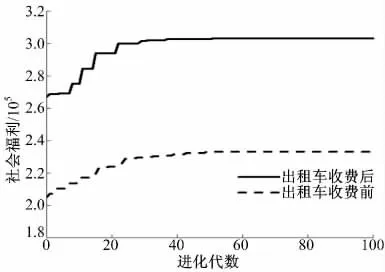
图2 遗传算法收敛图Fig.2 Convergence of the proposed genetic algorithm

表2、表3 以及图3 对出租车拥挤收费前后的系统结果进行了比较。表2 与表3 说明，对出租车征收拥挤费后，私家车的需求量增加了775 veh/h，而出租车的需求量减少了797 veh/h。这是因为，对出租车进行拥挤收费导致其使用成本增加，因此，部分乘客转向了私家车。此外，表2与表3 还说明OD 总需求量受出租车拥挤收费的影响较小，仅减少了22 veh/h。

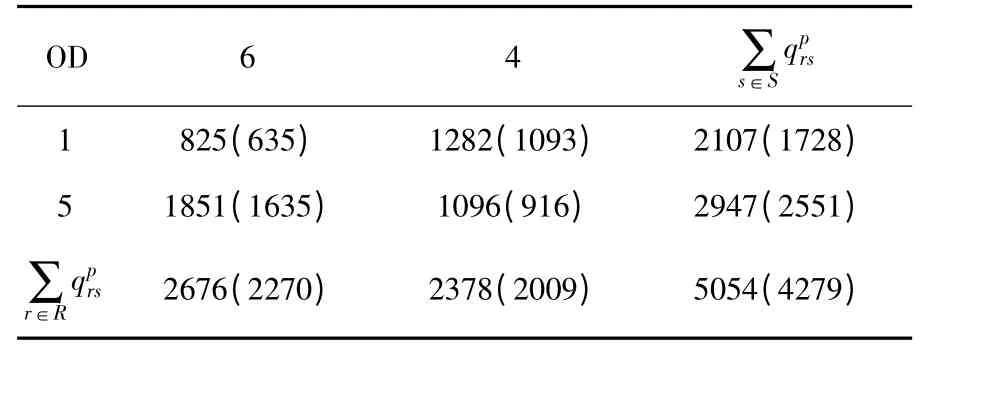
表2 出租车拥挤收费后(收费前)的私家车需求量Table 2 O－D matrix of private car when charging taxi(not charging taxi) veh/h

表3 出租车拥挤收费后(收费前)的出租车需求量Table 3 O－D matrix of taxi when charging taxi(not charging taxi) veh/h

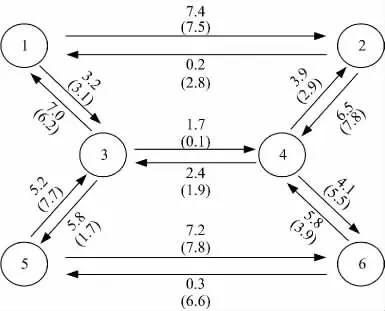
图3 出租车拥挤收费后(收费前)的最优费率Fig.3 Optimal toll when charging taxi(not charging taxi)

图4 为出租车拥挤收费后与收费前的最大社会福利之比(用ρ 表示)与私家车、出租车单位距离运营成本之比(用ω 表示)的关系。图4 表明，随着ω 的增加，ρ 逐渐减小，原因为:对出租车征收拥挤费后，部分乘客转向了私家车，由于私家车的运营成本更高，因此社会成本将增加。所以，ω越大，出租车收费后的社会成本也就越大，从而ρ将越小。此外，从图4 中还可以看出，当ω 大于5.6 时(尽管这不太符合实际)，ρ 将小于1，这说明，此时，出租车拥挤收费后的最大社会福利小于收费前的水平。

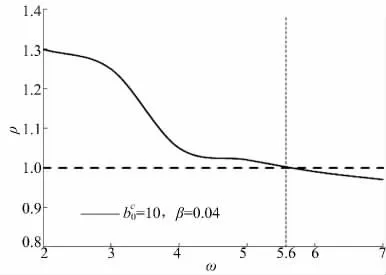
图4 出租车拥挤收费前后的最大社会福利之比与私家车、出租车单位距离运营成本之比的关系Fig.4 Ratio of maximum social welfare for charging taxi to that for not charging taxi versus ratio of operating cost per unit distance for private car to that for taxi

图5 为出租车拥挤收费后与收费前的最大社会福利之比与出租车起步价bc0 之间的关系。图5表明，起初，ρ 随着出租车起步价的增加而剧烈下降。这是因为，出租车使用成本提高，导致其需求量下降，因此，由出租车产生的外部成本也将降低，这使得出租车拥挤收费前后的社会福利变化减小。此外，当出租车起步价超过25 元时，由于其使用成本过高，因此，出租车需求量非常小，对整个系统的影响不明显，所以，ρ 将趋于稳定且接近于1。

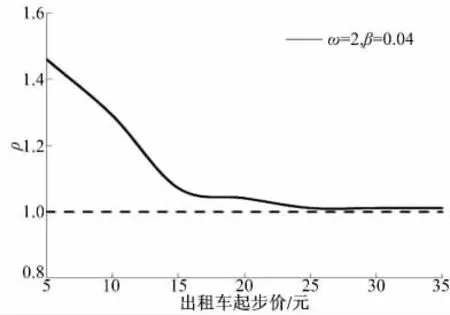
图5 出租车拥挤收费后与收费前的最大社会福利之比与出租车起步价之间的关系Fig.5 Ratio of maximum social welfare between charging and not charging taxi versus preliminary flagfall charge per ride

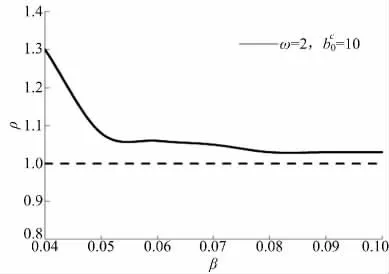
图6 出租车拥挤收费后与收费前的最大社会福利之比与扩散系数之间的关系Fig.6 Ratio of maximum social welfare for charging taxi to that for not charging taxi against dispersion coefficient

图6 为ρ 与扩散系数β 之间的关系。与图5相类似，扩散系数β 也是通过调节出租车需求量来影响ρ 值的变化的，即扩散系数β 越高，出租车需求量越低(该结论是基于出租车需求量通常占总需求量比例小于50%的事实)。因此，扩散系数β 对出租车拥挤收费前后最大社会福利之比的影响与相似。

6 结束语

本文通过构建多方式分担的双层规划模型来研究拥挤收费区域内的出租车是否也应缴纳拥挤费问题。其中，下层规划为等价于变分不等式的组合网络均衡模型。该模型分别描述了出租车拥挤收费前后对出行产生、方式划分、路径选择及出行分布的影响;上层规划以社会福利最大化为优化目标。算例结果表明，私家车与出租车的单位距离运营成本之比是决定出租车是否也应缴纳拥挤费的关键。通常情况下，当二者的比例不是非常大时，对出租车收费后的最大社会福利总是高于收费前的水平。论文的研究为决策者在制定多方式背景下的拥挤收费政策提供了有效方法。未来的研究将考虑公交车方式对系统的影响以及出租车搜寻顾客时间与顾客等候出租车时间对出行方式划分带来的影响，并且下一步的研究还将考虑采用实际采集的数据进行分析。

［1］Yang H，Ye M，Tang W H，et al.Regulating taxi services in the presence of congestion externality［J］.Transportation Research Part A，2005，39(1):17－40.

［2］Salanova J M，Estrada M，Aifadopoulou G，et al.A review of the modeling of taxi services［J］.Procedia－Social and Behavioral Sciences，2011，20:150－161.

［3］Wong K I，Wong S C，Yang H，et al.Modeling urban taxi services with multiple user classes and vehicle modes［J］.Transportation Research Part B，2008，42(10):985－1007.

［4］Yang H，Wong S C.A network model of urban taxi services［J］.Transportation Research Part B，1998，32(4):235－246.

［5］Yang H，Wong S C，Wong K I.Demand－supply equilibrium of taxi services in a network under competition and regulation［J］.Transportation Research Part B，2002，36(9):799－819.

［6］Yang H，Leung C W Y，Wong S C，et al.Equilibria of bilateral taxi－customer searching and meeting on networks［J］.Transportation Research Part B，2010，44(8－9):1067－1083.

［7］Yang H，Yang T.Equilibrium properties of taxi markets with search frictions［J］.Transportation Research Part B，2011，45(4):696－713.

［8］David A K，Jonathan R P.Slow down，you move too fast:the use of tolls by taxicabs in New York city［C］∥Transportation Research Board 91st Annual Meeting，Washington D.C.，2012.

［9］Wong K I，Wong S C，Yang H.Modeling urban taxi services in congested road networks with elastic demand［J］.Transportation Research Part B，2001，35(9):819－842.

［10］Lam W H K，Huang H.A combined trip distribution and assignment model for multiple user classes［J］.Transportation Research Part B，1992，26(4):275－287.

［11］Ge Y E，Zhang H M，Lam W H K.Network reserve capacity under influence of traveler information［J］.ASCE Journal of Transportation Engineering，2003，129(3):262－270.

［12］Zhang H M，Ge Y E.Modeling variable demand equilibrium under second－best road pricing［J］.Transportation Research Part B，2004，38(8):733－749.