微细电火花线切割表面三维粗糙度的结构性参数

郭黎滨，张 彬，崔 海，2，张志航

(1.哈尔滨工程大学机电工程学院，哈尔滨150001;2.哈尔滨工程大学工程训练中心，哈尔滨150001;3.洛阳理工学院 机械工程系，洛阳471023)

0 引 言

与传统切削和磨削加工表面呈规则或周期性纹理特征的各向异性表面不同，微细电火花线切割加工(Micro wire electrical discharge machining，MWEDM)表面是由无数呈随机分布的椭球状凸峰和凹坑组成，属于各向同性表面［1］。在表征三维粗糙度时，表面结构的形状和分布特征对斜率、曲率和等方性等表征参数的计算精度和计算方法会产生很大影响［2－6］。这些主要由表面结构确定的参数可称为表面三维粗糙度的结构性参数，包括空间参数、混合参数和特征参数。

2002 年国际标准化组织ISO/TC213 委员会成立了WG16 工作组，负责研究并制定用于表面三维粗糙度评定的国际标准。经过10 年努力，2012 年正式公布了产品几何技术规范ISO 25178，其中定义了表面结构表征参数，用区域法替代了轮廓法，实现表面三维粗糙度的评定［7－9］。但是，由于传统加工方法在整个机械加工领域所占比重较大，ISO 25178 标准很大程度上适用于传统加工方法的各向异性表面，应用于MWEDM 的各向同性表面时，有的参数没有实际意义，有的参数的计算结果与实际情况不符，有的计算过程复杂。因此，有必要从MWEDM 表面微观三维结构出发，对现有三维粗糙度空间参数、混合参数和特征参数的表征目的和计算方法进行深入分析，研究对于MWEDM 表面的精确表征，最终建立适合各向同性的MWEDM 表面的结构性参数。

1 MWEDM 表面的三维构造

用扫描探针显微镜测量外圆磨削加工表面和MWEDM 表面微观形貌，如图1 所示。通过对比可以看出，MWEDM 表面纹理没有明显的方向性，属于各向同性表面。MWEDM 表面是由无数的随机分布凸峰和凹坑组成的，表面凸峰的形状较为规则，峰顶大多呈椭球形，并且有些距离较近的凸峰呈现出重叠现象。凹坑多呈现不规则形状，从图1 中也可看出凹坑重叠的现象。

2 三维粗糙度空间参数

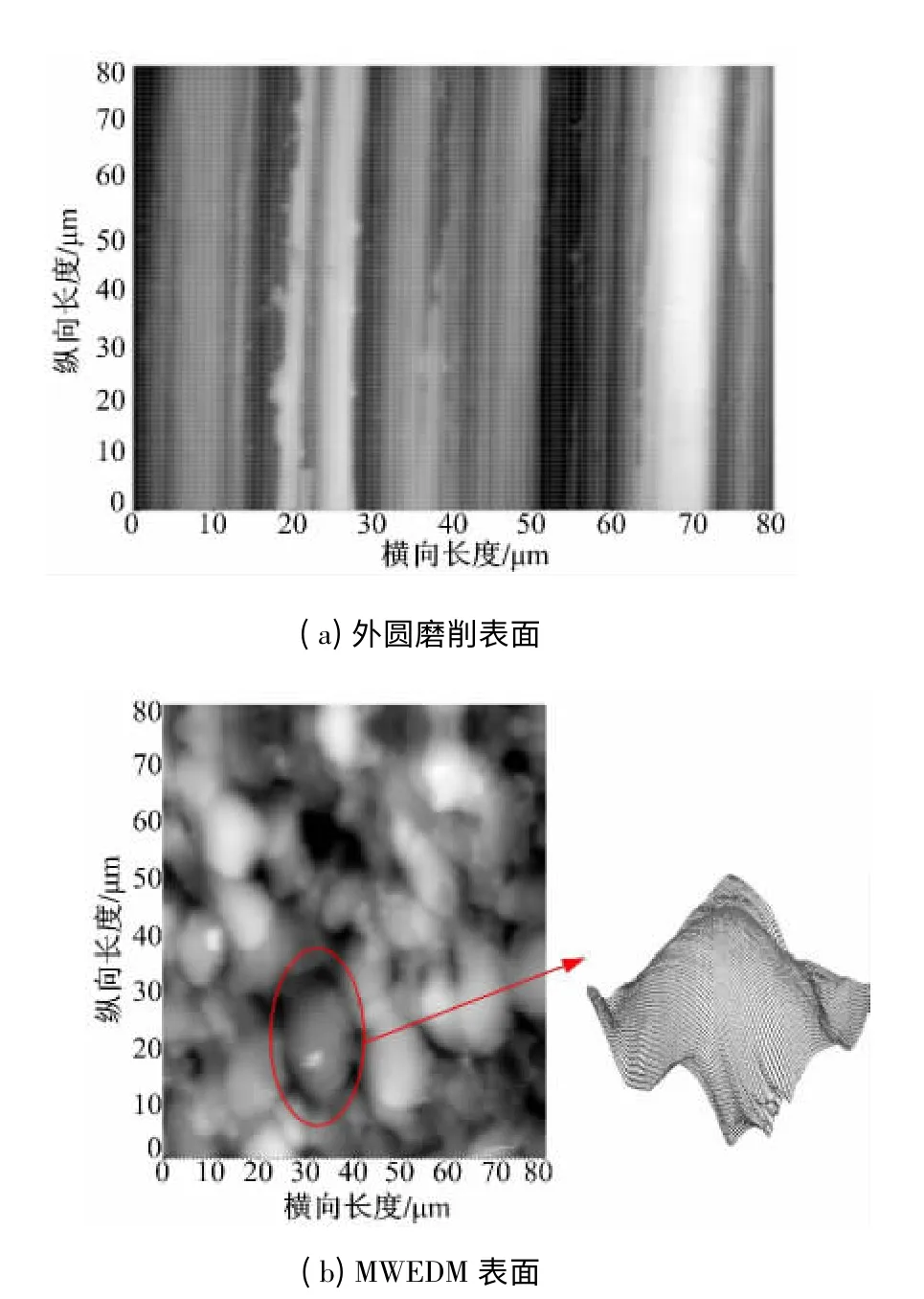
图1 外圆磨削加工表面轮廓和MWEDM表面的凸峰结构特征Fig.1 Surface topography of cylindrical grinding and the structural characteristics of MWEDM surface peak

空间参数主要描述表面的纹理特征，包括纹理疏密和纹理方向等，根据国际标准草案ISO 25178－2 对空间参数的计算方法所做说明如下:

最速衰减自相关长度Sal 定义为对于给定阈值s 有最速衰减自相关函数ACF(tx，ty)的水平距离，表示为:

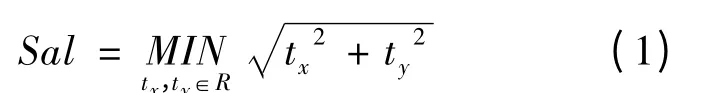
表面的结构形状比率Str 是在相同条件下自相关图上的最小半径和最大半径的比值，表示为:

表面纹理方向Std 是通过二维表面的傅里叶变换后，计算角功率谱得出，表示为:

根据ISO 25178－2 中对空间参数的计算方法所做说明，最速衰减自相关长度Sal 和表面的结构形状比率Str 的计算过程(见图2 所示)如下:

首先如图2(a)所示，计算三维表面的二维自相关函数;其次如图2(b)所示，选取合适的阈值，一般取s=0.2，截取主峰截面;然后如图2(c)所示，分离主峰截面边界;最后如图2(d)所示，把不同方向上的自相关长度转换成极坐标的形式。

图2 Sal 和Str 的计算过程Fig.2 Procedure to calculate Sal and Str

由图2 的计算过程可知，ISO 25178－2 计算空间参数的方法是取表面纹理的两个极值。在各向异性表面中，相当于沿着与加工纹理相垂直和平行的两个方向建立了3 个参数，以最大值的指向作为表面纹理方向，以最小值表示纹理强弱，以最小值和最大值的比值表示纹理密度。但是，MWEDM 表面是纹理复杂的各向同性表面，最大值和最小值仅能代表两个方向上的纹理特征，如图3 和图4 所示。

图3 各向同性表面Fig.3 Surface with an isotropic texture

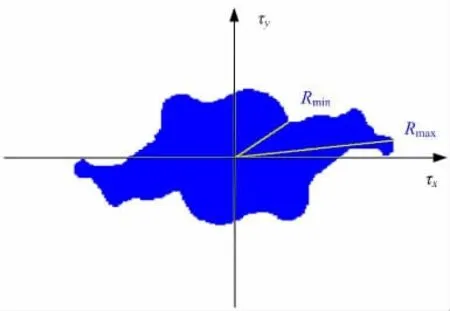
图4 表面二维自相关谱主截面Fig.4 Principal section of 2D autocorrelation spectrum

从图3 和图4 中可以看出，对于各向同性表面，仅用Rmin和Rmax并不能表征表面纹理的复杂程度。为此，应当引入圆形度，通过计算二维自相关谱主截面边缘的圆形度，从而更好地描述各向同性表面纹理的复杂程度，其计算公式为:

式中:S 为主截面的面积;D 为主截面的周长。

对于MWEDM 表面，计算测量表面结构形状比率Str 的方法可以采用二维自相关谱主截面面积与其边界周长的比值。

ISO 25178－2 中表面纹理方向Std 的方法是通过Rmax的两次变换，即通过傅里叶变换成功率谱密度形式，再将功率谱密度变换成极坐标形式。以Rmax的方向角代表表面纹理方向，计算过程复杂。可以直接通过计算二维自相关谱主截面的二阶中心矩得到Rmax，首先计算表面二维自相关谱主截面的二阶中心距:

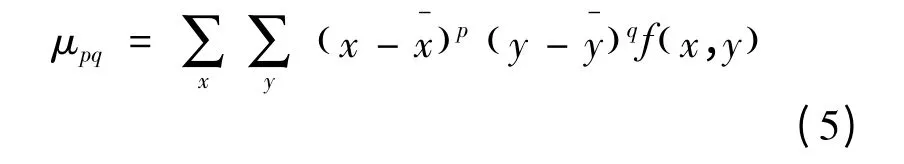
主轴方向角Std 表示为:

ISO 25178－2 中最速衰减自相关函数Sal 主要描述各向异性表面中纹理的宽窄，由于各向异性表面纹理有规则的周期，Sal 可以代表周期的大小;而MWEDM 表面纹理周期是完全随机的，参数Sal 对MWEDM 表面纹理没有实际的表征意义。

3 三维粗糙度混合参数

混合参数包含表面纵向和横向信息。评定参数有:表面均方根梯度Sdq，Sdr 和Ssc。说明如下。

表面上点的梯度对于x 和y 轴分别被定义为∂z/∂x 和∂z/∂y，整个表面上均方根梯度计算表示为:

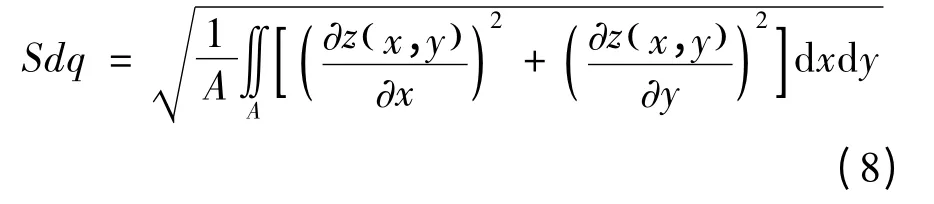
式中:A 代表定义区间，这里指MWEDM 表面粗糙度的评定面积。

表面的展开界面面积比率Sdr。可以是无单位的正数或百分比，它通常介于0 ～10%，一个完全平面和光滑的表面Sdr=0%。

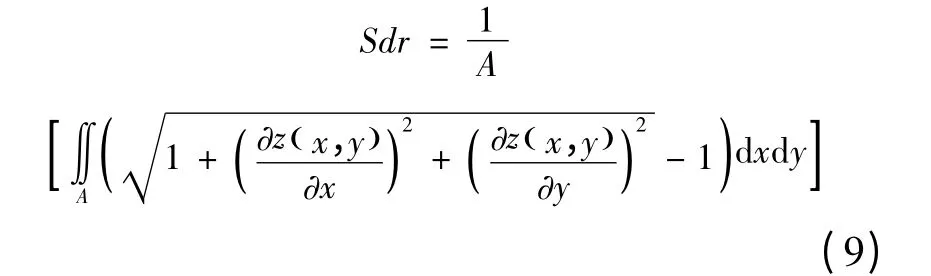
表面算术平均顶点曲率Ssc:

式中:n 为表面凸峰的数目。

混合参数的计算精度依赖于表面测量方向，对具有规则纹理的各向异性表面可以通过规定测量方向提高计算精度。而对于纹理复杂的各向同性表面，现有的计算参数无法有效解决这一问题。

图5 中，FGx 和FGy 分别表示外圆磨削表面沿与纹理垂直和平行两个方向上斜率的统计概率曲线，其方差分别为σx=10.1843，σy=51.7574;FMx 和FMy 分别表示MWEDM 表面在X 向和Y 向上斜率的统计概率曲线，其方差分别为σx=35.0235，σy=33.2908。从图5 中可知，当MWEDM 表面斜率的正态分布取μ±σ 时，相当于外圆磨削沿X 向测量的μ±3σ。也就是说，在二维粗糙度测量中，当外圆磨削表面斜率的测量精度达到99%以上时，MWEDM 表面斜率的测量精度只有70%。

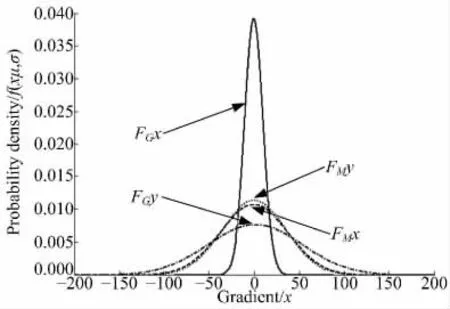
图5 两种表面X 向和Y 向斜率的概率密度Fig.5 Slope probability density of MWEDM and cylindical grinding surface

由式(8)～式(10)可知，斜率是计算混合参数的基础，其计算精度严重影响混合参数的表征精度。为此，可以引入微分几何的曲面论，通过曲面的两类基本量计算MWEDM 的曲率。

设被测的MWEDM 表面为z=z(x，y)，其中x、y 为该点在图像矩阵中的坐标。则MWEDM 表面的第一类基本量为:

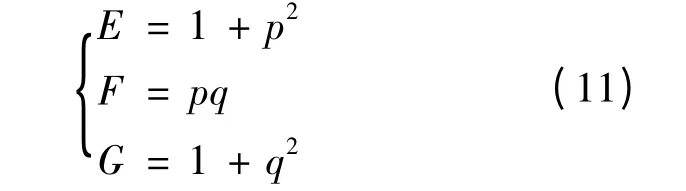
MWEDM 表面的第二类基本量为:

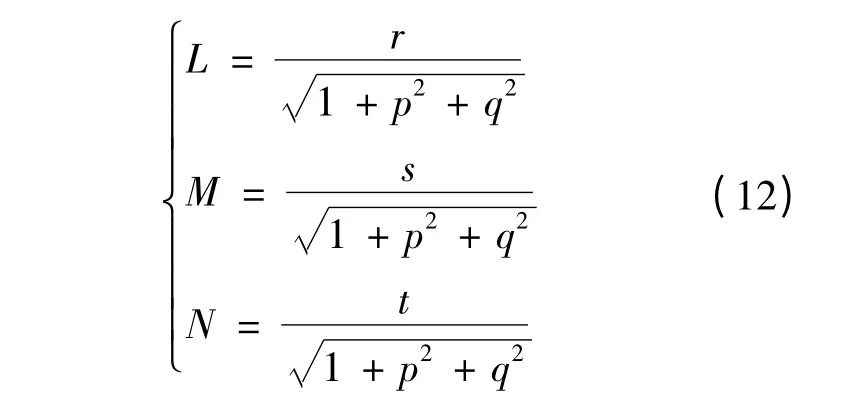
通过Weingarten 公式有:

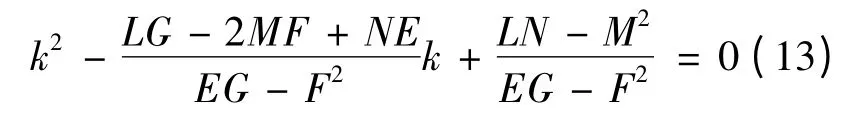
根据曲面曲率的定义可知，平均曲率为H=(k1+k2)/2，高斯曲率为K=k1·k2，由根和系数的关系可得:

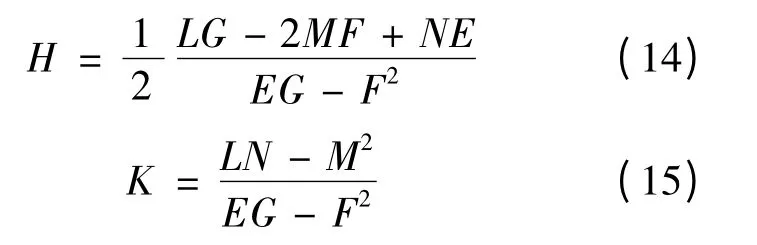
由式(14)可知，ISO 25178－2 中用平均曲率描述加工表面峰的曲率特征，基于此，通过式(11)～式(15)计算MWEDM 表面峰的平均曲率，结果如图6 所示。

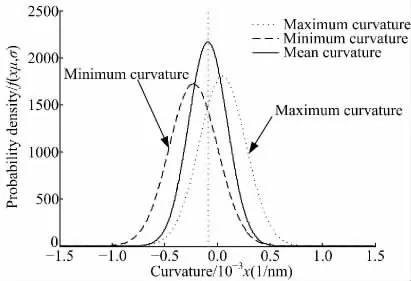
图6 表面凸峰的主曲率和平均曲率的概率密度曲线Fig.6 Principal curvature and mean curvature probability density of the MWEDM surface peak

从图6 中可以看出:MWEDM 表面凸峰的平均曲率小于零，计算结果表示MWEDM 表面凸峰为凹的，这与凸峰实际特征不符。究其原因可知，平均曲率只能表征柱状结构的凸峰曲率，而MWEDM 表面凸峰是椭球状的，用高斯曲率进行表征更为准确。由式(15)计算MWEDM 表面凸峰的高斯曲率，结果如图7 所示。

图7 为MWEDM 表面凸峰高斯曲率的概率密度曲线，其均值和方差分别为:μ=5.0151×10－9，σ=1.0716×10－7。由此可知，用高斯曲率表征MWEDM 表面凸峰曲率计算精度很高，且与表面凸峰实际特征相符。

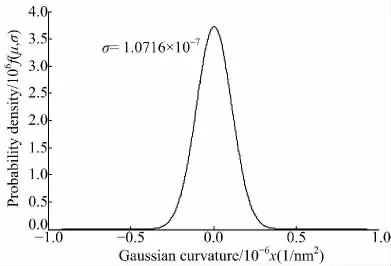
图7 表面凸峰高斯曲率的概率密度曲线Fig.7 Gaussian curvature probability density of the MWEDM surface peak

4 三维粗糙度特征参数

特征参数是基于包络制提出的评定参数，注重对表面凸峰和凹坑特征的评定。经过小波基准面分离后的MWEDM 表面，削弱了低频成分对3D－Motif 合并准则的不良影响，采用分水岭算法能够更加准确分割表面凸峰和凹坑，从而确定表面结构中凸峰和凹坑的数目，如图8 所示。

图8 用分水岭算法分割表面凸峰Fig.8 Watershed algorithm to partition the MWEDM surface peak

基于分水岭算法提出以下参数。

表面峰密度Spd:

式中:N 为评定面积上凸峰的数目，通过分水岭算法确定。

表面10 点高度S10z:

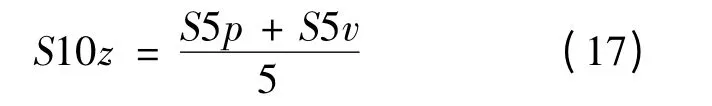
式中:S5p 代表表面5 个凸峰的高度值;S5v 代表表面5 个凹坑的深度值。

表面凸峰的平均面积Sha:

式中:表面峰区所占面积是通过分水岭算法提取的表面凸峰区域的面积。

表面凹坑的平均面积Sda:

式中:表面坑区所占面积是通过分水岭算法提取的表面凹坑区域的面积。

ISO 25178－2 中还定义了算术平均峰值曲率(Spc)、5 峰高度(S5p)、5 坑深度(S5v)、峰区体积(Shv)、坑区体积(Sdv)5 个特征参数。由于各向同性表面的纹理方向不明显，Spc 不能准确地表征表面纹理的复杂程度，S5p 和S5v 单独计算峰、坑幅值时，其有效性受表面低频部分的影响很大，不适合用于MWEDM 表面的表征，应予以去除。体积参数Shv 和Sdv 在功能参数中已有表征参数，为了避免参数膨胀也可以去除。

5 结 论

(1)对空间参数Str 和Std 的算法进行改进，用二维自相关函数主峰截面的圆形度来表征表面纹理的复杂程度，提高表征精度;引入二阶中心矩，在主峰截面上直接计算表面纹理的主方向，简化计算过程;去掉对于各向同性的MWEDM 表面没有实际表征意义的参数Sal。

(2)提出用表面凸峰的高斯曲率取代平均曲率来表征MWEDM 表面，使混合参数的计算不再受测量方向的限制，提高计算准确性和精度。

(3)采用分水岭算法分割MWEDM 表面几何要素，可以实现表面凸峰数目的准确计数。特征参数由9 个精简为适合表征MWEDM 表面的4 个参数。

改进后的三维粗糙度的结构性参数可以更准确地表征各向同性的MWEDM 表面，且参数更加简化。

［1］Zhang Zhi－hang，Guo Li－bin，Cui Hai，et al.Surface texture evaluation of micro－WEDM［J］.Applied Mechanics and Materials，2012，138－139:1251－1257.

［2］Balakrishnan N，Scarpa B.Multivariate measures of skewness for the skew－normal distribution［J］.Journal of Multivariate Analysis，2012，104(1):73－87.

［3］Rosenholtz R，Malik J.Surface orientation from texture:isotropy or homogeneity(or both)?［J］.Vision Research，1997，37(16):2283－2293.

［4］Blatevron F.New 3D parameters and filtration techniques for surface metrology［DB/OL］.［2013－05－03］.http://www.doc88.com/p－9763785399764.html.

［5］Scott P J.Feature parameters［J］.Wear，2009，266(5－6):548－551.

［6］Ding Hai－juan，Guo Li－bin，Cui Hai.Statistical characteristic and parameter characterization of 3D surface micro－topography on micro－EDM［C］∥IEEE International Conference on Automation and Logistics，Shenyang，2009:1094－1098.

［7］Schmähling J，Hamprecht F A，Hoffmann D M P.A three－dimensional measure of surface roughness based on mathematical morphology［J］.International Journal of Machine Tools and Manufacture，2006，46(14):1764－1769.

［8］Dapkunas S J.Surface engineering measurement standards for inorganic materials［EB/OL］.［2013－05－29］.http://www.docin.com/p－285097873.html.

［9］Váradi K，Palásti－Kovács B，CzifraÁ，et al.3D characterization of engineerine surfaces［C］∥Proceedings of Polytechnic Jubilee Conference，Budapest，2004:4－5.