复杂制造系统中加工批量的决策
2015-06-12刘红雷周炳海
□ 刘红雷 □ 周炳海
同济大学 机械与动力工程学院 上海 200014
近几十年,随着JIT生产系统在装备制造业的推广应用,其在减少库存、缩短生产提前期[1]方面起到了不可忽视的作用。本文以服务器外壳的制造过程为案例,运用排队论的相关理论,参考复杂制造型企业中生产调度的相关思路[2],计算出合理的加工批量,以达到缩短生产周期、减少在制品的效果。
不同的订单加工批量对生产系统会产生不同的影响,加工批量在一定程度上决定了车间的运行效率和快速响应能力[3]。因为订单的加工批量是影响订单生产周期时间的关键因素,也是影响换型成本在总成本中占比的直接因素。本文不仅研究了订单加工批量在换型成本和总成本的比率中的影响,还根据排队论的相关算法计算出比较合理的加工批量,但是由于数学计算方法本身的局限性及生产过程的复杂性,所以只能取得近似最优解。
基于以上内容,按照服务器外壳零件的实际生产情况,得出一个比较合理的订单加工批量,从而缩短生产提前期,并且减少了换型成本在总成本中的影响。
1 数学模型的建立
本文研究的是服务器外壳零件的加工过程,客户每月需求2 450台,每80台为一个包装单元,工厂每月工作28天,装配线每天可利用的工作时间为9 h,不包含吃饭及休息时间,由此得出客户需求节拍:28×9×60/2 450=6.17 min。另外总装车间的生产效率为92%,所以总装车间生产线设计的节拍时间为:6.17 min×92%=5.67 min。
服务器外壳的金属零件由零件车间(见图1)加工,并供应给工厂内所有的装配线,每天生产两班。服务器外壳的加工过程包含转塔冲、攻丝、冲压、折弯、打磨、压铆等工序(见表1)。
假设生产订单连续,零件车间按加工工艺进行生产,总装车间按客户需求来装配。其中从冲压到压铆2是零件加工工艺流程,每天开两班,装配1到装配2是总装车间的工艺流程,每天开一班,装配1、装配2的产出是根据5.67 min的节拍时间来设计,零件车间的节拍时间是根据产品自身的特性及设备性能来决定。

表1 服务器外壳的加工工序

▲图1 零件加工车间
生产车间目前每个加工批量为80,不考虑工序间的周转时间,假设每个订单到达下一工序后就开始生产,得出的数据如下。
(1)零件由转塔冲到压铆2的生产周期时间计算见表2。

表2 转塔冲至压铆2的生产周期时间
按照理论计算得出生产周期时间为2 000 min,每天开两班,每班上班时间为10.5 h,每班有效工作时间为 9 h,则理论周期天数为:(2 000/60/9/2)=1.85天。
(2)装配1到装配2的周期时间计算见表3。

表3 装配1到装配2的周期时间
总装车间从装配1到装配2的生产周期时间为1 470.2 min,如果以5.67 min的节拍时间来计算,理论生产周期时间为:80×5.67/60/9+7×80/60/9+80×5.67/60/9=2.72天。
综上所述,从下订单开始生产到装配完成,理论上总的周期时间为:(2 000+1 470.2)/60=57.83 h。
1.1 换型成本最低
根据周期时间的计算公式可以看出,转塔冲到压铆2的加工批量越少,其周期时间越短,但是加工批量越少,相同数量的产品、换型的次数及周转的频次也就越高,造成很大的浪费,所以应结合最小经济批量来定义最优化的加工批量。
按照产品某一加工批量X在生产过程中的各项成本数据(见表4),计算出换型成本相对于总的加工成本最低,求得当换型成本(各成本因子总和)最低时,零件在各个工序间的加工批量,并得出了在一定需求条件下的加工批量曲线,如图2所示。
管理成本表示每小时每个工序的成本,包括机器折旧、厂房面积分摊、水电消耗以及模具损耗等费用。
利用数学方法得出 (换型成本)/(总加工成本)的比值Z最小,设定加工批量为X,则计算公式为:

表4 某加工批量生产中的各项成本数据
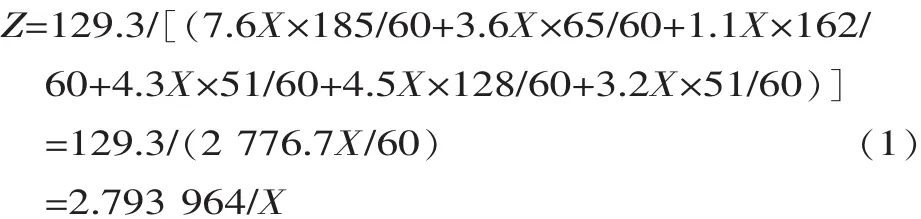
根据以上计算公式得出变化趋势图 (见图2),可以看出在加工批量大于50以后,Z值变化趋于缓慢。
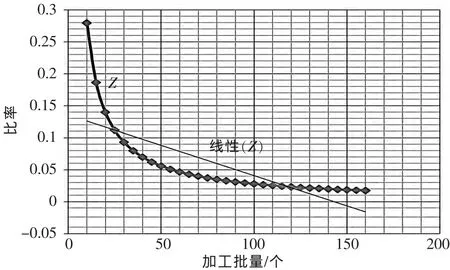
▲图2 在一定需求条件下的加工批量曲线
1.2 最优生产批量的确定
结合排队论的相关理论,参考多品种小批量[4]的研究思路,将实际生产过程中加工任务的到达简化为相应的排队模型,在这样的一个系统中,系统的入口处是按照稳态泊松过程达到的各品种加工任务,按照先到先加工的规则排队(FCFS),系统内部是一个加工中心,对到来的加工任务进行加工。各个加工任务的加工时间相互独立,服从相同的负指数分布。下面建立使生产提前期最小的多品种小批量生产模式下单个品种的生产批量模型[6]。
先设定:Q为使生产提前期最小的多品种小批量生产模式下单个品种的生产批量;a为加工中心加工不同品种任务时发生的设备调整时间的平均值;t为不同品种单位产品加工时间的平均值;D为在每个加工任务期T内的外部总需求量;1/λ为各品种加工任务到达时间间隔的平均值;μ为加工中心在单位时间内可以加工的产品品种数量;1/μ为一个产品品种加工任务的平均加工时间。
由以上定义的各个参数可知:

产品品种的到达率:

从而加工中心的利用率为:
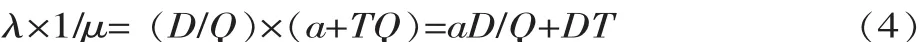
根据排队论中顾客在队中的逗留时间,可推及一个产品品种的等待加工时间与被加工时间,即生产提前期为:
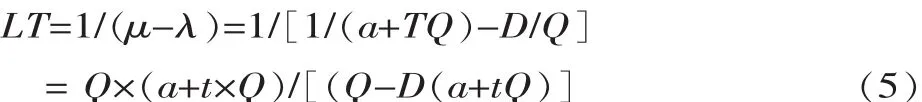
对上式求导数,令其导数为0,则提前期最小的情况下生产批量为:

根据以上公式得出生产周期时间最短的加工批量Q≈42。
2 结束语
考虑设备能力、换型时间、每台设备的管理成本等因素,结合实际生产中每张原材料生产6个零件的限制条件,参考本文1.2节排队论计算得出提前期最小的情况下加工批量为42,以及本文1.1节中在考虑换型成本因素的情况下,加工批量在大于50后趋于平稳,加工批量对总成本的影响不明显,综合考量以上两个方面,将加工批量设定为54,即每个加工订单在第一个工位生产9张原材料,这样既使管理成本比较低,也满足了生产提前期较小的条件。
客户某一批订单为160台,订单为连续生产,即后续生产订单按照零件加工时间最长的转塔冲为节拍时间计算,则根据本文计算的加工批量54及目前的生产加工批量80,两种生产模式得出的对比数据见表5。

表5 两种生产模式的对比
从表5中可以看出,每批零件加工的生产周期时间由43.7 h减少到37.5 h,虽然换型成本在总加工成本中占比由0.82%上升到1.11%,但是相对企业来说,生产周期时间的降低不仅可以降低库存金额,还可以提高企业对客户的反应速度,提高客户满意度。由此造成换型时间的增加可以通过快速换模来解决,这样才可以不断提高企业的竞争力。
复杂制造系统中加工批量的决策受诸多因素影响,是一个多因素决策问题,将简单的数学模型应用于生产调度的决策,使问题更加直观,增强了方案的说服力。在综合考虑换型成本、加工周期两大因素影响的情况下,对企业生产加工批量进行模型计算,得出一个最优解,这样可以为其它大型机械加工企业在生产调度决策时提供理论依据和方法借鉴。
[1] Karmarkar U S.Lot Sizes,Lead Times and In-process Inventories [J].Management Science,1987,33 (3):409-418.
[2] 安进.车间生产批量优化调度研究[D].南京:南京航空航天大学,2005.
[3] 谢祥添.多品种小批量订单式生产系统优化研究 [D].广州:广东工业大学,2008.
[4] 张德胜.多品种小批量机械制造企业MES的研究[J].控制工程,2005(5).
[5] Zinovy D Radovilsky.A Quantitative Approach to Estimate the Size of the Time Buffer in the Theory of Constraints [J].International Journal of Production Economics,1998,55 (2):113-119.
[6] Zipkin P H.Models for Design and Control of Stochastic Multi-item Batch Production Systems [J].Operations Research,1983,34(1):91-104.
