面向可靠性的某型水下机器人耐压壳体设计
2015-06-12赵嘉媛
□ 赵嘉媛
湖北三峡职业技术学院 机电工程学院 湖北宜昌 443002
我国是一个海洋大国,随着海洋资源的日益开发、海洋权益日渐重要。由于海洋水下环境恶劣,人类及水面船只的潜水深度有限,水下机器人(Unmanned Underwater Vehicle,UUV)已成为开发海洋的重要工具,由于其自主性、使用灵活性得到了广泛的应用,它能够完成水下目标探测与识别、海洋资源勘探、海洋环境数据收集、水下救援等,在民用和军用等领域受到越来越多的重视。耐压壳体是UUV最重要的组成部分之一,它是UUV各功能设备的装载平台,为UUV提供所需浮力以及为各功能设备提供一个耐水压的密封空间。因此,耐压壳体的可靠性设计水平直接关系到UUV的安全与任务完成的成功率。
目前UUV耐压壳体的设计大多采用传统安全系数法设计,很少从可靠性角度进行详细设计与计算。本文应用可靠性设计理论中的应力-强度干涉模型,在UUV耐压壳体的强度计算中考虑工作应力和材料强度的离散性,结合机械设计强度理论,基于可靠性设计方法计算了耐压密封相关的设计参数,可有效减轻壳体厚度以减轻质量,增加UUV浮力,成为高可靠的耐压壳体。
1 应力-强度干涉模型
应力-强度干涉模型是目前系统或零件的概率法设计和可靠度计算的重要模型之一[1]。为简化计算模型结合实际情况,耐压壳体应力s和强度δ均为随机变量,且服从正态分布,则根据正态分布函数,应力s和强度δ的概率密度函数可由式(1)、式(2)表示:
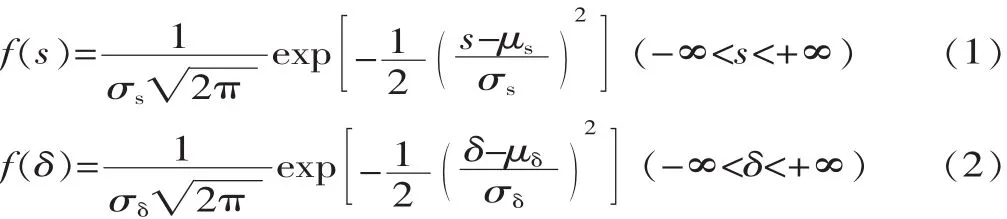
式中:μs、σs为应力 s 的均值与标准差;μδ、σδ为强度 δ的均值与标准差。
令y=δ-s,根据正态分布特性,y也是正态分布,其均值 μy=μδ-μs、标准差 σy=,变量y的概率密度函数为:
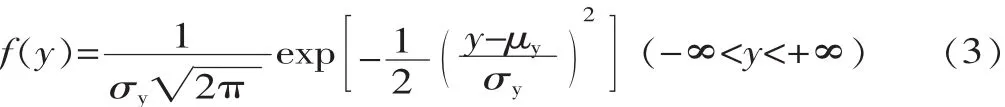
则零部件可靠度R为:
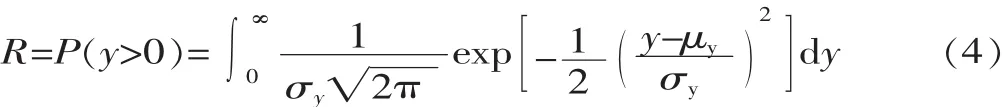
式中:P为概率函数。
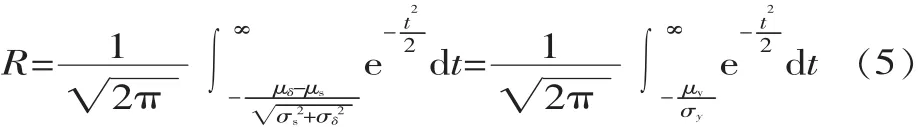
由式(5)可知,在知道应力分布参数、强度分布参数后即可计算出可靠度,它是应力-强度干涉模型中可靠性设计的基本公式。根据标准正态分布的对称性,可将式(5)转换成:,β 称为可靠性系数, 则 R=f(β),即在 μs、μδ、σs、σδ均确定后即可计算出可靠性系数 β,而β与R的对应关系可查相关正态函数表[2]。
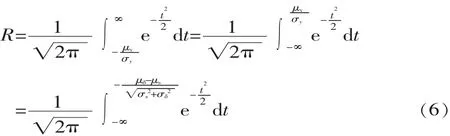
2 耐压壳体强度可靠度计算方法
2.1 耐压壳体应力均值计算
根据压力容器的应力计算公式,计算耐压壳体厚度x,它与材料屈服强度的关系为:

式中:p为设计耐压值;R=267 mm为圆柱壳体半径;σδ0=160 MPa为铝合金材料5A06的屈服强度。
根据式(7),应用基本函数法可得耐压壳体圆柱段应力均值:

式中:μp为实际使用过程中应力均值,μp=3.0 MPa;μR为耐压壳体半径均值,μR=267 mm;μx为耐压壳体厚度x的均值,即设计所需耐压壳体壁厚值。
2.2 耐压壳体应力的标准差计算
根据式(7),应用基本函数法可得耐压壳体圆柱段应力标准差:

式中:σp为实际使用过程中的应力标准差,取压力偏差的1/3;σR为耐压壳体半径的标准差;σx为耐压壳体厚度的标准差,取壳体制造材料钢板壁厚标准差:钢板偏差数值的1/3[3], 设计时为简化, 取 σR=σx=0.2/3=0.067 mm。
2.3 耐压壳体强度均值及标准差
强度均值取所选材料的屈服极限,则 μδ=σδ0,由文献[4]得:σδ=0.07σδ0。
3 设计实例
某型UUV耐压壳体根据项目总体设计要求,耐压壳体两端为球形、中间为圆柱筒体结构。根据使用环境及耐腐蚀要求,壳体设计材料选型为高强重比的铝合金材料(5A06),设计要求耐压值:μp=4.0±0.3 MPa,壳体直径534 mm,圆柱筒体壳体长度800 mm,圆柱段可靠度分配值 0.999 99,即失效率 F=10-6。
已知:p=4.0 MPa,μp=4.0 MPa,σp=0.1 MPa;R=267 mm,μR=267 mm,σR=0.2/3=0.067 mm;σδ0=160 MPa,μδ=σδ0=160 MPa, σδ=0.07σδ0=11.2 MPa,σx=σR=0.067 mm。
由式(6)可知:
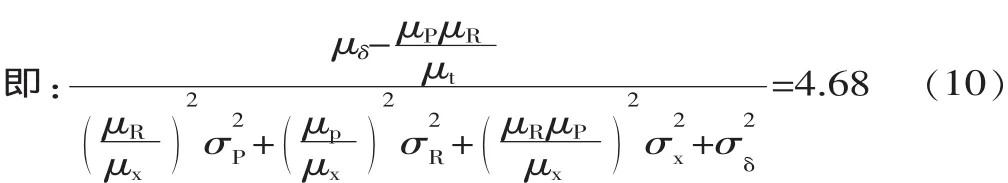
将相关参数代入式(10),计算得 μx=9.9 mm,即耐压壳体壁厚为9.9 mm时可满足设计任务中可靠度0.999 99的要求。
4 结论
本文以某型UUV耐压壳体为例,应用可靠性应力-强度干涉模型,说明了耐压壳体可靠性设计方法的应用。经过该型UUV多次试验,其耐压壳体未发生一次故障,证明了所介绍的可靠性设计方法的有效性,有力保障了UUV的可靠性、安全性。
[1] 张洪才.应力-强度干涉模型的可靠度计算方法的研究[J].机械设计,2001(6):45-47.
[2] 陈钟毓.在用钢制压力容器筒体强度可靠性分析[J].化学工程与装备,2008(7):58-61.
[3] 农琪,谢业东.压力容器椭圆形封头的可靠性设计[J].装备制造技术,2010(9):53-60.
[4] 刘惟信.机械可靠性设计 [M].北京:清华大学出版社,1996.
