一种新型三维力/力矩传感器的研制

2015-06-12张世兴

机械制造 2015年5期

□ 崔岩 □ 张世兴 □ 崔泽

1.齐重数控装备股份有限公司设备保障部黑龙江齐齐哈尔 161005

2.上海大学机电工程与自动化学院上海 200072

多维力传感器作为能够为机器人提供重要的外部力和力矩信息的传感器，在机器人研究中有着广泛的应用。目前，市场上已经有很多种成熟的多维力传感器产品出售，如美国ATI公司的系列六维力传感器产品等［1］。同时，研究人员也根据不同的用途研制了不同类型的多维力传感器，杨磊［2］研制了用于机器人手指力感知的微型五维力/力矩传感器；樊继壮［3］对于机器人足部力传感器的弹性体进行了研究；何小辉［4］研制了用于外科手术力觉信息采集的六维力/力矩传感器；梁桥康［5］研究了一种超薄六维力/力矩传感器的优化设计及其非线性解耦的问题。综上所列的力传感器在安装方式选择上，只能采用上下表面相连接的方式才能实现力和力矩传递，对于传感器有中空安装要求的场合，则不能满足要求，因此，笔者设计了一种新型的中空环形的三维力/力矩传感器，可以允许使用者在安装方式上有更多的选择。

1 传感器的结构设计

传感器性能与弹性体结构有着直接的联系，所以在整个传感器系统的设计中，弹性体的结构设计尤为重要，特别是多维力传感器。成功的弹性体设计往往使传感器具备各个方向的高灵敏度、维间耦合小以及良好的静动态特性。

将三维力/力矩传感器的弹性体设计为环形八字形孔（如图1所示），选用材料为硬质铝合金，牌号为2A12，杨氏模量为75 GPa，泊松比为0.33，整个弹性体一次性加工成型，外形为圆柱形结构，其上均匀分布有6个8字形孔，孔的上端为应变梁部分，12个应变片粘贴其上，组成3个惠斯顿桥路。弹性体内壁均布3根径向梁，相互成120°，下端均布3根轴向梁，与径向梁位置错开，相互之间也成120°。

▲图1 传感器外形结构

本文所设计的传感器具备测量多维力和力矩的功能，具体而言，可以检测沿传感器轴向方向垂直压力Fz，以及绕X轴和Y轴的力矩Mx、My，传感器结构设计目标应满足轻便、小巧并具有较高精度的要求，其设计指标为：Fz方向量程为5 N，Mx和My量程为0.3 N·m，测量精度不低于2%，分辨率不低于0.5%。

2 传感器弹性体的优化设计

为了提高传感器的动静态性能，对弹性体进行结构优化。传感器弹性体的结构尺寸如图2所示，其中，弹性体的高度B预先确定，优化设计的变量选择为：圆孔直径D、两圆孔的中心距S、弹性体厚度H以及单片八字形孔结构的长度L。确定这4个变量与弹性体性能的关系，就需要在ANSYS中进行多次的试验计算。为了能够在大量尺寸试验方案中挑选出少数几组试验方案，然后在这几个试验方案中挑选出最优方案，同时能够给出进一步的分析数据，本文采用正交试验法，最大限度减少计算量，较全面分析了4个主要结构变量对弹性体性能的影响，并对其结构进行优化。

选定D、S、H和L为试验的4个因素，先对每个因素分别选取4个水平值，其取值见表1，水平值的选取充分考虑了弹性体的结构和尺寸空间。

▲图2 弹性体结构尺寸

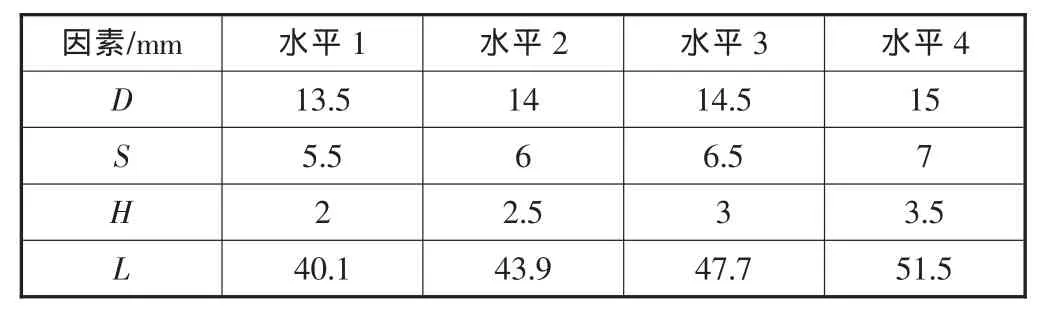
表1 正交试验水平值表

选定因素和相应的水平值后，再确定选用正交试验表。由表1知，这是一个4因素4水平的试验，应选用L1645型正交表。把4个因素依次放在表的第1列，各因素分别对应有4个水平，根据表1得到具体的试验方案见表2。在所有16次试验中，不同因素的各个不同水平出现了相同的次数，即水平和因素搭配都均匀，能全面代表256次试验，可以较全面反映各因素各水平对指标的影响情况。

根据正交表所设计的各变量的搭配方案，在SolidWorks软件中，分别构建相应的模型并导入到有限元分析软件ANSYS中，计算所对应的最大灵敏度的值，设定输入作用力和力矩，其中：Fz=5 N，Mx=0.3 N·m，My=0.3 N·m。

由表2的分析结果来分析各因素对于弹性体性能的影响。采用极差分析法，分析确定各因素对弹性体性能影响的主次关系。极差指的是各列中各水平对应的试验指标平均值的最大值与最小值之差，由此可分别得到三个方向作用力与弹性体灵敏度的关系。仅以Fz为例进行说明，见表 3，表中 Sumi（i=1,2,3,4）代表在某一因素下水平“i”所对应的试验指标的数值之和；Avei（i=1,2,3,4）代表在某一因素下，水平“i”所对应的试验指标的平均值；M代表在某一因素下，各水平对应的试验指标平均值中最大值与最小值之差。

由表3的M值可得出各因素对于弹性体在Fz方向灵敏度影响由强到弱的因素，依次为圆孔直径＞弹性体壁厚＞圆孔中心距＞弹性体长度，并且圆孔直径的改变将会剧烈地改变弹性体的灵敏度，采用此方法,对于Mx和My方向的灵敏度进行分析，也可以得到相类似的结果。

综上所述，在任意方向施加作用力，各因素对于性能影响的排序都是相同的，因此，这对于优化弹性体的结构提供了极大的方便，其中圆孔直径是最重要的影响因素。

3 测量原理

传感器应变片采用金属电阻应变式，其原理是一种利用金属电阻应变片将应变转换成电阻变化的传感器，具有结构简单、性能可靠和灵敏度高等优点。

当外力作用于传感器的连接件时，通过传感器上表面应变梁的变形，使传感器处理信号发生相应的变化，根据应变梁的变形方式，可将应变片所受应力分为压力和拉力。图3为传感器在受到Fz、Mx和My时传感器的弯曲变形状况，显然，传感器受力Fz、力矩Mx或My作用时，应变梁的正面产生了弯曲变形，因此，可以将应变片粘贴位置确定在应变梁的上端面，接下来的工作是确定应变片的粘贴位置。

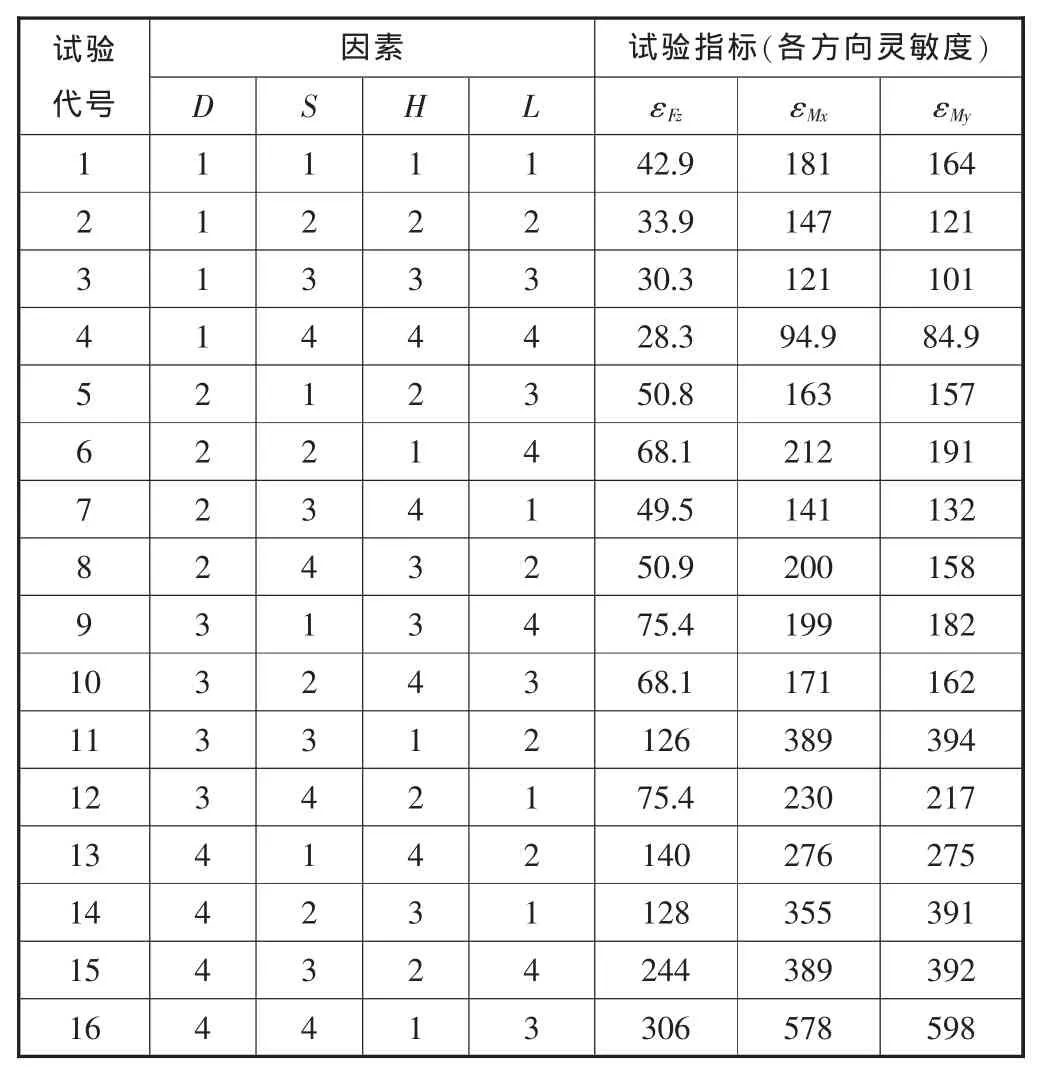
表2 正交表与计算分析结果

表3 Fz方向弹性体灵敏度的极差分析

根据优化后的分析计算，确定弹性体的最终尺寸，并在SolidWorks软件中构建弹性体的最终优化模型。在不影响弹性体精度的前提下，适当简化模型，并将简化后的模型以X_T文件形式导入到有限元分析软件ANSYS中。

选用3维20节点的Solid95作为单元类型，此单元能够容许不规则形状，并且不会降低精确性，同时，其偏移形状的兼容性好，具有塑性、应力刚度、大变形以及大应变等能力。因此，非常适合本传感器的有限元分析，因为弹性体的结构较为复杂，选用智能网格划分弹性体模型，其有限元模型如图4所示。

▲图3 传感器在外力作用下的变形情况

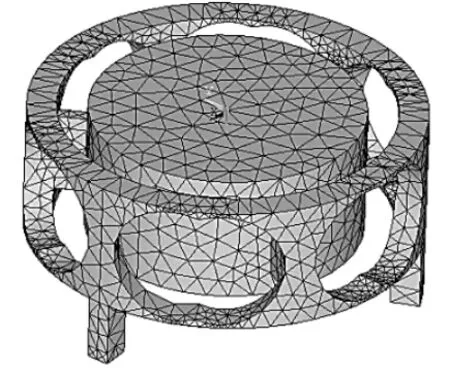
▲图4 弹性体的有限元模型

经过中间分析计算，可在后处理中得到Fz=5 N力作用下弹性体的应变云图和应变梁的应力曲线，分别如图5和图6所示。

传感器在Mx=0.3 N·m力矩作用下，弹性体的应变云图和应变梁的应力曲线分别如图7和图8所示。

传感器在My=0.3 N·m力矩作用下，弹性体的应变云图和应变梁的应力曲线分别如图9和图10所示。

对比图 6、图 8、图 10中的3条应力曲线，可以发现弹性体应变梁的最大形变位置是固定的，曲线的12个峰值刚好处于八字孔最上端所对应应变梁的相应位置。因此，可以选择这12个峰值点作为12个应变片的粘贴位置（均匀分布）。

图11确定了坐标系以及应变片的粘贴位置，选用电阻应变计的方式测量弹性体应力的大小，考虑将12个电阻应变片组成3个测量电桥。为将应变片所受作用力的微小变化测量出来，并有效提高电压灵敏度，考虑测量电路采用直流电桥的工作方式，其电路如图12所示。

当外力作用于传感器时，引起弹性体的变形，使贴在弹性体最大应变处的应变片发生相应的变形，改变其自身的阻值。通过应变片在电桥中的阻值变化，使桥路输出电压发生变化，根据此变化获得相应的信号，可以计算出对应的作用力/力矩。根据弹性体的结构特点和应变片的粘贴位置，得出应变片与力/力矩的变换关系：

▲图6 Fz=5 N，应变梁的应力曲线

▲图5 Fz=5 N，弹性体的应力云图

▲图7 Mx=0.3 N·m,弹性体的应力云图

▲图8 Mx=0.3 N·m，应变梁的应力曲线

▲图1 0 My=0.3 N·m，应变梁的应力曲线

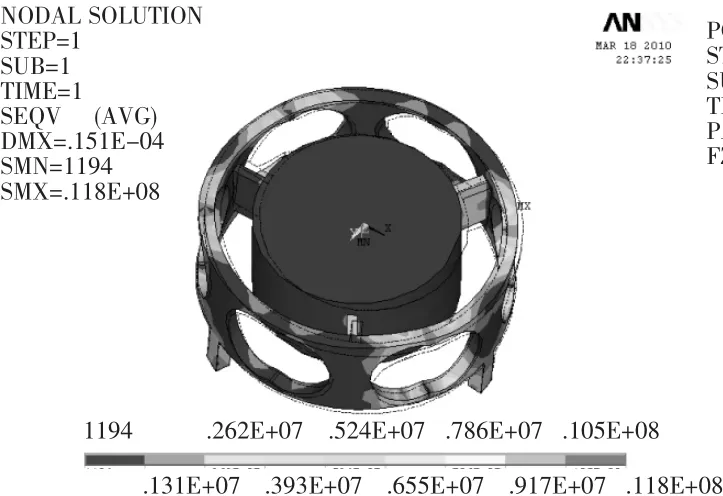
▲图9 My=0.3 N·m，弹性体的应力云图

式中：k 为应变片的灵敏度；εn（n=1，2，...，12）为第 n 片应变片在各力（力矩）作用下产生的应变；α为应变片2与X轴的夹角。

▲图1 1 应变片粘贴位置及坐标系设置

▲图1 2 测量电桥

▲图1 3 传感器样机

▲图1 4 数据采集系统原理框图

根据上述设计所制造的传感器样机如图13所示。

4 数据采集系统

所设计的传感器上共采用了12片应变片，组成了三组电桥，输出三路模拟信号，所以需要设计数据采集系统完成对传感器输出信息的采集。传感器数据采集系统的示意图如图14所示，主要由两部分构成：数字电路由微控制器与上位机接口通信电路组成，微控制器采用ADuC812，该微处理器内置8路12位A/D转换；模拟电路完成对传感器供电，对传感器信号进行放大、滤波等预处理。传感器的供电电源采用电压基准芯片，采用AD620对传感器信号进行差动放大处理。