基于Matlab的古塔变形分析

王雪萍， 杨庆生

（乌鲁木齐职业大学 基础教育部，新疆 乌鲁木齐 830002）

0 引 言

古代建筑物中的古塔造型在我国许多地区随处可见，一个时期一个地方的古塔建造体现一定的历史文化背景；一些古塔历经几个朝代，任凭风吹雨打，巍然矗立至今，体现着我国古代建筑设计师和建造师的聪明智慧。研究古塔的结构，分析古塔的变形对保护我国古建筑，研究我国历史文化和建筑设计有着重要的价值和意义。

本问题是2013年全国大学生数学建模竞赛乙组C题［1］，内容是：由于长时间承受自重、气温、风力等各种作用，偶然还要受地震、飓风的影响，古塔会产生各种变形，诸如倾斜、弯曲、扭曲等。为保护古塔，文物部门需适时对古塔进行观测，了解各种变形量，以制定必要的保护措施。某古塔已有上千年历史，是我国重点保护文物。管理部门委托测绘公司先后于1986年7月、1996年8月、2009年3月和2011年3月对该塔进行了4次观测。试给出确定古塔各层中心位置的通用方法，古塔各层的中心坐标；分析该塔倾斜、弯曲、扭曲等变形情况；分析该塔的变形趋势。

1 古塔形状的确定和缺失数据的预测

1.1 对所给的古塔测量数据进行分析，确定古塔形状

假设每次测量观测方法相同，用同一仪器和设备，在基本相同的环境和条件下观测，所测量的数据都是真实、精确、可靠的。对附件中提供的某古塔1986年、1996年、2009年、2011年4次每层8个观测点的测量数据进行观察，发现该古塔共有13层，每层有8个观测点，塔尖有4个观测点，且只有1986年和1996年的观测数据，2009年和2011年数据缺失，故不考虑塔尖的变形。对给与的观测数据的横坐标和纵坐标应用excel绘图功能做散点图，发现每层8个测量点近似呈八边形分布，1986年和1996年的每层8个测量点观测顺序和2009年、2011年测量点观测顺序不一致，如图1和图2所示。

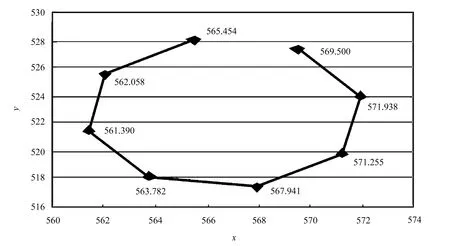
图1 1986年第1层8个观测点坐标平面图

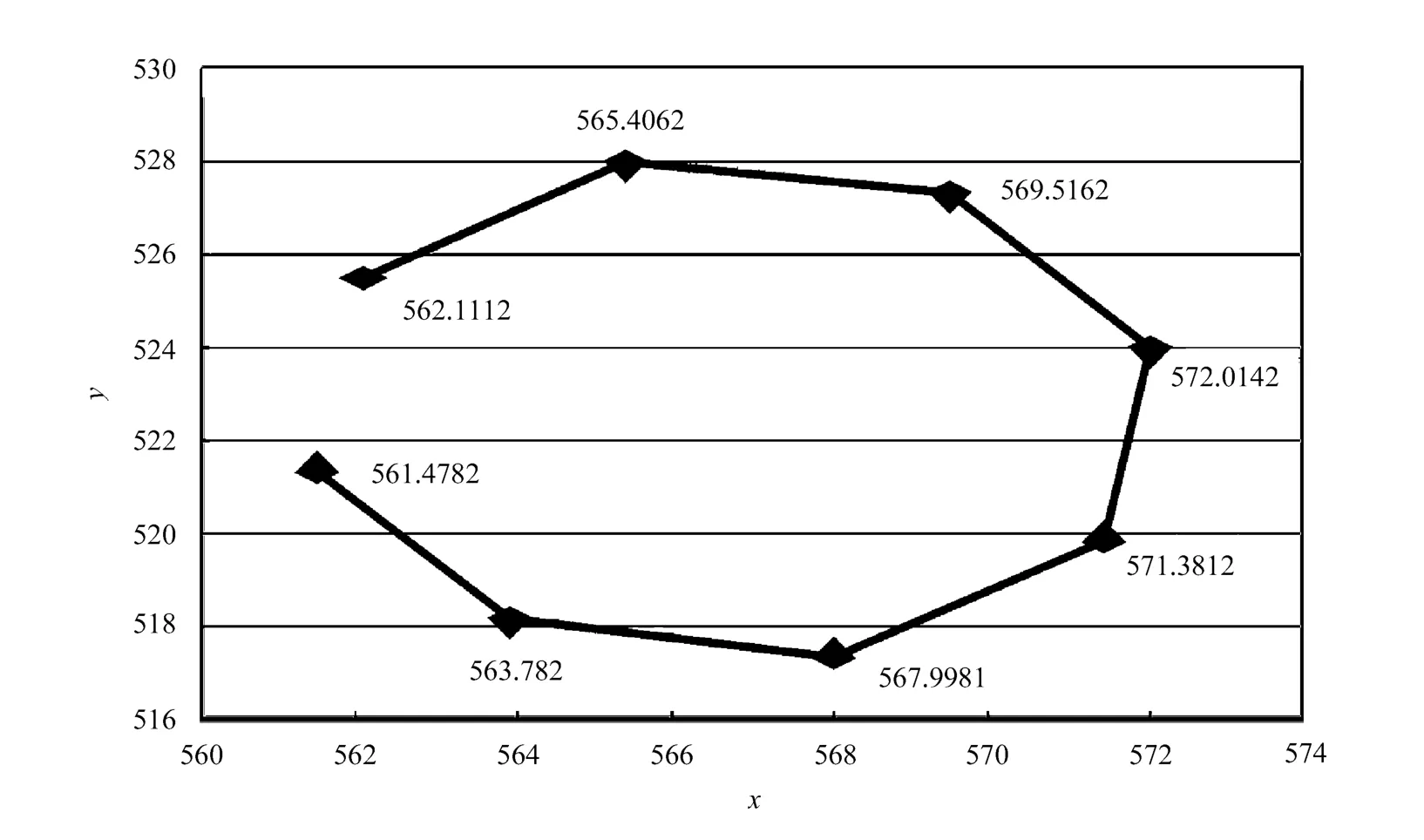
图2 2009年第1层8个观测点坐标平面图

为了方便分析，我们从横坐标值最小的测量点开始编号，即按照2009年和2011年的测量点顺序调整1986年和1996年每层8个观测点的顺序，即1986年和1996年各层的观测点顺序由12345678改为78123456。即古塔每层近似呈八边形，且上小下大。1986年古塔空间立体图如图3所示。

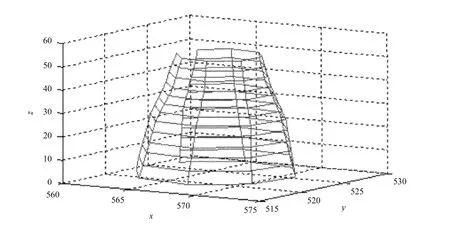
图3 1986年古塔空间立体图

1.2 对1986年和1996年第13层观测点3的缺失数据预测

由于所提供的1986年和1996年第13层观测点3的坐标数据缺失，为了便于分析，需要对缺失的数据进行预测。1986年、1996年、2009年、2011年每层观测点3的空间坐标用Matlab7.0绘出的图形如图4所示。

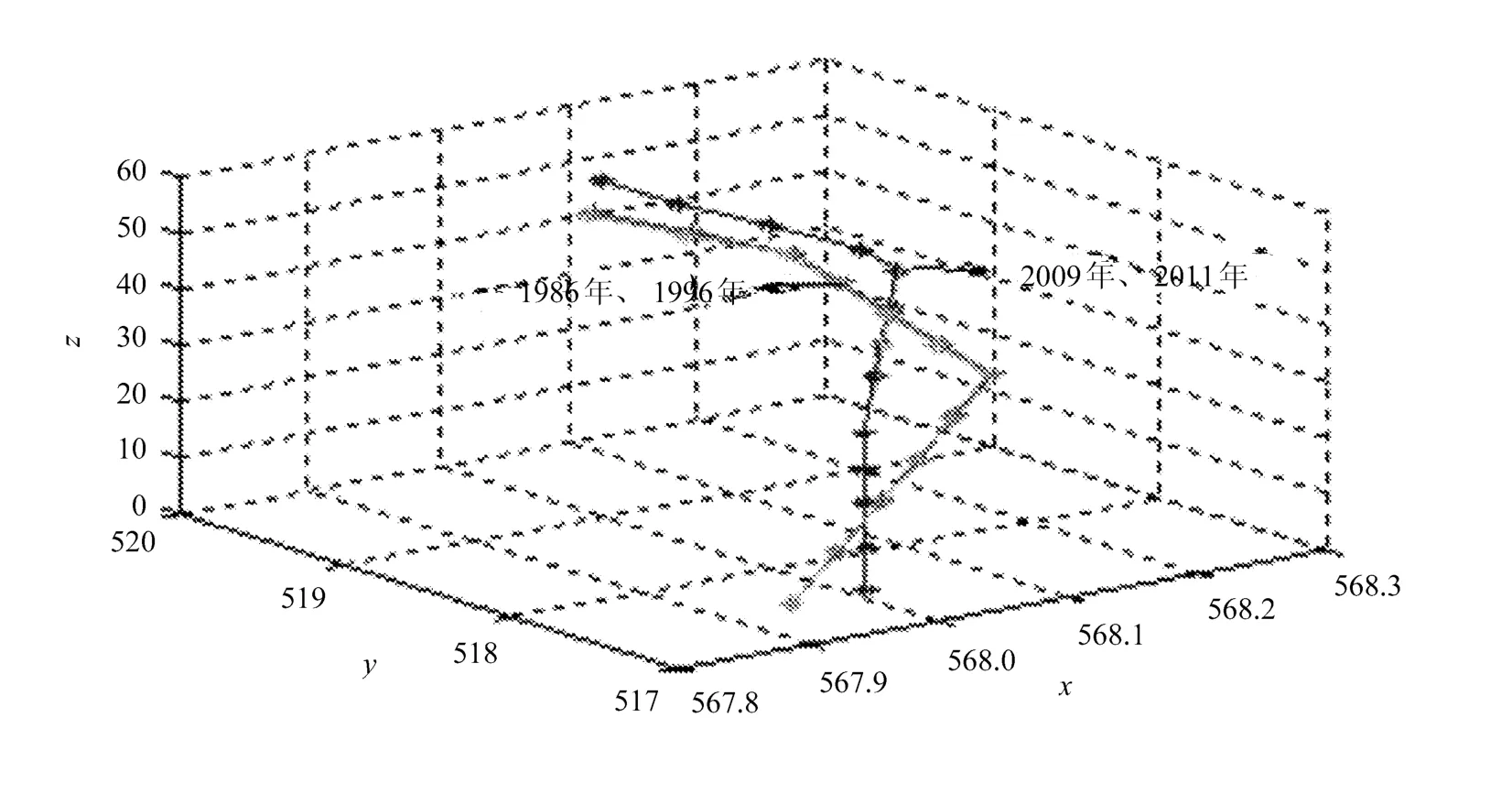
图4 1986年、1996年、2009年、2011年各层第3个观测点空间图形

可以从图形直观看出，古塔在第3个观测点上，1986年和1996年、2009年和2011年测量的数据空间图形几乎一致，变化不大，但是，1996年到2009年这14年间古塔在第3个观测点处变化比较大，在10层到13层上这4次变化趋势是一致的，呈线性趋势。

用xi，yi表示第i层的横坐标和纵坐标，Δxi＝xi－xi－1，Δyi＝yi－yi－1分别表示相邻两层横坐标和纵坐标的改变量［2］，则

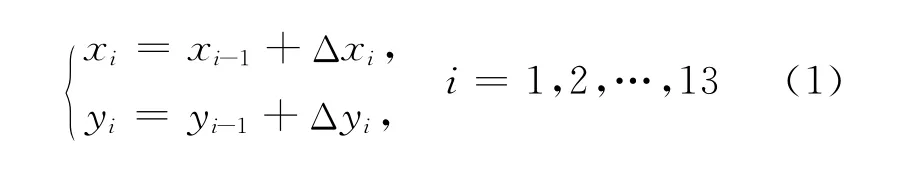
对1986年和1996年第13层第3个观测点的缺失的横坐标和纵坐标用式（1）预测，结果见表1。

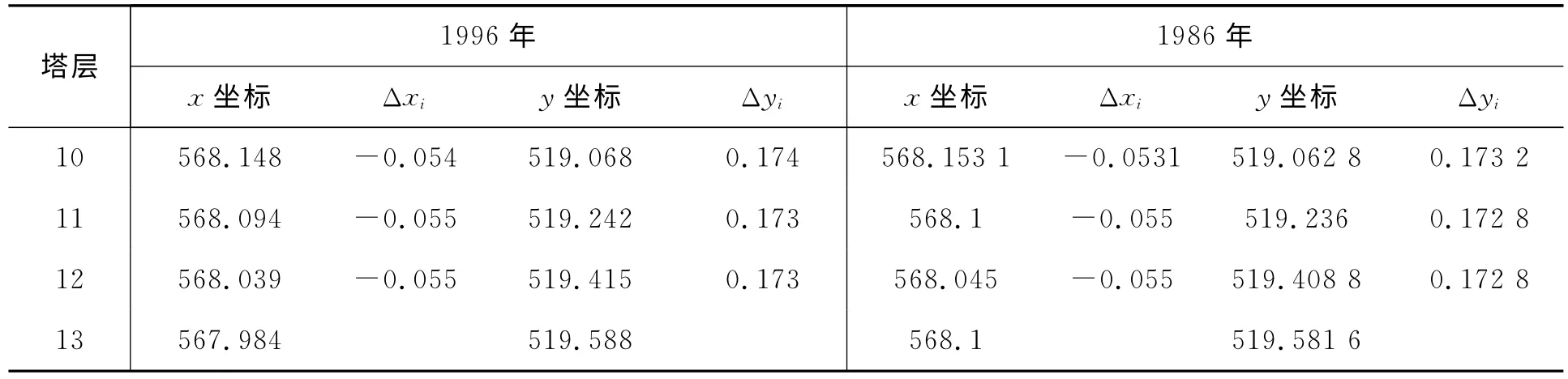
表1 1986年、1996年第13层观测点3缺失数据预测 m

由表1可以看出，各层的绝对改变量Δxi和Δyi很小，相差1mm，这样可以近似用第12层的改变量来推测第13层的坐标。

1986年：

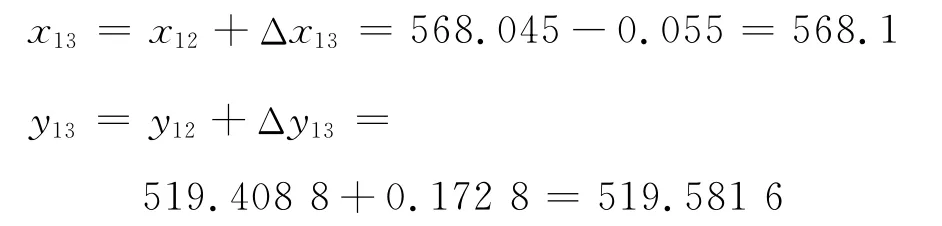
1996年：对于观测点3的z3值，如果把各层看做在同一平面上的话，运用均值法，即用该塔第13层其余7个观测点的竖坐标的平均值来作为z3的预测值，则

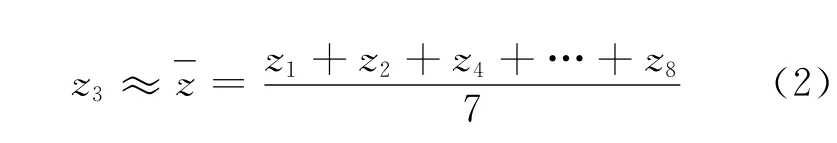
以此类推：得出1986年第13层测量点3坐标（567.984，519.588，52.834）、1996年第13层测量点3坐标（568.1，519.581 6，52.83）。

另外一种方法可以应用Matlab软件做线性拟合。

1986年第13层观测点3的x坐标预测，从第10层开始取x坐标值，Matlab命令：

＞＞tr＝［10 11 12；568.148 568.094 568.039］；

＞＞t＝tr（1，：）＇；

＞＞x＝tr（2，：）＇；

＞＞p＝polyfit（t，x，1）

则横坐标x的拟合函数x＝568.693－0.054 5t，把t＝13代入，x＝567.984 67。

纵坐标y拟合函数y＝517.333＋0.173 5t，把t＝13代入，y＝519.588 667。

两种方法预测的x和y坐标误差分别是0.67mm和0.667mm，非常小，故这两种方法用来预测缺失数据都可行。

2 古塔变形的分析

2.1 各层中心坐标的确定

古塔建造初期应该是一上小下大的正八边形空间立体，除了第1层外，其它各层是一个截面为八边形的正棱台，经过上千年，古塔发生了变形，不再是一个规则的正八边形，由于所提供的数据是每层8个点的测量坐标，为了简化问题，方便问题的解决，我们把每层看做一个八边形正棱柱。正八边形内接于圆，内接圆的圆心即可作为所在层的中心，可以用正八边形拟合圆的方程，则圆心坐标是各层中心的横坐标和纵坐标。第k层拟合的圆方程：

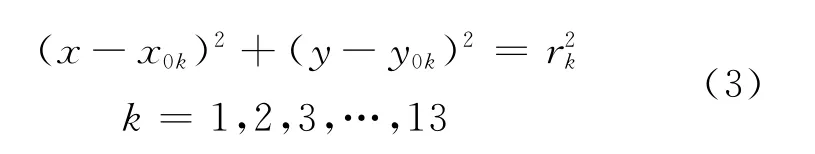
根据所给各观测点的横坐标和纵坐标用Matlab软件拟合圆的方程。1986年第1层的中心横坐标和纵坐标的Matlab命令［3－4］：

则可得拟合圆心坐标（566.665，522.709）。假设测量点位于各层的顶部，则各层中心应该位于相邻两层的中间位置，第1层中心的竖坐标取层高的平均值的二分之一，第k层中心竖坐标记为zk0，其中

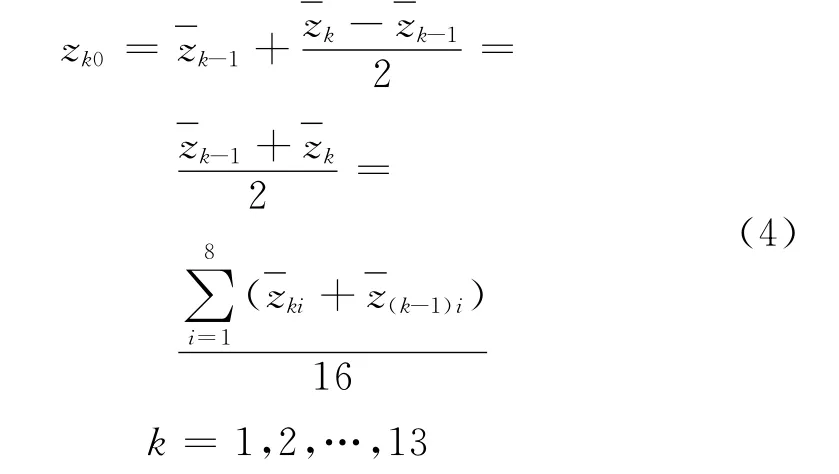
则可得1986年第1层的中心坐标为（566.665，522.709，0.894），同 理，可 以 计 算 出1986年第2层的中心坐标（566.723，522.671，4.554）。

另外，计算各层中心的简单方法可以用各层8个测量点的横坐标和纵坐标的平均值来近似表示各层的中心坐标，即

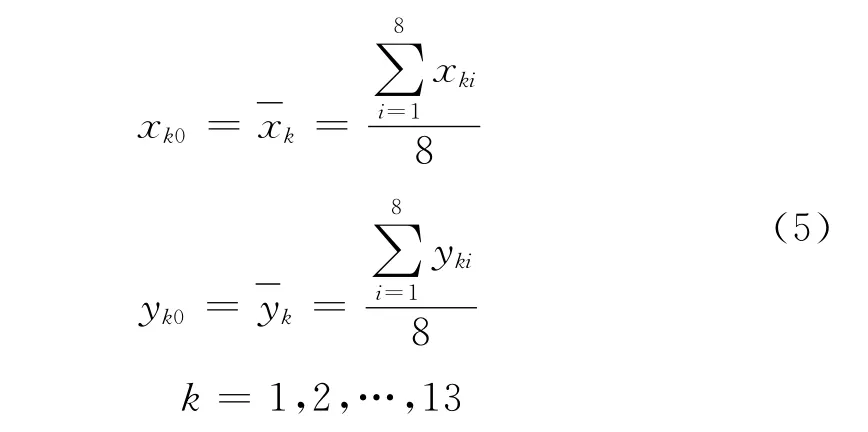
则可得1986年第1层的中心坐标为（566.665，522.711，0.894），同理，可计算出1986年第2层中心坐标（566.720，522.668，4.554），两种方法计算的中心坐标偏差均小于0.005m，因此两种方法计算中心坐标都是可行的。

2.2 古塔的倾斜、弯曲、扭曲分析

2.2.1 古塔的倾斜分析

如果古塔没有倾斜，各层的中心坐标应该在古塔中心轴上，即其投影在xoy平面上的同一点处，根据建筑施工误差标准，轴线位置偏移＜10mm是允许的［5－8］。由1986年各层的中心坐标可以看出，古塔的中心坐标不在同一点处，做1986年各层中心在xoy面的投影坐标图，如图5所示。

中心坐标在x轴上的极差0.542m，在y轴上的极差0.348m，且横坐标随着层数的增加递增，纵坐标随着层数的增加递减，即向x轴正向倾斜。记第1层与第13层中心的投影距离为l1，13，塔身与xoy平面的夹角α，则

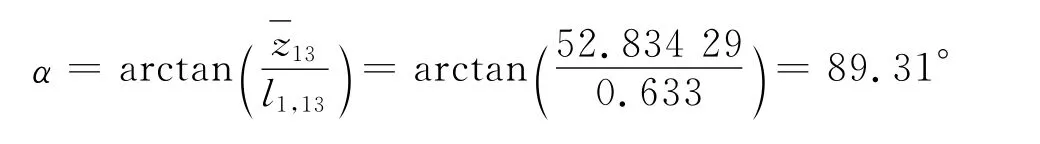
即1986年塔的倾斜角为89.31°。同理，可计算出1996年塔的倾斜角为89.303°；2009年塔的倾斜角为89.251°；2011年塔的倾斜角为89.246°。可以看出，1986年和1996年塔的倾斜变化不大，1996年到2009年间塔的倾斜变化较大，2009年和2011年间塔的倾斜变化不大。

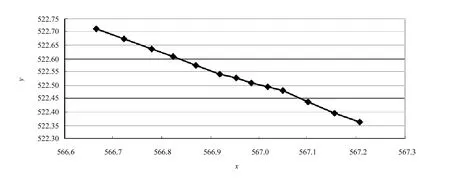
图5 1986年古塔各层中心坐标在xoy平面的投影

对各层8个观测点的高计算层高差、平均层高、层高均方差，见表2。

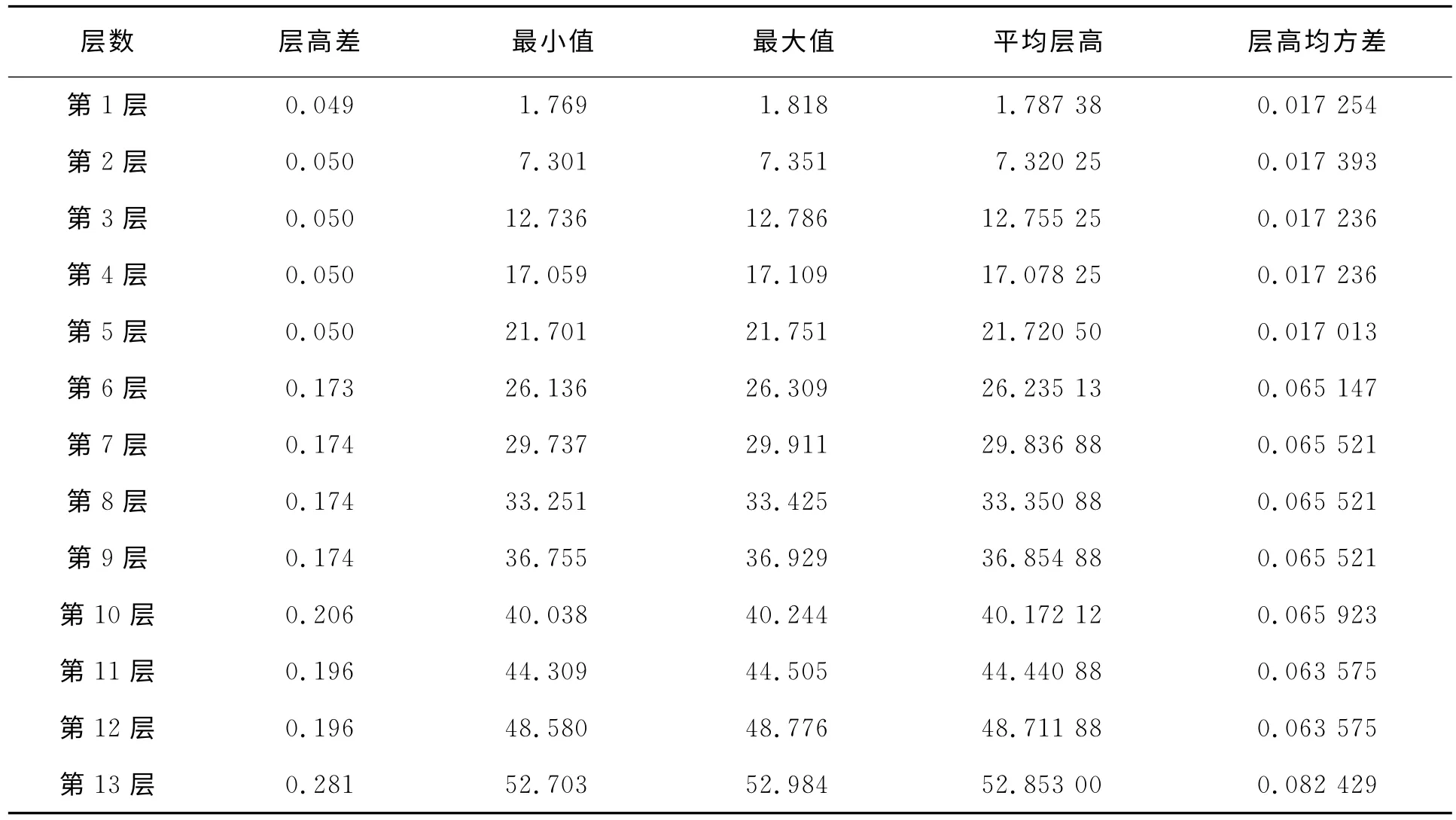
表2 1986年各层8个观测点层高数据统计

对于1986年的古塔各层8个观测点的z坐标进行分析，得出各层高的变化趋势，第1层到第5层极差较小，倾斜程度不大，第6层到第10层极差较大，倾斜较大，第11层和第12层次之，第13层倾斜最大。

其它3年的分析方法相同。

2.2.2 古塔的弯曲与扭曲分析古塔建造初期应该是一个正八棱台，每层8个观测点在xoy平面的投影应该是均匀分布的直线，如果弯曲，则在xoy平面的投影不再是均匀分布的直线，如果没有发生扭曲，则在xoy平面各层的观测点的投影的距离就是非均匀分布。如果发生扭曲，则投影就不在同一条直线上。1986年古塔13层8个观测点空间曲线和每层8个观测点在xoy平面的投影分别如图6和图7所示。

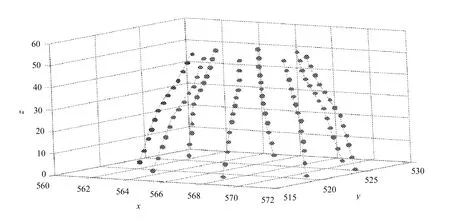
图6 1986年古塔各层8个观测点空间线图

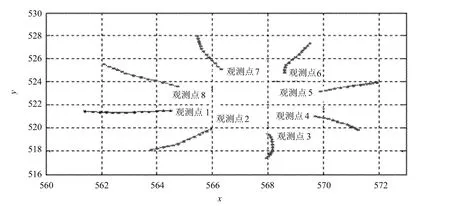
图7 1986年古塔各层8个观测点在xoy平面投影点

从1986年各层8个点的空间线图可以直观看出，1～6层变化不大，从第7层开始发生弯曲，第7层正好处于该塔的中心位置，可能受重力的作用开始发生弯曲。

1986年每层8个点在xoy平面上的投影不在一条直线上，可以看出发生了扭曲，观测点7，8从第7层开始向x轴正向发生扭曲，观测点6到第10层扭曲较大，观测点5扭曲不明显，观测点4和观测点3、观测点2都从第7层开始扭曲，其中观测点3扭曲较严重，观测点1扭曲不明显。

2.2.3 古塔变形趋势分析

根据测量的坐标数据，用Matlab7.0做出1986年、1996年、2009年、2011年观测点1的空间曲线如图8所示。

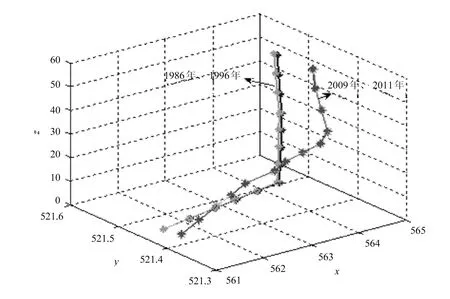
图8 1986年、1996年、2009年、2011年观测点1的空间曲线

从图形观察可以看出，1986年和1996年这两次测量，古塔的变形不大，2009年和2011年两次测量古塔变形也不大，但在1996年和2009年期间，也许发生了地震、飓风等原因，古塔发生了很大的变形。从1986年和1996年这两次测量可以看出，从第7层开始发生了弯曲，其它形变不明显，而2009年，从第1层开始到第5层观测点1发生了位移和整体倾斜，向着y轴正向倾斜，从第6层开始到7，8，9层发生了弯曲和扭曲，从第10层开始再一次发生了弯曲和扭曲现象，之后的2011年测量，几乎变化不大。结合图4的第3个观测点的空间图形，可以看出变形情况基本一致。

3 结 语

应用Matlab7.0对某古塔4次测量数据进行分析，给出了每层中心坐标的2种算法及塔与xoy平面的倾斜角，结合观测点在平面的投影和空间曲线图，得出1986年和1996年两次测量，古塔变化不大，1996年到2009年期间，古塔发生了严重的变形，2011年相对于2009年古塔的变化不大，说明1996年至2009年期间有可能发生了地震、飓风等自然灾害。在没有地震、飓风等发生的情况下，由于受重力等影响，古塔易发生倾斜，在其高度的1／2处易发生较明显的弯曲，在2／3处也易发生轻微弯曲；由于受风力和风向影响，古塔在其高度1／2之上处容易发生扭曲，高度的1／2处之下一般比较稳固，对于文物保护部门来说，古塔高度的1／2处及以上楼层要多加关注，及时采取保护措施。

［1］ 全国大学生数学建模竞赛网.2013年高教社杯全国大学生数学建模竞赛赛题［EB／OL］.［2014－12－22］.http：／／www.mcm.edu.cn／.

［2］ 李丽，王振领.MATLAB工程计算及应用［M］.北京：人民邮电出版社，2003.

［3］ 同济大学数学教研室.高等数学［M］.6版.北京：高等教育出版社，2007.

［4］ 苏金明，阮沈永.MATLAB实用教程［M］.北京：电子工业出版社，2005.

［5］ 卜璞，向亭译.用整体方差分析法对变形监测数据进行处理［J］.科学技术与工程，2012，12（2）：407－409.

［6］ 丁宁，孙英俊.高层建筑物变形监测数据处理与分析［J］.测绘科学，2011，36（5）：93－95.

［7］ 黄强.古塔变形检测的探讨［J］.测绘与空间地理信息，2013，36（6）：217－220.

［8］ 张方程，李晓天.同心圆亚像素中心定位方法［J］.长春工业大学学报：自然科学版，2014，35（5）：500－505.