P*-型非线性互补问题解的存在性

王秀玉，　李　琳

(长春工业大学 基础科学学院， 吉林 长春　130012)



P*-型非线性互补问题解的存在性

王秀玉，李琳

(长春工业大学 基础科学学院， 吉林 长春130012)

摘要：首先利用Poincare-Bohl定理给出择一性定理，然后用该定理证明非线性互补问题解的存在性，并获得互补问题有解的充分条件。

关键词：互补问题； 择一性定理；P-型映射；P*-型映射

0引言

互补问题首先由著名运筹学家、数学规划的创始人G.B.Dantzig教授和他的学生R.W.Cottle于1963年提出，由于互补问题在数学规划、对策论及经济学等领域有广泛应用[1-2]，受到极大关注。判定互补问题是否有解及获得互补问题有解的充分或必要条件是研究互补问题的重要问题之一。求解互补问题的方法之一为构造一个择一性定理，即对连续函数所对应的互补问题构造适当的例外簇，互补问题或者存在例外簇，或者有解，然后给出互补问题没有例外簇的条件，进而得到互补问题有解。文献[3]比较全面地论述了互补问题的基础理论和求解的几种重要方法；文献[4]给出了一种例外簇的具体形式，文献[5]利用文献[4]的择一性定理，获得了一些非单调互补问题存在解的条件;王秀玉[6]等讨论了水平互补问题。其它的互补问题是否存在解，利用文献[4]的择一性定理能否判定，还未有结论。

文中讨论如下非线性互补问题(NCP(f)):求x≥0，使得y=f(x)≥0，且xTy=0，其中f:Rn→Rn为连续映射。文中利用NCP函数构造与文献[4]类似的例外族，并证明了P*-型映射所对应的互补问题的可解性。

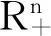
1择一性定理

首先介绍在拓扑学中广泛运用的两个基本结论。

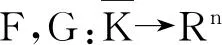
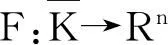
下面是文中给出的例外簇的定义。

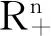
则称序列{x(r)}为NCP(f)的例外簇。

利用极小函数及Poincare-Bohl定理,首先证明一个择一性定理。

定理1设f:Rn→Rn是一连续映射，则互补问题(NCP)或者有解或者存在例外簇。

证明因互补问题(NCP)等价于

若式(1)无解，记

考虑同伦方程：

则对∀r>0,∃tr∈[0,1]及存在x(r)∈∂Dr，使得

否则，∃r*>0，对∀x∈∂Dr*，∀t∈[0,1]，有

因此

由引理1知

再由引理2知，φ(x)=0有解，与题设矛盾，从而式(3)成立，且式(3)中的tr∈(0,1)。

若tr=0，则有φ(x(r))=0，与证明开始假设互补问题无解矛盾。

若tr=1，则有x(r)=0，这与x(r)∈∂Dr矛盾。

因为x(r)∈∂Dr，故有

式(3)的分量形式为：

整理式(5)得：

式(6)两边平方得：

化简式(7)得：

即

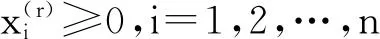
由式(9)得：

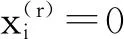
由式(4) ‖x(r)‖→+∞，(r→+∞)，从而{x(r)}是互补问题NCP(f)的例外簇。

由定理1立即可得

推论1设f:Rn→Rn是连续函数，且互补问题NCP(f)无例外簇，则互补问题NCP(f)有解。

2互补问题的解的存在性

利用定理1证明一些互补问题有解。

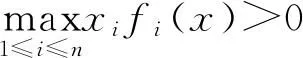
定理2若f为连续的P-型映射，则互补问题NCP(f)有解。

证明只需证明互补问题无例外簇即可。

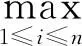
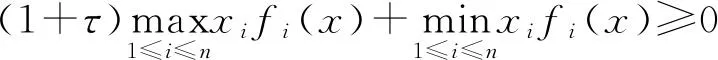
定理3若f为连续的P*-型映射，则互补问题NCP(f)有解。

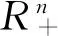
上式与P*-型映射矛盾，因此，互补问题NCP(f)有解。

下面给出P*-型映射的推广。

定义4设映射f:Rn→Rn，若∃τ≥0，α≥0，β∈(0,1)对∀x∈Rn，有

则称f为P(τ,α,β)-型映射。

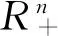
定理4若f为P(τ,α,β)-型映射，且互补问题没有无穷远解，则互补问题NCP(f)有解。

证明由定理1知只需证明互补问题无例外簇即可。

即

整理得

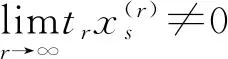
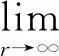
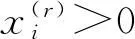
将式(12)代入上式得

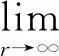
参考文献：

[1]Dantzig G B, Cottle R W. Positive (semi-definite) matrices and mathematical programming [D]: [Ph D Thesis]. Colifornia: University of Berkeley,1963.

[2]Pang J S, Kaneko I, Hallman W P. On the solution of some (parametric) linear complementarity problems with application to portfolio selection[J]. Math.Programming,1979,16:325-347.

[3]韩继业,修乃华,戚厚铎.非线性互补理论与算法[M].上海:上海科学技术出版社,2006.

[4]Isac G, Bulavski V, Kalashnikov V. Exceptional families, Topological degree and complementarity problem[J]. Journal of Global Optimization,1997,10:207-225.

[5]Zhao Y B, Isac G. Quasi-P*-maps,P(τ,α,β) maps, exceptional family of element, and complementarity problems[J]. Journal Optimization Theory and Applications,2000,105(1):213-231.

[6]王秀玉，申海明，李琳.水平线性互补问题中常用矩阵对及其性质[J].长春工业大学学报：自然科学版，2013，34(2)：121-126.

[7]Ya-Ping, Nan-Jing Huang, Yeol Je Cho. Some characteristic quantities associated with homogeneousP-Type andM-Type functions[J]. Journal of Inequalities and Applications,2007,146(84):1-10.

[8]王秀玉,姜兴武,刘庆怀.求解互补问题的新同伦算法[J].吉林大学学报:理学版,2012,50(3):494-498.

Existence of the solution ofP*- type nonlinear complementarity problem

WANG Xiu-yu,LI Lin

(School of Basic Science, Changchun University of Technology, Changchun 130012， China)

Abstract：An alternative theorem is proposed by using Poincare-Bohl theorem to prove the existence of the solution of some nonlinear complementarity problems and obtain the sufficient conditions this kinds of problem.

Key words：complementarity problem; alternative theorem;P- type mapping;P*- type mapping.

中图分类号：O 224

文献标志码：A

文章编号：1674-1374(2015)02-0121-04

DOI:10.15923/j.cnki.cn22-1382/t.2015.2.01

作者简介：王秀玉(1965-)，女，汉族，吉林长春人，长春工业大学教授,硕士，主要从事最优化的理论与算法研究,E-mail:wangxiuyu.000@163.com.

基金项目：国家自然科学基金资助项目(10071020)； 吉林省自然科学基金资助项目(201215128,20101597)

收稿日期：2014-10-20