客户时间窗变化的物流配送干扰管理模型
——基于行为的视角
2015-06-12丁秋雷
丁秋雷
(东北财经大学工商管理学院,辽宁 大连 116025 )
客户时间窗变化的物流配送干扰管理模型
——基于行为的视角
丁秋雷
(东北财经大学工商管理学院,辽宁 大连 116025 )
针对客户时间窗变化而导致的物流配送难以顺利实施这一难题,运用干扰管理思想,以提高物流配送干扰管理决策过程的科学性为目标,结合行为科学中对人的行为感知的研究方法与运筹学中定量的研究手段,分析客户时间窗变化这类干扰事件对客户、物流配送运营商和配送业务员等受扰主体的影响,研究基于行为的扰动度量方法, 构建客户时间窗变化的字典序多目标干扰管理模型,并给出快速高效的求解方法。实例结果表明:本文方法比已有的全局重调度方法和局部重调度方法更实用——能够均衡各方的利益,获得扰动最小的调整方案。
管理工程;物流配送;干扰管理;前景理论;多目标优化
1 引言
随着社会的发展,人们在生活、工作上的节奏越来越快,时间不确定性也随之越来越高,使得在物流配送过程中,经常有客户临时要求变更配送时间[1]。然而,随着电子商务的普及,物流配送已呈现出送货点分散且点多面广、送货批量小且成本高等特点,由于物流企业运力有限,因此难以适应客户变更配送时间的要求,这就使正在执行的配送方案变得不可行,目前在大家电、贵重物品、重要文件等需要客户亲自签收的快件配送上,已经产生了一系列问题。
因此,如何科学地对配送方案进行调整尤为重要!由于物流配送系统是一个典型的“人—机”系统,除了考虑降低成本损失之外,“人”的参与也必须受到重视。而人在面对扰动时做出的反应是不同的,因此当某一个客户的时间窗发生变化后,需要调整剩余客户的配送顺序,这样势必导致连锁反应,造成整个系统的混乱。此时就需要考虑扰动对整个物流配送系统的影响,生成使系统扰动最小的调整方案。在这种情况下,物流配送问题变得更加复杂,现有的方法和理论体系将难以胜任相关的研究工作。因此,如何有效地处理干扰事件,已成为影响现代物流产业发展的关键!
干扰管理[2]正是一种致力于实时处理这类问题的方法论,它需要针对各种实际问题和扰动的性质,建立相应的优化模型和有效的求解算法,通过对初始方案进行局部优化调整,实时生成使系统扰动最小的调整方案。这个调整方案不是针对扰动发生后的状态完全彻底地重新进行建模和优化,而是以此状态为基础,通过对初始方案进行局部优化调整,快速生成使系统扰动最小的调整方案。
干扰管理自提出以来,已成功应用到航空[3]、机器调度[4]、供应链[5]、项目管理[6]等多个领域。在客户时间窗变化的物流配送干扰管理研究上,Wang 等[7]针对中国邮路问题,采用模糊理论对客户的时间窗进行表示,构建了服务水平最大化和任务完成时间最小化的数学模型;王明春等[8]针对需求变动和时间窗变化,构造了扰动模型对物流配送系统进行恢复;钟石泉等[9]针对客户时间窗和发货量的变化,通过设计虚拟车场等方法实现车辆的紧急调度;王旭坪等[10]为解决由客户时间变化引发的物流配送干扰问题,提出相应的扰动恢复策略;Hadjar 等[11]针对客户时间窗变化问题,在考虑配送成本的情况下构建数学模型,并采用分支定界法进行求解;王征等[12]提出包含客户配送时间总偏离度、配送总成本、路径偏差量、最长行驶时间违反总量4 个因素的扰动程度度量方法,以系统整体扰动最小化为目标,建立问题的目标规划数学模型;王旭坪等[13]采用时间窗模糊化处理方法定义客户满意度函数,根据干扰管理思想对车辆调度中组合性干扰事件进行分析,建立基于模糊时间窗的车辆调度组合干扰管理模型;杨文超等[1]以客户时间窗变化这类干扰事件发生时的问题状态为基础,提出了新车增派策略和多车协作策略,并在此基础上建立了问题扰动救援的启发式算法。以上学者虽然为解决客户时间窗变化的物流配送干扰问题开辟了新的思路,但是,由于物流配送系统是一个典型的“人— 机”系统,包括客户、物流配送运营商、配送业务员等多个主体,现有研究过分重视物力、财力的调整与优化,而忽略人的行为因素,从而导致寻得的最优解往往在实践中并不可行。因此,针对客户时间窗变化的物流配送干扰管理这一多目标的、主观与客观相结合的优化难题,如何在考虑人的行为因素的情况下,通过权衡各方利益,形成一个多方满意的调整方案,从而以尽量小的扰动,尽快恢复系统的正常运行,是目前该领域存在的主要难题。
本文针对上述难题,通过结合行为科学中对人的行为感知的研究方法与运筹学中定量的研究手段,提出基于前景理论的扰动度量方法,构建客户时间窗变化的物流配送干扰管理模型及其求解方法,以期为物流配送干扰管理的决策过程提供支持。
2 扰动的分析
干扰事件发生后,为了有效地生成使系统扰动最小的调整方案,需要对扰动造成的影响进行分析,从而确定目标函数。由于客户、物流配送运营商以及配送业务员是使物流配送过程能够顺利运行的行为主体,三者的利益是研究的关键。因此, 本文首先分析扰动对上述行为主体的影响,确定各主体考虑的首要目标,具体如下:
(1)客户:客户是物流配送过程的接收者。当某个客户的时间窗发生变化后,需要调整剩余客户的配送顺序,这样势必引起连锁反应,影响后续一系列剩余货物的配送,使得某些客户无法按时收到货物。因此,对于客户来说,能否按时收到货物, 是其考虑的首要目标。
(2)物流配送运营商:物流配送运营商是物流配送过程的主导者。扰动发生后,配送车辆的行车路线随之发生变化,此时必然影响配送成本。由于在整个物流配送过程中,配送成本是物流配送运营商关注的核心,因此,在生成调整方案时,应适当兼顾成本因素,尽可能节省配送成本。
(3)配送业务员:配送业务员是物流配送过程的执行者。当系统发生扰动后,初始配送方案将变得不可行。在新的调整方案下,势必需要更改行车路线,这就会影响配送业务员的工作情绪。如果新的行车路线与初始的行车路线具有较大偏差,将有可能导致配送业务员消极怠工。因此,调整方案与初始方案之间配送路线的偏差大小,是配送业务员考虑的首要目标。
本文通过分析上述三个行为主体面对扰动时所关注的目标,对三者的利益进行权衡,从而度量系统的扰动程度,以形成使系统扰动最小的调整方案。
3 基于前景理论的扰动度量方法
由第2 节可知,物流配送系统包含多个主体, 是一个典型的“人—机”系统,扰动必然会对人的行为产生影响。因此,现有在完全理性假设条件下的研究成果难以直接用于解决实际的物流配送干扰管理问题。
前景理论[14-15]是行为科学中具有重大影响的一种行为决策理论,它以人的有限理性为基础,能够更加真实的描述人在不确定条件下的决策行为。因此,本节以前景理论为基础,提出系统扰动的度量方法。
3.1 价值函数的表示
扰动发生后,由于各主体考虑的目标不同,因此,基于前景理论,对各个目标的价值函数进行表示,其中目标i的价值函数Vi(x) 可表示为:
(1)
其中:αi、βi、λi为参数。
函数的形状如图1 所示(Oi为目标i的参照点)。

图1 目标i 的价值函数
由图1 可知,人们在开始决策时,首先需要选择一个价值为0的参照点,进而才能判定结果到底是盈利还是亏损。由于人们在决策选择时只注意其差异,如果保持现状就等于没有选择,它本身的价值为0,因此,本文选择现状作为参照点。
3.2 不满意隶属函数的确定
由于各目标的主体是人,而人又是主观的,对扰动的感知是模糊的。因此,需要对各目标进行模糊化处理。
设xi的不满意隶属函数为μi(xi), 当μi(Ri) =1时,基于前景理论,此时人们面临的是亏损,表现出来的是风险追求,根据式(1)可知:
μi(Ri)=-Vi(-Ri+Oi)=-[-λi(-(-Ri+Oi))β i]=λi(Ri-Oi)βi
(2)
由μi(Ri) =1,可知Ri=Oi+(1/λi)1/βi。因此,μi(xi) 可分为以下三段来表示:
(1)当xi≥Ri时,μi(xi) =1 ;
(2)当Oi≤xi (3)当0≤xi 综上,xi的不满意隶属函数可表示为: (3) 函数形状如图2 蓝色曲线所示。因为Ri由βi和λi来决定,而对于不同主体,βi和λi是不同的, 因此Ri也是不同的。可采用实证研究的方法,通过对各主体进行问卷调查,以确定上述参数。 图2 xi的不满意隶属函数 3.3 扰动度量函数的构建 根据3.2 节,对各目标采用不满意的隶属度进行度量。目标i的不满意度越小,对主体i的扰动越小。因此,目标i的扰动度量函数为: di(xi)= minμi(xi)i=1,…,n (4) 本节首先建立初始方案的数学模型。当系统发生扰动后,在该模型的基础上,构建调整方案的干扰管理模型。 4.1 初始方案的数学模型 4.1.1 问题界定 本文对要研究的物流配送问题描述如下: (1)每辆车从配送中心出发,沿着一条路线把装载的货物配送到指定客户后,返回配送中心; (2)每辆车可以服务多个客户,但每个客户的货物只能由一辆车配送; (3)每辆车所载货物不能超过装载能力,为简化问题,假设所有车辆的装载能力相同; (4)每个客户都有其接受服务的时间窗,即客户对货物到达时间的要求是在某个时间段上。 要求合理安排车辆配送路线和行车时间,使得目标函数最优,即准时到达和成本最低。 4.1.2 参数及变量说明 n:客户总数量; V:客户点集合,V={v0,v1,…,vn},v0代表配送中心,其他代表客户点; K:车辆总数; Cij:车辆从vi到vj的配送成本; tij:车辆从vi到vj的行驶时间; qi:vi的需求量; Q:车辆的装载能力; [ETi,LTi]:vi的时间窗。其中,ETi是客户要求到货时间段的始点,LTi是客户要求到货时间段的终点; ti:车辆到达vi的时间; wi:车辆对vi的服务时间; 4.1.3 数学模型 根据以上描述,建立物流配送初始方案的数学模型如下: (5) (6) (7) (8) (9) (10) (11) (12) ETi≤ti+wi≤LTii=1,…,n (13) 上述模型中,式(5)为目标函数,表示总配送成本最低;式(6)为车辆装载的货物总量不大于车辆的装载能力;式(7)为每辆车都从配送中心出发;式(8)为每个客户只由一辆车配送并且所有客户都得到服务;式(9)为车辆对客户服务完毕后,返回配送中心;式(10)和(11)表示变量之间的关系;式(12)和(13)表示满足客户要求的时间窗。 4.2 干扰管理模型的构建 4.2.1 问题描述 在某个客户的时间窗发生变化后,以各配送车辆所在位置作为虚拟的配送中心,是扰动后配送的起点,初始配送中心为配送的终点,即车辆对客户服务完毕后,返回初始配送中心。 另外,如果配送中心有多余的配送车辆,可以协助在途车辆进行配送,但实际上,配送中心往往并没有多余的配送车辆。因此,本文在制定调整方案时,假设剩余的任务只由原配送车辆完成。 4.2.2 参数及变量说明 m:未完成配送任务的客户总数量; V:客户点集合,V={v0,v1,…,vm+K},v0代表初始配送中心;v1,…,vm代表未完成配送任务的客户;vm+1,…,vm+K代表当前配送车辆所在的位置,即虚拟的配送中心; μ2:物流配送运营商对配送成本的不满意度; μ3:配送业务员对新路段个数的不满意度; 其他参数及变量与前文相同。 4.2.3 扰动的度量函数 (1) 客户扰动的度量 根据第2 节,对于客户而言,最关心的是货物的到达时间。因此,建立客户i的价值函数为: (14) 根据公式(3),客户i对货物到达时间的不满意隶属函数可表示为: (15) (2) 物流配送运营商扰动的度量 根据第2 节,对于物流配送运营商而言,在制定调整方案时最关心的是配送成本。因此,建立物流配送运营商的价值函数为: (16) 其中:选择现状,即没有发生扰动时,初始方案的总配送成本f0为参照点,如果调整方案的配送成本f>f0,意味着物流配送运营商亏损(x<0) ; 反之, 意味着物流配送运营商盈利(x≥0) 。 根据公式(3),物流配送运营商对配送成本的不满意隶属函数可表示为: (17) 其中:β2、λ2为参数;R2=f0+(1/λ2)1/β2。 (3) 配送业务员扰动的度量 根据第2 节,对于配送业务员而言,最关心的是配送路线的偏差,主要体现在新路段的个数上。 因此,建立配送业务员的价值函数为: V3(x)=-λ3(-x)β3,x<0 (18) 其中:由于初始方案中没有新路段,因此函数的参照点为0,如果调整方案的新路段个数g>0, 意味着配送业务员亏损(x<0) ;而g不可能小于0,说明配送业务员不可能盈利(x≥0) 。 根据公式(3),配送业务员对新路段个数的不满意隶属函数可表示为: (19) 其中:β3、λ3为参数;R3=(1/λ3)1/β3。 4.2.4 干扰管理模型 以各行为主体的扰动度量函数为基础,采用字典序多目标规划的方法,构建干扰管理模型如下: (20) P1≫P2≫P3 (21) (22) (23) (24) (25) ETi≤ti+wi≤LTii=1,…,m (26) 式(20)为目标函数,表示调整方案与初始方案的偏离最小,即系统的扰动程度最小。在本模型中,客户扰动之和的最小化为第一级目标,物流配送运营商扰动的最小化为第二级目标,配送业务员扰动的最小化为第三级目标;式(21)为不同目标的优先级,决策者可针对实际情况,调整不同目标的优先级顺序;式(22)为车辆装载的货物总量不大于车辆的装载能力;式(23)为每辆车都从虚拟的配送中心出发;式(24)为车辆对客户服务完毕后,返回初始配送中心;式(25)和(26)表示满足客户要求的时间窗。 由于干扰管理模型以初始方案的数学模型为基础,而该数学模型是NP-hard 的,因此干扰管理模型也是NP-hard 的。加之,干扰管理模型还需考虑干扰事件对整个物流配送系统的影响,相对来说更加复杂,求解起来也更加困难。而物流配送实时性很强,需要快速处理干扰事件。在这种背景下,由于蚁群算法具有正反馈、分布式计算以及贪婪的启发式搜索等特点,为求解上述问题提供了可能。但是,该算法仍然存在着容易陷入局部优化、搜索速度较慢等缺陷,因此本文提出改进的蚁群算法——混合蚁群算法(Hybrid Ant Colony Optimization, HACO),对干扰管理模型进行求解。 在HACO 中,采用信息素调整策略、最优个体交叉及变异策略来防止陷入局部优化,改善搜索结果;采用目标节点选择策略、集成其他算法策略来减少计算量,提高搜索速度。 5.1 信息素调整策略 (1)蚁群算法中,蚁群运动总是趋近于信息量最强的路径,但是如果该路径离最优解相差较远, 将会导致信息量得到不应有的增强,使得后续的蚂蚁难以发现更好的全局最优解,这说明信息量最强的路径不一定能反映出最优的路径。为了提高算法的全局搜索能力,本文采用确定性选择和随机性选择相结合的策略,即当搜索陷入局部最优时,对路径上的信息量进行动态调整,缩小最好和最差路径上信息量的差距,并适当加大随机选择的概率,以利于对解空间更完全地搜索。 (2)由于信息素的更新作用,每条路径上信息量可能在某次搜索后出现极大值或极小值的现象, 极大值将使搜索早熟,极小值则不利于全局搜索, 因此本文吸收了最值蚂蚁算法[16]的思想,将信息素水平限制在最大值和最小值之间,同时在搜索前, 将所有边的信息素水平设为最大值,从而使蚂蚁在搜索初期具有更大的搜索范围。另外,当各边信息素水平相差很大时,将各边信息素水平与信息素的最大值进行加权平均,从而使信息素差异相对减少,有利于产生新的搜索路线。 (3)当问题规模较大时,由于信息素保留系数ρ的存在,那些从未被搜索到的边,信息量会逐渐减小到接近于0,降低了算法的全局搜索能力。为解决这一问题,本文采用自适应改变ρ的方法[17]。 5.2 最优个体交叉及变异策略 遗传算法通过交叉和变异操作,能够增加种群的多样性,防止算法早熟。因此在HACO 中,通过借鉴上述思想,可有效扩大搜索空间,避免得到局部最优解。 (1)交叉策略 当搜索陷入停滞时,将最优个体和次优个体的编码进行交叉操作,假设两组编码分别为A1和A2, 交叉规则如下: ①随机生成交叉段的长度和交叉段起始位置。假设A1:B1|B2|B3,A2:C1|C2|C3,B2和C2分别为A1和A2的交叉段; ②将C2插入到A1中,位于B2前面,这样形成新的编码A3:B1|C2|B2|B3; ③在A3中,删除B1、B2、B3中与C2重复的节点,从而形成新的交叉编码A3; ④对A2采用相同的方法,生成新的编码A4; ⑤从A1、A2、A3、A4中选出最优编码。 (2)变异策略 当算法倾向于局部收敛时,对最优个体进行变异,即在这个局部最优路径上取任意一段或几段, 让信息素减少至最小值。于是下次不得不跳出此路径,而去寻找另外可能的更好路径。实验表明,对于规模较大的问题,在引入变异后可明显看到求解结果出现震荡,然后向更好解的方向变化。 5.3 目标节点选择策略 对于一个较复杂的最短路径问题,节点i在选择下一个旅行节点j时,不可能是离i较远的那些节点。而蚁群算法中,蚂蚁在选择下一个节点时, 需要计算所有未走过节点的转移概率,耗费较长的计算时间。 根据上述分析,蚂蚁对下一个节点的选择仅局限于离当前节点较近的部分节点,只对这些节点计算转移概率即可,这样能大幅度提高算法的搜索速度。因此本文引入目标节点选择策略,其原理是分别以n个节点为起点,根据该节点与其他n-1个节点的距离,建立n个距离由短到长的排序表,选择其中前若干个建立该节点的候选节点列表,蚂蚁对下一个节点的选择只在候选节点列表中产生。 5.4 集成其他算法策略 蚁群算法易与传统启发式算法相结合的特点, 决定其具有很强的耦合性,因此将节约法、交换法两种简洁高效的优化算法集成到蚁群算法中,可大幅度提高算法的求解速度。 由于物流配送干扰管理问题尚未有标准的测试数据集,因此,算例验证包括两部分:第一部分采用测试题库对算法进行测试;第二部分首先设计一个具体算例,以配送成本最低为目标,得到初始方案。之后将此方案作为客户时间窗变化的物流配送干扰管理问题的背景,运用本文方法进行求解。通过与全局重调度方法、局部重调度方法的结果进行对比,验证本文方法的有效性。 6.1 算法验证 (1) 实验结果 本节采用典型的测试题库——Benchmark Problems[18]对算法进行测试。在该题库所列的六类例题中,每一类随机选取两个问题组成测试数据集,采用传统蚁群算法(ACO)、改进蚁群算法[19-20]、改进遗传算法[21]、改进禁忌搜索算法[22]和HACO算法进行求解,如表1 所示。 (2)对比分析 在求解上述12 个例题中,根据表1 的实验结果,HACO 得到的结果100%优于传统蚁群算法得到的结果,92%优于或接近于改进蚁群算法——IACS-SA 得到的结果,75%优于或接近于改进蚁群算法——MACS-IH 得到的结果,100%优于或接近于改进遗传算法——GenSAT 得到的结果,92%优于或接近于改进禁忌搜索算法——SATabu 得到的结果。 分析结果表明,HACO 的求解结果已有部分优于文献中已有的最好结果, 特别是在RC1-03 上表现显著,其他则与最好结果非常接近,因此HACO 在求解NP-hard 问题时是非常有竞争力的。由于HACO 中的参数选择是凭多次试验而定的,没有理论依据,因此求出的解不是算法所能取得的最好解。将算法中各参数设置成最优,其最终解还有进一步改进的余地。 表1 HACO 和其他算法的实验结果 6.2 干扰管理模型验证 (1)算例设计 某配送中心坐标为(0.7,0.7),在0 时向周围的24 个客户配送货物,为计算方便,假设客户的信息无量纲,如表2 所示。设车辆的装卸货时间不计,即服务时间为0。 根据上述条件,得出初始方案的配送路线如下。路线1:0→19→16→20→11→12→6→ 22→23→13→14→7→0;路线2:0→3→9→10→1→17→8→24→0;路线3:0→21→18→15→5→2→4→0。此时总配送成本为5.7,即目标函数最优。 (2)实验结果 本节采用两种情况来评价干扰管理模型, 即: 情况1:当t=0.25时,客户12 的时间窗由[0, 1.5]变为[1.3, 3]; 情况2:当t=0.3时,客户1 的时间窗由[1, 2]变为[1.5, 2.5]。 根据Tversky 等[15],取β=0.88、λ=2.25。分别采用本文方法、全局重调度方法和局部重调度方法进行求解,结果如表3 所示。 (3)对比分析 对表3进行分析,得出的主要结论如下: ①从客户的扰动来看,本文方法得到的结果明显优于其他两种方法得到的结果, 这说明干扰管理模型在降低客户不满意度上的效果是非常显著的; ②从物流配送运营商的扰动来看,本文方法得到的结果劣于其他两种方法得到的结果,但是相差不多,说明干扰管理模型得到的配送成本在物流配送运营商可以接受的范围之内; ③从配送业务员的扰动来看,本文方法得到的结果与其他两种方法得到的结果相同,这说明干扰管理模型在抑制配送路线的偏差上不劣于其他两种方法。 综上,在考虑人的行为因素的情况下,本文方法以牺牲较小的配送成本,换来了客户不满意度较大幅度的降低。因此, 与全局重调度方法和局部重调 表2-1 客户信息 表2-2 客户信息 表3 不同方法的求解结果 度方法相比,本文方法得到的结果更为实用。另外,虽然从短期看,物流配送运营商牺牲了一定的成本,但从长期的战略角度看,有利于拥有稳定的客户群并吸引更多的新客户,进而扩大企业的影响力,促进企业的可持续发展。 本文针对客户时间窗变化的物流配送干扰管理问题,结合行为科学、运筹学等相关理论, 做了较深入的研究工作,具体体现在: (1) 提出客户时间窗变化问题基于行为的扰动度量方法,为物流配送系统中涉及人的行为感知的扰动度量提供了新工具,为解决干扰管理领域扰动度量这一关键问题提供了新思路。 (2) 将人的行为因素考虑在内,构建物流配送干扰管理的多目标优化模型,并提出改进的蚁群算法——混合蚁群算法的基本原理,为快速求解干扰管理模型这一NP-hard 问题提供了新思路,为寻找扰动最小的物流配送调整方案提供较为实用的定量分析工具。 本文方法在理论层面上,通过将人的行为因素考虑在内,能够获得较为实用的扰动最小的调整方案,这不仅有利于丰富干扰管理理论和方法,也能够促进行为运筹学、行为运作管理等新兴学科的发展;在实际层面上,本文构建的干扰管理模型具有较强的实际操作性,各个目标之间的优先级别能够非常灵活地进行转变,适用范围较广泛,这有利于促进现代物流产业的发展。 为了研究的方便,本文采用Tversky 和Kahneman[14-15]给出的β、λ 值进行算例验证,如何确定上述参数的实际值,从而完善物流配送干扰管理模型,是下一步研究的重点。另外,物流配送系统中存在着大量的干扰事件,客户时间窗变化仅仅是众多干扰事件之一,如何将本文方法进一步深化,使其应用于需求变动、运力受扰等其他干扰事件的处理,也是值得研究的重要方向,有利于干扰管理的发展与普及。 [1] 杨文超, 胡祥培, 王征. 顾客时间窗变化的物流配送问题干扰管理方法研究[J]. 大连理工大学学报, 2012, 52(2): 290-296 [2] Yu Gang, Qi Xiantong. Disruption management: Framework, models and applications [M].Singapore: World Scientific Publishing, 2004. [3] Clausen J, Larsen A, Larsen J, et al.. Disruption management in the airline industry-concepts, models and methods[J]. Computers & Operations Research, 2010, 37(5): 809-821. [4] Jiang Yang, Sun Wei, Ding Qiulei, et al. A model of disruption management for solving machine disruption in single machine scheduling[J]. ICIC Express Letter, 2012, 6(12): 3143-3148. [5] Qi Xiangtong, Bard J F, Yu Gang. Supply chain coordination with demand disruptions[J].Omega, 2004, 32(4): 301-312. [6] Zhu Guidong, Bard J F, Yu Gang. Disruption management for resource-constrained project scheduling[J]. Journal of the Operational Research Society, 2005, 56(4): 365-381. [7] Wang H F, Wen Yupin. Time-constrained Chinese postman problems[J]. Computers & Mathematics with Applications, 2002, 44(34): 375-387. [8] 王明春, 高成修, 曾永廷. VRPTW的扰动恢复及其TABU SEARCH算法[J]. 数学杂志, 2006, 26(2): 231-236. [9] 钟石泉, 杜纲, 贺国光. 有顾客时间窗和发货量变化的紧急车辆调度研究[J]. 管理工程学报, 2007, 21(4): 114-118. [10] 王旭坪, 许传磊, 胡祥培. 有顾客时间窗和发货量变化的车辆调度干扰管理研究[J]. 管理科学, 2008, 21(5): 111-120. [11] Hadjar A, Soumis F. Dynamic window reduction for the multiple depot vehicle scheduling problem with time windows[J]. Computers & Operations Research, 2009, 36(7): 2160-2172. [12] 王征, 王建军, 杨文超. 顾客时间窗变化的多车场车辆调度干扰管理模型研究[J]. 管理科学, 2010, 23(3): 103-112. [13] 王旭坪,阮俊虎,张凯,等. 有模糊时间窗的车辆调度组合干扰管理研究[J]. 管理科学学报, 2011, 14(6): 2-15. [14] Kahneman D, Tversky A. Prospect theory: An analysis of decision under risk[J]. Econometrica, 1979, 47(2): 263-291. [15] Tversky A, Kahneman D. Advances in prospect theory: Cumulative representation of uncertainty[J]. Journal of Risk and uncertainty, 1992, 5(4): 297-323. [16] Stützle T, Hoos H. Improvements on the ant system: Introducing MAX-MIN ant system [M]//Kurkova V,Steele N C,Neruda R,et al.Artificial Neural Networks and Genetic Algorithms, Vienna:Springer,1998. [17] 王颖,谢剑英. 一种自适应蚁群算法及其仿真研究[J]. 系统仿真研究, 2002, 14(1): 31-33. [18] Solomon M M. Algorithms for the vehicle routing and scheduling problems with time window constraints[J]. Operations research, 1987, 35(2): 254-265. [19] Chen C H, Ting C J. A hybird ant colony system for vehicle routing problem with time windows[J]. Journal of the Eastern Asia Society for Transportation Studies, 2005, 6: 2822-2836. [20] Balseiro S R, Loiseau I, Ramonet J. An ant colony algorithm hybridized with insertion heuristics for the time dependent vehicle routing problem with time windows[J]. Computers & Operations Research, 2011,38(6): 954-966. [21] Thangiah S R, Osman I H, Sun Tong. Hybrid genetic algorithm, simulated annealing and tabu search methods for vehicle routing problems with time windows[R]. Technical Report, Institute of Mathematics & Statistics, University of Kent, Canterbury, UK, 1994. [22] Tan K C, Lee L H, Ou K. Artificial intelligence heuristics in solving vehicle routing problems with time window constraints. Engineering Applications of Artificial intelligence, 2001, 14(6): 825-837. Model of Disruption Management for the Change of Time Window Based on Human Behavior in Logistic Distribution DING Qiu-lei (School of Business Administration, Dongbei University of Finance and Economics, Dalian 116025, China) It is difficult to generate the new plan effectively for minimizing the negative impact when the time window of customer changes in logistic distribution. Based on disruption management, this research aims to improve the science of the decision making of disruption management in logistic distribution by combining the behavioral perception in prospect theory with the quantitative analysis in operations research. At the beginning, the method to measure the deviation based on prospect theory is studied by analyzing the effects of the change of time window on customers, logistics providers and drivers. Then, the multi-objective model of disruption management is constructed and an improved ant colony optimization is demonstrated. The computational result of the model proves that, due to the tradeoff between all parties involved in logistic distribution, our approach is more practical than global rescheduling and local rescheduling. This research contributes to the theory and method of disruption management, which can be used in other fields, such as production planning problems, flight scheduling, supply chain management, etc. management engineering; logistic distribution; disruption management; prospect theory; multi-objective optimization 1003-207(2015)05-0089-09 10.16381/j.cnki.issn1003-207x.2015.05.012 2013-04-09; 2013-10-27 国家自然科学基金资助项目(71301020);辽宁省教育厅优秀人才项目(WJQ2014030);辽宁省教育厅科学研究一般项目(L2014216) 丁秋雷(1980-),男(汉族),山东汶上人,东北财经大学工商管理学院,博士,讲师,研究方向:干扰管理、电子商务与物流管理、生产运作管理. C93;TP18 A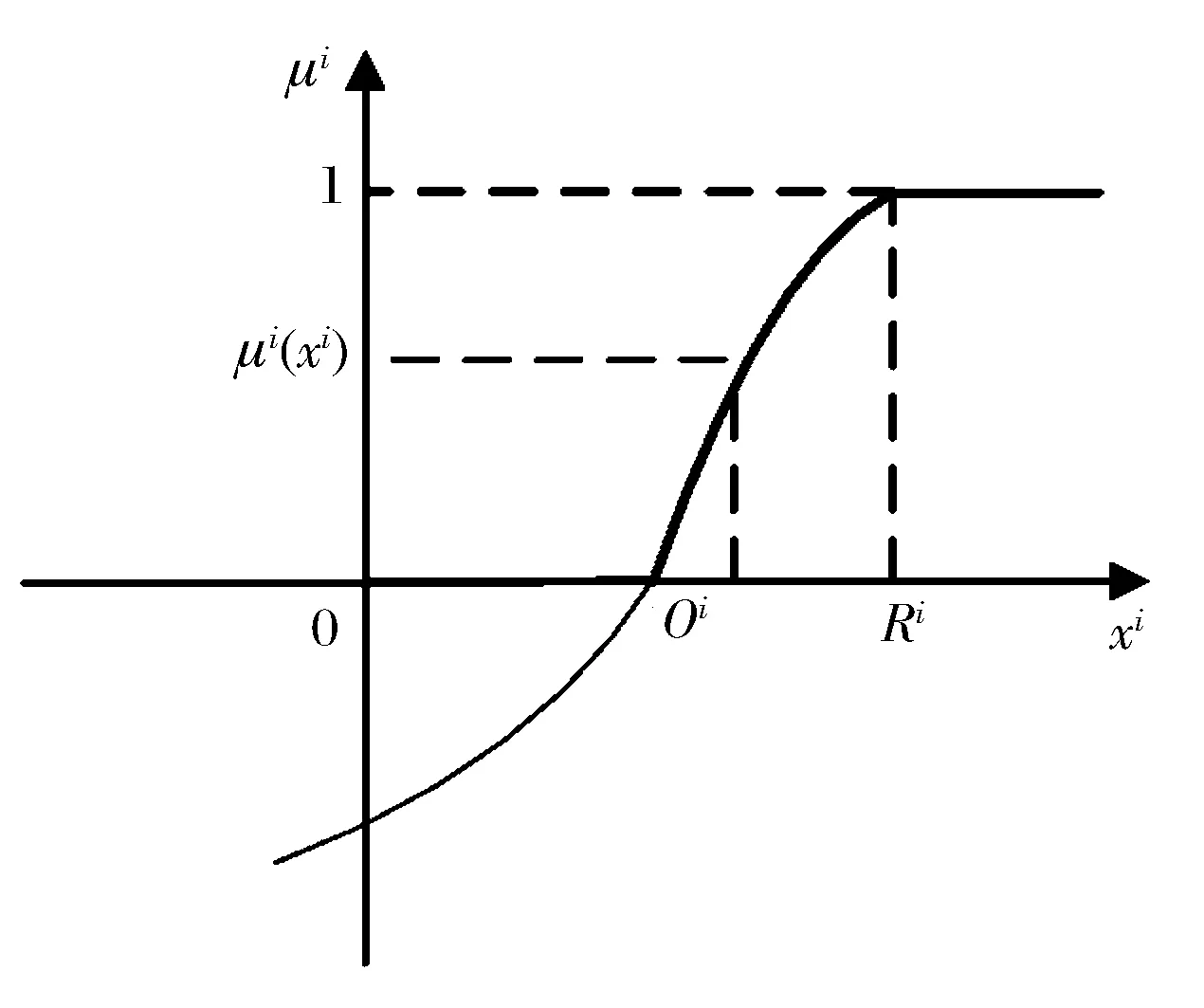
4 客户时间窗变化的物流配送干扰管理模型



5 干扰管理模型的求解方法研究
6 算例验证及结果分析




7 结语
