考虑交易成本的多阶段投资组合评价方法研究

周忠宝，刘 佩，喻怀宁，马超群，刘文斌,2

(1. 湖南大学工商管理学院，湖南 长沙 410082；2. Business School, University of Kent, Kent, CT2 7PE)



考虑交易成本的多阶段投资组合评价方法研究

周忠宝1，刘 佩1，喻怀宁1，马超群1，刘文斌1,2

(1. 湖南大学工商管理学院，湖南 长沙 410082；2. Business School, University of Kent, Kent, CT2 7PE)

多阶段投资组合评价是目前研究的热点问题，本文将交易成本考虑进去，构建了考虑交易成本的多阶段投资组合优化模型，基于真实前沿面定义了投资组合的效率并构建了相应的非线性模型进行计算。针对非线性模型难以求解及真实前沿面解析解难以获得等问题，本文证明了前沿面函数为凹函数，进而利用DEA模型的前沿面来逼近真实前沿面并估计多阶段投资组合的效率，最后通过仿真分析验证了本文方法的有效性。

多阶段投资组合；交易成本；绩效评价；数据包络分析

1 引言

证券投资组合的主要任务是进行有效的资产配置，从而实现最大化收益、最小化风险的投资目标。1952年，Markowitz首次采用收益率的方差度量投资组合的风险，并建立了均值-方差优化模型[1]，为投资组合理论的发展奠定了坚实的基础。Markowitz投资组合理论表明，投资者在进行证券投资时可以根据收益和风险两个指标进行权衡选择，即在期望收益相同的情况下，选择风险较低的投资组合，在投资风险相同的情况下，选择期望收益较高的投资组合。

在实际金融市场活动中，投资者需要根据投资环境的变化适时地调整投资组合头寸。因此，许多学者将Markowitz均值-方差模型扩展到多阶段的情形[2-4]。Li Duan和Ng[5]推导出了多阶段均值-方差模型的解析最优解。宿洁和刘家壮[6]将多阶段投资组合优化模型转化为线性动态规划模型。Sun Jun[7]等学者提出运用漂移粒子群算法来求解多阶段投资组合优化问题，并将该算法与粒子群优化算法和遗传算法进行比较，结果表明漂移粒子群算法优于其他几种算法。Liu Yongjun等[8]学者研究了模糊多阶段投资组合优化问题，并运用模糊决策理论和多目标规划方法将问题转化为非线性规划，用一种改进的粒子群优化算法来对模型进行求解。

上述多阶段研究中并未考虑交易成本这一重要的市场摩擦因素，Kamin[9]将交易成本引入动态投资组合优化模型中，并说明投资者的投资行为在有无交易成本的情形下完全不同。Yi Lan[10]通过引入一组辅助鞅，将考虑交易成本的多阶段投资组合优化问题与无交易成本的优化问题进行了对比分析。Zhang Weiguo等[11]学者在考虑投资回报、风险、交易成本和投资组合的多元化程度等指标的情况下，构建了可能性均值-半方差-熵的多阶段投资组合模型，并通过混合智能算法获得最优投资策略。Wang Zhen和Liu Sanyang[12]研究了考虑固定比例交易成本的多阶段均值-方差投资组合优化问题，并通过引入拉格朗日乘子和定义间接效用函数来解决投资组合优化问题。上述多阶段投资组合优化模型虽然考虑了交易成本，但是，模型的推导过程相当复杂，计算量也非常大，在实际应用中有一定的难度。

数据包络分析(Data Envelopment Analysis, DEA)[13-14]作为一种经济学中常用的效率评价方法，近年来被广泛应用于投资组合评价问题。然而现有研究普遍将交易成本作为一个输入指标，直接构建DEA模型进行分析，缺乏理论依据和说服力，而且研究也仅以单阶段投资组合评价问题为主，较少考虑投资组合的多阶段动态特征。

考虑投资组合交易成本和多阶段动态特征进行评价，能够更准确地比较投资组合的优劣，这不仅可以为投资者提供决策参考意见，而且可以为管理者提供投资组合优化改进方向。本文首先建立了考虑交易成本的多阶段投资组合优化模型，基于真实前沿面定义了多阶段投资组合的效率和非线性效率评价模型。考虑到真实前沿面的解析解难以获得，非线性模型的求解也非常困难，本文在证明了优化模型的前沿面为凹函数的基础上，用DEA前沿面来逼近真实前沿面，进而用DEA效率来估计真实效率。仿真分析的结果表明，在考虑交易成本的情况下，DEA模型可以较好地估计多阶段投资组合的效率。

2 考虑交易成本的多阶段投资组合优化和评价模型

2.1 考虑交易成本的多阶段投资组合优化模型

对投资者而言，他们最关心的莫过于证券投资的收益回报率。然而，投资者进行证券交易时所需缴纳的委托费、印花税、佣金和过户费等是其证券投资过程中必不可少的支出，本文将证券交易过程中发生的这些费用统称为交易成本。事实上，偏高的交易成本对投资者的收益具有严重的侵蚀作用，尤其是当初始资金量较少时，资金的分散化投资可能导致偏高的交易成本。因此，交易成本是投资者进行决策时不容忽视的一个重要因素。

本文以Calafiore[15]提出的Open-loop多阶段投资组合优化问题为基础。Open-loop控制策略也叫无反馈控制策略(Non-feedback control)，它假定投资者在投资期初就计算和固定了整个投资过程中各阶段的最优投资策略，其特点是计算输入系统时只使用系统的当前状态，而不使用反馈来确定输出是否达到了预期目标。根据Calafiore的研究，本文假定投资策略为确定型变量，采用Open-loop控制策略来寻求多阶段投资组合优化模型在平均意义下的最优解。

maxE(RT)

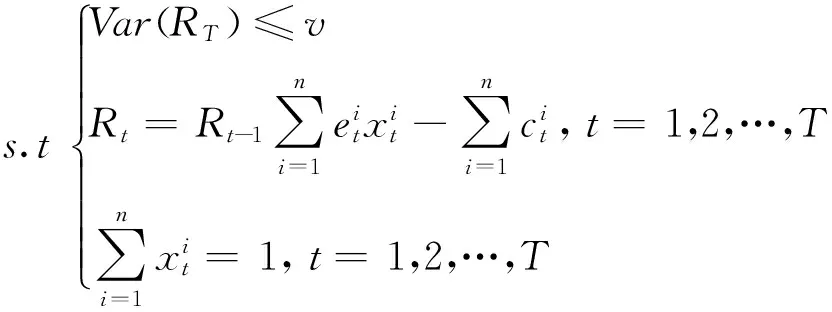
(1)

需要特别说明的是，模型(1)并没有限定收益测度和风险测度的具体形式，从而使得其更具有一般性，如果收益测度为最终财富的期望、风险测度为最终财富的方差，则对应于常用的均值-方差模型。

类似地，可以建立在给定收益水平下，最小化风险的优化模型，进而采用文中的思路构建相应的风险导向的评价模型，限于篇幅，不再赘述。

本文假定交易成本是一次性产生的，且不具有时间价值，接下来主要考虑三种常见的凸交易成本，即线性交易成本、V型交易成本和分段线性凸交易成本这三种情形：

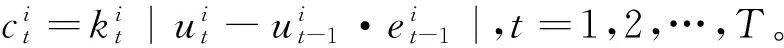
分段线性凸交易成本假设第i种资产的交易成本是交易额的分段线性函数，且为凸函数。K段线性凸交易成本可表示为：

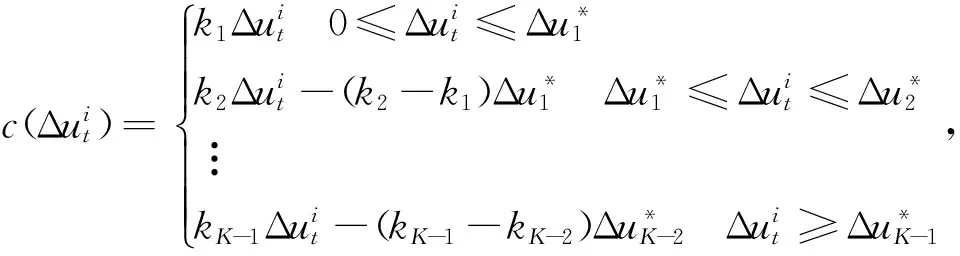
kj≥0,j=1,…,K-1

2.2 考虑交易成本的多阶段投资组合效率的定义

根据优化模型(1)，可以得到第T阶段末最终收益-风险前沿面，根据经典经济学中技术效率的定义，可以将待评价投资组合投影到该前沿面上，进而根据投资组合与投影点的距离来评价投资组合的效率。在图1中，横坐标为风险测度，纵坐标为收益测度，曲线AB为Open-loop多阶段投资组合优化模型的前沿面，P表示某一待评价的投资组合。

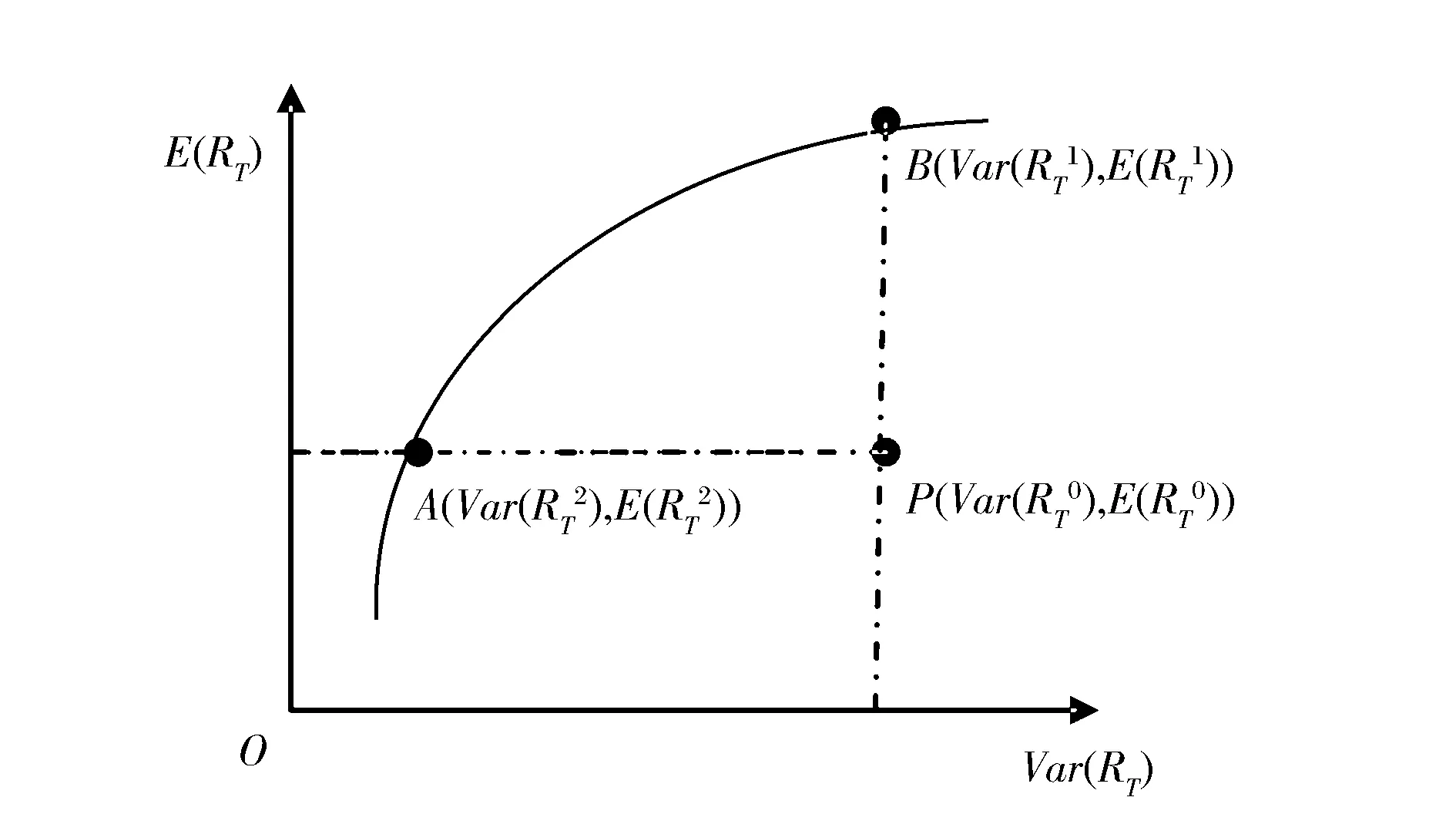
图1 多阶段投资组合的效率

根据上面的讨论，我们可以基于多阶段投资组合真实前沿面来定义两种类型的效率：

定义1：多阶段投资组合的效率

2.3 考虑交易成本的多阶段投资组合评价模型

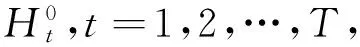
根据优化模型(1)，可以建立收益导向下的多阶段投资组合效率评价模型：

maxφ

(2)

投资组合效率的计算依赖于投资组合优化模型(1)的前沿面，然而，前沿面的解析解难以获得。此外，模型(2)是随机非线性规划模型，求解异常困难。鉴于此，本文接下来将证明投资组合优化模型(1)的前沿面为凹函数，以此为基础，用DEA前沿面来逼近真实前沿面，进而用DEA模型来估计投资组合的效率。

3 考虑交易成本的多阶段投资组合DEA评价方法

3.1 考虑交易成本的多阶段投资组合前沿面的凹性

在模型(1)中，et是定义在概率空间(Ω,F,P)上的实值随机向量，表示资产在第t阶段的收益率。xt为决策变量，表示资产在第t阶段的投资比例，其构成的集合Π为决策空间。由最终财富的产生过程可知，随机向量泛函RT是关于xt和et的函数。在Open-loop投资组合优化模型(1)中，随机向量泛函RT的随机性只与收益率et有关。一般假定et为连续型随机变量，根据决策空间Π的凸性可知，从而可以假定随机向量泛函RT为连续型随机变量，且RT能取遍实数轴某段区间上的所有实数点，即RT构成的集合为凸集。

定义2： 风险测度与收益测度的凸凹性

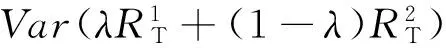
成立，则称Var为定义在Θ上的凸风险测度。如果有：

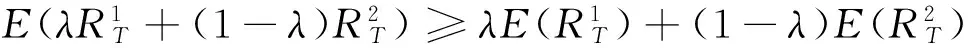
定理1：当风险测度Var(RT)为定义在Θ→R上实值可测的凸函数，收益测度E(RT)为定义在Θ→R上实值可测的凹函数，且随机向量泛函RT构成的集合Θ为凸集，则模型(1)所确定的前沿面是凹函数。

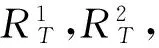
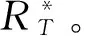
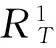
根据凹函数的定义可知f(v)是凹函数，即模型(1)确定的前沿面是凹函数。

3.2 考虑交易成本的多阶段投资组合DEA评价模型

上一小节证明了考虑交易成本的多阶段投资组合优化模型(1)的前沿面为凹函数，根据Banker等[14]的逼近性原理，当前沿面为凹函数(生产可能集为凸集)时，随着样本量的增加，DEA模型的前沿面将逐渐逼近真实的前沿面。基于此，我们可以构建相应的DEA模型来评价考虑交易成本的多阶段投资组合的效率。

考虑交易成本的多阶段投资组合效率评价DEA模型(收益导向)可以表示为：

maxφj0

(3)

4 仿真分析

本文仿真分析将采用LiDuan和Ng[5]的数据，假定投资期间T=2，初始财富R0=1，并假设证券市场上有三种资产，资产在各阶段的统计特性如下：

E(et)=[1.162,1.246,1.228]，t=1,2

在接下来的仿真分析中，我们以最终财富的期望为收益测度，以最终财富的方差为风险测度。

当交易成本为线性交易成本时，资产是不允许卖空的。假定买入时交易费率为1%，即：

kt=[0.01, 0.01, 0.01]，t=1,2

当交易成本为V型交易成本时，资产是允许卖空的，同样假定资产买卖时交易费率为1%，即：

当交易成本为分段线性凸交易成本时，资产是不允许卖空的。假设交易成本分为两段，交易费率分别为：

图2-图4给出了不同类型交易成本下，不同样本量DEA前沿面的比较图。由图可知，当投资组合样本量逐渐增大时，DEA前沿面越来越靠近于真实前沿面。且样本量为5000时的DEA前沿面与样本量为2000时的DEA前沿面几乎重合。因此，根据Banker等[14]学者的逼近性原理，我们可以用样本量为5000时的DEA前沿面来近似地作为真实前沿面。

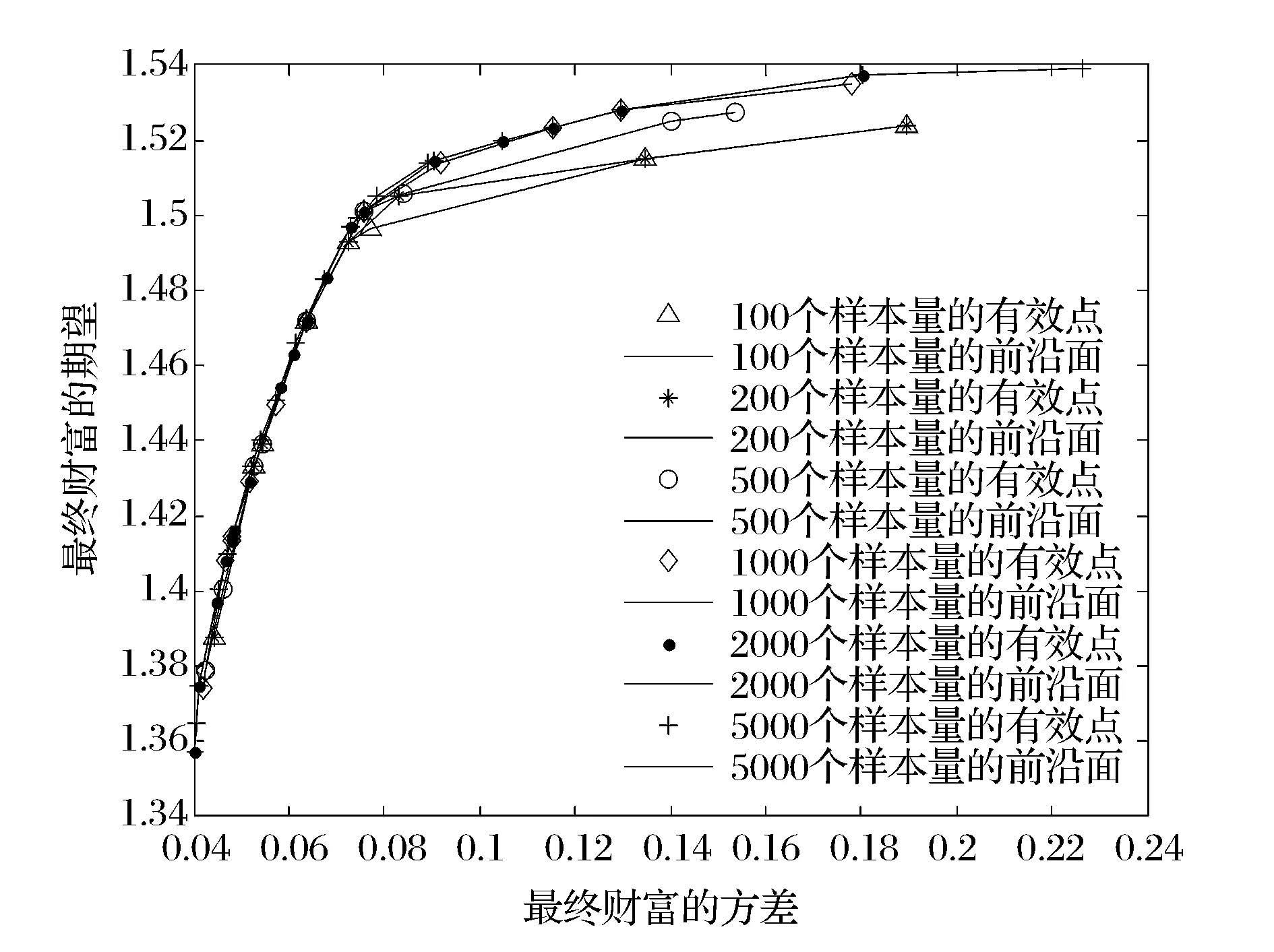
图2 线性交易成本下的前沿面比较

图3 V型交易成本下的前沿面比较

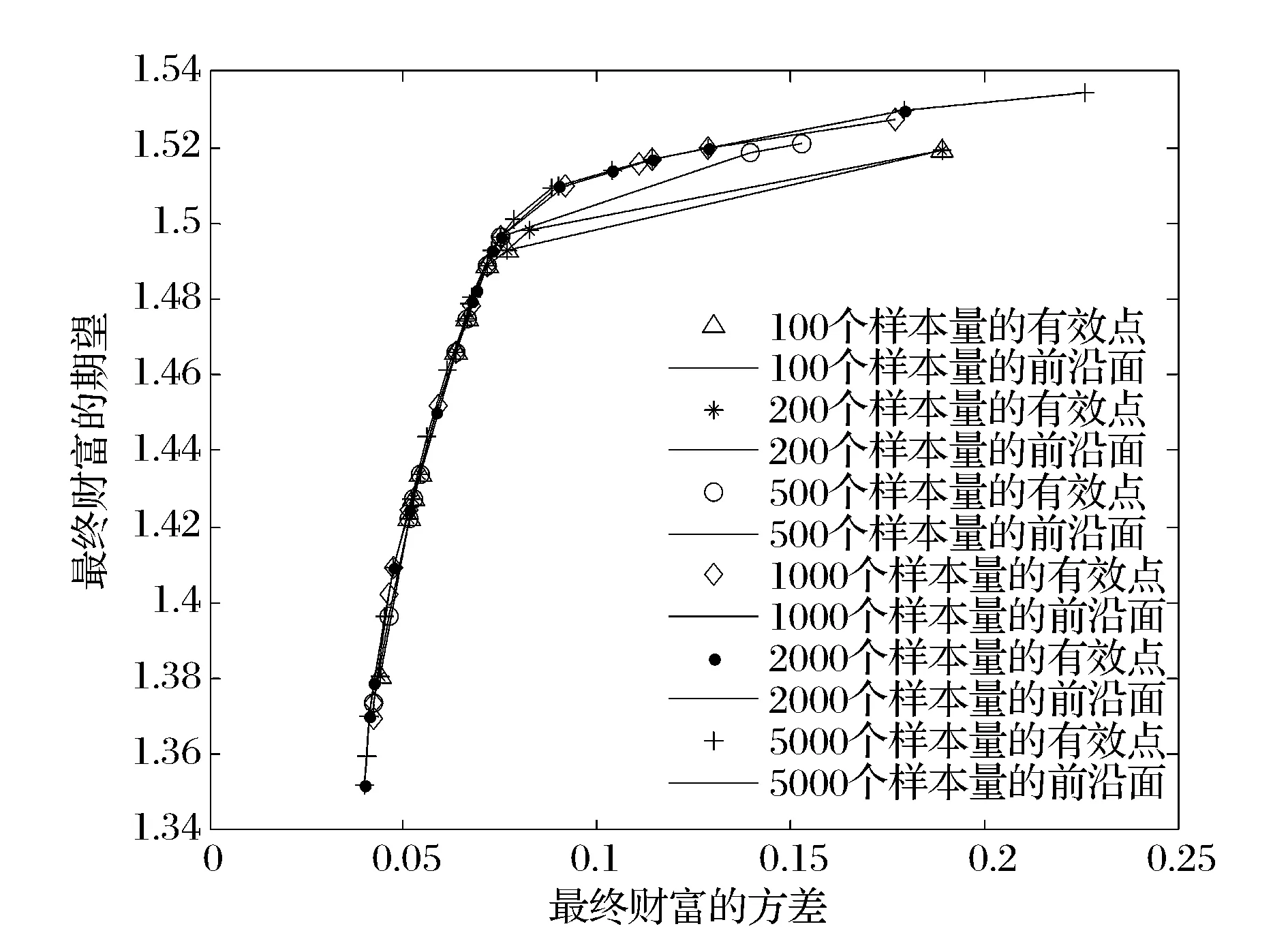
图4 分段线性凸交易成本下的前沿面比较

以样本量5000时的DEA前沿面作为近似前沿面，分别将100、200和500组投资组合作为待评价的决策单元，投影到该近似前沿面上，进而根据定义1计算投资组合的效率。然后直接利用DEA模型(3)计算100、200和500组投资组合的效率。两种方法计算出来的效率的相关系数和效率排名的相关系数如表1-表3所示。

表1 线性交易成本下的相关性分析(收益导向)

表2 V型交易成本下的相关性分析(收益导向)

表3 分段线性凸交易成本下的相关性分析(收益导向)

由表1-表3可知，基于近似前沿面计算的效率与DEA模型估计的效率之间的相关系数均在0.9以上，且效率排名的相关系数也比较高，表明采用DEA模型评价考虑交易成本的多阶段投资组合的效率是可行的。

经过多次仿真分析，我们发现，对于线性交易成本、V型交易成本和分段线性凸交易成本，当样本量足够大时，基于数据的DEA前沿面的变动幅度越来越小，几乎重叠。且样本量越大，所形成的投资组合可能集越大。另外，基于数据的DEA模型计算的效率与依据多阶段投资组合效率定义所计算的效率有很高的相关性。这都表明DEA模型可以较好地估计考虑交易成本的多阶段投资组合的效率。

5 结语

本文假定投资策略为确定型变量，通过累积财富将各阶段联系起来，建立了最大化最终收益和最小化风险的Open-loop多阶段投资组合优化模型。基于优化模型的真实前沿面，给出了多阶段投资组合在收益导向和风险导向下效率的具体定义，并构建了不同导向下的多阶段投资组合效率评价模型。考虑到真实前沿面的解析解难以获取，效率评价模型的随机非线性特征等实际应用中的问题，本文证明了优化模型的前沿面为凹函数，以此为基础用DEA前沿面来逼近真实前沿面，构建了收益导向和风险导向的DEA模型来评价考虑交易成本的多阶段投资组合的效率。由于DEA模型是线性规划模型，因而可以大大降低求解的复杂度。仿真分析的结果表明，DEA模型可以较好地估计考虑交易成本的多阶段投资组合的效率，具有较强的实用性。

[1] Markowitz H M. Portfolio selection[J]. Journal of Finance, 1952, 7(1): 77-91.

[2] Mossin J. Optimal multiperiod portfolio policies[J]. Journal of Business, 1968, 41(2): 215-229.

[3] Dumas B, Luciano E. An exact solution to a dynamic portfolio choice problem under transactions costs[J]. The Journal of Finance, 1991, 46(2): 577-595.

[4] Pliska S R. Introduction to mathematical finance[M]. Oxford UK: Blackwell publishers, 1997.

[5] Li Duan, Ng W L. Optimal dynamic portfolio selection: Multiperiod mean-variance formulation[J]. Mathematical Finance, 2000, 10(3): 387-406.

[6] 宿洁,刘家壮.多阶段资产投资的动态规划决策模型[J].中国管理科学, 2001, 9(3): 55-61.

[7] Sun Jun, Fang Wei, Wu Xiaojun, et al.Solving the multi-stage portfolio optimization problem with a novel particle swarm optimization[J]. Expert Systems with Applications, 2011, 38(6): 6727-6735.

[8] Liu Yongjun, Zhang Weiguo, Zhang Pu. A multi-period portfolio selection optimization model by using interval analysis[J]. Economic Modelling, 2013, 33: 113-119.

[9] KaminJ H. Optimal portfolio revision with a proportional transaction cost[J]. Management Science. 1975, 21(11), 1263-1271.

[10] Yi Lan. Multi-period portfolio selection with transaction costs[C].Proceedings of 2nd IEEE International Conference on Information and Financial Engineering,Chongqing,China,September 17-19,2010.

[11] Zhang Weiguo, Liu Yongjun, Xu Weijun. A possibilistic mean-semi variance-entropy model for multi-period portfolio selection with transaction costs[J]. European Journal of Operational Research, 2012, 222(2): 341-349.

[12] Wang Zhen, Liu Sanyang. Multi-period mean-variance portfolio selection with fixed and proportional transaction costs[J]. Journal of industrial and management optimization, 2013, 9(3): 643-657.

[13] Charnes A, Cooper W W, Rhodes E. Measuring the efficiency of decision making units[J]. European journal of operational research, 1978, 2(6): 429-444.

[14] Banker R D, Charnes A, Cooper W W. Some models for estimating technical and scale inefficiencies in data envelopment analysis[J]. Management Science, 1984, 30(9): 1078-1092.

[15] Calafiore G C. Multi-period portfolio optimization with linear control policies[J]. Automatica, 2008, 44(10): 2463-2473.

Performance Evaluation of Multi-period Portfolios on Considering Transaction Costs

ZHOU Zhong-bao1，LIU Pei1,YU Huai-ning1,MA Chao-qun1,LIU Wen-bin2,1

(1. School of Business Administration, Hunan University, Changsha 410082, China;2. Business School, University of Kent, Kent, CT2 7PE, England)

Multi-period portfolio evaluation is a hot topic in financial studies. By taking transaction costs into consideration, a multi-period portfolio optimization model is proposed. Based on the real frontier, the definition of multi-period portfolio efficiency and the corresponding nonlinear model are constructed. Due to the lack of analytical solutions of frontier and difficulties in solving the nonlinear model, it is proved that the true portfolio frontier is concave, and then DEA model is used to approximate the frontier and estimate the efficiencies of multi-period portfolios with transaction costs. The validity of the proposed method is illustrated by simulation in the end.

multi-period portfolios; transaction costs; performance evaluation; data envelopment analysis

1003-207(2015)05-0001-06

10.16381/j.cnki.issn1003-207x.2015.05.001

2014-03-19；

2014-09-02

国家自然科学基金资助项目(71371067，71431008);国家社会科学基金资助项目(12CGL023)

周忠宝(1977-)，男(汉族)，山东齐河人，湖南大学工商管理学院教授，博士生导师，研究方向：金融工程与风险管理、系统优化与决策.

F830.59

A