单兵装甲下肢外骨骼机器人设计与仿真分析
2015-06-12晁智强张传清韩寿松
晁智强, 王 飞, 2, 张传清, 韩寿松
(1. 装甲兵工程学院机械工程系, 北京 100072; 2. 66336部队, 河北 高碑店 074000)
单兵装甲下肢外骨骼机器人设计与仿真分析
晁智强1, 王 飞1, 2, 张传清1, 韩寿松1
(1. 装甲兵工程学院机械工程系, 北京 100072; 2. 66336部队, 河北 高碑店 074000)
设计了一种针对军事用途的单兵装甲下肢外骨骼机器人(Individual Soldier Armored Lower Extremity Exoskeleton, ISALEE),发挥人与机械各自优势,提高士兵在执行任务过程中的承载能力。通过建立5连杆模型,对人体行走步态及下肢自由度进行了分析。利用零力矩点(Zero Moment Point, ZMP)稳定判据,分析单兵装甲下肢外骨骼的动态稳定性,并对步态进行规划。最后利用CAD软件Solidworks和动力学仿真软件ADAMS对单兵装甲下肢外骨骼进行虚拟样机建模和仿真。仿真结果验证了利用ADAMS虚拟样机进行结构设计的可行性,并为液压驱动元件的选型和减小膝关节负载压力的设计提供了理论依据。
下肢外骨骼; 零力矩点; 步态规划; 仿真
单兵装甲机器人是仿人机器人的一个特殊应用,使用时“穿”在人体外侧,构成一套人体的“外骨骼”系统。单兵装甲机器人可增强人的体能,提供装甲防护,可应用于环境狭小、恶劣,不便于重型机械展开而不得不需要人力完成的各种作战、修筑、运输或抢险救灾等场所。从军用角度进行分析,单兵装甲机器人的应用将会十分广泛[1]。美国加州大学伯克利分校的下肢外骨骼(Berkeley Lower Extremity Exoskeleton, BLEEX)是世界上首个可实际应用的智能负载外骨骼机器人;雷神公司研制的第2代外骨骼装置Exoskeleton-2(XOS-2)因其强大的负载能力和动力而闻名。国内对下肢外骨骼的研究单位主要有浙江大学、哈尔滨工业大学等[2-5],但仍处于理论研究和样机实验阶段,并未投入实际应用。
当前国内外研究主要集中在如何增强穿戴者的力量,而对于降低外骨骼能耗和穿戴者膝关节负载方面的研究鲜见报道。BLEEX由于其能耗大,穿戴者长时间使用会导致膝盖不舒服,因此未获得进一步资助;XOS-2也因自带电池仅能使用40 min,导致其始终离不开地面供电,至今未能投入使用。因此,在当前便携电源续航技术发展遇到瓶颈的情况下,如何能够降低能耗是决定外骨骼能否更好地投入实战应用的重要因素。Grifn等[6]研究发现:当外骨骼负载增加40%时,踝关节、膝关节和髋关节的转动力矩峰值分别增加38%、98%和47%。由此可见:提高外骨骼膝关节的驱动能力或降低膝关节的负载,能更大程度地减小负载对穿戴者的作用力,进而保护人体下肢较为脆弱的膝关节,更有效地降低外骨骼能耗。
笔者根据人体构造设计出单兵装甲下肢外骨骼简易结构,分析自由度驱动分配方案,运用零力矩点(Zero Moment Point)稳定判据进行外骨骼步态稳定控制[7],利用CAD软件Solidworks和动力学仿真软件ADAMS对外骨骼步态周期进行运动学和动力学仿真,验证设计的合理性,并对不同抬腿高度H下膝关节力矩曲线进行分析,以期通过合理配置各关节驱动力和改变穿戴者行走步态达到降低外骨骼能耗的目的。
1 人体行走步态及驱动分析
由于下肢外骨骼需要与人同幅度动作行走,因此对下肢外骨骼的研究必须从研究人的步态开始。
1.1 步态周期
步态指的是人在行走过程中肢体的协调关系[8]。人正常行走的过程通常发生在矢状面,图1以5连杆模型表示一个完整的步态周期[9]。

图1 人体下肢步态周期
这里以左脚为参考脚,从左脚尖离开地面开始,到左脚尖再次离开地面结束为一个完整的步态周期。整个步态周期可分为摆动相(swing phase)和支撑相(stance phase),其中:左脚从脚尖离开地面到脚跟接触地面为摆动相,约占步态周期的40%;左脚从脚跟接触地面到脚尖离开地面为支撑相,约占步态周期的60%。此外,根据两条腿相互之间的姿态,整个步态周期又可以分为单脚支撑期和双脚支撑期。
1.2 自由度及驱动分析
人体下肢运动主要依靠髋关节、膝关节和踝关节,双腿共有12个自由度。髋关节是一个典型的球窝关节,具有伸/屈、内收/外展和旋内/旋外3个自由度;膝关节是一个髁状关节,能进行前屈运动和小范围的转动,通常忽视膝关节旋转自由度,将其视为具有1个前屈自由度;踝关节活动范围较小,通常具有伸/屈和内收/外展2个自由度。在考虑可操作性的同时,应使外骨骼机器人尽量模拟人体下肢自由度的分配,在髋关节和膝关节设置驱动,以使大腿和小腿实现抬起并迈步。临床步态分析(Clinical Gait Analysis, CGA)研究提供的数据表明:人类在行走、下蹲、登台阶和大多数运动中,髋关节、膝关节和踝关节在矢状面释放大部分力量。因此,笔者采取了髋、膝、踝关节伸/屈自由度的主动驱动方案,由于所需驱动力矩较大,因此笔者采用液压驱动元件。另外,髋关节的内收/外展自由度提供侧向平衡力,所需驱动力矩较小,但对安装空间要求较高,液压驱动元件很难安装,因此笔者采用伺服电机驱动。考虑到节能,由于髋关节、踝关节的旋转自由度以及踝关节的内收/外展自由度耗能很小,无需驱动力矩,因此将其设计成被动关节,由使用者的相应关节带动[10]。
2 步态稳定控制及规划
人穿着下肢外骨骼机器人行走时必须要满足一个条件,即保持足底与地面接触;同时,需要规划能满足这一条件的外骨骼机器人的运动。为保证双足步行时的稳定性,笔者采用ZMP稳定判据,其主要思想是:双足步行时身体保持平衡,保证所承受的所有外力之合力的作用线通过支撑足,并且处于支撑足和地面接触的区域内[7]。因此,外骨骼ZMP应处于足底支撑多边形内[11],如图2所示,在单脚支撑阶段,支撑多边形是单脚触地的底面;在双脚支撑阶段,支撑多边形是双脚触地所形成的多边形。

图2 支撑多边形
2.1 稳定裕度
稳定裕度是指ZMP与支撑多边形边界的最小距离。人在穿着下肢外骨骼机器人行走时,稳定裕度决定其稳定性。当ZMP距支撑多边形的中心越近,则稳定裕度越大,行走也越稳定。在外骨骼能够快速响应人动作的前提下,人体可以主动调节重心,使ZMP在动态步行过程中始终保持在支撑多边形内[7]。
2.2 ZMP计算
由于穿戴者与外骨骼之间的交互,当ZMP处于多边形内时需要有足够的稳定裕度。根据动力学理论和算法,可以根据运动计算ZMP[11-12]。
地面作用力绕原点力矩为
τ=p×f+τp,
(1)
式中:p为ZMP位置坐标;f为地面作用力;τp为绕过ZMP的铅垂轴力矩。
地面作用力与动量、地面作用力力矩与角动量之间关系分别为

(2)

(3)
式中: P=(Px, Py, Pz)为总动量,Px、Py、Pz分别为P在各轴上的分量;M为总动量;g=(0, 0, -gz)为重力加速度,gz为g在z轴上的分量;L=(Lx,Ly,Lz)为角动量,Lx、Ly、Lz分别为L在各轴上的分量;c=(x,y,z)为质心位置坐标。
将式(1)、(2)代入式(3)可得

(4)
由于绕ZMP力矩的x、y两分量为0,可得

(5)
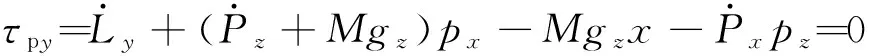
(6)
可从式(5)、(6)得到ZMP位置

(7)

(8)
假设人在平地上行走,则pz=0,因此,可得px和py分别为
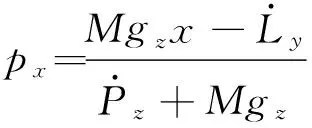
(9)
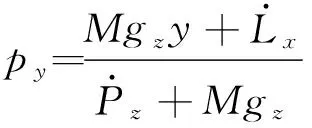
(10)
如果将机器人简化为一个质点,则




(11)

(12)
2.3 步态规划
根据外骨骼机器人行走时应满足的约束条件规划出踝关节轨迹,通过运动学逆运算得出相应关节角的时间函数。利用ZMP稳定判据得出外骨骼机器人行走ZMP轨迹,并求出在满足ZMP轨迹时稳定裕度最大的质心和摆动踝关节轨迹[13]。步态规划算法流程如图3所示。
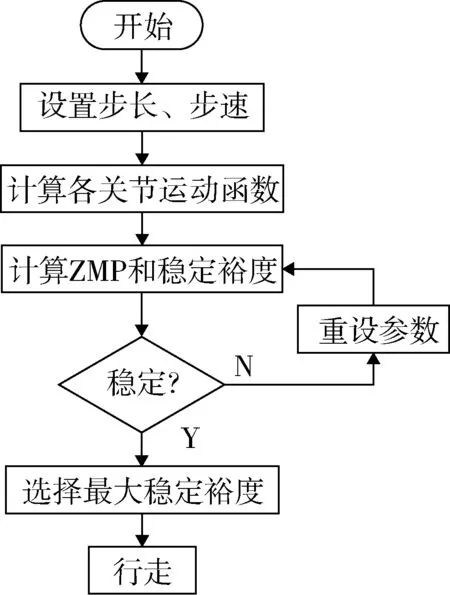
图3 步态规划算法流程
3 虚拟样机建模及仿真
3.1 外骨骼建模
本设计中单兵装甲下肢外骨骼机器人模拟人体的结构,可直接对外骨骼进行ZMP动态稳定性分析。对于复杂的机械结构,单纯依靠数学方法进行建模分析十分复杂,在实践中不可行,因此,笔者利用虚拟样机ADAMS对机械结构进行建模和仿真。为提高效率,利用Solidworks进行外骨骼机构建模,再通过数据接口导入ADAMS。模型导入后,对模型各关节添加约束和相应驱动力,进行运动学仿真[8]。这里,采用STEP函数实现对起步、左脚、双脚支撑期运动的控制。ISALEE单步行走仿真如图4所示。

图4 ISALEE单步行走仿真
笔者所在课题组在此基础上设计制作了简易样机,并通过仿真曲线对其运动性和灵活性进行了测试。图5为穿着样机时的平地行走灵活性测试。

图5 平地行走灵活性测试
3.2 仿真及分析
根据GB10000—1988给出的人体主要尺寸数据,以身高1 775 mm的成年男性为例,设置大腿连杆505 mm,小腿连杆403 mm。仿真仅在矢状面内进行,仅保留髋关节与膝关节的伸/屈自由度,采用旋转副连接,足部板视其为连接固定在小腿末端的质量块。通过在motion中添加STEP函数近似拟合外骨骼髋关节和膝关节的运动角变化曲线,实现对关节运动的控制。在仿真过程中,设定仿真步长200步,仿真时间3.5 s。图4中基于ZMP稳定控制判据对外骨骼机器人虚拟样机进行步态规划,样机右腿能够在半个步态周期内稳定前行,表明步态规划合理、控制方法有效。在后处理模块Postprocessor中,可对各约束上的数据曲线进行分析,这里以髋关节为例。
图6-8分别为半个行走周期内右髋关节的角度、角速度和转动力矩变化曲线。对其进行分析,可得以下结论:
1) 模型自然站立时,髋关节角度为0°,在半个步态周期内髋关节矢状面屈伸角度变化范围为0°~45° ,与控制函数设定相吻合;
2) 角度变化曲线平滑,没有尖点,且没有多余的起伏变化,说明外骨骼行走是一个平稳过程,验证了模型的有效性;
3) 角速度变化曲线在1.5、2.0 s处出现拐点,但波动不大,且通过拐点时外骨骼结构未发生变化,验证了运动稳定性;
4) 由于仿真周期为右腿摆动期,因此右髋关节力矩仅为正,其曲线绝对峰值为348 N·m,出现在右足落下与地面刚接触的时刻,可依此选择液压缸型号及液压泵大小,以满足驱动力设计要求。

图6 右髋关节角度变化曲线

图7 右髋关节角速度变化曲线

图8 右髋关节转动力矩变化曲线
图9为外骨骼髋关节屈向旋转角度不同,即大腿连杆抬腿高度H(在矢状面内,以髋关节为圆点,以大腿连杆长度为半径,以大腿连杆垂直于地面的位置为起始位置,当大腿连杆绕髋关节逆时针运动时,膝关节距地面高度即为H)不同的情况下膝关节转动力矩变化曲线,其中H1 图9 不同H下膝关节转动力矩变化曲线 本文对单兵装甲下肢外骨骼的结构进行了设计,对下肢外骨骼的步态进行了规划,通过ADAMS建立了虚拟样机并进行了仿真分析,结果表明:在合理设计机械结构以确保模型有效和运动稳定的基础上,提高外骨骼大腿连杆抬腿高度H可降低膝关节转动力矩,从而保护人体膝关节并更大程度地降低外骨骼能耗。 下肢外骨骼是一个复杂的非线性多体模型,笔者只是对人体进行简化而得到近似模型,研究结果仅限于下肢外骨骼在平地上的矢状面运动,后续将通过空间运动学分析和仿真进一步对下肢外骨骼的结构设计和能耗进行研究。 [1] 唐志勇,谭振中,裴忠才.下肢外骨骼机器人动力学分析与设计[J].系统仿真学报, 2013, 25(6): 1338-1344. [2] 李会营,王惠源,张鹏军,等.外骨骼装备在未来单兵系统中的应用前景[J].机械设计与制造, 2012(3): 275-276. [3] 韩亚丽,王兴松.行走助力机器人研究综述[J].机床与液压, 2008, 36(2):165-169. [4] 赵彦峻,徐诚,张景柱,等.人体下肢外骨骼关键技术分析与研究[J]. 机械设计, 2008, 25(10): 1-4. [5] 柯显信,陈玉亮,唐文彬.人体下肢外骨骼的发展及关键技术[J]. 机器人技术与应用, 2009(6): 28-32. [6] Grifn T M,Roberts T J,Kram R.Metabolic Cost of Generating Muscular Force in Human Walking: Insights from Load Carrying and Speed Experiments[J].J Appl Physiol,2003,95:172-183. [7] 易嘉伟,程文明,濮德璋.携行式外骨骼下肢运动学分析与仿真[J].机械设计与制造, 2014(2): 172-174. [8] 赵彦峻,徐诚.人体下肢外骨骼设计与仿真分析[J].系统仿真学报,2008,20(17): 4756-4759. [9] 张学胜,赖庆仁,陈亚宁,等.负重外骨骼机器人的设计及其运动学动力学仿真[J].机械科学与技术, 2013, 32(4): 568-572. [10] Chu A, Kazerooni H, Zoss A. On the Biomimetic Design of the Berkeley Lower Extremity Exoskeleton[C]∥Proceeding of 2005 IEEE International Conference on Robotics and Automation. Spain: IEEE, 2005: 4345- 4352. [11] 梶田秀司.仿人机器人[M]. 北京: 清华大学出版社, 2008. [12] 陈占伏,杨秀霞,顾文锦.下肢外骨骼机械结构分析与设计[J].计算机仿真, 2008, 25(8): 238-241. [13] 梁青,宋宪玺,周烽,等.基于ADAMS 的双足机器人建模与仿真[J].计算机仿真, 2010, 27(5): 162-165. [14] Huang Q, Yokoi K, Kajita S, et al. Planning Walking Patterns for a Biped Robot[J].IEEE Transactions on Robotics and Automation, 2001, 17(3): 280-289. (责任编辑: 尚彩娟) Design and Simulation Analysis of Individual Soldier Armored Lower Extremity Exoskeleton CHAO Zhi-qiang1, WANG Fei1,2, ZHANG Chuan-qing1, HAN Shou-song1 (1. Department of Mechanical Engineering, Academy of Armored Force Engineering, Beijing 100072, China;2. Troop No.66336 of PLA, Gaobeidian 074000, China) An Individual Soldier Armored Lower Extremity Exoskeleton (ISALEE) is designed for military, which takes advantages of human and machine to improve carrying capacity of soldiers during missions. The human lower extremity’s gait and degrees of freedom are analyzed with 5-links model. According to Zero Moment Point (ZMP) stability criterion, ISALEE’s dynamic stability is analyzed, and its gait is planned. Finally, the modeling and simulation of ISALEE virtual prototype are performed with CAD software Solidworks and dynamic simulation software ADAMS. The simulation result shows that structure design of the exoskeleton is reasonable with ADAMS virtual prototype, which provides theoretical basis for selecting hydraulic drive components and reducing load of knee. lower extremity exoskeleton; Zero Moment Point (ZMP); gait planning; simulation 1672-1497(2015)06-0053-05 2015-09-21 晁智强(1967-),男,教授,博士。 TP242.6 A 10.3969/j.issn.1672-1497.2015.06.011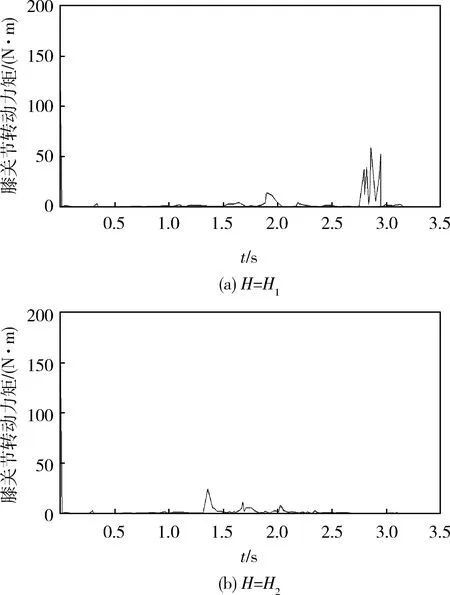
4 结论
