基于作战效能预测的坦克分队火力部署方法
2015-06-12陈军伟常天庆马殿哲
陈军伟, 常天庆, 马殿哲, 朱 祺, 张 林
(1. 装甲兵工程学院控制工程系, 北京 100072; 2. 北京特种车辆研究所, 北京 100072;3. 工程兵学院工程装备管理与保障系, 江苏 徐州 221004)
基于作战效能预测的坦克分队火力部署方法
陈军伟1, 常天庆1, 马殿哲2, 朱 祺2, 张 林3
(1. 装甲兵工程学院控制工程系, 北京 100072; 2. 北京特种车辆研究所, 北京 100072;3. 工程兵学院工程装备管理与保障系, 江苏 徐州 221004)
针对坦克分队的作战特点,对其火力部署方法、内容进行了分析,建立了一种基于排队论的坦克分队作战效能预测模型,给出了该模型中系统损失概率PM的求解方法,对不同作战态势下2种典型排队模型的作战效能进行了仿真计算。结果表明:通过求解模型可预测不同火力部署方法的作战效能,实现了基于作战效能的火力部署预测。
坦克分队;作战效能预测;火力部署
坦克分队火力部署方法主要研究指挥员如何根据敌我双方所处态势,合理确定坦克分队配属的武器类型、数量和打击敌人时所使用的战斗队形,是坦克分队火力优化技术的重要研究内容[1]。目前,有关坦克分队火力部署方法的文献报道很少。我军坦克分队指挥员仍主要依靠经验判断进行火力部署,因此,迫切需要研究一种科学有效的火力部署方法,以克服经验判断法的缺点,完善坦克分队火力优化技术。
合理进行坦克分队火力部署的关键是建立一种面向火力部署的作战效能预测模型,然后根据模型求解结果判断火力部署的优劣,进而实现基于作战效能预测的火力部署。羊彦等[2]基于整数规划预测了对空导弹协同防御模式的作战效能,但其模型的实时性不高。贺平等[3]采用Monte-Carlo法对多层、多级导弹防御体系的作战效能进行了预测,但其需要大量演算才能得到较精确的结果。曹雷等[4]基于爱尔兰排队系统理论构建了多级和协同防御模式下的作战效能预测模型,并比较了2种典型排队模型的作战效能,但其模型未考虑作战中存在的对抗性因素。
笔者针对坦克分队作战特点,基于排队论建立了一种作战效能预测模型,为坦克分队实现基于作战效能预测的战前火力部署提供了理论参考。
1 坦克分队火力部署分析
1.1 坦克分队火力部署的主要任务
由于战前分队级指挥员难以改变其配属的武器类型、数量和构成,因此,分队指挥员最重要的火力部署任务就是在战前的较短时间内确定运用何种战斗队形迎击敌人。坦克分队常用的战斗队形有一字队形、三角队形和梯形队形3种[5],其中:一字队形便于发挥火力和首次打击力量,但打击纵深较差;三角队形与梯形队形便于相互掩护,保护两翼或一翼安全,可形成对敌多轮次打击,但削弱了单次打击力量。
1.2 坦克分队战斗队形部署的影响因素
影响坦克分队战斗队形部署的因素主要分为5类:分队在上级部队队形中所处地位、作战环境、分队作战能力、敌方态势和后勤保障能力。其中:分队在上级部队队形中所处地位可直接决定战斗队形的部署,如分队位于上级队形编制内部时,两翼安全有保障,一般采用一字战斗队形迎击敌人;位于上级队形编制两翼的分队采用梯形战斗队形迎击敌人,以便保护侧翼安全。作战环境有时也可直接决定战斗队形的部署,如:在谷底、狭路进攻时,由于展开地域面积有限,只能采用三角战斗队形对敌打击。
在信息化条件下的现代战争,坦克分队更多地承担了独立作战的使命。此时,如果作战环境允许,战斗队形部署需要更多地考虑可能实现的作战效能。坦克分队火力部署影响因素及其评价指标如图1所示。

图1 坦克分队火力部署影响因素及其评价指标
2 基于排队论的作战效能预测模型
2.1 评价指标的抽象与量化
设作战背景为敌我双方处于交战前的某一时刻,坦克分队可获得所属武器装备的各项技术状况,上级指挥机构侦察到敌人数量、分布、武器类型等信息,并已将信息下发到坦克分队。
2.1.1 敌方态势
战前,分队指挥员根据上级敌情通报和分队发现的信息,结合作战环境进行敌方态势判断。判断主要围绕敌人的兵力数量、种类、作战能力、部署情况展开,目的是获取敌方具有最大战场价值的武器、某一时间段内可能发现的目标数量等战斗信息,为战斗部署提供依据。对上述因素的抽象量化包括如下3个方面。
1) 目标数量、种类和战场价值。设敌方共有k类m个目标,构成目标集T={Ti,i=0,1,2,…,m}。交火前可认为同一类目标的战场价值相同,令第l类目标的战场价值为vl(l=1,2,…,k),并规定v1>v2>…>vk。
2) 目标被发现的概率。在坦克分队杀伤区域内,某个目标被发现的概率服从参数为λ的泊松分布,由于k类目标被发现的概率相互独立,因此每类目标被发现的概率仍服从参数分别为λ1,λ2,…,λk的泊松分布,且λ=λ1+λ2+…+λk。则t时刻有x个目标被发现的概率为
(1)
式中:Xt为时刻t在杀伤区目标被发现的随机数;λ为单位时间(本文取1 s)内发现的目标数量。事件Xt=λ发生的概率最大,则当Xt≠λ时发生的概率都会减小。显然λ与目标密度、机动能力以及隐蔽情况相关。
3) 目标待射击时间。若目标被发现时,所有武器均处于射击状态,则目标选择等待射击。武器完成射击并获得射击该目标命令后,射击等待目标。等待射击的目标可能会在这一段时间内逃离或隐藏,分队将失去射击目标的机会。目标的射击等待时间服从参数为γ的负指数分布,其概率密度函数为
(2)
式中:tw为目标等待时间的随机数;γ为目标平均等待时间的倒数。实践中,对某个事件发生所需的等待时间往往被看作近似服从负指数分布。
另外,如果存在多个目标等待射击时,应首先射击战场价值较大的目标,令λm为等待射击目标中战场价值最大的目标单位时间内被发现的数量。
2.1.2 己方作战能力
战前,分队指挥员根据平时掌握的情况,结合各武器平台上报的状态信息,判断己方作战能力。主要内容包括武器数量、火力、存活能力等各项技术状况,目的是掌握火力情况、防御能力、机动能力,为作战部署提供依据。对上述因素的抽象量化包括如下3个方面。
1) 武器数量和射击时间。设己方有n个火力单元参与射击,构成武器集W={Wj,j=0,1,2,…,n}。武器在完成一次射击后立刻观察结果,指挥员根据打击效果安排武器继续射击该目标或是转火射击其他目标。射击一个目标所用的时间服从参数为μ的负指数分布,其概率密度函数为
(3)
式中:ts为武器射击一个目标所用的随机时间;μ=1/tf,其中tf为打击一个目标的平均射击时间。武器射击时间的分布函数在平均射击时间时概率最大,射击时间不等于平均射击时间的概率都会减小。
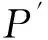

3) 武器生存能力。设处于前方梯队的武器在战场上存活的时间tl服从参数为α1的负指数分布,后方梯队武器战场存活时间服从参数为α2的负指数分布,α1、α2均为平均存活时间的倒数。
2.1.3 后勤保障能力和作战环境
设武器受损后立刻进行战场抢修,抢修一个受损武器所花费的时间tr服从参数为θ的负指数分布,θ为平均抢修时间的倒数。己方弹药、油料补给充足,作战环境对战斗队形的部署没有特殊影响,己方掌握制信息权,可获取战斗双方的态势信息。
以上对指标的抽象和量化体现了影响战斗队形部署的全部因素,能够反映坦克分队作战实际情况,且λk、μ、γ、α、θ等参数均可通过可行的计算方法获得[6-8]。
2.2 模型构建
根据Ⅱ级因素评价指标的抽象、量化及排队论[9],可将作战过程抽象为随机服务系统[10]:己方坦克车辆为服务台,打击的敌方目标为顾客,提供的服务为射击;则敌方目标被发现的概率即顾客到达排队系统的概率,己方坦克的射击时间即服务台的服务时间,目标待射击的时间即顾客排队等待的时间;改变迎敌时所采用的作战队形即对这个排队系统的服务规则进行控制,使其收获的作战效能最大。
采用不同的队形组织战斗队进行战斗,可构建不同服务规则的排队系统:侧重火力强度的一字战斗队形可抽象为如图2所示的排队模型(模型A);侧重防御纵深的三角队形可抽象为如图3所示的排队模型(模型B)。由图2、3可以看出:一字战斗队形和三角队形所构成的排队系统分别为1级并行排队系统和2级串、并混合排队系统。梯形战斗队形也可采用这种方法抽象为排队模型,不同的是其所构成的模型服务级数不同,同级中战斗队的数量也不同。考虑到构建方法相同,本文仅对最典型的一字和三角战斗队形所构成的排队模型进行分析。

图2 一字队形坦克分队对目标的射击过程
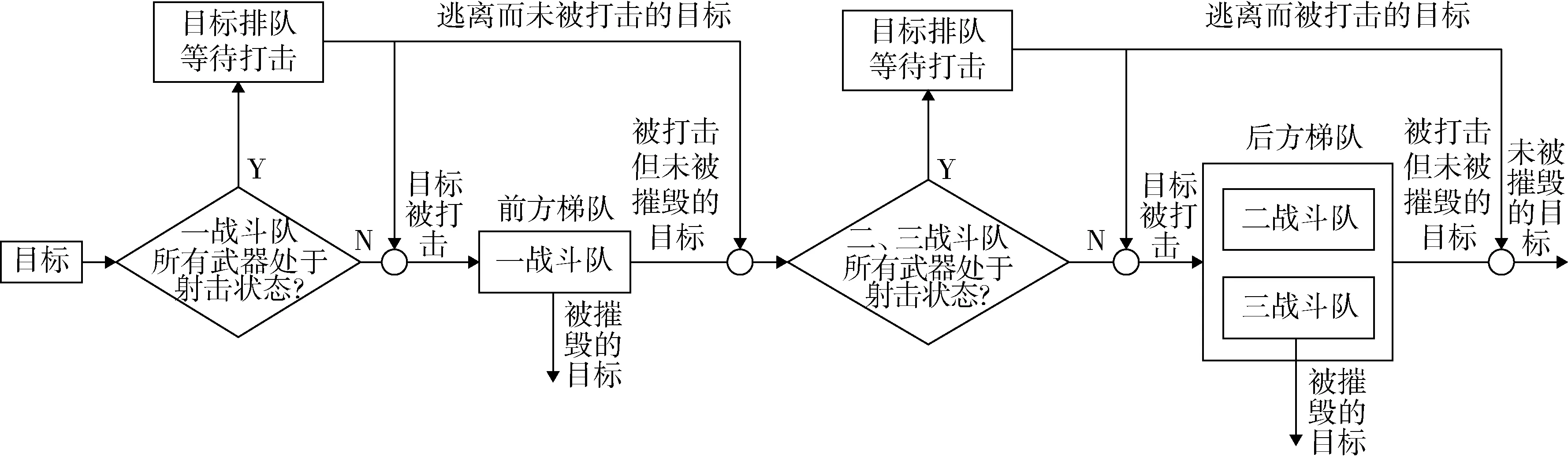
图3 三角队形坦克分队对目标的射击过程
将敌方坦克未被摧毁的概率PT作为作战效能预测指标。PT越低,则坦克分队作战效能越高;反之,坦克分队作战效能越低。由全概率公式可知:模型A中敌坦克未被摧毁的概率为
PTA=PMA+(1-PMA)(1-PkA)3;
(4)
模型B中敌坦克未被摧毁的概率为
PTB= [PMB1+(1-PMB1)(1-PkB)]×
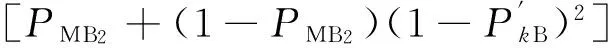
(5)

由基本假设可知:模型A是1级并行服务系统,模型B是2级串、并混合服务系统,二者同时又都是具有非强占型优先权、服务台故障率确定的混合延迟消失制M/M/N可修排队系统[11](简称“排队系统”)。在排队论中,PMA为模型A的系统损失概率,PMB1、PMB2分别为模型B第1级与第2级的系统损失概率。PMA、PMB1、PMB2的求解方法完全相同,因此研究该类排队系统损失概率PM的求解方法即可。
3 排队系统分析
令X(t)为时刻t出现的目标数量,Y(t)为时刻t可用于打击的有效武器,则随机过程{(X(t),Y(t);t≥0}描述了系统在时刻t的瞬时状态。设Pi,j(t)=P{X(t)=i,Y(t)=j,i=0,1,2,…,m;j=0,1,2,…,n},为系统在时刻t的瞬时状态,
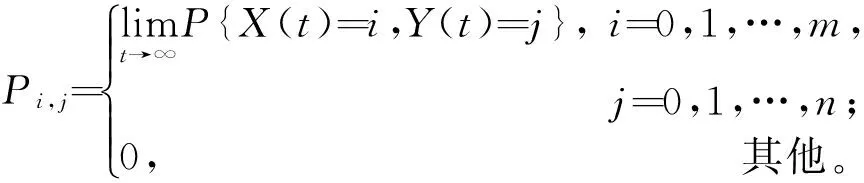
由于目标出现概率服从泊松分布,射击时间、武
器生存时间、战场抢修时间服从负指数分布,因此这一随机过程为状态空间Ω={(i,j),i≥0,j=1,2,…,n}上的二维马尔可夫过程。
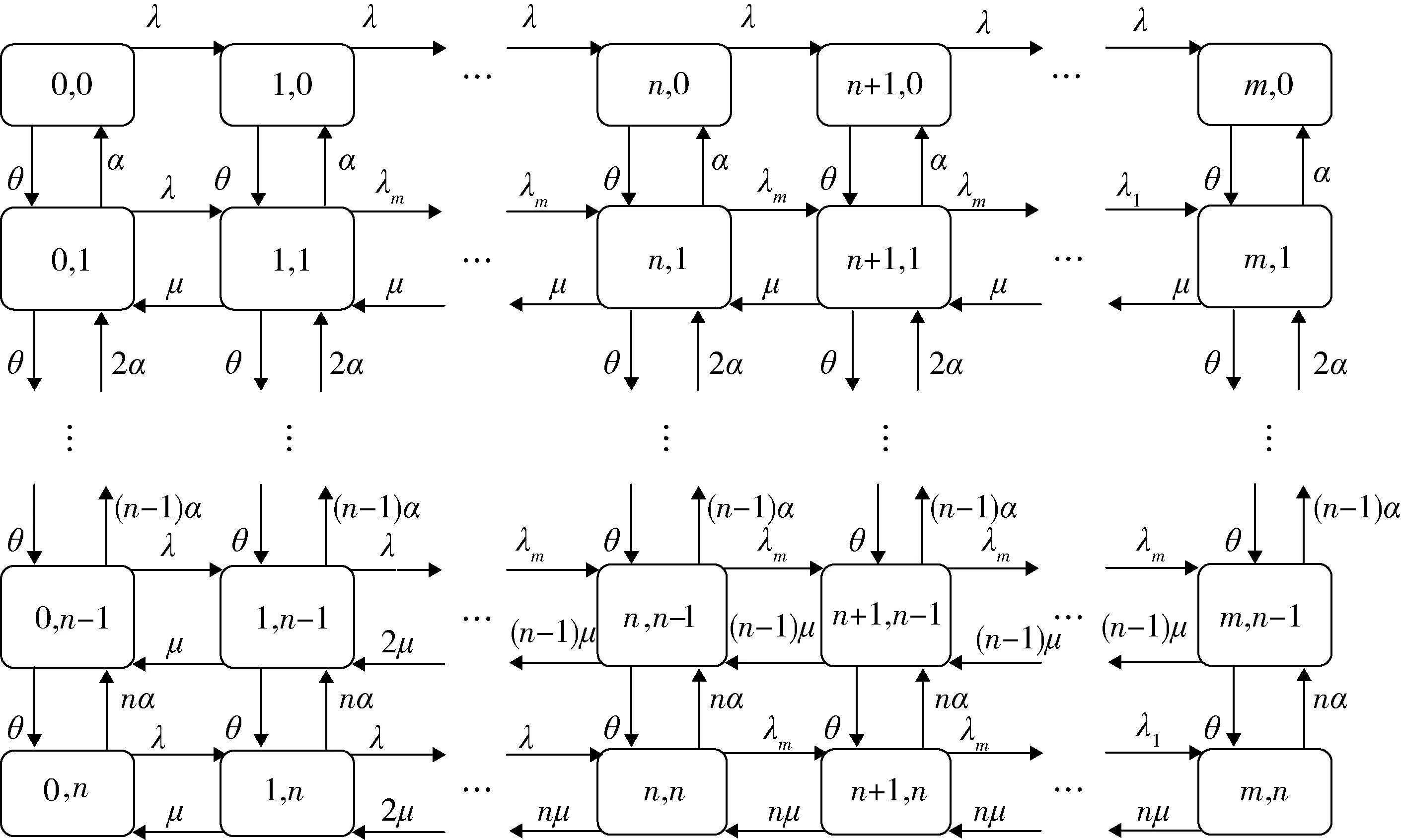
图4 排队系统状态转移图
根据图4,可得随机过程{X(t),Y(t);t≥0}的生成元矩阵Q,即
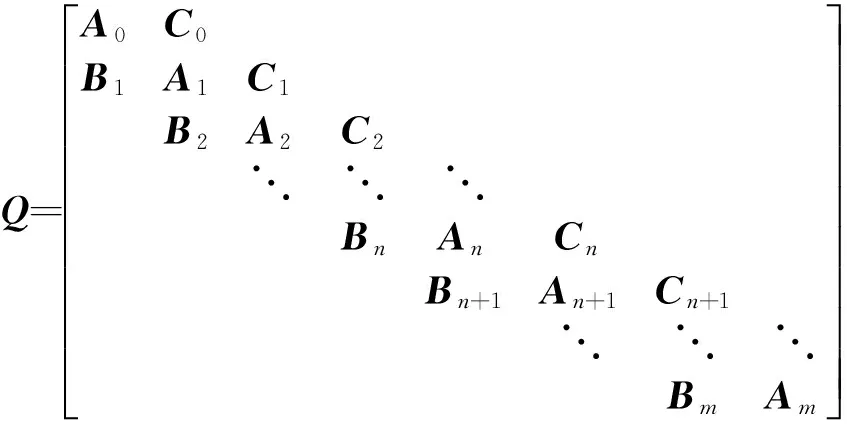
(6)
Q的每个分块都是n+1阶方阵,设I为n+1阶单位阵,则可得

(7)
式(7)中,当i=0时,
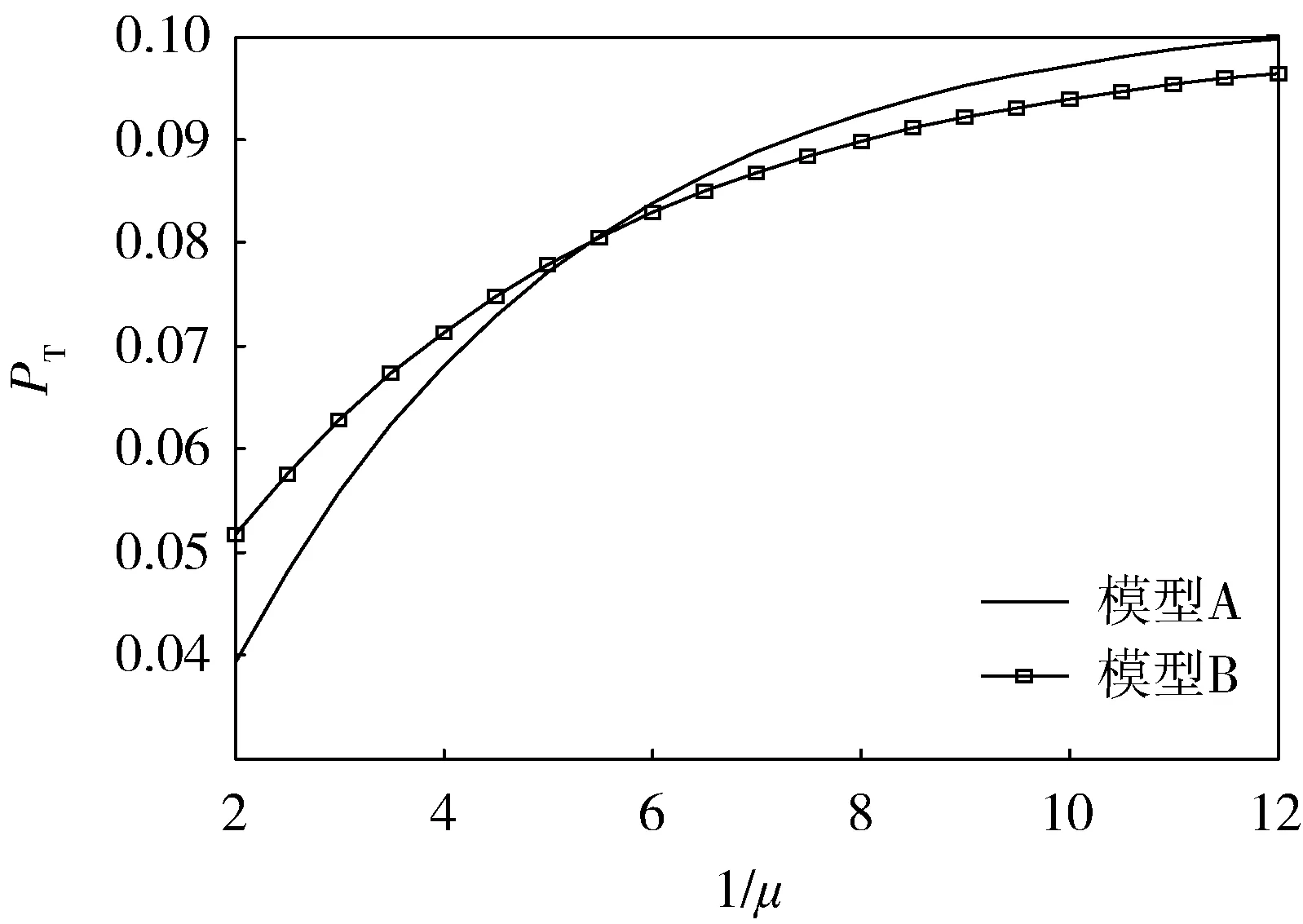
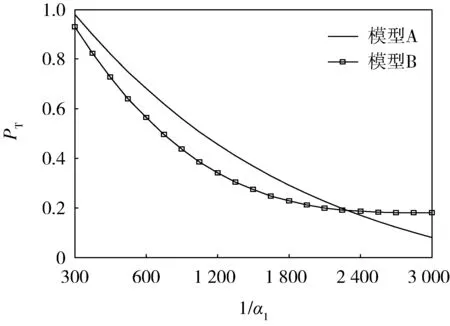
当0 当n A=An; Bi=diag(min(i,j)μ,0≤j≤n); B=Bn=diag(0,μ, 2μ, …,nμ); C0=C1=…=Cn=C=λI。 由于二维马尔可夫过程的生成元可写成分块三对角形式,故该过程是一个拟生灭过程[12]。这一拟生灭过程具有如下性质:矩阵方程R2B+RA+C=0的最小非负解R的谱半径sp(R)<1,且线性方程组P0(A0+RB1)=0有唯一正解。证明方法可参见文献[13]。因此,拟生灭过程存在稳态概率。通过状态转移图可得系统所满足的稳态平衡方程。 1) 当j=0时, 2) 当0 3) 当j=n时, (8) 4.1Gj(1)求解 由式(8)可看出求解系统损失概率可转化为求解Gj(1)。 对j取相同值的稳态平衡方程关于i求和,可得N+1个关于Gj(1),j=0,1,…,n的方程,具体为 (9) (10) 式(9)为n+1个相关的方程组,化简为n个独立的方程,再与式(10)组成关于Gj(1)的n+1个独立方程的方程组,具体为 (11) 4.2P0,j求解 对j取相同值的稳态平衡方程,两边同时乘以Zi+1,再对i求和可得n+1个关于Gj(z)的方程,即 (12) 利用文献[14]中的矩阵几何解法进行求解。为得到式(12)的矩阵形式,做如下规定: |A(z)|Gj(z)=|Aj(z)|,j=0,1,…,n。 (13) 求|A(z)|根的个数,首先做如下规定: 当0≤z≤∞时, (14) 可见:Qj(z),j=1,2,…,n是矩阵A(z)从第(n,n)个元素开始,反向沿主对角线取子矩阵的行列式。且存在如下递推关系: Qk+1(z)=fn-k(z)Qk(z)-(n-k+1)αθz2Qk-1(z)。 (15) 多项式Qk(z)具有如下性质。 1) Q0(z)在区间(0,∞)内没有根。 2) Qk(z)与Qk+1(z)在区间(0,∞)内没有任何公共根。 证明: 设z0>0是Qk(z)与Qk+1(z)的公共根,则由式(15)可知Qk-1(z0)=0;依据Qk-1(z0)=0,Qk(z0)=0以及式(15)可计算出Qk-2(z0)=0;最后递推得到Q0(z0)=0,这与性质1)矛盾。因此,Qk(z)与Qk+1(z)在区间(0,∞)内没有任何公共根,证毕。 3) 由式(14)可以看出:设z0是Qk(z)的正根,则Qk-1(z0)和Qk+1(z0)的符号相反。 4)Qk(z)>0;Qn+1(1)=|A(1)|=0。 证明: 将z=1代入式(14),可得 Q0(1)=1>0; Q1(1)=fn(1)=nα>0; Qk(1)=(n-k+1)(n-k+2)…(n-1)nα>0,2≤k≤n。 将Qn+1(z)=|A(z)|的各列求和后加到最后一行,提取产生的公因式(z-1),即 并记为 |A(z)|=(z-1)D(z), (16) 因此,Qk(z)>0;Qn+1(1)=|A(1)|=0,证毕。 5) Sign[Qk(0)]=(-1)k,k=0,1,…,n; Qn+1(0)=0。其中Sign[x]为符号函数。 证明: 由fj(z), (0≤j≤n)的定义可知f0(0)=0, fk(0)<0,1≤k≤n,将fj(0)(j=0,1,…,n)分别代入式(15),由于Sign[Q0(0)]=1=(-1)0,Sign[Q1(0)]=-1=(-1)1,则可证明,Sign[Qk(0)]=(-1)k, k=0,1,…,n; Qn+1(0)=0,证毕。 6)Qk(z),k=0,1,…,n+1的最高次项为(-λz2)k,又因为(-λz2)k确定了Qk(∞)的正、负符号,因此Sign[Qk(∞)]=(-1)k, k=0,1,…,n+1。 由性质1)-6),可得如下定理。 证明: 根据性质4)-6)可得出:Q1(z)是关于变量z的最高次幂为2的多项式,且存在2个不同的实根z1,1和z1,2,其中z1,1在区间(0,1)内,z1,2在区间(1,∞)内。因为Q1(z)>0,由性质3)可知Q2(z1,1)<0, Q2(z1,2)<0,再根据性质4)-6)可知在区间(0,z1,1)、(z1,1,1)、(1,z1,2)、(z1,2,∞)内至少各包含Q2(z)的1个实根,又因为Q2(z)中z的最高次幂为4,因此最多有4个实根,所以区间(0,z1,1)、(z1,1,1)、(1,z1,2)、(z1,2,∞)中各包含Q2(z)的1个且仅有1个实根。进行n推导,可分析出Qn(z)中z的最高次幂为2n,因此最多有2n个不同实根,在区间(0,1)和(1,∞)内各有n个,令zn,j(j=1,2,…,2n)为这2n个根,且zn,1 Sign[Qn-1(zn,j)]=(-1)n+j, j=1,2,…,n; Sign[Qn-1(zn,j)]=(-1)n+j+1, j=n+1, n+2, …, 2n。 由性质3)可知: Sign[Qn+1(zn,j)]=(-1)n+j+1, j=1,2,…,n; Sign[Qn+1(zn,j)]= (-1)n+j, j=n+1, n+2, …, 2n。 由于Qn+1(z)关于z的最高次幂为2(n+1),因此最多有2(n+1)个实根,在zn,j(j=1,2,…,n)的相邻两点之间各有Qn+1(z)=|A(z)|的1个实根。同理,在zn,j(j=n+1, n+2, …, 2n)的两点之间各有|A(z)|的1个实根。这样就确定了|A(z)|的2(n-1)个实根。 至此|A(z)|的2(n+1)个实根全部被确定,且各不相同,其中有n-1个实根在区间(0,1)内。证毕。 设zk(k=1,2,…,n-1)为|A(z)|在区间(0,1)内的n-1个不同的实根。将z=zk代入式(12)得到|Aj(zk)|=0,k=1,2,…n-1,j=0,1,…,n。对每个zk均存在n+1个关于未知概率P0,j, j=1,2,…n的相关线性方程,可选择其中任意一个作为关于P0,j的方程,由区间(0,1)内的n-1个不同实根就可得到n-1个独立的关于P0,j的方程。 为得到最后一个独立方程,可将|A(z)|,j=0,1,…,n的第1行到第n行全加到最后1行,提出产生的公因式(z-1),可得: |Aj(z)|=(z-1)Dj(z)。 (17) 将式(16)、(17)代入式(13)可得: D(z)Gj(z)=Dj(z),j=0,1,…,n。 (18) 将z=1代入式(18)可得: D(1)Gj(1)=Dj(1),j=0,1,…,n。 (19) 根据前文,已知Gj(1)可由P0, j来表示,所以式(19)中的n+1个方程是相关的,可从中选择一个方程和前面的n-1个方程组成n个独立的关于P0, j的方程,从而解出P0, j、Gj(1)和PM。 为了不失一般性,仿真算例中参数都应采用随机方法生成,由于模型是对坦克分队作战过程的抽象,如果模型参数的选择过于偏离坦克分队作战实际,将失去数据分析的物理意义。因此首先对模型中的参数进行约定,算例中的参数将在约定的范围内随机产生,具体如表1所示。 表1 模型参数选取范围 5.1 坦克分队战斗队形部署方法 设定仿真实验的背景为敌我双方处于交战前某一时刻,作战环境对战斗队形部署无影响,己方可根据预期产生的作战效能进行战斗队形部署。模型中参数可在选取范围内随机产生。表2为从随机数据中选取的3组典型的战斗队形部署参数,每组参数都可体现1种作战态势。在3种不同作战态势下,采用一字战斗队形(模型A)和三角战斗队形(模型B)产生的作战效能指标PT及战斗队形决策结果如表3所示。 由表3可以看出:坦克分队战斗队形部署方法可在作战环境允许的情况下,通过预测不同战斗队形所能产生的作战效果,实现科学的战斗队形部署,辅助分队指挥员进行战斗决策。该方法也可分析战斗队形部署中参数对决策结果的影响。 表2 战斗队形部署参数 表3 采用不同战斗队形产生的作战效能指标PT 5.2 武器、目标数量对战斗队形部署的影响 表4 模型A/B的PT平均值 由表4可以看出:当m 为避免武器、目标数量对比这一因素掩盖其他因素对战斗队形部署的影响,在分析其他因素时,做如下假设:己方有3个战斗队共10个武器参与射击,敌方目标有4个种类共13个目标。 5.3 武器因素对坦克分队战斗队形部署的影响 图5 PT与1/μ的关系曲线 由图5可以看出:PT随1/μ的上升而升高,即射击反应时间越长,越可能导致无法摧毁敌人。比较2个模型发现:当射击反应时间较短时,采用一字战斗队形所产生的作战效能较高;反之,采用三角战斗队形所产生的作战效能较高。 图6 PT与1/α1的关系曲线 由图6可以看出:PT随1/α1的上升而下降,即武器生存时间越长,越不易出现无法摧毁敌目标的情况。比较2个模型发现:当武器平均生存时间较长时,采用一字战斗队形所产生的作战效能较高;反之,采用三角战斗队形所产生的作战效能较高。 图7 PT与PkA的关系曲线 由图7可以看出:PT随战斗队命中目标概率PkA的上升而下降,即命中概率越高,越不易出现无法摧毁敌目标的情况。比较2个模型发现:当毁伤概率PkA较小时,采用三角战斗队形产生的作战效能较高;反之,采用一字战斗队形产生的作战效能较高。 综合分析可以看出:μ、α、PkA同为反映武器性能的参数,一字战斗队形在武器性能优势明显时可获得更高的作战效能,而三角战斗队形则在武器性能优势不明显时获得更高的作战效能。即一字战斗队形更加有利于充分地发挥武器性能优势,而三角队形可以通过相互掩护来弥补武器性能的不足。 5.4 目标因素对坦克分队战斗队形部署的影响 除目标数量外,目标因素参数主要包括λ、vl和γ,通过实验发现vl对2种战斗队形作战效能的影响基本相同,因此,仅讨论其他因素的影响。 图8 PT与λ的关系曲线 由图8可以看出:PT随λ的上升而上升,即单位时间内可能发现的敌人数量越多,越容易出现无法摧毁敌目标的情况。比较2个模型发现:当单位时间内可能发现的敌人数量λ较小时,采用三角战斗队形产生的作战效能较高;反之,采用一字战斗队形产生的作战效能较高。 图9 PT与1/γ的关系曲线 由图9可以看出:PT随1/γ的上升而下降,即目标平均等待射击时间越长,越容易出现无法摧毁敌目标的情况。比较2个模型发现:当目标平均等待射击时间较短时,采用一字战斗队形产生的作战效能较高;反之,采用三角战斗队形产生的作战效能较高。 综合分析可看出:λ、γ是反映目标情况的参数,一字战斗队形更加适合应对敌人相对集中、机动隐蔽能力强的战场,三角战斗队形更加适合应对敌人分散的纵深战场。 通过上述分析可以看出:基于作战效能预测的战斗队形部署方法,既可在战前辅助分队指挥员进行队形部署决策,还可分析不同作战态势下各参数对战斗队形部署的影响。 本文通过建立一种基于排队论的作战效能预测模型,解决了坦克分队火力部署科学性不足和缺乏有效手段的问题。但本文对坦克作战中目标数量和战场抢修时间的假设过于理想化,下一步将在目标数量未知或受损坦克不能及时得到抢修的情况下对排队论模型非稳态解的渐近行为进行研究。 [1] 牛德智, 陈长兴, 班斐, 等. 基于效能评估的航空作战进程预测[J]. 航空学报, 2014, 35(5): 1416-1423. [2] 羊彦, 吴茜, 景占荣. 导弹防御系统协同拦截的有效性分析[J].系统工程学报, 2008, 23(2): 233-237. [3] 贺平, 吴钰飞, 罗小明. 基于Monte-Carlo模拟的多枚弹道导弹突防反导防御系统效能研究[J]. 装备指挥技术学院学报, 2007,18(4):53-56. [4] 曹雷, 董强, 彭伟, 等. 基于排队论的导弹防御系统的效能分析[J]. 南京理工大学学报, 2011, 35(4):470-474. [5] 郁志本.坦克兵战术学[M].北京:解放军出版社,2005:96-113. [6] 徐克虎,黄大山,张志勇,等. 坦克分队火力打击实际量化研究[J]. 火力与指挥控制, 2014, 39(8): 98-101. [7] 徐文超, 薛青, 张国辉, 等. 基于效能分析的坦克主动防护系统建模研究[J]. 火力与指挥控制, 2015, 40(4): 84-87. [8] 尤志峰, 石全, 雄飞. 基于加权支持向量回归的抢修时间估计模型[J]. 现代防御技术, 2014, 42(4): 160-166. [9] Vahid H, Vahid K, Madjid T. The Redundancy Queuing-location-allocation Problem: A Novel Approach [J]. IEEE Transactions on Engineering Management, 2014, 61(3):534-544. [10] Zhang H P, Yin B Q, Lu X N. Modeling and Analysis for Streaming Service Systems [J].International Journal of Automation and Computing, 2014, 11(4): 449-458. [11] Guha D, Pathak S S. Analysis and Performance Comparison of Uniform and Mixed Service Policy for Vacation Queue [EB/OL]. (2012-02-05) [2015-03-20]. http://ieeexplore.ieee.org/xpl/login [12] 王梓坤,杨向群. 生灭过程与马尔可夫链[M]. 北京: 科学出版社,2005:53-54. [13] Guo P C.The Newton-Shamanskii Method for Solving a Quadratic Matrix Equation Arising in Quasi-birth-death Problems[J].East Asian Journal on Applied Mathematics,2014,4(4):386-395. [14] 田乃硕, 岳德权. 拟生灭过程与矩阵几何解[M].北京: 科学出版社, 2002: 23-24. (责任编辑: 王生凤) Firepower Deployment Method of Tank Unit Based on Operational Effectiveness Prediction CHEN Jun-wei1, CHANG Tian-qing1, MA Dian-zhe2, ZHU Qi2, ZHANG Lin3 (1. Department of Control Engineering, Academy of Armored Force Engineering, Beijing 100072, China;2. Beijing Special Vehicle Research Institute, Beijing 100072, China;3. Department of Engineer Equipment Management and Support, Academy of Engineer, Xuzhou 221004, China) For the feature of tank unit, the method and contents of firepower deployment are analyzed. An operational effectiveness prediction model of tank unit based on queuing theory is established, a solution of the system loss probability valuePMin the model is proposed, and the operational effectiveness of two typical queuing models in different combat situation is simulated. The simulation results reveal that the model can calculate the operational effectiveness of different firepower deployment and the firepower deployment method based on operational effectiveness prediction is established. tank unit; operational effectiveness prediction; firepower deployment 1672-1497(2015)06-0014-11 2015-07-22 军队科研计划项目 陈军伟(1985-),男,博士研究生。 E917; TJ811 A 10.3969/j.issn.1672-1497.2015.06.004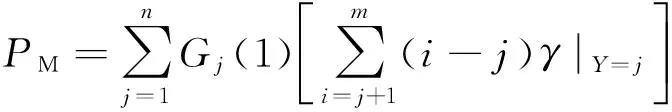
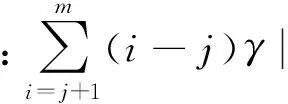
4 系统损失概率求解


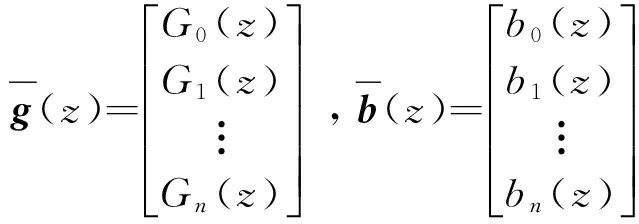
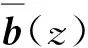


5 仿真计算





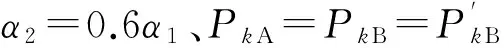
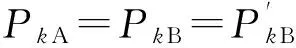

6 结论
