基于自适应遗传PID算法的溶解氧（DO）浓度控制

摘 要：曝气池溶解氧（DO）是一个重要的运行参数。采用自适应遗传PID算法实现溶解氧浓度控制具备在线调整功能，可以动态适应工况变化，取得良好的控制效果。

关键词：自适应;PID;DO

曝气池溶解氧（DO）在污水处理中是一个重要运行参数，理论分析，当溶解氧达到0.3mg/L就不会影响水中微生物的生理功能。考虑到水质及水量变化波动情况，通常保证入口处为0.5-1mg/L，出口处为2-3mg/L。按溶解氧数值控制风量是目前比较理想的控制方法。在城市生活污水停留时间内需要氧气（或空气）数量与污水的水质指标有关，如SS（悬浮物）、COD（化学需氧量）、BOD （生物需氧量）、水量及水温等。根据工艺理论分析，通过经验公式计算可以得到鼓风量的理论值。在实际运行时，能够根据进水的水质和水量的变化对鼓风量作出调整。实际工作中，需要通过实验得到污水水质指标。测定一些指示需很多时间，如测量COD需要数小时，测量BOD甚至需要几天时间，这不利于进行实时控制。实际工程应用中，对于连续流动的曝气池，只要污水在曝气池出口的溶解氧浓度保持在某一设定值，就可以不考虑水质、水量、水温等扰动的变化，从宏观上能较好地满足菌胶团繁殖和有机物分解的需要，从而保持污泥活性，保证污水的连续处理。为达到可靠的控制，可参数间的关系是：污水中溶解氧含量的偏差与曝气量的增量（或减量）成反比，即当溶解氧值偏小时，向大调节气量;反之亦然。当我们在实际中，曝气量值的设定是根据工艺理论值为参考的，经溶解氧反馈信号比较后，再根据偏差大小的结果随时对气量的多少进行调节，从而确保了污水的溶解氧值可以维持最初设定值内。下面是国内污水处理厂设计当中常采用的控制方案。

图1  溶解氧控制过程框图

如图1所示的串级控制系统，副回路采用PI控制策略，主回路一般采用PID控制策略。这样虽然比简单的单回路系统控制效果好，但是由于溶解氧控制过程是一个极其复杂的化学反应过程，非线性、大滞后。传统的PID参数整定方法很难确定合适的PID参数，并且参数不具备在線调整功能，无法适应工况变化，难以取得良好的控制效果，因此本文主要研究溶解氧浓度PID控制器参数自整定的方法进行研究。

1 溶解氧控制过程仿真模型的建立

要想对溶解氧浓度的控制过程进行研究，首先要建立其数学模型。活性污泥去污水处理系统是一个复杂的实时动态工程系统，没有精确的数学模型作具体表述。因此，在建立曝气过程动态仿真模型时，需要设定一些假设条件：第一种情况：曝气过程在时间上呈理想的推流变化，在空间上呈完全混合状态。第二种情况：在一个周期内，忽略合成的微生物量，假设反应池中总生物量近似不变。第三种情况：在一个周期开始前，忽略上一周期出水浓度。第四种情况：假设反应期的反应速率为一级，即假设既定的废水反应速率为常数。根据溶解氧浓度的物料平衡算式：

溶解氧DO浓度变化率=DO输入率-DO输出率-DO消耗率，我们建立的曝气过程动态数学模型如下：

V=Q·C0-Q·CI-V·k·C（1）

其中，C为反应池中的溶解氧浓度;Q为空气流量;V为反应池容积; C0为鼓入空气的溶解氧浓度;k为反应速率常数;CI为尾气中的溶解氧浓度。

对上式通过拉普拉斯变换得：

G（s）===（2）

令（C0-CI）/V=R则式（2）变为G（s）=R·（S+k），是一个惯性环节。

通常采用隔膜电极法测量溶解氧浓度。根据DO分析仪的测定原理及电化学方程式有：

DONT=DOST+r/a=（1-e-ar）（3）

其中DONT为T时刻DO的实测值（单位mg/L）;DOST为T时刻水样中实际DO浓度值（单位mg/L）;a为DO仪氧电极响应参数（单位min）;r为微生物耗氧速度（单位mg/（l·min））。

可知对溶解氧的检测是非线性的，并在时间上具有滞后特性。我们对模型可以进行纠正，将检测滞后用来表示，则式（3）纠正为：

G（S）=R/（S+k）-e-τs（4）

上式是曝气过程的近似仿真模型。根据实验数据和经验分析，上式可近似认为是曝气过程的近似仿真模型。根据实验数据和经验，这里将模型中的取R为18.39;k取为0.0186;τ取为1.35。

2 基于遗传算法的溶解氧控制PID参数整定方法研究

在一个已知的PID调节控制系统中，我们要确定Kp，Ki，Kd这三个参数，用这3个参数来确定系统。采用遗传算法进行PID参数调节，就涉及在固定的范围内寻找最优秀的PID参数。这里采用遗传算法进行PID调节的系统结构图如下：

图2  遗传算法整定PID参数系统结构图

实现整定的步骤是：

①对参数实数编码并初始化种群。采用实数编码寻优的PID参数 Kp，Ki，Kd。设随机生成种群规模为40的初始群体，假设若系统中有M个参数需要优化，我们可将这此参数为分量构成一个M维行向量，并将其他作为个体编码，见下式P=[P1，P2，…，PM]（5）

上式中：P代表个体;在第i个参数的参数空间内随机产生的一个分量用Pi表示;所有待优化参数的数目用字母M表示。在本文中每个个体有三个分量Kp ，Ki， Kd，每个分量取值范围根据ZN方法整定的Kp，Ki，Kd做内核，可设参数Kp[KPmin，KPmax]、Ki[KImin，KImax]、Kd[Kdmin，Kdmax]。

②适应度函数调整。因为在遗传算法中，适应度完全取决于个体的优劣性，从而对遗传算法结果造成了一定的影响，所以结果质量的一个关键因素是目标函数的设计。在系统参数整定过程中，需要根据性能指标的不同来选择。

在不同的生产过程对系统指标要求不同，而这些指标又是用于评价PID参数的好坏，所以非常重要。单项性能指标只对局部特性进行衡量，难以全面反映系统的情况，所以IAE、ISE、IATE等误差积分性能指标也是我们要考虑的重要参数。采用误差绝对值时间积分性能指标作为参数选择的最小目标函数可以获取满意的过渡过程动态特性。

J=e（t）dt（6）

③进行选择操作。采用轮盘赌（roulette wheel）选择方式，此方式首先要计算个体的适应值，为了求出该个体在选择过程中被选中的概率，必须计算此适应值在群体总适应值中所占的比例。

④变异与交叉操作。本文利用式（2）、式（3）來分别计算出交叉、变异概率Pc，Pm。采用此种方法克服了常规根据经验选取交叉、变异参数造成未成熟收敛的缺点。

⑤终止条件。选取固定的迭代次数（一般M=100）。直到达到较满意的结果为止。

3 仿真试验及其结果分析

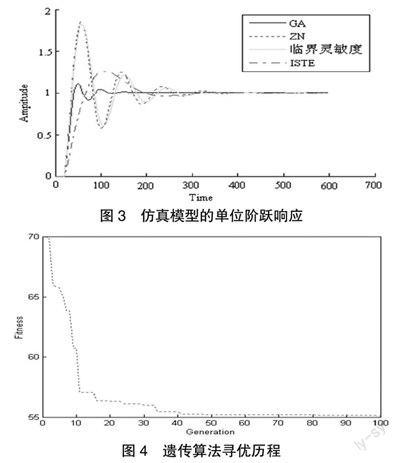
针对上述整定方法，本文应用前面建立的溶解氧过程模型对其进行仿真研究。我们首先用前面介绍的Ziegler-Nichols设定法、临界灵敏度法、ISTE最优设定方法对模型PID参数进行整定，然后选用遗传算法与它们对比。这里遗传算法种群数目均选为30，迭代次数选的是100次，交叉概率和变异概率按上述步骤中提到的公式进行计算得到。这里Kp，Ki，Kd 的取值范围为：Kp[0，4]，Ki[0，2]，Kd[0，1]。得到如图3所示的仿真曲线。

由上述仿真结果可以看出，采用遗传算法对PID的参数进行优化后，系统能较快的跟随设定值，而且超调明显减小，调节时间也有所缩短，使系统能在一个整体性能较好的条件下工作。要想将此PID整定算法应用到实际的控制过程中，必须编写遗传算法PID程序，由于控制现场的PLC不适合做复杂的运算，因此本文将此算法用WinCC监控软件的C脚本语言来实现，WinCC软件通过PLC采集控制系统误差根据文中算法计算出控制量后输出给PLC，PLC控制现场设备。仿真结果表明，该方法比传统的PID参数整定方法有明显的优势，能够应用到溶解氧的控制当中。

作者简介：王威（1982-），女，辽宁鞍山人，研究生，讲师研究方向：自动控制。