弯矩分配法在大型回转窑筒体设计中的应用*

张擎宇，赵冬博

(辽宁五寰科技发展有限公司，辽宁沈阳 )

0 引言

某公司年产10万吨镍铁项目，选用两条规格为φ4.8×110 m回转窑，采用4档支撑，属于国内大型回转窑，设计过程中其力学模型属于多跨连续梁的求解问题，由于模型中包含两个虚约束，因此无法通过静力平衡方程求解，属于二次超静定梁，对于此类问题可以采用三弯矩方程求解，但是步骤繁琐，计算量大。而采用弯矩分配法求解，不仅计算量小，而且步骤简单明了，效率高，是解决此类问题较为理想的方法。因此，采用弯矩分配法对φ4.8×110 m筒体设计中涉及到的跨距分配、筒体强度校核以及支反力计算等问题进行求解。

1 筒体所受载荷

筒体所受载荷主要包括:①筒体、耐火砖及物料重力产生的载荷，可视为均布载荷;②窑头护板、大齿圈以及挡料坝的重力产生的载荷，可视为集中载荷。

1.1 筒体载荷

筒体受载荷图情况如图1所示。

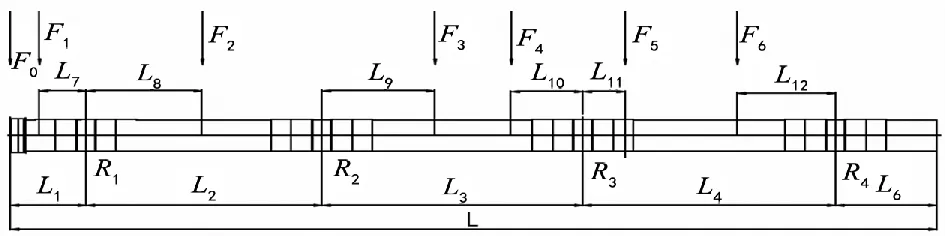
图1 筒体受载荷图

1.2 筒体载荷简化

利用材料力学方法，窑头窑尾悬伸段可分别简化为集中力P1、P4和等效弯矩M1、M4［2］，如图 2。

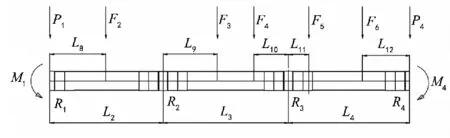
图2 筒体载荷简化图

1.3 筒体载荷具体数值

1.3.1 均布载荷

筒体内径:φ4.8 m，总长度:110 m。

综合考虑筒体自重、耐火砖重力及物料的重力，计算每跨的均布载荷

第一跨均布载荷:qt1=168.17 kN/m

第二跨均布载荷:qt2=167.13 kN/m

第三跨均布载荷:qt3=167.46 kN/m

窑头悬伸段均布载荷qt0=174.11 kN/m

窑尾悬伸段均布载荷qt4=169.95 kN/m

1.3.2 集中载荷

(1)窑头护板及冷风套重力

F0=70 kN

(2)挡料坝重力

F1=F2=F3=F4=F6=250 kN

(3)大齿圈装置重力

F5=400 kN

(4)根据材料力学计算集中力

P1=1 886.99 kN，P4=2 039.41 kN

1.3.3 等效弯矩

根据材料力学计算等效弯矩:

M1=8 767.97 kN·m，M4=11 598.33 kN·m

1.3.4 长度值

L2=28 m，L3=31 m，L4=30 m，L8=13 m，L9=13 m，L10=8 m，L11=5 m，L12=11 m

2 利用弯矩分配法对筒体进行分析计算

2.1 弯矩分配法的原理

弯矩分配法是根据叠加原理，将结构件的受载状态分解成一些简单状态(称为“固定状态”与“放松状态”)，这些简单状态的杆端弯矩(即支座截面弯矩)可查表按公式分别计算。将计算结果叠加，即求得受载状态下的杆端弯矩。

2.2 弯矩分配法的具体应用

结合本次计算，首先根据弯矩分配法，在第二档与第三档增加固定约束，图2可以转化、分解为三段梁，如图3。

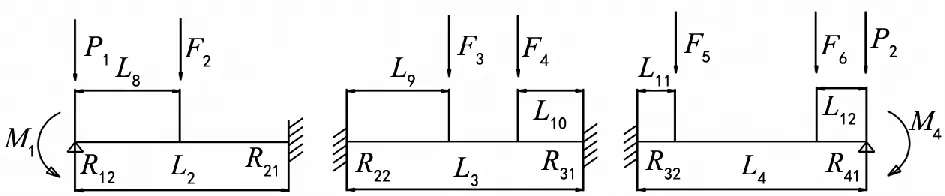
图3 固定端弯矩图

在此需要先阐述两个概念:

(1)杆端抗弯劲度KAB:在任意杆件AB中，使杆端A产生单位转角(顺时针为正)，而需在A端所加弯矩的绝对值，称为A端的抗弯劲度。

(2)杆端弯矩的传递系数CAB:在杆件AB中，使杆端A产生单位转角需要在A端加弯矩MAB，同时在B端产生弯矩MBA，称为传递弯矩。比值CAB=MBA/MAB，称为传递系数，此时的传递方向为A→B。两种基本杆件的 KABCAB值如图 4［1］:

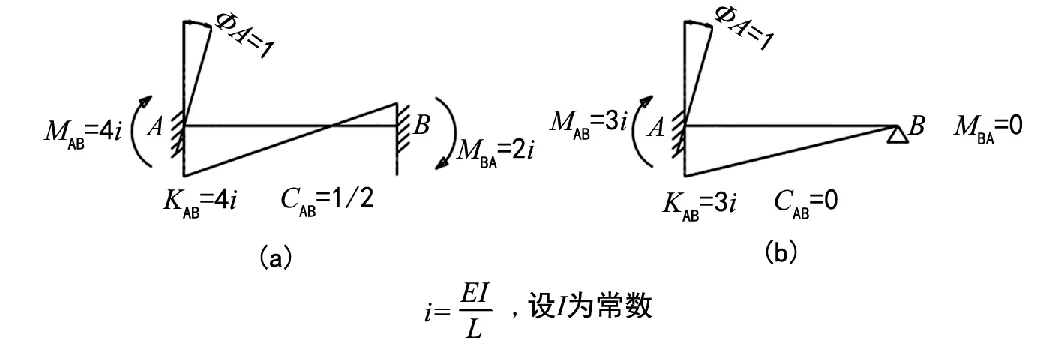
图4 弯矩分配法的基本杆件图

2.2.1 杆端抗弯劲度

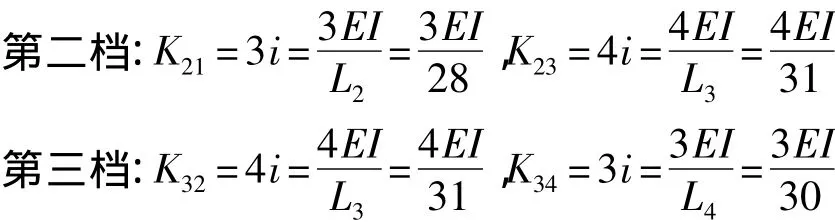
2.2.2 分配系数

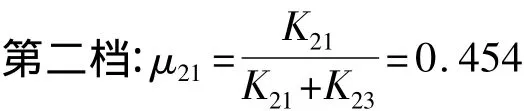
2.2.3 计算固定端弯矩

查表计算不同载荷在固定处产生的弯矩，并叠加得［3］:

第二档固定弯矩:

M21=13 371.21 kN·m，M23=14 863.24 kN·m

第二档固定弯矩:

M32=15 276.87 kN·m，M34=15 757.44 kN·m

2.2.4 传递系数

2.2.5 将固定弯矩按分配系数进行分配

分配图如图5所示。根据计算结果将连续梁分解为三段简支梁，如图6。

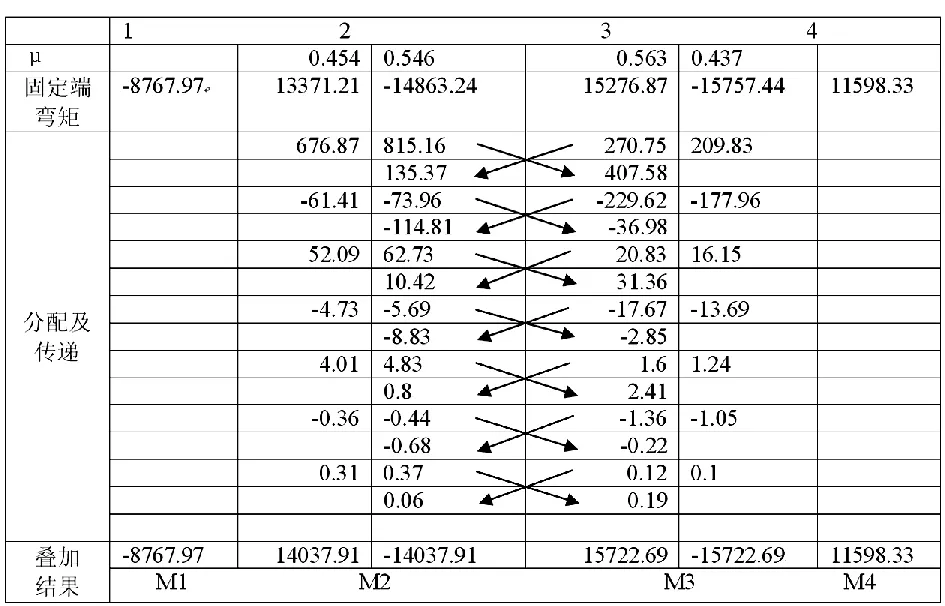
图5 分配图

图6 连续梁分解图

利用材料力学，分别求得支反力:

P1=1 886.99 kN，R12=2 300.07 kN

R21=2 658.64 kN，R22=2 745.89 kN

R31=2 935.23 kN，R32=3 074.03 kN

R41=2 599.35 kN，P2=2 039.41 kN

则各支撑档总支反力为:

R1=R12+P1=4 187.07 kN

R2=R21+R22=5404.53 kN

R3=R31+R32=6 009.54 kN

R4=R41+P2=4 638.76 kN

总支反力:

R=R1+R2+R3+R4=20 239.89 kN

总载荷:

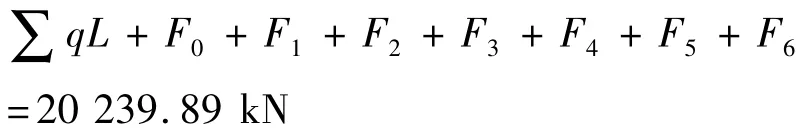
总支反力与总载荷相等。

3 校核危险截面的应力

应力计算选取危险截面进行:辊圈下支撑处，辊圈附近第一条焊缝处，跨间最大弯矩处。

筒体横截面上的弯矩应力为:

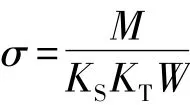
式中:KS为焊缝强度系数 (筒体采用自动焊，系数取值为0.95);KT为温度系数 (筒体工作温度不超过250度，系数取值为0.83);W为抗弯截面系数［1］。

3.1 跨间最大弯矩点

根据材料力学计算每跨最大弯矩点:

第一跨:X=13.68 m，第二跨:X=14.93 m，第三跨:X=15.97 m。

3.2 危险截面的抗弯截面系数

筒体的危险截面主要在:滚圈下支撑处、支撑附近焊缝处和跨间最大弯矩处，下面分别计算各危险截面的抗弯截面系数:

滚圈下支撑处:W1=14.7×105cm3

支撑附近焊缝处:W2=11×105cm3

跨间最大弯矩处:W3=7.7×105cm3

分别计算各危险截面弯曲应力标于弯矩图7中。

括号内为筒体危险截面处的弯曲应力。筒体许用弯曲应力为局部应力允许达到，各危险截面的应力值符合要求［1］。

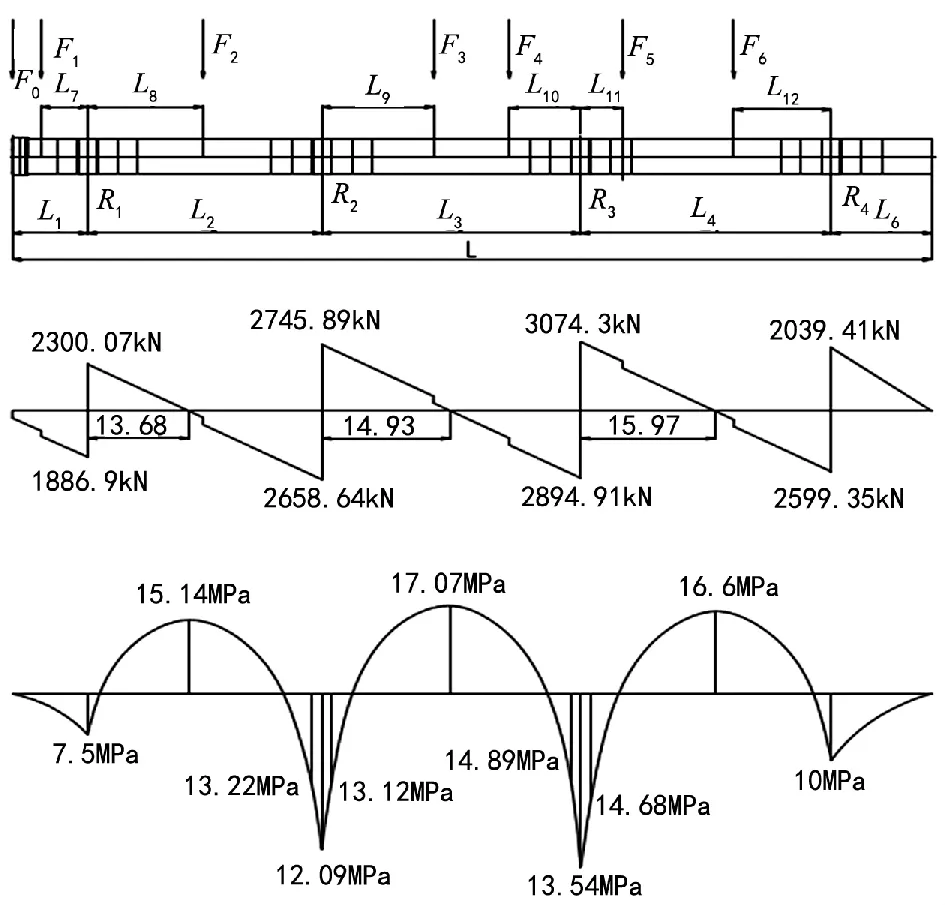
图7 筒体剪力弯矩图

4 结论

本文采用弯矩分配法解决了φ4.8×110 m回转窑筒体设计中，各支撑跨距分配、筒体强度以及各档支撑支反力的计算问题，并为回转窑土建设计以及支撑、传动等设计提供了准确的载荷数据。相比于使用“三弯矩方程”方法，计算量小、步骤清晰、效率高。

［1］ 中国科学院.回转窑(设计、使用与维修)［M］.北京:冶金工业出版社，1978.

［2］ 单辉祖.材料力学［M］.北京:国防工业出版社，1982.

［3］ 中国有色工程设计研究院.机械设计手册［M］.北京:化学工业出版社，2008.