双圆弧齿轮传动模型的建立与动力学接触分析*
2015-06-11朱琳琳武宝林
朱琳琳,武宝林,李 杨
(1.天津工业大学机械工程学院,天津 300387;2.青岛理工大学(临沂)机电工程系,山东临沂 273400)
0 引言
双圆弧齿轮传动具有承载能力高、跑合性能好、润滑良好、加工简单等优点,已广泛应用于我国石油、化工、矿山、冶金等行业[1],缺点是动力性能较差及运行时产生较大噪音,因而限制了其进一步的推广使用,所以对其啮合关系及接触性能研究既有理论意义又有重大的实用价值。
但双圆弧齿轮的接触、跑合过程十分复杂,到目前为止,尚未得到透彻研究,传统双圆弧齿轮的啮合接触分析手段,较为粗糙,不能精确直观的展现双圆弧齿轮的啮合传动过程。ADAMS是集成建模、求解和可视化技术一体的运动仿真软件,是当今世界上应用范围最广的机械系统动力学仿真分析平台之一。它已成功应用于汽车工程、航空航天、铁路车辆、工程机械和工业机械等领域[2]。在精确参数化建成双圆弧齿轮传动模型基础上,使用ADAMS软件仿真更能直观动态描述了双圆弧齿轮啮合接触过程,在双圆弧齿轮啮合传动方面这是一种全新的分析手段。
利用Pro/E对双圆弧齿轮进行参数化建模,将其装配模型导入到ADAMS中建立虚拟样机模型,对模型进行动力学仿真,并对结果进行了分析,为双圆弧齿轮进一步的设计、分析奠定了基础。
1 双圆弧齿轮参数化建模
91型双圆弧齿轮的基本齿廓如图1所示,一个完整的双圆弧齿轮由8段圆弧组成,这些圆弧的位置关系,可以利用各段圆弧圆心坐标、半径及各圆弧起始位置的齿形角来表示。

图1 双圆弧齿轮的基本齿廓
利用接触点做螺旋运动建立齿面方程,如图2所示,以与接触点M面连的坐标系Sn沿着过节On点的螺旋线运动,则形成了圆弧齿轮齿[3]。
经由坐标系Sn-St-S1变换,使坐标轴 x通过齿形对称轴线,再进行如图3所示变换,坐标变换式为:


图2 接触点M面连的坐标系
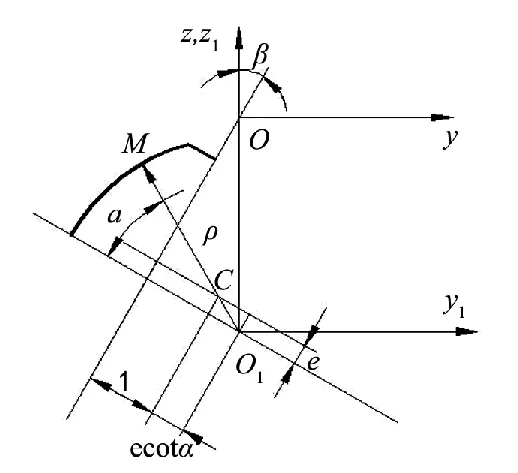
图3 坐标变换
最终经过数学公式的推导得法面圆弧齿轮齿面方程式如式(2):
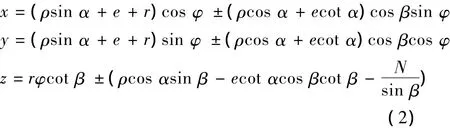
在笛卡尔坐标系中,由齿面方程可以得到一个空间曲面,取方程式z=0得一个平面,则由齿面方程得到的空间曲面和z=0的平面相交,在xoy平面中获得一条曲线,即为端面齿廓。该端面齿廓保持与xoy面平行沿螺旋线方向拉伸同时绕z轴转动角φ(φ满足方程式的约束关系)便得到满足空间方程式的曲面。
将在文本文档中编写的公式导入到Pro/E表达式中,通过Pro/E中特征曲线命令绘制出齿廓曲线和螺旋线,螺旋线方程如式(3):

然后再经过一系列的圆柱拉伸,扫描混合和阵列等命令,建成左右旋两齿轮,以标准中心距装配后得到双圆弧齿轮传动模型[4-5],主要参数如表1所列。

图4 双圆弧齿轮传动模型生成过程

表1 双圆弧齿轮啮合传动模型参数
2 基于ADAMS动力学仿真
2.1 双圆弧齿轮啮合传动系统虚拟样机的建立
启用Pro/E和ADAMS的专用接口模Mechanism-Pro,就可在Pro/E装配环境下直接为装配体加入运动副和力,实现无缝连接,图5为虚拟样机模型。
齿轮材料选择为45钢,小齿轮调质处理,大齿轮正火处理,密度为 ρ=7.801×10-6kg/mm3,弹性模量 E=2.07×105N/mm2,泊松比 μ=0.29。通过分析计算得到双圆弧齿轮传动接触碰撞时的参数如表2所列。

图5 双圆弧齿轮啮合传动虚拟样机模型

表2 双圆弧齿轮传动时的接触碰撞系数
2.2 双圆弧齿轮啮合动力学仿真及结构分析[6-8]
图5所示建立双圆弧齿轮啮合虚拟样机,大小齿轮准确啮合,分别施加旋转副,在齿轮之间添加体-体接触,主动齿轮施加恒定的转速驱动,为了避免由于开始的冲击造成的速度突变,所以转速驱动以阶跃函数施加,由电机功率计算得 STEP(time,0,0d,0.2,1 800 d),在被动齿轮上施加恒定负载转矩921 785 N/mm。轮齿啮合时,存在法向和切向接触力,对样机进行了时间为1 s,步长1 000的动力学仿真,得到如图6~8图所示的结果曲线。

图6 圆周啮合力
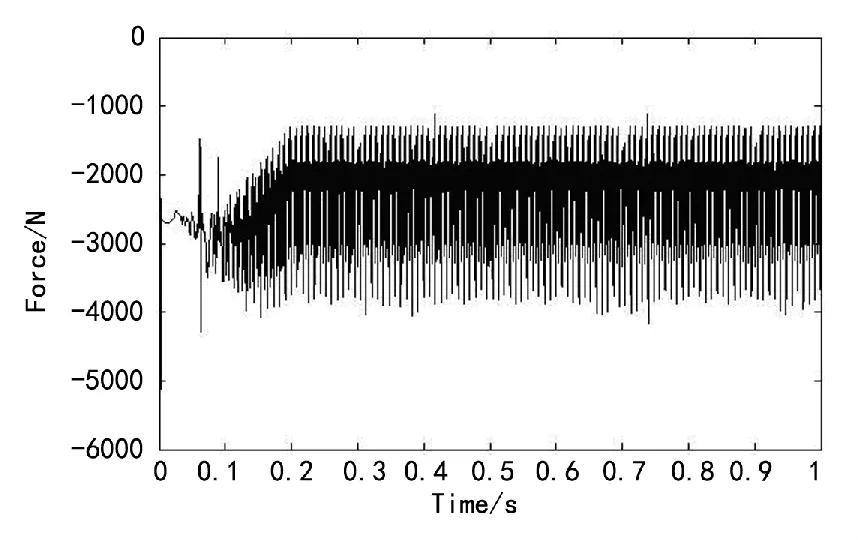
图7 径向啮合力

图8 频谱曲线
从仿真过程分析,在仿真开始的瞬间,突然加速,轮齿啮合力表现出较大的波动,在0~0.2 s内为逐渐加速阶段,波动的幅度较大,波动的周期开始减少。在0.2 s以后,为恒定转速阶段,各个啮合力均在一个均值(传动载荷)附近以一定的幅值上下波动,周期和幅值趋于稳定,这是双圆弧齿轮周期性啮入啮出冲击的体现,将0.2 s后的啮合应力均值与理论计算值进行比较,如表3所列,可见仿真结果较为准确,说明本文虚拟样机模型建立正确,具有较高的可信度。

表3 啮合仿真值与理论计算值的比较
2.3 法向压力角αn对双圆弧啮合传动接触碰撞力的影响
如图9所示在全齿高确定的情况下,法向压力角越大,凸齿廓圆弧半径减小,齿顶变窄齿根变厚。使用Pro/E建模,并进行ADAMS动力学分析得出法向压力角 α 分别为 22°,23°,24°,26°,27°,28°时双圆弧齿轮啮合传动中的接触碰撞力,如表4所列。
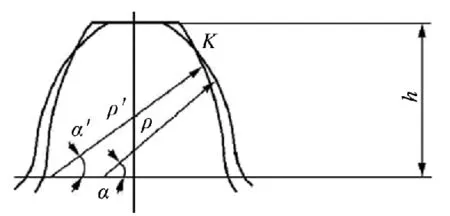
图9 凸齿廓半径ρ与法向压力角α之间的关系
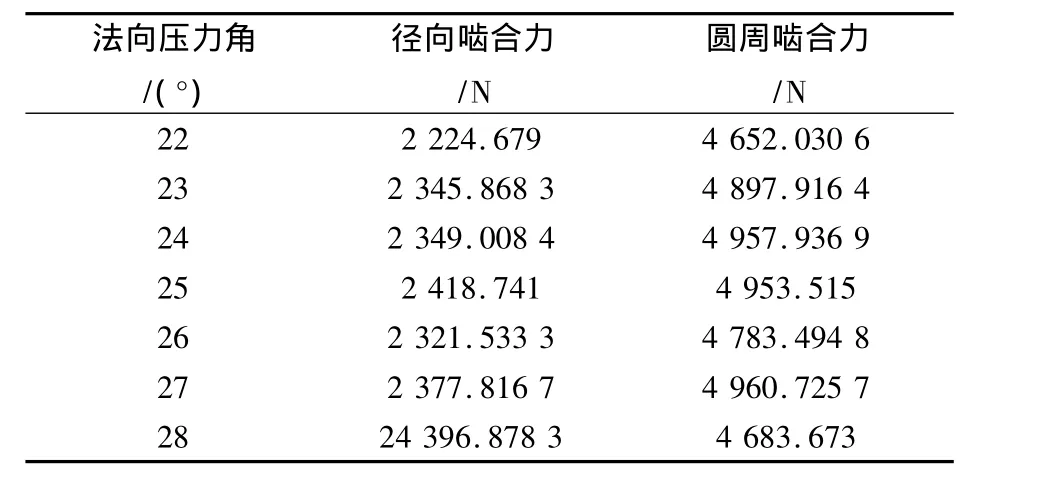
表4 不同法向压力角时,双圆弧齿轮传动的接触碰撞力
由表4数据可知,随着压力角的增大,凹凸齿廓半径增大,齿轮传动中的接触碰撞力层波动性增加趋势。在螺旋角一定的情况下,法向压力角α增大,轮齿传动中径向啮合力增大情况明显,降低了轴承的寿命,综合考虑法向压力角应取23°、24°为宜。
2.4 全齿高h对于双圆弧齿轮啮合传动接触碰撞力的影响
如图10不同齿全高下,双圆弧齿廓有着很大的变化,将直接影响了其啮合传动过程中的弯曲强度和接触强度。同样方法改变双圆弧齿轮的齿全高,进行动力学分析不同齿全高h下的接触碰撞力,如表5。
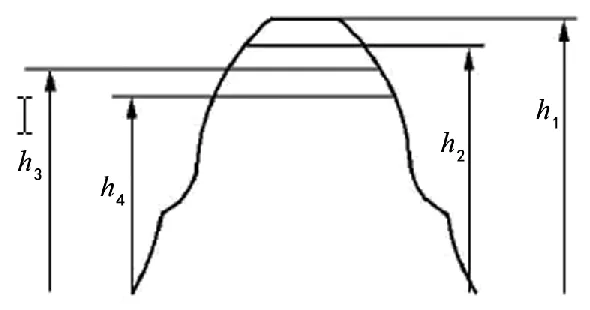
图10 不同全齿高的齿轮轮廓
由表5可看出,随着齿全高的增大,双圆弧齿轮传动的径向啮合力逐渐增大,圆周啮合力的变化情况比较复杂。齿轮材料为钢,根据双圆弧齿轮的实际工况条件,为提高其接触强度,软齿面时全齿高h应取2.0 ~2.2 Mn。
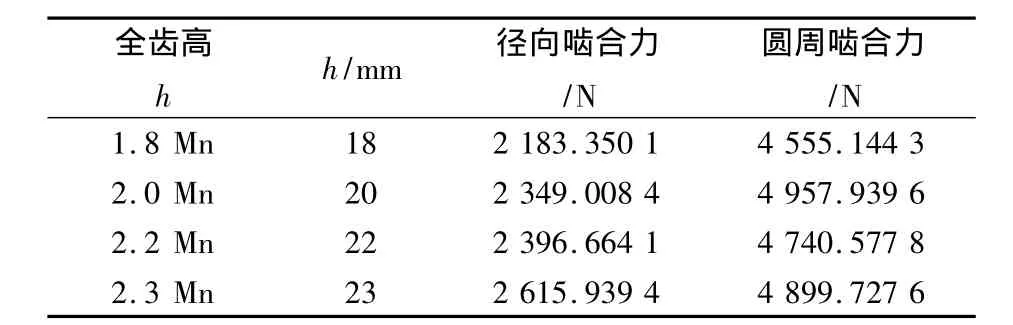
表5 不同齿全高时,双圆弧齿轮传动的接触碰撞力
3 结语
基于Pro/E软件,依据接触点做螺旋运动建立齿面方程,建立了精确的双圆弧齿轮啮合传动模型并对其进行了参数化。通过Pro/E与ADAMS之间的无缝接口程序,实现了在ADAMS环境下双圆弧齿轮啮合传动虚拟样机的创建,并基于接触碰撞算法对齿轮啮合进行了精确的仿真,得到了与理论计算值较吻合的结果,分析法向压力角αn、全齿高h对接触碰撞力的影响,对于双圆弧齿轮的强度校核、优化设计、振动冲击分析等,提供了可靠的依据。
[1] 邵家辉.圆弧齿轮在我国的应用与发展[J].太原工业大学学报,1993(S1):108-112.
[2] 连锦程,崔建昆.基于ADAMS的齿轮传动特性仿真分析[J].制造业自动化,2011(23):148-150.
[3] 卢贤缵,尚俊开.圆弧齿轮啮合原理[M].北京:机械工业出版社,2003.
[4] 王 伟,罗善明,陈立锋,等.基于Pro/E的双圆弧齿轮参数化建模[J].机械设计与制造,2009(2):72-73.
[5] 杨显宏.基于Pro/E双圆弧圆柱齿轮的参数化设计[J].煤矿机械,2012(10):258-259.
[6] 陈峰华.ADAMS2012虚拟样机技术从入门到精通[M].北京:清华大学出版社,2013.
[7] 田会方,林喜镇,赵 恒.基于Pro/E和ADAMS齿轮啮合的动力学仿真[J].机械传动,2006(60:66-69+98.
[8] 王国强,张进平,马若丁.虚拟样机技术及其在ADAMS上的实践[M].西安:西安工业大学出版社,2002.
